Похожие презентации:
Графическое решение уравнений с абсолютной величиной. 8 класс
1. Урок алгебры в 8а классе учитель: Елена Николаевна Кошина МАОУ «СОШ№1»
2. |х|=0,5х+1,5
3. Графическое решение уравнений с абсолютной величиной
Абсолютная величина действительного числа -модульлатинское слово modulus - «мера», «величина». Этот терминввел Роджер Котс (1682-1716) английский математик и
философ, ученик И.Ньютона.
Знак модуля введен в 1841году Карлом Вейерштрассом.
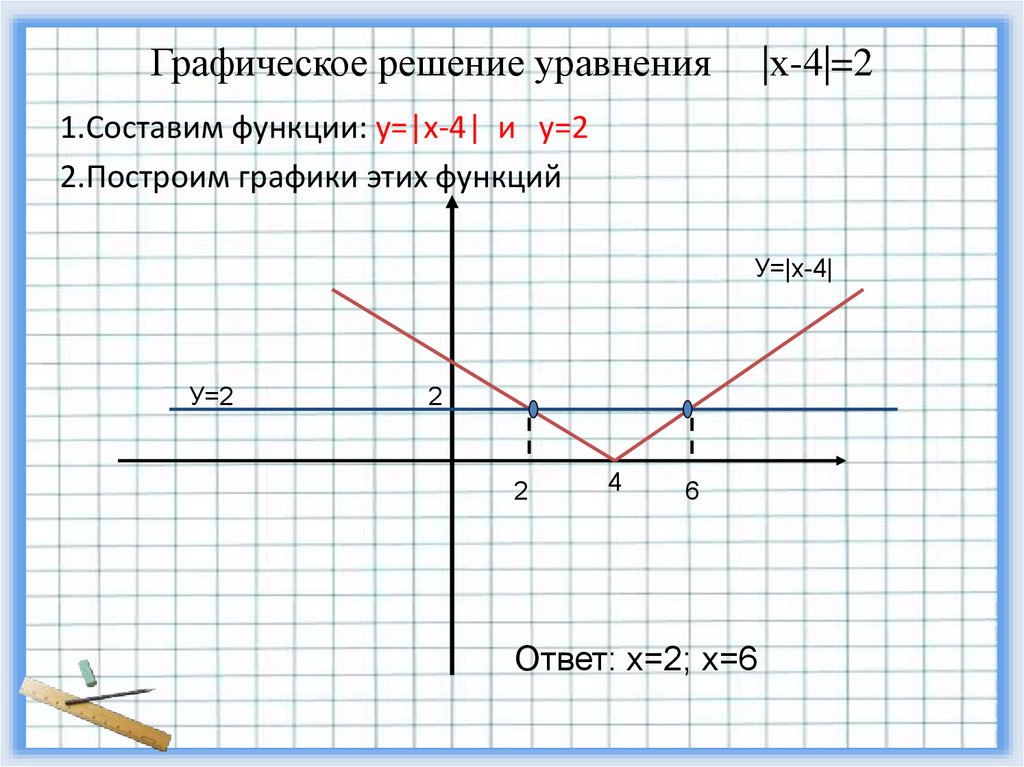
4. Графическое решение уравнения |х-4|=2
1.Составим функции: у=|х-4| и у=22.Построим графики этих функций
У=|х-4|
У=2
2
2
4
6
Ответ: х=2; х=6
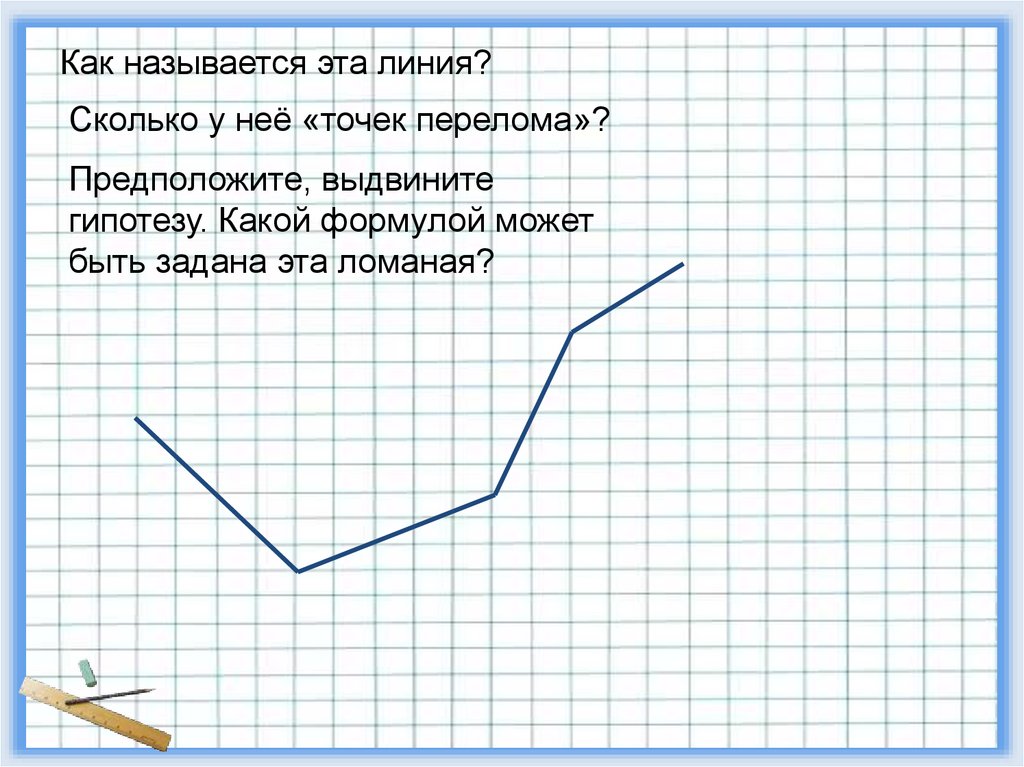
5. Как называется эта линия?
Сколько у неё «точек перелома»?Предположите, выдвините
гипотезу. Какой формулой может
быть задана эта ломаная?
6. 1.Найти «точки перелома»
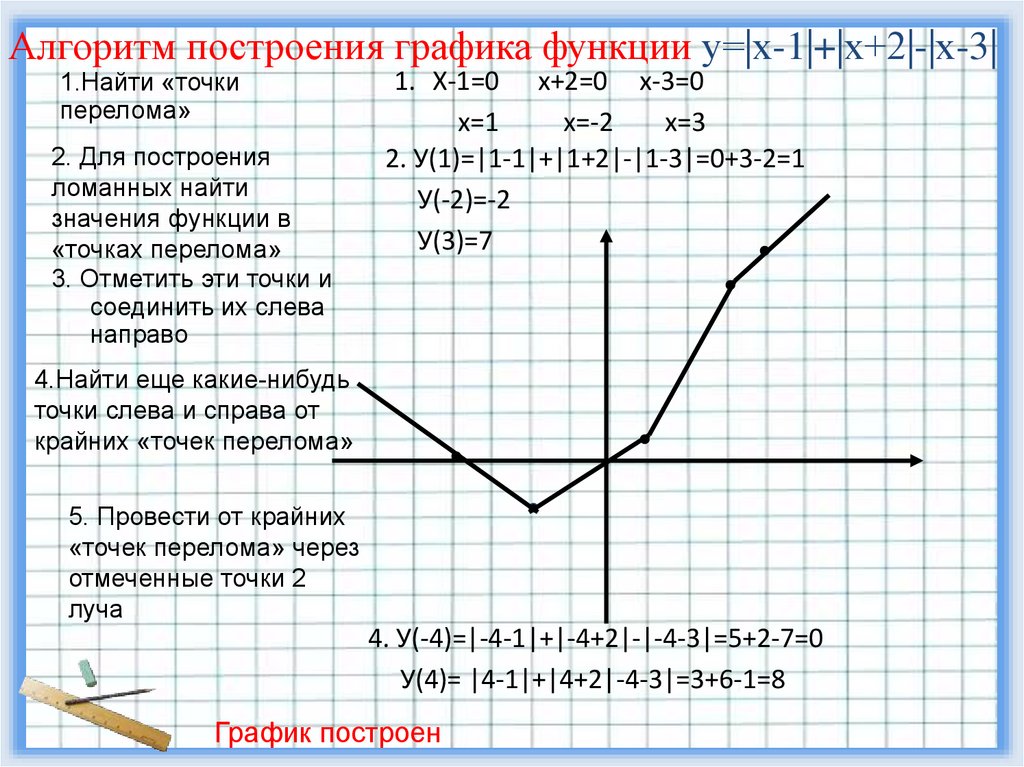
Алгоритм построения графика функции у=|х-1|+|х+2|-|х-3|1.Найти «точки
перелома»
2. Для построения
ломанных найти
значения функции в
«точках перелома»
3. Отметить эти точки и
соединить их cлева
направо
1. Х-1=0 х+2=0 х-3=0
х=1
х=-2
х=3
2. У(1)=|1-1|+|1+2|-|1-3|=0+3-2=1
У(-2)=-2
У(3)=7
4.Найти еще какие-нибудь
точки слева и справа от
крайних «точек перелома»
5. Провести от крайних
«точек перелома» через
отмеченные точки 2
луча
4. У(-4)=|-4-1|+|-4+2|-|-4-3|=5+2-7=0
У(4)= |4-1|+|4+2|-4-3|=3+6-1=8
График построен
7. Решить графическим методом уравнение: |х-1|+|х+2|-|х-3|=1
8. Задание 1: 1вариант |х-1|+|х+2|=|х-3|+1 2вариант |х-1|-1=|х-3|-|х+2|
9. Задание 2: Найдите площадь фигуры, ограниченную линиями, заданные формулами у=|х+1| и у=3-|х|
10. Домашнее задание 1.Найти S фигуры, ограниченную линиями а) у=|х|+|х-2| и у=4 б)у=|х+2|+|х| и у=3 2. Придумать, составить
формулукусочно-линейной функции и
построить график.

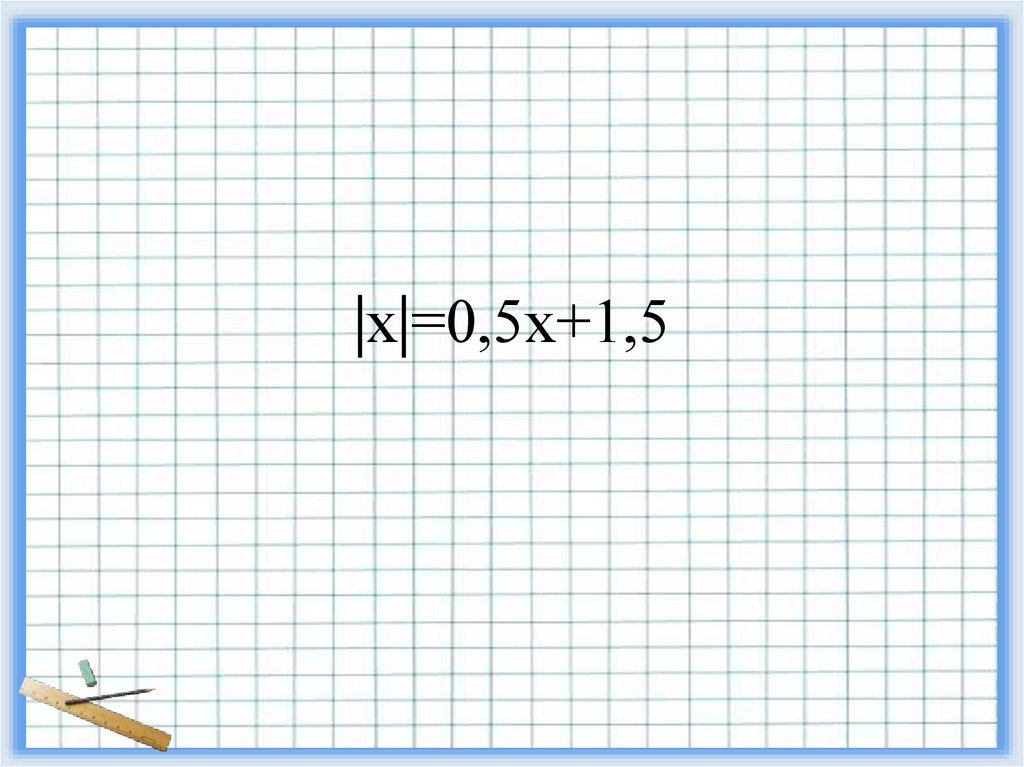





 Математика
Математика








