Похожие презентации:
Методика подготовки обучающихся к решению задачи ЕГЭ по информатике и ИКТ № 27
1.
МЕТОДИКА ПОДГОТОВКИОБУЧАЮЩИХСЯ К РЕШЕНИЮ
ЗАДАЧИ ЕГЭ ПО
ИНФОРМАТИКЕ И ИКТ №27
Учитель информатики
МБОУ «Гимназия №11
им. К.А. Тренева» г. Симферополя
Т.Ю. Буркова
2.
ОСНОВНЫЕ ХАРАКТЕРИСТИКИЗАДАЧИ 27
Уровень сложности – высокий
Время выполнения - 55 минут.
Максимальный первичный балл – 4 балла.
Элементы содержания, проверяемые на ЕГЭ: Основные этапы разработки
программ. Разбиение задачи на подзадачи. Умение создавать собственные
программы (30–50 строк) для решения задач средней сложности
Проверяемые умения или способы действий: Создавать программы на
языке программирования по их описанию
3.
КОДИФИКАТОР ЭЛЕМЕНТОВ СОДЕРЖАНИЯ И ТРЕБОВАНИЙ КУРОВНЮ ПОДГОТОВКИ ВЫПУСКНИКОВ ОБРАЗОВАТЕЛЬНЫХ
ОРГАНИЗАЦИЙ ДЛЯ ПРОВЕДЕНИЯ ЕДИНОГО
ГОСУДАРСТВЕННОГО ЭКЗАМЕНА ПО ИНФОРМАТИКЕ И ИКТ
Возможные алгоритмические задачи для подраздела 1.1 перечня требований к уровню подготовки выпускников,
достижение которых проверяется на едином государственном экзамене по информатике и ИКТ.
− Нахождение минимума и максимума двух, трех, четырех данных чисел без использования массивов и циклов. −
Нахождение всех корней заданного квадратного уравнения.
− Запись натурального числа в позиционной системе с основанием, меньшим или равным 10. Обработка и
преобразование такой записи числа.
− Нахождение сумм, произведений элементов данной конечной числовой последовательности (или массива).
− Использование цикла для решения простых переборных задач (поиск наименьшего простого делителя данного
натурального числа, проверка числа на простоту и т.д.).
− Заполнение элементов одномерного и двумерного массивов по заданным правилам.
− Операции с элементами массива. Линейный поиск элемента. Вставка и удаление элементов в массиве. Перестановка
элементов данного массива в обратном порядке. Суммирование элементов массива. Проверка соответствия элементов
массива некоторому условию.
− Нахождение второго по величине (второго максимального или второго минимального) значения в данном массиве за
однократный просмотр массива.
− Нахождение минимального (максимального) значения в данном массиве и количества элементов, равных ему, за
однократный просмотр массива.
− Операции с элементами массива, отобранных по некоторому условию (например, нахождение минимального четного
элемента в массиве, нахождение количества и суммы всех четных элементов в массиве).
− Сортировка массива. − Слияние двух упорядоченных массивов в один без использования сортировки.
− Обработка отдельных символов данной строки. Подсчет частоты появления символа в строке.
− Работа с подстроками данной строки с разбиением на слова по пробельным символам. Поиск подстроки внутри данной
строки, замена найденной подстроки на другую строку.
4.
ЗАДАЧА А• Максимальный балл
– 2 балла
• Решение может быть
неэффективным по
времени и по памяти
• Может быть указано
исходное количество
обрабатываемых
значений
ЗАДАЧА Б
• Максимальный балл
• – 4 балла
• Решение должно быть
эффективным
по времени и
по памяти
5.
ЭФФЕКТИВНОСТЬ ПО ВРЕМЕНИВремя работы программы пропорционально количеству
входных данных, т.е. при увеличении N в k раз время работы
программы должно увеличиваться не более чем в k раз.
6.
ЭФФЕКТИВНОСТЬ ПО ПАМЯТИ• Не используются массивы и другие структуры данных,
размер которых зависит от количества входных
элементов
7.
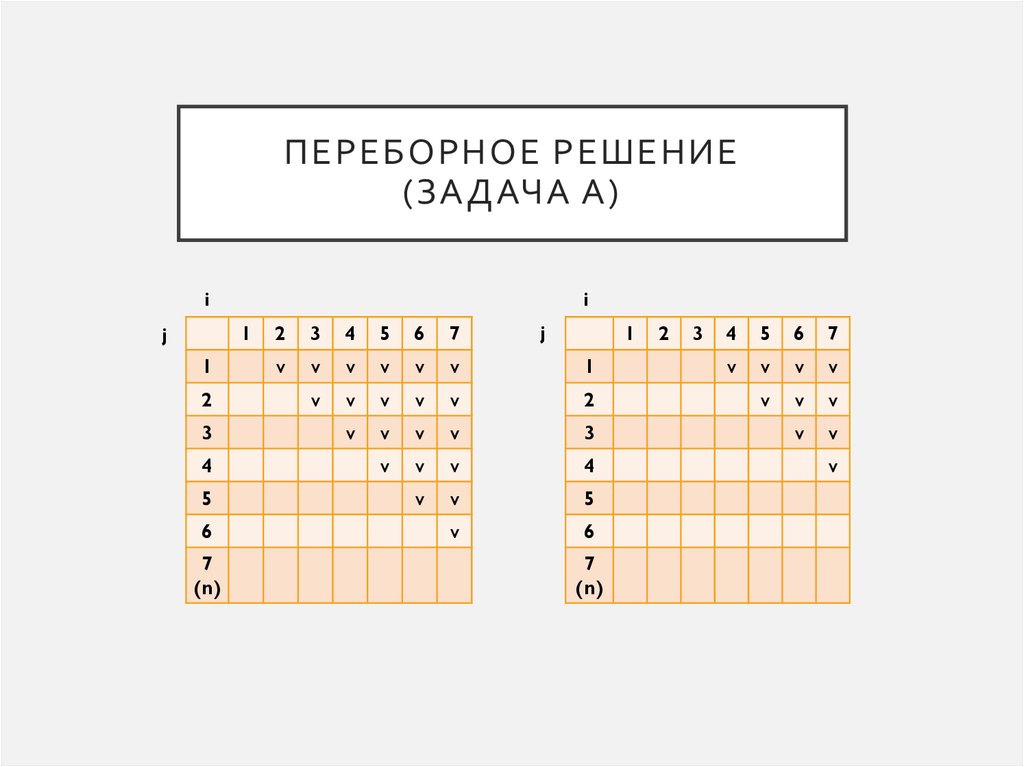
ПЕРЕБОРНОЕ РЕШЕНИЕ(ЗАДАЧА А)
i
i
1
j
1
2
3
4
5
6
7
(n)
j
2
3
4
5
6
7
1
v
v
v
v
v
v
1
v
v
v
v
v
2
v
v
v
v
3
v
v
v
4
v
v
5
v
6
7
(n)
2
3
4
5
6
7
v
v
v
v
v
v
v
v
v
v
8.
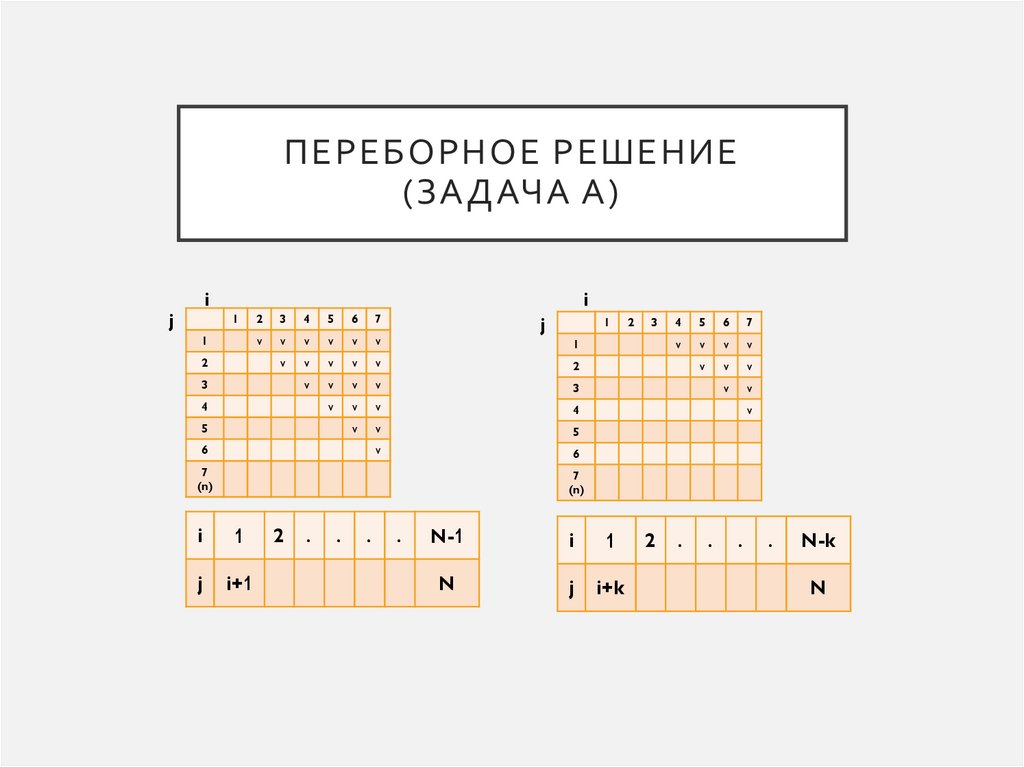
ПЕРЕБОРНОЕ РЕШЕНИЕ(ЗАДАЧА А)
i
j
i
1
1
2
2
3
4
5
6
7
v
v
v
v
v
v
v
v
v
v
v
2
v
v
v
v
3
v
v
v
4
v
v
5
v
6
3
4
5
6
j
1
2
3
1
7
(n)
4
5
6
7
v
v
v
v
v
v
v
v
v
v
7
(n)
i
1
j
i+1
2
.
.
.
.
N-1
i
1
N
j
i+k
2
.
.
.
.
N-k
N
9.
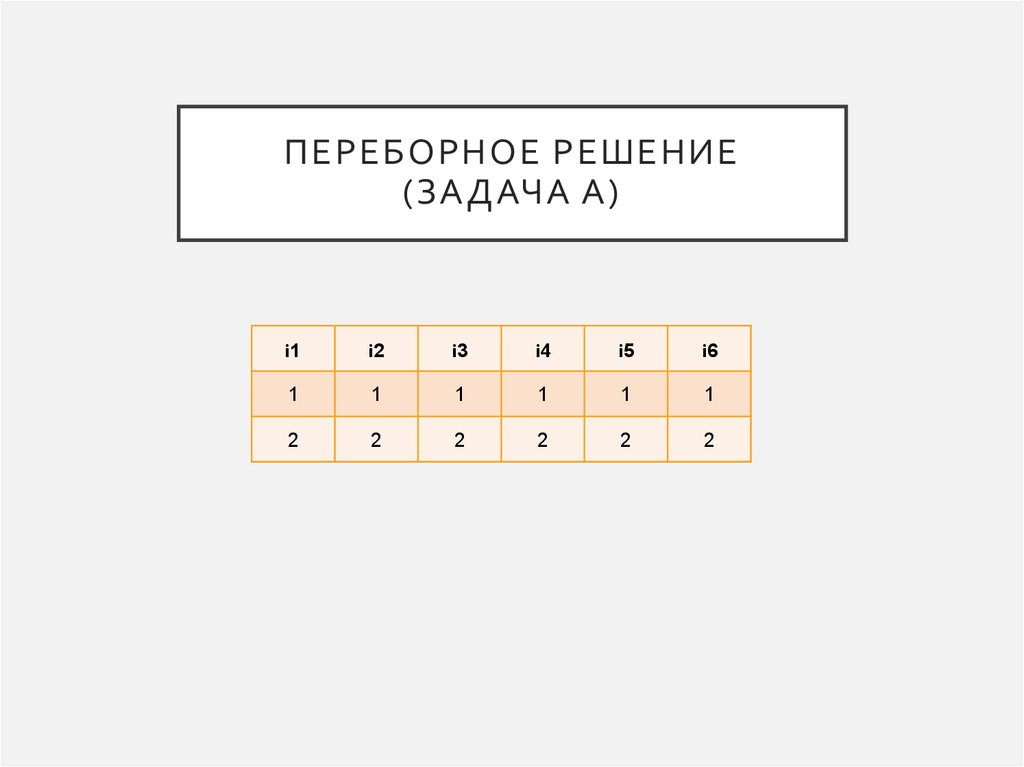
ПЕРЕБОРНОЕ РЕШЕНИЕ(ЗАДАЧА А)
i1
i2
i3
i4
i5
i6
1
1
1
1
1
1
2
2
2
2
2
2
10.
НА ЧТО ОБРАТИТЬ ВНИМАНИЕ• Параметры изменения счетчиков
• Инициализация счетчиков, переменных для поиска
максимальных и минимальных значений
• Вывод результата
• Типы данных
• Оформление решения
• Пояснение
11.
• Компьютер наземной станции слежения получает от объектов –самолетов, находящихся в зоне ее работы, идентификационные
сигналы, представляющие собой последовательность из N целых
положительных чисел. Каждый объект направляет на наземную
станцию уникальное число, т.е. все числа в получаемой станцией
последовательности различны. Обработка сигнала представляет собой
рассмотрение всех пар различных элементов последовательности, при
этом элементы пары не обязаны быть переданы непосредственно друг
за другом, порядок элементов в паре не важен. Считается, что возникла
критическая ситуация, если произведение элементов некоторой пары
кратно 58. Необходимо определить общее количество возникших
критических ситуаций.
• Описание входных и выходных данных.
• В первой строке входных данных задается количество чисел N (1<= N
<= 1000). В каждой из последующих N строк записано одно целое
положительное число, не превышающее 10 000.
• В качестве результата программа должна напечатать одно число:
общее количество возникших критических ситуаций.
12.
КОГДА ПРОИЗВЕДЕНИЕ ДВУХЧИСЕЛ ДЕЛИТСЯ НА 58?
Когда оба
сомножителя
делятся на 58.
n58*(n58-1)/2
Только один
сомножитель
делится на 58.
n58*(N-n58)
Одно число
делится на 2,
другое на 29.
n2*n29
13.
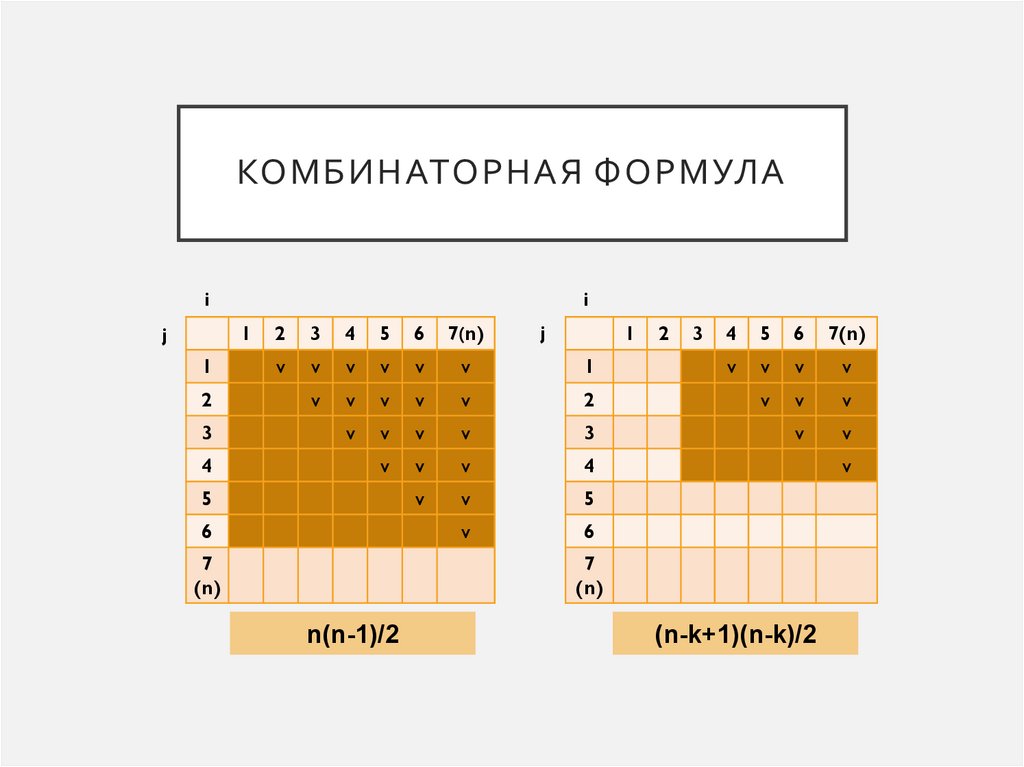
КОМБИНАТОРНАЯ ФОРМУЛАi
i
1
j
1
2
3
4
j
2
3
4
5
6
7(n)
v
v
v
v
v
v
1
v
v
v
v
v
2
v
v
v
v
3
v
v
v
4
v
v
5
v
6
5
6
7
(n)
1
2
3
4
5
6
7(n)
v
v
v
v
v
v
v
v
v
v
7
(n)
n(n-1)/2
(n-k+1)(n-k)/2
14.
n58 = 0n29 = 0
n2 = 0
N = int(input())
for i in range(N):
temp= int(input())
if temp%58 == 0:
n58++
elif temp%29 ==0:
n29++
elif temp%2 == 0:
n2++
crypt = (n58*(n58-1))/2 + n58*(N-n58) +n29*n2
print(crypt)
15.
16.
var a: array [1..5] of integer;kp, k13, kn13, i, n, b: integer;
begin
kp:=0;
k13:=0;
kn13:=0;
for i:=1 to 5 do readln( a[i]);
for i:=6 to n do
begin
if a[i mod 5] mod 13=0
then k13:= k13 + 1
else kn13 :=kn13 + 1;
readln (b);
if b mod 13 <>0
then kp:= kp + k13
else kp := kp + k13 + kn13;
a[i mod 5] :=b;
end;
writeln (kp);
end.
17.
• Датчик передает каждую секунду по каналу связи неотрицательноецелое число, не превосходящее 1000, - текущий результат измерений.
Временем, в течение которого происходит передача, можно
пренебречь.
• Необходимо найти в заданной серии показаний датчика минимальное
четное произведение двух показаний, между моментами передачи
которых прошло не менее 15 секунд. Если получить такое произведение
не удается, ответ считается равным -1. Общее количество показаний
датчика в серии не превышает 10 000.
• А. Напишите программу, в которой входные данные будут запоминаться
в массиве, после чего будут проверены все возможные пары элементов.
• Б. Напишите программу, которая будет эффективной по времени и по
памяти.
18.
#include <iostream>#include <queue>
using namespace std;
int main(){
queue <int> mas;
int N, a;
long int min, min_out15_even, minn_out15, temp;
cin >> N;
for (int i=0; i<15; i++){
cin >> a;
mas.push(a);
}
min = -1;
min_out15_even = 0;
min_out15 = 0;
for (i=0; i<N-15; i++){
a = mas.pop();
if ((a%2==0)&&(min_out15_even==0 || a<min_out15_even)) min_out15_even = a;
if (min_out15==0 || a<min_out15) min_out15 = a;
cin >> a;
mas.push(a);
if (a%2==0) temp=min_out15*a;
else temp=min_out15_even*a;
if (min==-1 || min>temp) min = temp;
}
cout << min <<endl;
}
19.
• А. Имеется набор данных, состоящий из 6 парположительных целых чисел. Необходимо выбрать из
каждой пары одно число так, чтобы сумма всех выбранных
чисел не делилась на 5 и при этом была максимально
возможной. Если получить требуемую сумму невозможно, в
качестве ответа нужно выдать 0.
• Б. Имеется набор данных, состоящий из пар положительных
целых чисел. Необходимо выбрать из каждой пары одно
число так, чтобы сумма всех выбранных чисел не делилась на
5 и при этом была максимально возможной. Если получить
требуемую сумму невозможно, в качестве ответа нужно
выдать 0.
20.
#include <iostream>using namespace std;
int main(){
int max, max_t, min_t, min_d, temp;
int N;
max = 0;
min_d = 0;
cin >> N;
for (int i=0;i<N;i++){
cin >> max_t >> min_t;
if (min_t > max_t){
temp = max_t;
max_t = min_t;
main_t = temp;
}
max += max_t;
temp = max_t – min_t;
if (temp%5 != 0){
if (min_d == 0 || min_d > temp) min_d = temp;
}
}
If (max %5 != 0) cout << max << endl;
else if (min_d >0){
max -= min_d;
cout << max << endl;
} else cout << 0 << endl;
}
















 Программирование
Программирование








