Вписанный и описанный около призмы цилиндр

1.

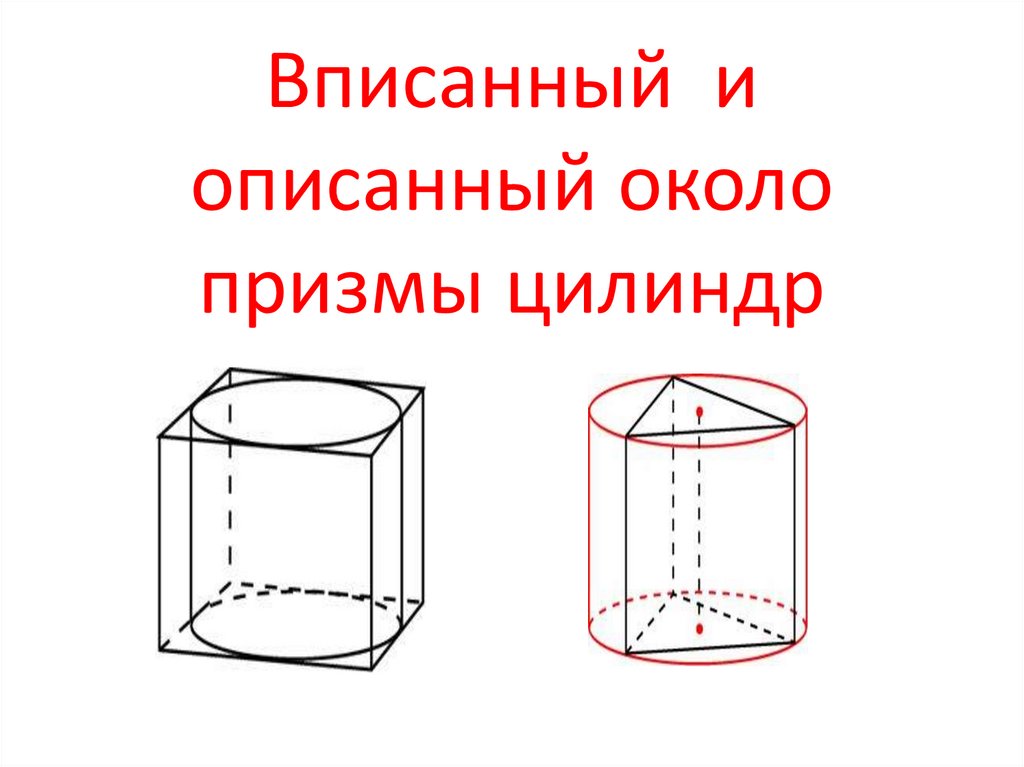
Вписанный и
описанный около
призмы цилиндр

2.

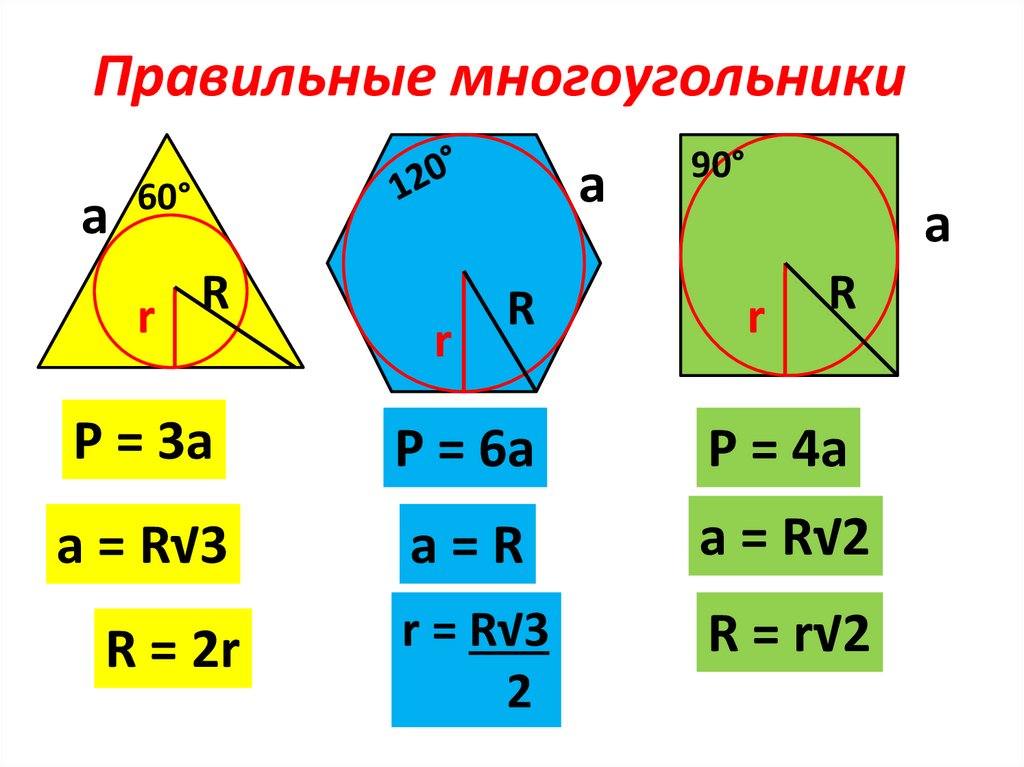
Правильные многоугольники
a
a
60°
R
r
r
R
90°
a
r
R
P = 3a
P = 6a
P = 4a
a = R√3
a=R
a = R√2
r = R√3
2
R = r√2
R = 2r

3.

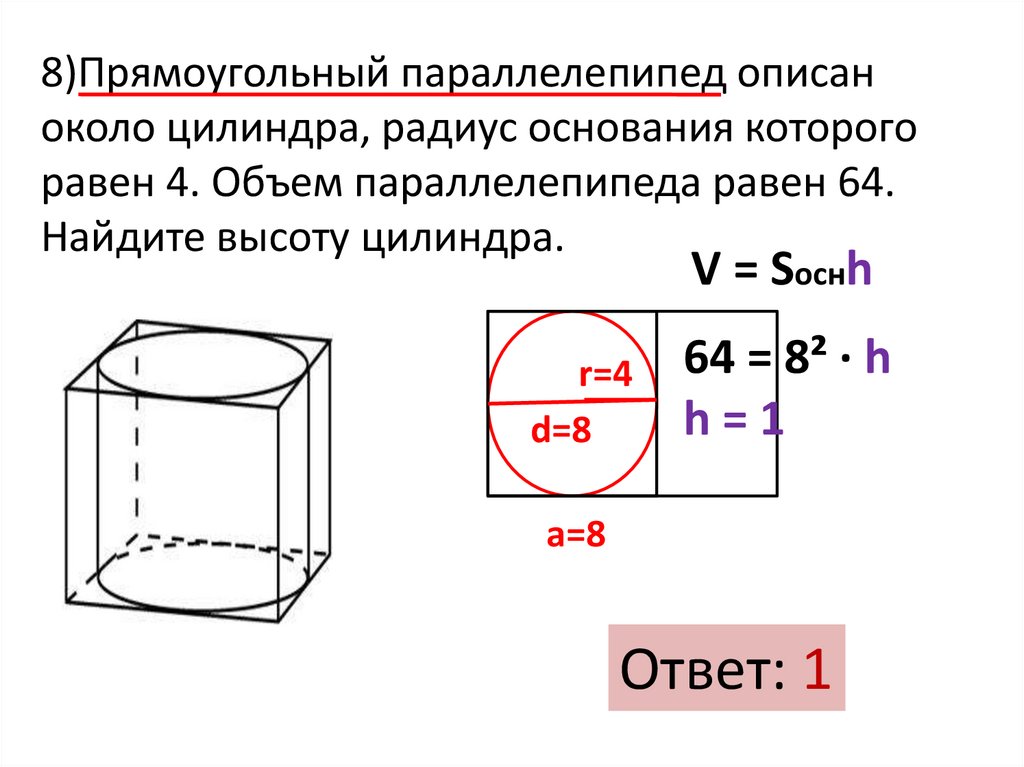
8)Прямоугольный параллелепипед описан
около цилиндра, радиус основания которого
равен 4. Объем параллелепипеда равен 64.
Найдите высоту цилиндра.
V = Sоснh
r=4
d=8
64 = 8² ∙ h
h=1
a=8
Ответ: 1

4.

9)Найдите площадь боковой поверхности
правильной треугольной призмы,
описанной около цилиндра, радиус основания
которого равен √3, а высота равна 2.
r=√3
R=2√3
Sбок. = Pосн.h
Sбок. = (6∙3) ∙2 = 18
a=R√3 = 2√3∙ √3=6
Ответ: 36

5.

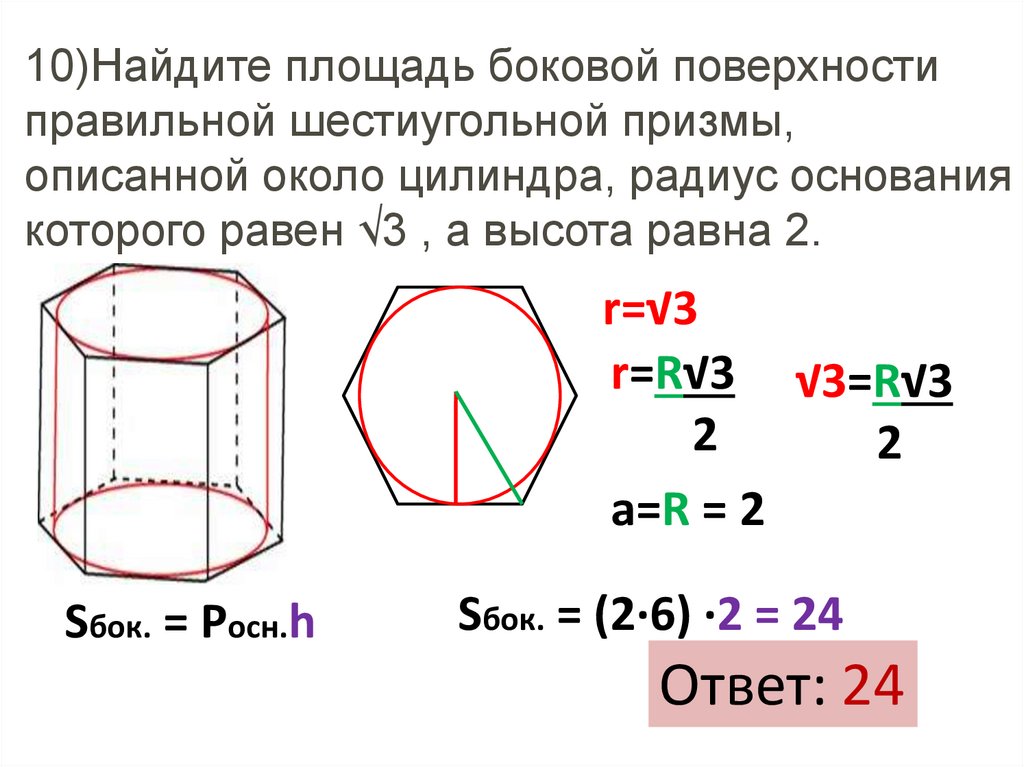
10)Найдите площадь боковой поверхности
правильной шестиугольной призмы,
описанной около цилиндра, радиус основания
которого равен √3 , а высота равна 2.
r=√3
r=R√3 √3=R√3
2
2
a=R = 2
Sбок. = Pосн.h
Sбок. = (2∙6) ∙2 = 24
Ответ: 24

6.

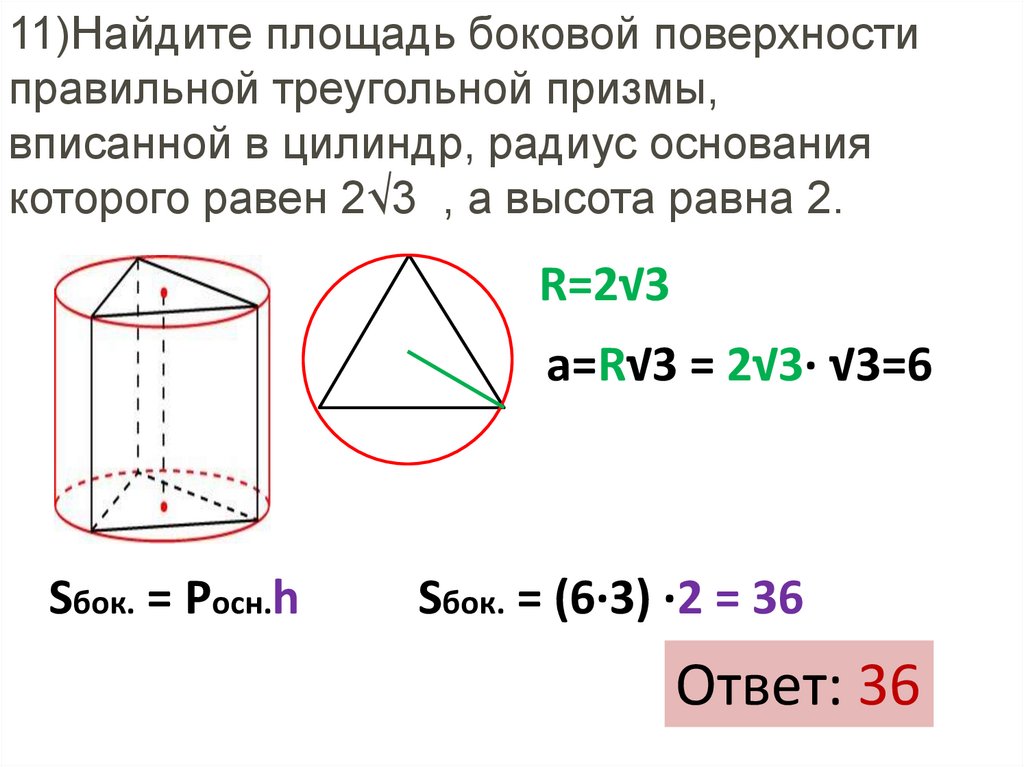
11)Найдите площадь боковой поверхности
правильной треугольной призмы,
вписанной в цилиндр, радиус основания
которого равен 2√3 , а высота равна 2.
R=2√3
a=R√3 = 2√3∙ √3=6
Sбок. = Pосн.h
Sбок. = (6∙3) ∙2 = 36
Ответ: 36

7.

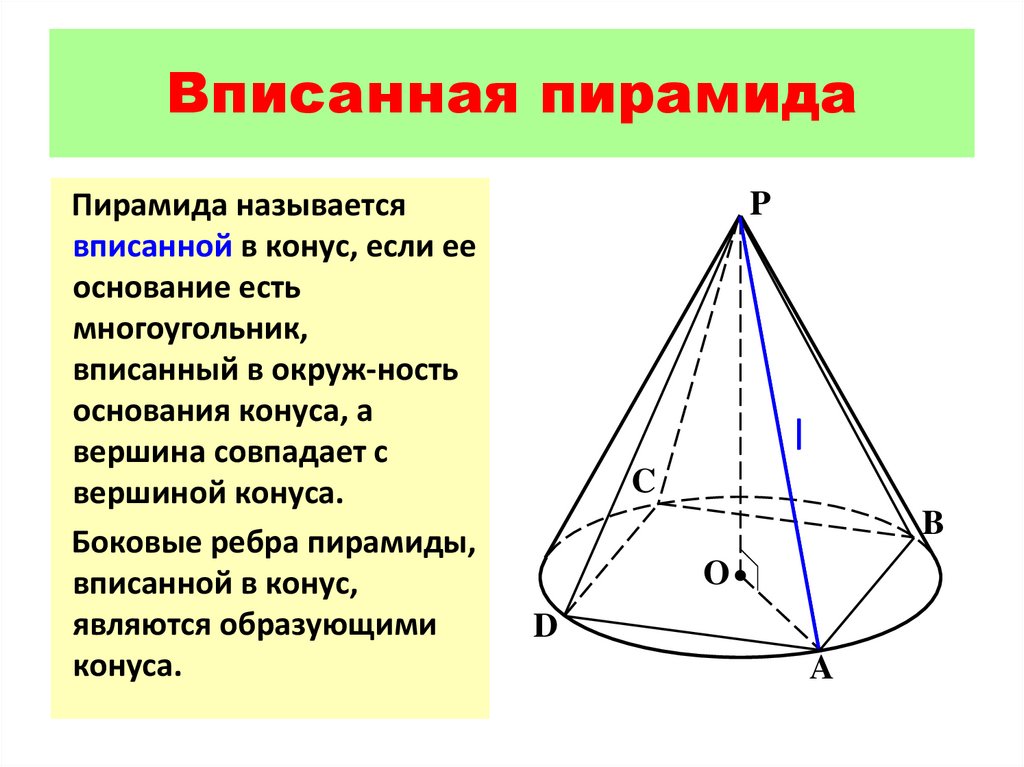
Вписанная пирамида
Пирамида называется
вписанной в конус, если ее
основание есть
многоугольник,
вписанный в окруж-ность
основания конуса, а
вершина совпадает с
вершиной конуса.
Боковые ребра пирамиды,
вписанной в конус,
являются образующими
конуса.
P
l
C
B
O
D
A

8.

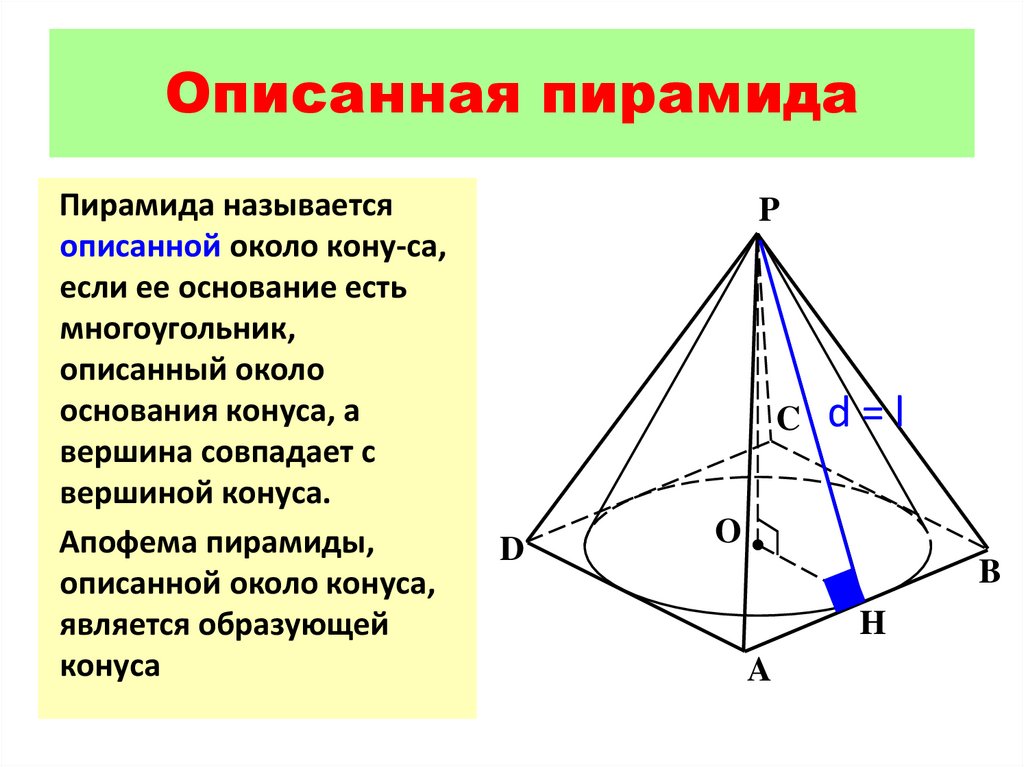
Описанная пирамида
Пирамида называется
описанной около кону-са,
если ее основание есть
многоугольник,
описанный около
основания конуса, а
вершина совпадает с
вершиной конуса.
Апофема пирамиды,
описанной около конуса,
является образующей
конуса
P
C
D
d=l
O
B
H
A

9.

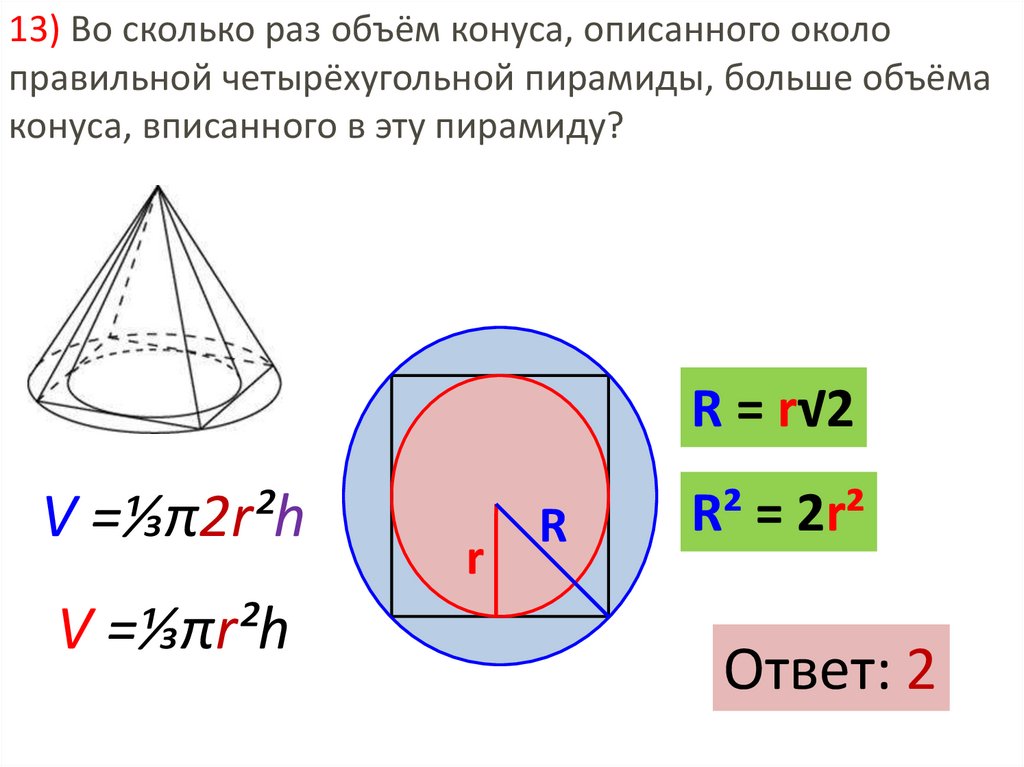
13) Во сколько раз объём конуса, описанного около
правильной четырёхугольной пирамиды, больше объёма
конуса, вписанного в эту пирамиду?
R = r√2
V =⅓π2r²h
V =⅓πr²h
r
R
R² = 2r²
Ответ: 2

10.

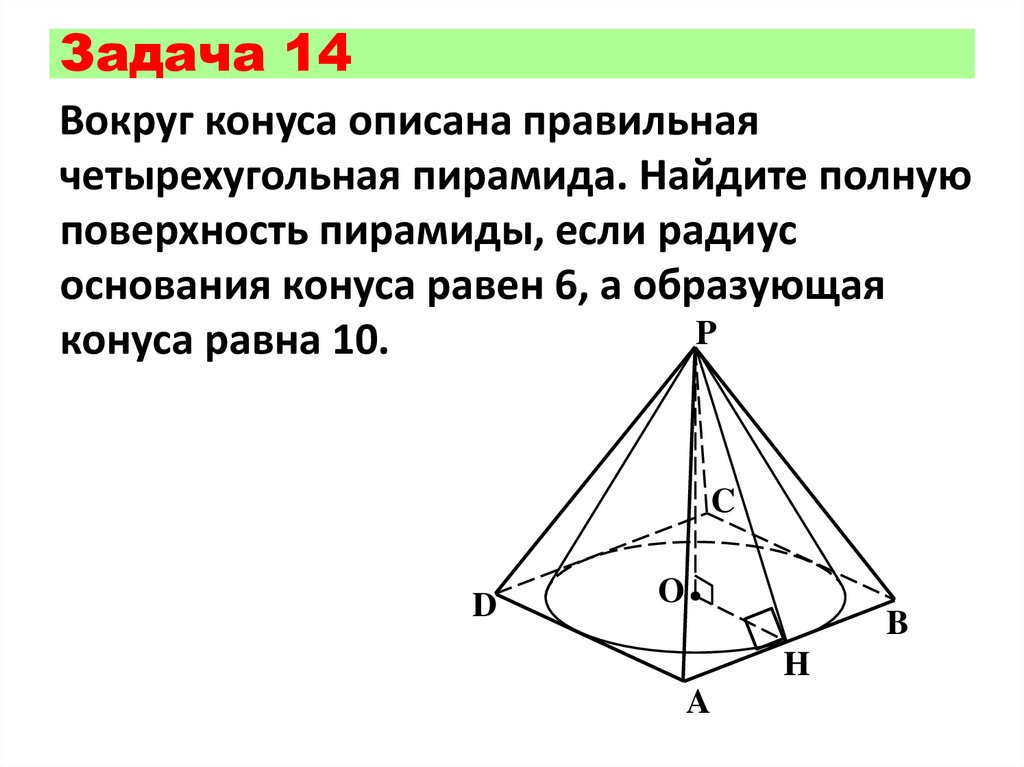
Задача 14
Вокруг конуса описана правильная
четырехугольная пирамида. Найдите полную
поверхность пирамиды, если радиус
основания конуса равен 6, а образующая
P
конуса равна 10.
C
D
O
B
H
A

11.

Задача 14.
S бок = 0,5 Росн d = 0,5∙(4∙12)∙10 = 240
P
S осн = 12² = 144
S полн. -?
C
8
B
C 10
O
D
6
O
H
B
6
H
A
S полн = 144 + 240 = 384
D
12
A
Ответ: 384

12.

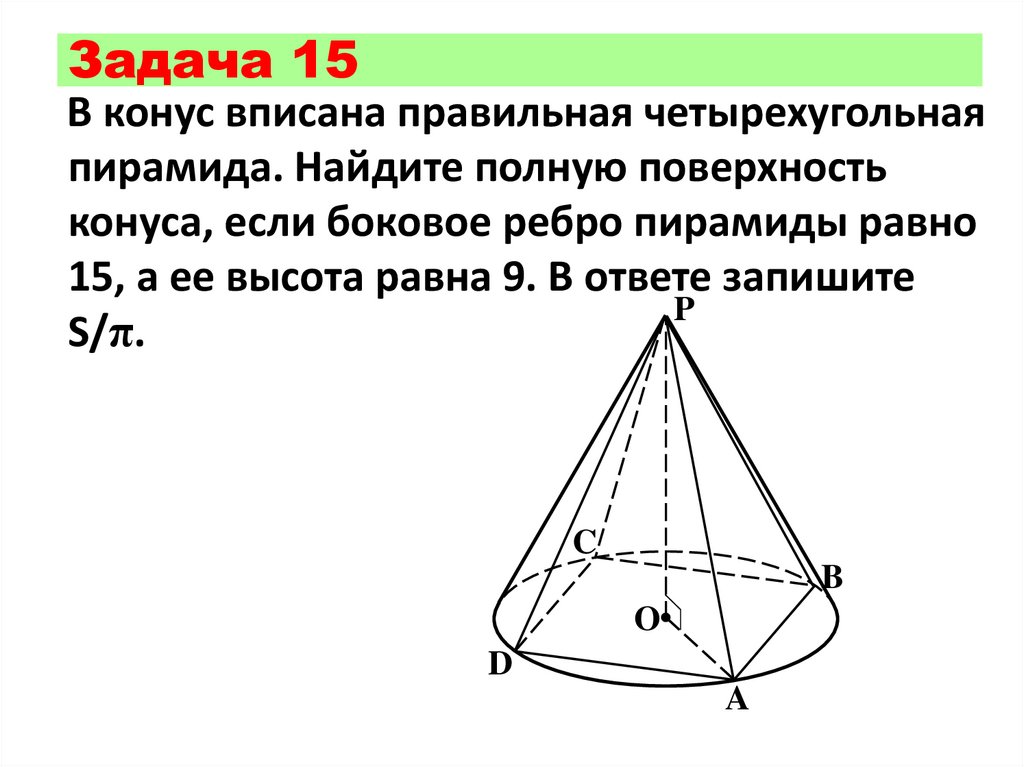
Задача 15
В конус вписана правильная четырехугольная
пирамида. Найдите полную поверхность
конуса, если боковое ребро пирамиды равно
15, а ее высота равна 9. В ответе запишите
P
S/π.
C
B
O
D
A

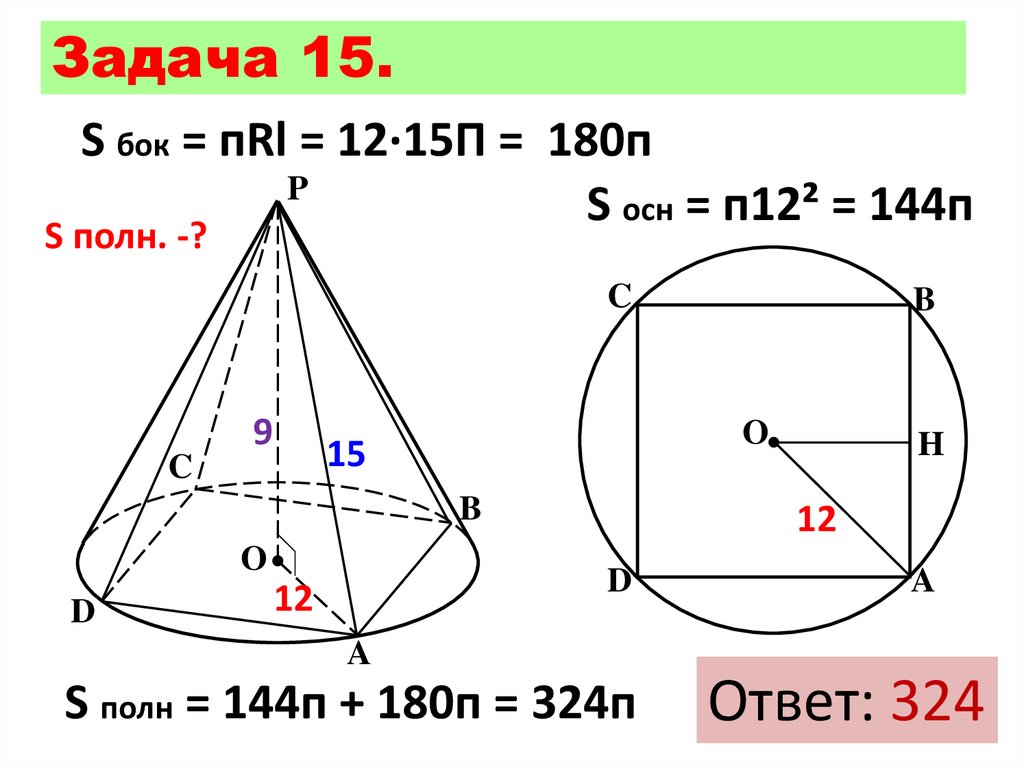
13.

Задача 15.
S бок = пRl = 12∙15П = 180п
P
S осн = п12² = 144п
S полн. -?
C
9
O
15
C
B
O
D
H
12
D
12
B
A
A
S полн = 144п + 180п = 324п
Ответ: 324