Перпендикулярность прямых, прямой и плоскости

1.

Университетский лицей №1523
Предуниверситария НИЯУ МИФИ
Лекции по геометрии
10 класс
© Хомутова Лариса Юрьевна
© Крайко Мария Александровна

2.

Перпендикулярность прямых,
перпендикулярность
прямой и плоскости
в пространстве.

3.

1. Перпендикулярность прямых.
Две прямые в пространстве называются перпендикулярными,
если угол между ними равен 90 .
В пространстве перпендикулярные прямые могут быть как
пересекающимися, так и скрещивающимися.
К примеру, CC1 A1D1 и CC1 B1C1, т.к.
(CC1, A1D1) = (CC1; B1C1) = 90 .

4.

.
Лемма. Если одна из двух
перпендикулярна третьей прямой,
перпендикулярна ей.
параллельных прямых
то и вторая прямая
Обратный факт неверен: две прямые, перпендикулярные третьей
прямой, могут быть как пересекающимися или параллельными,
так и скрещивающимися.
К примеру, на рисунке
C1D1 CC1 A1D1, и при этом C1D1 A1D1,
C1D1 CC1 CD, и при этом C1D1 CD,
A1D1 CC1 CD, и при этом A1 D1 CD

5.

2. Перпендикулярность прямой и плоскости.
Прямую называют перпендикулярной плоскости, если она
перпендикулярна каждой прямой, лежащей в этой плоскости:
a l , a l
Теорема о существовании и единственности прямой перпендикулярной плоскости:
Через данную точку можно провести прямую, перпендикулярную данной плоскости, и
притом только одну.

6.

Теорема. Свойство параллельных прямых, перпендикулярных плоскости:
Если одна из двух параллельных прямых перпендикулярна плоскости, то и
вторая прямая перпендикулярна этой же плоскости.
Доказательство:
Возьмем в плоскости произвольную прямую l и докажем,
что b l:
a ,
Т.к.
a l; а т.к. b a l, b l.
l
,
Итак, прямая b перпендикулярна всякой прямой, лежащей в плоскости , а
значит, b .

7.

Справедлива и обратная теорема –
признак параллельности прямых, перпендикулярных плоскости:
Две прямые, перпендикулярные одной и той же плоскости, параллельны.
Доказательство:
1) Допустим, что a b. Возьмем на
прямой b произвольную точку B и
проведем через нее прямую b a .
Тогда по свойству параллельных прямых,
перпендикулярных плоскости, b .
Пусть b = Q, b = P.
По определению перпендикулярности
прямой и плоскости, b ,
PQ ,
b PQ.
Аналогично b PQ, а значит, в треугольнике BPQ есть два прямых угла, что
невозможно. Следовательно, предположение неверно, т.е. a b.

8.

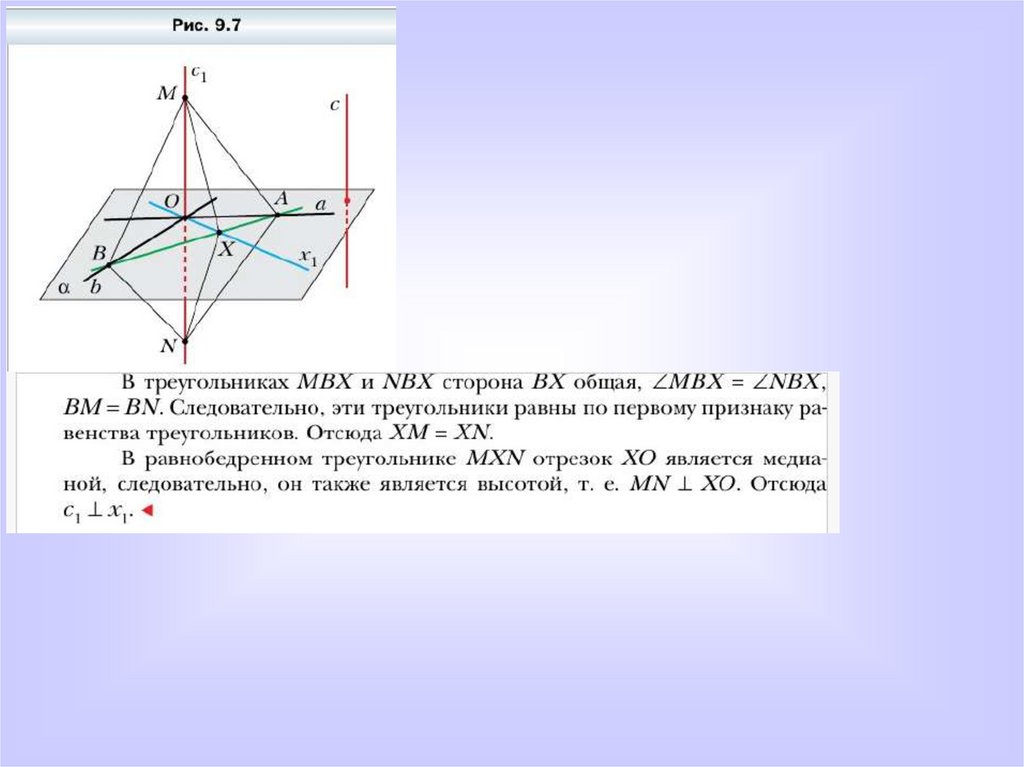
Теорема. Признак перпендикулярности прямой и плоскости:
Если прямая перпендикулярна двум пересекающимся прямым, лежащим в плоскости,
то она перпендикулярна самой плоскости.

9.

10.

11.

Ключевая задача:
Доказать, что скрещивающиеся ребра правильной треугольной пирамиды
перпендикулярны.
Доказательство:
1. Пусть M – середина ребра BC .
Тогда по свойству медианы равнобедренного
треугольника, DM BC, AM BC.