«Основы теории надежности» для специализаций ЭНС,АТ,ТС

1.

Слайд-шоу по дисциплине
«Основы теории надежности»
для специализаций ЭНС,АТ,ТС
Автор к.т.н., профессор Харченко А.Ф.

2. Рекомендованная литература

Острейковский В.А. Теория надежности. Учебник для
вузов. – М.: Высшая школа 2008.
Надежность систем железнодорожной автоматики,
телемеханики и связи. Под ред. Вл.В Сапожникова.
Учеб. пособие.- М.: Маршрут, 2003.
Половко А.М., Гуров С.В. Основы теории надежности.
-СПб,: БХВ-Петербург, 2008.
Харченко А.Ф. Основы теории надежности
устройств электроснабжения. Учеб. пособие.- М.:
МИИТ, 2010.
Горелик А.В., Ермакова О.П. Основы теории
надежности в примерах и задачах. Учеб. пособие.
Гмурман В.Е.. Теория вероятностей и математическая
статистика- М.: Высшая школа, 2002.
Лекции -8 ч; Практические занятия – 8 ч; КР; КСР, Экз.

3. Надежность является одним из самых важных показателей современной техники. От неё зависят такие показатели, как качество, эффективность, б

Надежность является одним из самых важных
показателей современной техники. От неё зависят
такие показатели, как качество, эффективность,
безопасность, риск, готовность.
При этом эти показатели получают количественные
значения.
Цель изучения дисциплины «Основы теории надежности»
- формирование у
студентов
знаний и умений
использовать современные методы подходов к
обеспечению условий
надежного функционирования
технических
устройств
ЭНС,АТ,ТС
на
этапах
конструирования
(проектирования)
изготовления,
испытания, технического обслуживания и ремонта.
Эти методы реализованы на базе основ теории
надежности и ее знание необходимо широкому кругу
специалистов.

4. Введение

Технические средства применяемые в устройствах
электроснабжения, автоматики, телемеханики и
связи имеют свою специфику, но
все эти
технические системы объединяет то, что в них в
основном
применяются
электротехнические
элементы и элементы радиоэлектроники.
Проблема надежности этих элементов стала
занимать центральное место
в связи с все
большей сложностью технических объектов и
систем, а так же большим количеством факторов,
влияющих
на
надежность
элементов
электроустановок.

5.

Эти факторы можно подразделить на четыре группы:
• Воздействия окружающей среды интенсивность
грозовой
и
ветровой
деятельности,
изменение
температуры, мокрый снег, густой туман, роса, изморозь,
солнечная радиация.
•Эксплуатационныеперегрузки
элементов
электроустановок,
неудовлетворительное
состояние
защиты от внутренних и
грозовых перенапряжений,
квалификация персонала и сопутствующие этому
воздействия (ошибки персонала, некачественный ремонт
и обслуживание и т.п.).
•Ошибки
конструирования
(проектирования),
изготовления и монтажа - сводятся к несоблюдению
требований руководящих или нормативных документов и
неучет требований надежности.
•Случайные -наезд транспорта, обрыв проводов,
вандализм, повреждение животными.

6. Область применения теории надежности ограничена крупносерийными объектами, которые изготавливаются и эксплуатируются в статистически о

Область применения теории надежности ограничена
крупносерийными объектами, которые изготавливаются и
эксплуатируются в статистически однородных условиях. Эта
теория применима также для единичных ремонтируемых
объектов, в которых допускаются многократные отказы или
если объекты состоят из элементов массового
производства.
Основы теории надежности получили свое развитие в
конце 40-х г. прошлого столетия, в связи с появлением
сложных систем в области радиоэлектроники, авиации и
ракетостроении.
В 60 –е годы прошлого столетия она получила
распространении и на железнодорожном транспорте.
В России с 1990 года действует ГОСТ 27.002-89 в котором
установлены обязательные для применения во всех видах
документов и литературе основные понятия, термины и
определения в области надежности технических объектов.

7.

Теория
надежности
–
наука,
изучающая
закономерности отказов технических объектов
(элементов или систем), поэтому
позволяет
прогнозировать
и
рассчитывать
поведение
объектов при определенных условиях в будущем.
Теория
надежности
изучает
процессы
возникновения отказов объектов (элементов,
систем) как
случайных событий, имеющих
случайную величину,
поэтому общие идеи теории надежности
базируются
на
разделах
математики
изучающих закономерности случайных величин,
т.
е.
теории
вероятности
и
математической статистики.

8. Краткие сведения из теории вероятностей применительно к теории надежности технических средств

Событие - это явление (факт), которое происходит или не происходит.
Достоверным называют событие, которое обязательно произойдет, если будут
осуществлены определенные условия.
Невозможным называют событие, которое заведомо не произойдет, если будут
осуществлены определенные условия.
Случайным называют событие, которое может произойти или не произойти,
если будут осуществлены определенные условия.
Вероятность события - численная мера степени объективной возможности
этого события.
Вероятность достоверного события равна 1, а вероятность невозможного события
равна 0.
Единица измерения вероятностей и диапазон изменения вероятностей любых
событий – числа от 0 до 1.
Случайная величина - величина, принимающая в результате опыта какое-либо
неизвестное заранее численное значение.
Измерение величины показателей надежности выполняется статистическими
методами.
Статистическая вероятность события при увеличении числа опытов всегда
приближается к математической вероятности события.

9.

Разработка показателей надежности, по которым
оценивается надежность объектов, задача ученых и
исследователей, а расчеты показателей надежности,
способы их обеспечения в процессе проектирования и
создания объектов, а также сбор данных об отказах в
процессе эксплуатации или испытания объектов – это
инженерное дело.
Надежность объекта (системы) в основном
закладывается при его проектировании и
изготовлении, а при эксплуатации надежность только
расходуется. Но скорость ее расхода во многом
зависит от методов эксплуатации, квалификации
обслуживающего персонала, условий эксплуатации.
Задача эксплуатационного персонала состоит не в
повышении надежности объекта, а в том, чтобы как
можно дольше сохранять надежность его элементов,
заложенную
в
процессе
проектирования
и
изготовления.

10. Основные понятия, термины и определения надежности в технике по ГОСТ 27.002-89

Надежность – свойство объекта сохранять во
времени и установленных пределах значения всех
параметров, характеризующих способность выполнять
требуемые функции в заданных режимах и условиях
применения, технического обслуживания, хранения и
транспортирования.
Работоспособное состояние объекта - состояние
объекта, при котором значения всех параметров,
характеризующих способность
выполнять заданные
функции, соответствуют требованиям
нормативнотехнической
и
конструкторской
(проектной)
документации (НТД).

11.

Надежность является комплексным свойством, которое
в зависимости от назначения объекта и условий его
применения
может
включать
безотказность,
долговечность,
ремонтопригодность
и
сохраняемость или
определенные сочетания этих
свойств.
Безотказность – свойство объекта непрерывно сохранять
работоспособное состояние в течение некоторого времени
или наработки.
Долговечность
–
свойство
объекта
сохранять
работоспособное состояние до наступления предельного
состояния при
установленной системе технического
обслуживания и ремонта.
Ремонтопригодность
–
свойство
объекта,
заключающееся в приспособленности к поддержанию и
восстановлению
работоспособного
состояния
путем
технического обслуживания и ремонта, а также способность
объекта к предупреждению и обнаружению причин
возникновения отказов.

12.

Сохраняемость – свойство объекта сохранять в заданных
пределах значения параметров, характеризующих
способности объекта выполнять требуемые функции, в
течение и после хранения и (или)
транспортирования.(Особенность при сезонной работе).
Предельное состояние – состояние
объекта, при
котором его дальнейшая эксплуатация недопустима или
нецелесообразна,
либо
восстановление
его
работоспособного
состояния
невозможно
или
нецелесообразно. Это наступает
при
неустранимом
отклонении
величин
заданных
параметров
или
неустранимом нарушении безопасности, а также при
недопустимом увеличении эксплуатационных расходов.

13.

Объекты (системы или элементы)
выполняют
определенную функцию. Если происходит полная или
частичная утрата способности выполнения этой функции, то
такое событие называется отказом.
По ГОСТ 27.002-89 отказ – событие, заключающееся в
нарушении работоспособного состояния объекта.
Признаки или совокупность признаков нарушения
работоспособного состояния объекта устанавливаются в НТД.
В качестве критериев отказа может быть не только
разрушение объекта, но и выход параметра за пределы
заданных отклонений (параметрический отказ), например,
напряжения или частоты в электрической сети, времени
включения или отключения выключателя, температуры
нагрева элементов, сопротивления токопроводящего стыка в
рельсовой линии и т.д.

14. Виды отказов

• - ресурсный отказ, это отказ, в результате которого
объект достигает предельного состояния;
• - независимый отказ, это отказ, не обусловленный
другими отказами;
• - зависимый отказ, это отказ, обусловленный
другими отказами;
• - внезапный отказ, это отказ, характеризующийся
скачкообразным изменением значения одного или
нескольких параметров объекта;
• - постепенный отказ, это отказ, возникающий в
результате постепенного изменения значений одного
или нескольких параметров объекта;
• перемежающийся или сбой - это многократно
возникающий самоустраняющийся отказ объекта
одного и того же характера.

15.

В теории надежности объекты подразделяются на:
- восстанавливаемый объект – объект, для которого в
рассматриваемой ситуации проведение восстановления
работоспособного
состояния
предусмотрено
в
НТД
(допускается ремонт, регулировка, замена отдельных
элементов и т.д.);
- невосстанавливаемый объект – объект, для которого в
рассматриваемой ситуации проведение
восстановления
работоспособного состояния не предусмотрено в НТД
(применяются до первого отказа);
- ремонтируемый объект – объект,
проведение ремонтов предусмотрено в НТД;
для
которого
- неремонтируемый объект – объект, для
проведение ремонтов не предусмотрено в НТД.
которого

16. Исправное состояние объекта характеризуется соответствием всем требованиям НТД. Событие, состоящее в нарушении исправного состояния объ

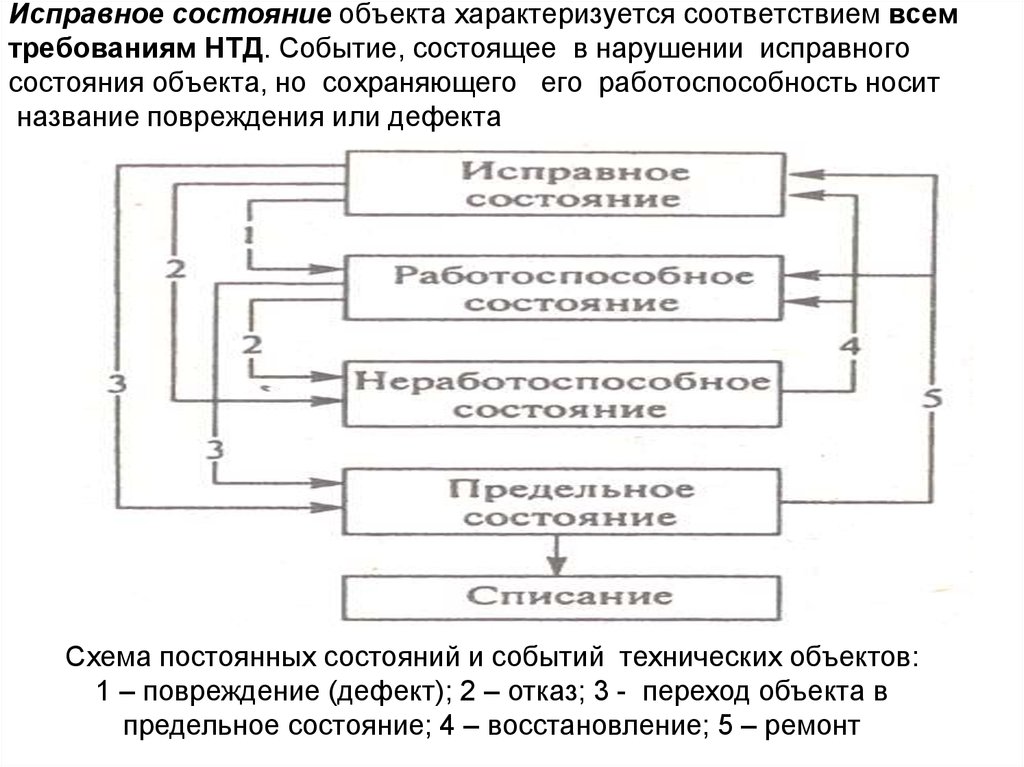
Исправное состояние объекта характеризуется соответствием всем
требованиям НТД. Событие, состоящее в нарушении исправного
состояния объекта, но сохраняющего его работоспособность носит
название повреждения или дефекта
Схема постоянных состояний и событий технических объектов:
1 – повреждение (дефект); 2 – отказ; 3 - переход объекта в
предельное состояние; 4 – восстановление; 5 – ремонт

17.

При расчете надежности функционирования объектов
интересуются
продолжительностью
или
объемом
выполненной
ими
работы.
При
этом
пользуются
обобщенным понятием «наработка». Под наработкой
объекта
устройств
ЭНС,
АТ
и
ТС
понимается
продолжительность или объем работы объекта, измеряемые
в единицах времени, числах объектов, циклов или оборотов
и т.д.
При рассмотрении невосстанавливаемых объектов
случайной является
наработка объекта от начала
эксплуатации до возникновения первого отказа.
Для восстанавливаемых объектов
случайной
является
наработка
между
двумя
последовательными отказами.

18.

Наработка может рассматриваться в двух аспектах как величина случайная и как
величина заданная
(неслучайная).
Отказ объекта является событием случайным, а время
до его возникновения- случайная величина.
Полной характеристикой любой случайной величины
является ее закон распределения. Напомним!
Законом распределения случайной величины
называется всякое соотношение, устанавливающее
связь между
возможными значениями случайной
величины и соответствующими им вероятностями.
При определении надежности технических устройств
наиболее часто применяются следующие законы
распределения
времени
безотказной
работы:
экспоненциальный, нормальный и Вейбулла.

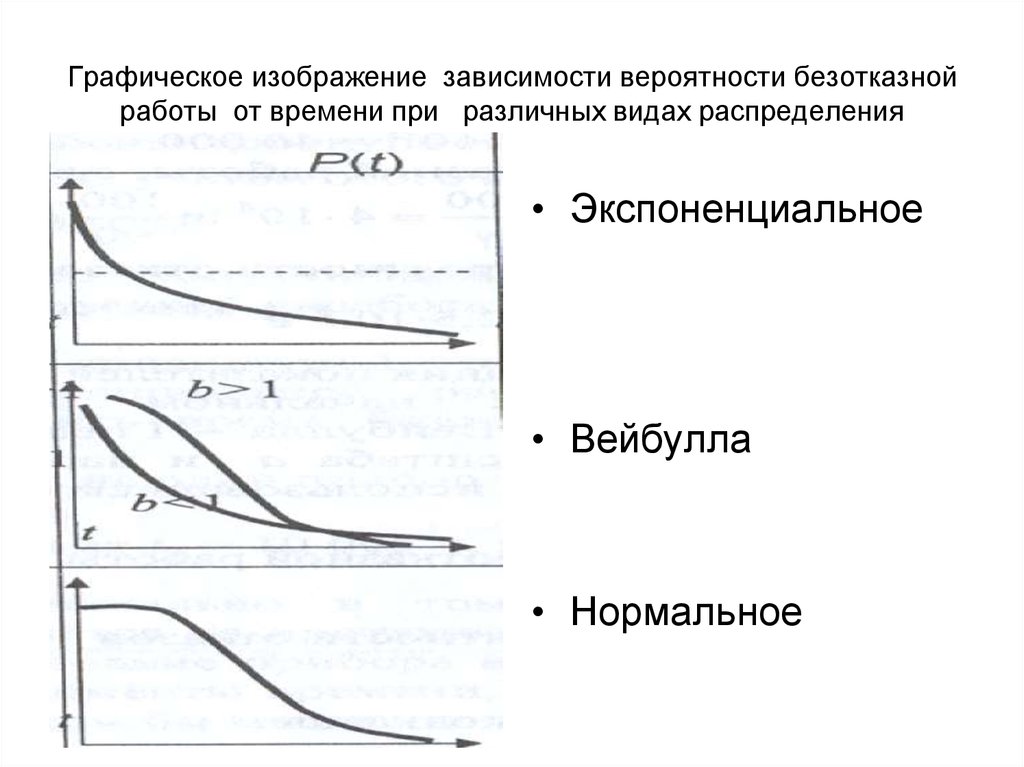
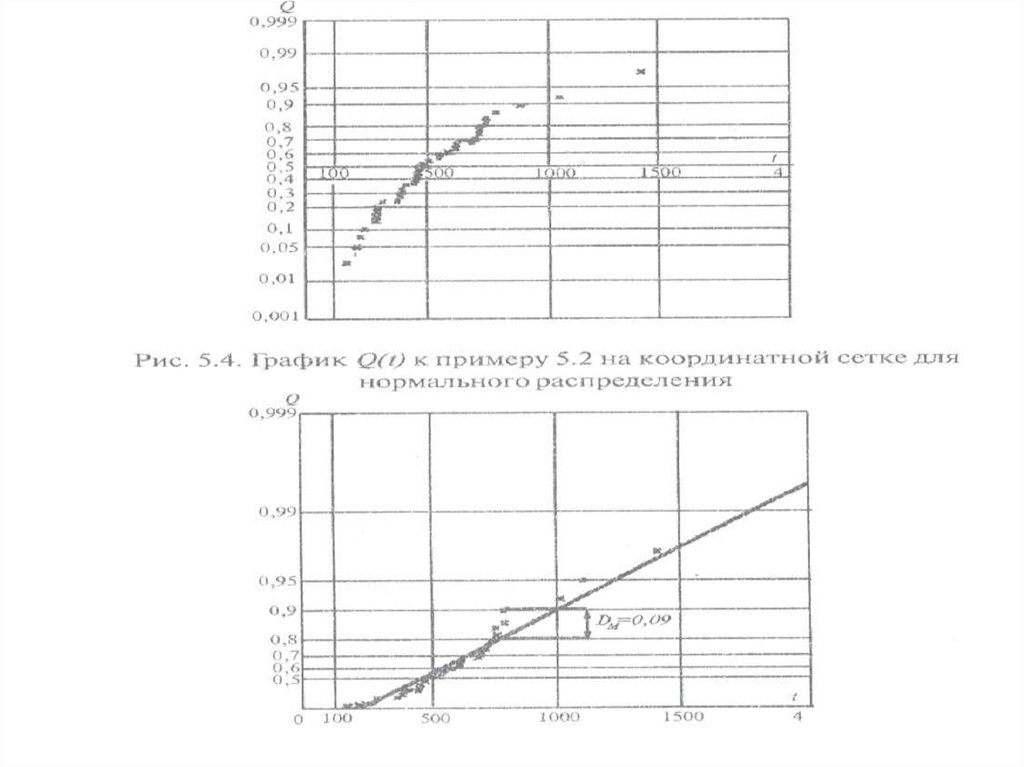
19. Графическое изображение зависимости вероятности безотказной работы от времени при различных видах распределения

• Экспоненциальное
• Вейбулла
• Нормальное

20. Количественные показатели надежности невосстанавливаемых объектов

Для
количественной
оценки
надежности
невосстанавливаемых
объектов
используют
вероятностные характеристики случайной величины –
наработки до отказа.
Когда наработку до отказа выражают в единицах
времени, используют термин «время безотказной
работы». При этом за единицу времени принимается,
как правило, «час», иногда – «год».
Распределение наработки до отказа может быть
описано с помощью таких показателей: функция
надежности; функция ненадежности; плотность
распределения
наработки
до
отказа;
интенсивность отказов; средняя наработка до
отказа; гамма-процентная наработка до отказа.

21.

Функцией
надежности
Р(t)
или
вероятностью
безотказной работы, называют вероятность того, что в
пределах заданной наработки отказ объекта не возникнет. Эту
функцию обозначают
Р(t) =Р(Т t),
где Т – время работы изделия от его включения до первого
отказа (случайная наработка до отказа); t–время, в течение
которого определяется вероятность безотказной работы.
Общие свойства функции надежности Р(t):
-Р(0)=1, т.е. можно рассматривать безотказную работу
лишь тех объектов, которые были работоспособны в момент
начала работы;
- Р(t) является монотонно убывающей функцией заданной
наработки t;
- Р(t) 0 при t , т.е. любой объект со временем откажет.
Таким образом, функция надежности в зависимости от
величины времени может изменяться от 1 до 0.

22.

Функция ненадежности или вероятность отказа Q(t) вероятность того, что при определенных
условиях
эксплуатации в заданном интервале времени произойдет
хотя бы один отказ.
Q(t) = 1- Р(t) =Р (Т< t).
Вероятность отказа – это вероятность того, что
случайное время жизни объекта Т будет меньше наперед
заданного времени t, в течение которого определяется
вероятность отказа.
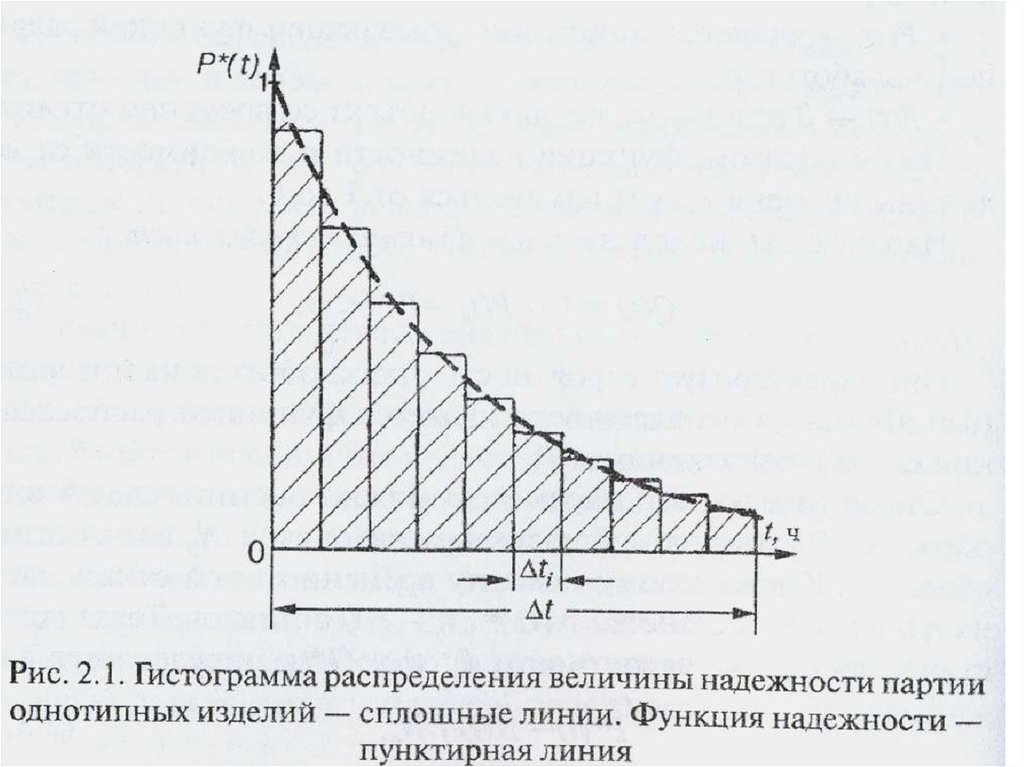
Статистически параметры Р*(t) и Q*(t) определяется как
Р*(t)= N (t) / N0 ,
Q*(t)=1- N (t) / N0 =r(t)/N0,
(!)
(!)
где N0 – число однотипных объектов находящихся под
наблюдением;. r(t)- число объектов отказавших к моменту
времени t ; N(t) = N0 - r(t) – число объектов оставшихся в
работе к этому времени.
В отличие от математических величин, статистические
оценки величин обозначаем *.

23.

24.

25.

Статистическая оценка Р*(t) и Q*(t) мало отличается
от Р(t) и Q(t) только при больших значениях N0 и r.
Плотность распределения наработки до отказа (t)
является дифференциальной формой закона
распределения наработки до отказа
(t)= dQ(t)/dt =-dP(t)/dt.
Плотность вероятности отказа - характеризует скорость
изменения функций Р(t) и Q(t) и измеряется в единицах в
час (год).
В математической статистике её называют частотой
отказов и обозначают (t)
(t)=r( t)/(N0 t),
(!)
где t - интервал времени, за который произошло
r( t) отказов.

26.

Зависимость частоты и интенсивности отказов объекта от времени

27.

Интенсивность отказов (t) - условная плотность
вероятности возникновения отказа
(t) = (t)/Р(t).
Интенсивность отказов измеряется в единицах в час (год).
Статистически интенсивность отказов равна отношению
числа отказавших изделий в единицу времени к среднему
числу изделий, исправно работающих в данный отрезок
времени
*(t) = (t)/ Р(t) = r( t )/ (Nср t), (!)
где Nср= ( i+ i+1)/2 –
-среднее число исправно работающих изделий в интервале
t;
i- число изделий, исправно работающих в начале
интервала t;
i+1 –число изделий, исправно работающих в конце
интервала t.

28. График зависимости интенсивности отказов  от времени t называется характеристикой жизни объекта

График зависимости интенсивности отказов от
времени t называется характеристикой жизни объекта
1- нормальный режим; 2 – нагруженный режим; 3 – облегченный
режим; I – приработка; II – нормальный режим; III - деградация

29. Интенсивность отказов объекта однозначно определяет вероятность безотказной работы в соответствии с основной формулой надежности Р(t) = е

Интенсивность отказов объекта однозначно
определяет вероятность безотказной работы в
соответствии с основной формулой
надежности
Р(t) = ехр - (t) dt .
0
.

30.

Для освоенного и отработанного оборудования
интенсивность отказов в пределах периода его
работы можно полагать постоянной.
В этом случае все показатели надежности
существенно упрощаются и принимают вид
Р(t)= ехр(- t); Q(t)=1- ехр(- t). (!)
Таким образом, функция распределения времени
безотказной работы становится экспоненциальной
функцией. Соответственно дифференциальная
характеристика, т.е. плотность распределения
функции
(t)=dQ(t)/dt= ехр(- t).
(!)

31.

Среднее время безотказной работы – среднее
время наработки объектов до первого отказа, т. е. это
время
математического
ожидания
времени
безотказной работы технического объекта (m). Ее
вероятностная форма имеет следующий вид при при
=const.
t
t
m= Р(t) dt = exp(- t)dt = 1/ .
0
(!)
0
Среднее время безотказной работы является
интегральным показателем надежности, т.е. за длительное
время работы объекта. В этом ее недостаток, а достоинством
можно считать – высокую наглядность. Статистическая
оценка средней наработки до отказа
при N(t) 0 может быть получена как
m*=tср={ t + tr[N0 –r (t) }/ r(t),
r
i 1
i
где ti- - время до отказа i-го объекта; tr – время
наблюдения за r(t) объектами.

32.

Если во время наблюдения отказали все Nо объекты (No=r), то
m* определяется как среднее арифметическое значение случайной
величины ti.
N0
m*=(1/N 0)
t
i 1
i
(!)
Разброс значения m* характеризуется дисперсией (D ) или
среднеквадратичным отклонением (σ ).
Для экспоненциального распределения
D=1/λ², а σ=√D=m*
Гамма-процентная наработка до отказа tγ определяется как
наработка, в течение которой отказ объекта не возникнет с
вероятностью γ выраженной в процентах
Р(tγ)= ехр(- tγ)= γ/100.
tγ = - (1/ ) ln(γ/100)
или
tγ = m ln(100/γ).
(!)
(!)

33.

На практике наиболее часто используется
показательное (экспоненциальное) распределение.
Это связано с тем, что:
-во-первых, при постоянных интенсивностях отказов
очень простые формулы для оценки показателей
надежности;
-во-вторых, при ограниченных экспериментальных
данных трудно обнаружить значительные
отклонения от гипотезы =const, даже если имеется
некоторая нестационарность (t).
Если экспериментальных данных недостаточно, в
качестве первого приближения принимают =const;
-в-третьих, показательное распределение
наработки до отказа типично для объектов,
состоящих из многих элементов с различными
распределениями до отказа.

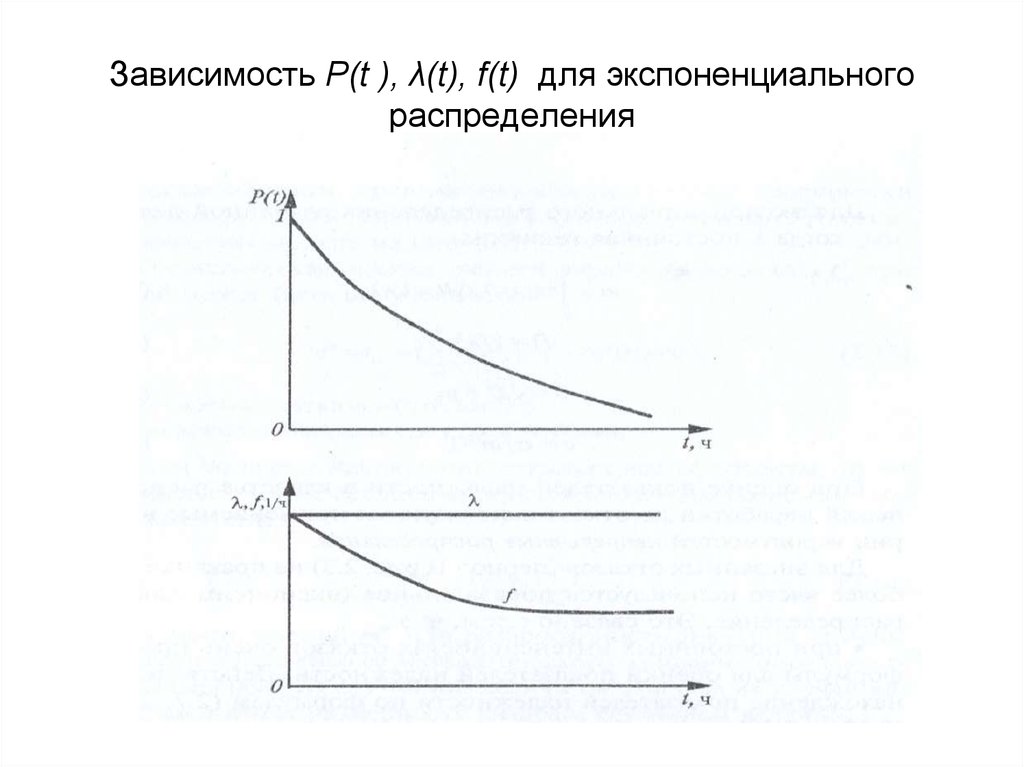
34. Зависимость Р(t ), λ(t), f(t) для экспоненциального распределения

35.

Количественные показатели при
нормальном распределении
Случайная величина обладает нормальным
распределением, когда число факторов, влияющих на
интересующее нас событие, велико, а влияние каждого
из них мало (например, период деградации для участка
- характеристики).
Вычисления при нормальном распределении случайных
величин чрезвычайно сложны.
Для расчета постепенных отказов необходимо знание
двух параметров ( ,m) и для определения вероятности
отказов необходимо интегральные вычисления
плотности вероятности нормального распределения
имеющего сложный вид.

36.

При определении статистических оценок величин m* или
средней наработки
до отказа t ср и используются
выражения
N
m*=( ti )/ N = t ср;
i 1
__________________
= √ ∑( ti-m )2/ (N-1) ,
где N – число объектов или случаев.
Плотность вероятности нормального
функцией
2
1
t m
f (x)
ехр []
2 2
распределения
выражаетс
Вероятность отсутствия отказа на промежутке от 0 до t
находится по формуле
Р(t)= Fо (m-t)/ .
Значения функции нормального распределения Fо(х) в
зависимости от х= (m-t)/ табулированы и приведены в
таблицах соответствующих справочников или учебников.

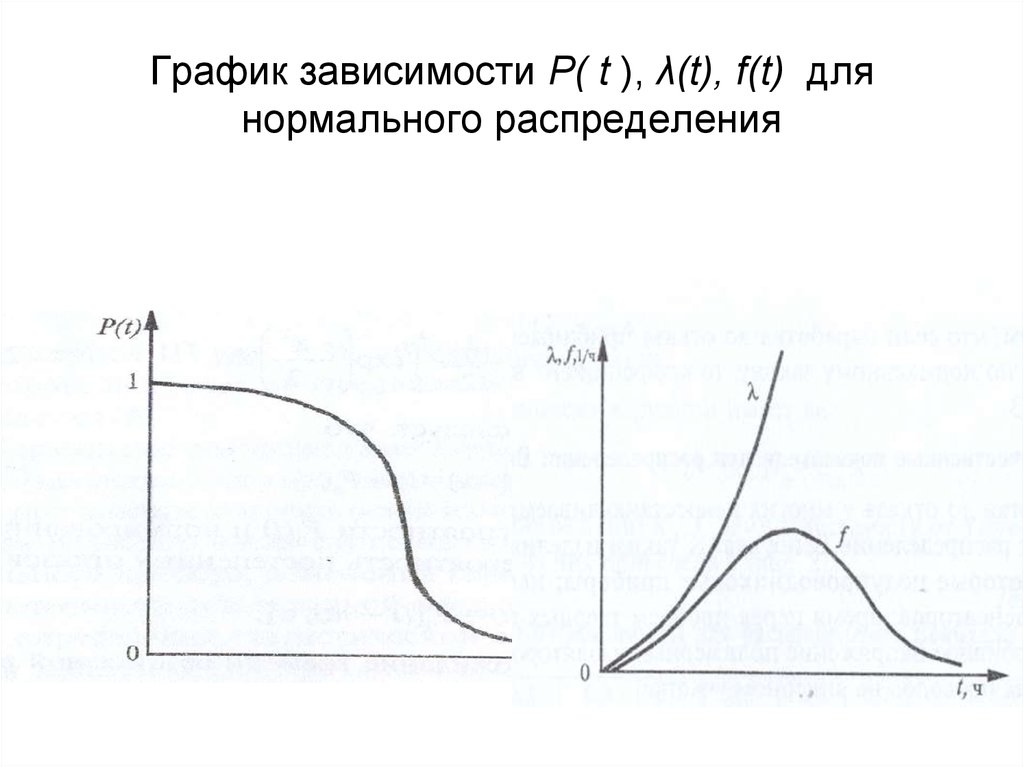
37. График зависимости Р( t ), λ(t), f(t) для нормального распределения

38.

Количественные показатели при сложных событиях
или объектах
Эксплуатация электрооборудования, например, силовых
трансформаторов сопровождается как внезапными
отказами, так и постепенными отказами, обусловленными
тепловым и вибрационным старением изоляции в
резкопеременных режимах электропотребления.
Вероятность такого сложного события равна произведению
вероятностей более простых событий
Р(t)= PвPп= ехр(- t) [ Fо[(m-t)/ ],
где Pв – вероятность того, что за время t в изделии не
произойдет внезапного отказа;
Pп - вероятность того, что за время t в объекте не
произойдет постепенного отказа.

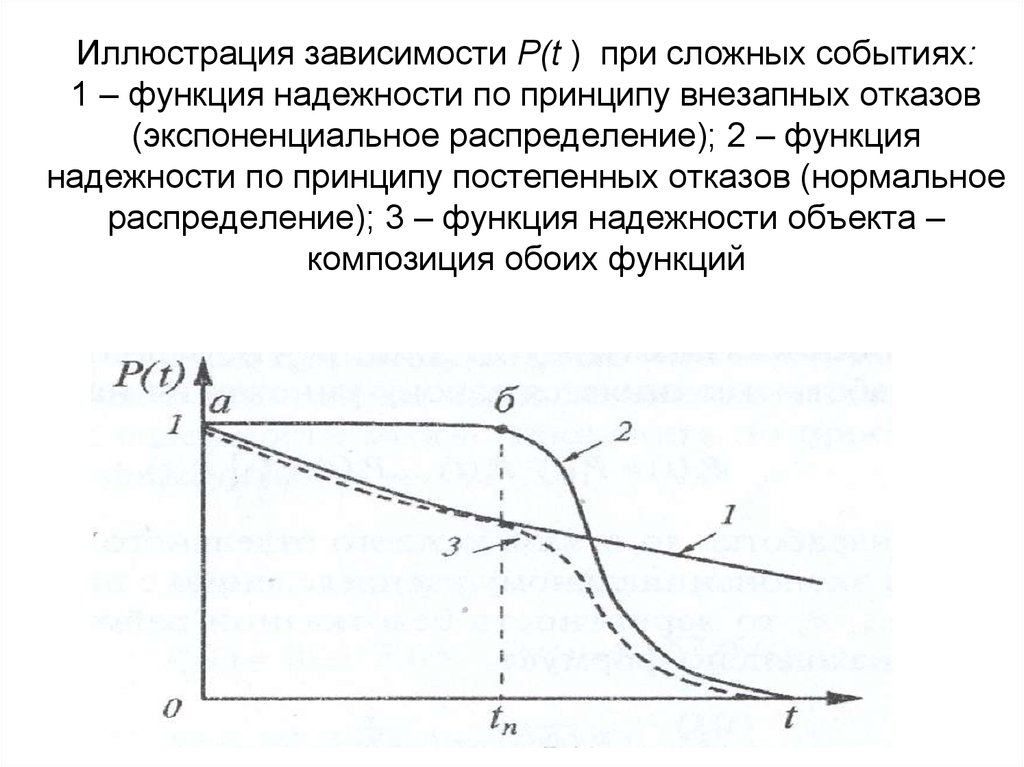
39. Иллюстрация зависимости Р(t ) при сложных событиях: 1 – функция надежности по принципу внезапных отказов (экспоненциальное распределение); 2

– функция
надежности по принципу постепенных отказов (нормальное
распределение); 3 – функция надежности объекта –
композиция обоих функций

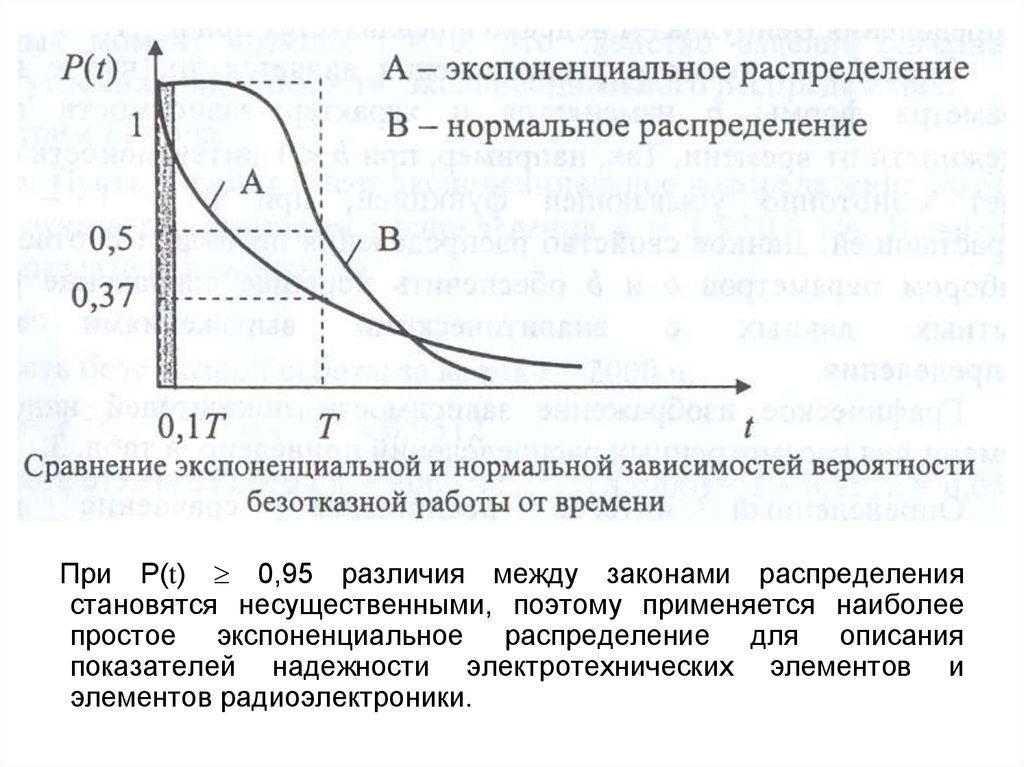
40.

При Р(t) 0,95 различия между законами распределения
становятся несущественными, поэтому применяется наиболее
простое экспоненциальное распределение для описания
показателей надежности электротехнических элементов и
элементов радиоэлектроники.

41. Под сложным объектом понимают объект, состоящий из нескольких одновременно функционирующих отдельных объектов (элементов). Отказ каждого

Под сложным объектом понимают объект, состоящий из
нескольких одновременно функционирующих
отдельных объектов (элементов). Отказ каждого
элемента приводит к отказу сложного объекта. Отказы
отдельных элементов независимы.
Для сложного объекта состоящего из n по признаку
надежности последовательно соединенных отдельных
объектов с показателями безотказности Р1(t),Р2(t)…Рn(t),
вероятность безотказной работы подчиняется закону
умножения надежностей
n
Рс(t )= Р1(t) Р2(t),….. Рn(t) =
Рi(t). (!)
i 1

42.

Если наработка до отказа каждого отдельного объекта
подчиняется экспоненциальному распределению с параметром
k, а k = 1,2,…,n, то вероятность безотказной работы сложного
объекта находят по формуле
n
Р*с(t)=ехр(-t k.) (!)
k 1
Если 1= 2=…= n , то
Р*с(t ) = ехр(-t n ).
(!)
Среднюю наработку до отказа сложного объекта,
состоящего из n элементов, при при 1= 2=…= n
m*с =(n )-1.
(!)

43. Приближенные формулы вычисления показателей надежности высоконадежных объектов, когда Pс(t) >0,9 или t<0.1 Qi(t) – вероятность отказа i-го элеме

Приближенные формулы вычисления показателей
надежности высоконадежных объектов,
когда Pс(t) >0,9 или t<0.1
Qi(t) – вероятность отказа i-го элемента;
n- количество последовательно по надежности
включенных элементов.
при =const
• P(t) =1- t;
Pc(t) = 1-n t = 1- сt ;
n
P
• Pc(t) = i (t) =1-n Qi(t);
• Pi(t) = n Pc (t ) =1-Qс(t)/n.
при const
• Pc(t) = P1(t) ·P2(t) · Pc(t) … Pn(t) =1- Qi(t);
n
i 1

44. Примеры расчета показателей надежности невосстанавливаемых объектов

Пример 1. Наработка объекта до отказа
подчиняется экспоненциальному
распределению с параметром =10-4 1/ч.
Найти вероятность безотказной работы при
t = 1000 ч и среднюю наработку до отказа.
Пример 2. Интенсивность отказов объекта равна
=10-3 1/ч. Найти вероятность безотказной
работы за 10 ч и 20 ч.

45.

Пример 3. При испытаниях 100 изделий в
течение 1000 ч получили 10 отказов. Найти
вероятность безотказной работы, интенсивность
отказов и среднее время безотказной работы .
Пример 4. Средняя наработка изделия до
отказа равна m = tср =10 000ч. Найти наработку t,
отвечающей вероятности Р=0,95.
Пример 5. Интенсивность отказов изоляторов
= 10-6 1/ч. Сколько изоляторов может отказать
за один год, если всего работало 2000
изоляторов?

46.

Пример 6.Средняя наработка до отказа 500 ч.
Определить плотность распределения для момента
времени равного средней наработки до отказа, если
интенсивность отказов постоянна.
Пример 7. Вероятность безотказной работы изделия
Р(200)= 0,99 Каково значение вероятности отказа
для 100 и 300 ч, если интенсивность отказов
постоянна?
Пример 8. Данные по отказам объектов в
зависимости от наработки
время, ч
0 1000 2000 3000 4000 5000
кол. отказов 0
3
5
9
11
14
Определить наработку на отказ за время в
пределах испытаний.

47.

Пример 9. Определить разброс значения m*, полученного в
предыдущем примере и характеризуемый дисперсией (D)
или среднеквадратичным отклонением (σ ).
Пример 10. Схема состоит из четырех одинаковых
последовательно соединенных элементов. Определить
вероятность безотказной работы схемы и среднюю
наработку до отказа схемы, если вероятность безотказной
работы одного элемента Р(1000)=0,995, а интенсивность
отказов элементов постоянна.
Пример 11. Схема состоит из четырех одинаковых
последовательно соединенных элементов. Вероятность
безотказной работы в течение 2000 ч равна 0,98.
Определить интенсивность отказов одного элемента схемы.

48.

12.
Объект
состоит
из
пяти
последовательно соединенных
элементов.
Надежность
элементов
характеризуется
вероятностью безотказной работы в течение
времени t=100 ч, которая равна:P1(t)=0,98;
P2(t)=0,99; P3(t)=0,97; P4(t)=0,985, P5(t)=0,95
Определить
вероятность безотказной работы
объекта и интенсивность отказов при t=200ч.
Пример 13. Вероятность безотказной работы
одного элемента в течение времени t равна P(t) =
0,999. Определить
вероятность безотказной
работы объекта состоящего из n=15
таких
элементов.
Пример

49. Пример 14. Объект состоит из трех последовательно включенных элементов с постоянными интенсивностями отказов. Вероятность безотказной раб

Пример 14. Объект состоит из трех
последовательно включенных элементов с
постоянными интенсивностями отказов.
Вероятность безотказной работы элементов в
течение t часов имеет следующие значения:
Р1(100)=0,99; Р2(200) = 0,97; Р3(150) = 0,95.
Определить вероятность безотказной работы
системы в течение 100 часов ее работы, а также
среднее время безотказной работы.
Пример 15.Вероятность безотказной работы
объекта в течение t равна Рс(t) = 0,95.
Объект состоит из n =6 равнонадежных
элементов, соединенных последовательно.
Определить вероятность безотказной работы
одного элемента.

50.

Пример 16. Определить гамма-процентную
наработку устройства
до отказа tγ при
экспоненциальном распределении, если γ = 95
(время безотказной работы с вероятностью γ =
95%), а интенсивность отказов равна = 10-6 ч-1.
Пример 17. Какова должна быть интенсивность
отказов устройства, чтобы обеспечить гаммапроцентную наработку γ = 95% в течение 15 лет?

51.

Количественные показатели надежности
восстанавливаемых объектов
Восстановление объекта при возникновении отказа
возможно путем ремонта или технического обслуживания,
после чего он вновь используется по назначению.
Время восстановления определяется многими
факторами (время обнаружения отказа, время доставки
. бригады, время работы, и т.д.), поэтому является
случайной величиной.
Показатели надежности восстанавливаемых объектов
рассчитывают на основе учета наработки между отказами и
временем восстановления.
Потоком событий называется последовательность
событий, наступающим один за другим в случайные
моменты времени.

52.

53.

Если
не
учитывать
времени,
потребного
на
восстановление
объекта,
то
количественной
характеристикой
надежности
восстанавливаемых
объектов могут быть параметр потока отказов ( ) и
средняя наработка на отказ (tоср).
Параметром потока отказов называется скорость
изменения среднего числа отказов объекта в момент t.
Статистически параметр потока отказов определяется по
формуле
=n(∆t)/(N ·∆t),
n(∆t) – число отказавших объектов в интервале времени
(∆t);
N – число испытуемых образцов.

54.

Оценку значения tоср определяют по формуле
tоср=(tо1+tо2+..+tоn)/n= (∑tоi)/n=mо,
где n – число отказов объекта за время эксплуатации
t;
tоi - время исправной работы объекта между (i-1) и i-м отказами объекта.
Количественную оценку ремонтопригодности
дает среднее время восстановления одного отказа
(tвср).
n
tвi/n=mв,
tвср=(tв1+tв2+..+tвn)/n=
(!)
i 1
где tвi -время восстановления объекта после i -го отказа;
n – число отказов или восстановлений объекта за время
эксплуатации t.

55.

Время между соседними отказами распределено по
экспоненциальному закону, если потоки отказов и
восстановлений являются простейшими (пуассоновскими),
т.е. обладают свойствами ординарности, стационарности и
отсутствия последействия.
Поток событий (отказов объектов) называется
стационарным, если его вероятностные характеристики не
зависят от времени ( п = const).
Потоки отказов объектов являются ординарными, если
вероятность появления двух и более отказов в один и тот
же момент времени пренебрежимо мала.
Поток событий называется потоком без последствий,
если для любых двух непересекающихся участков
времени число событий, попадающих на один из них, не
зависит от того, сколько событий выпало на другом .

56. В период нормальной эксплуатации при расчетах надежности систем ЭНС,АТ и ТС потоки отказов и восстановлений систем принимаются как просте

В период нормальной эксплуатации при расчетах
надежности систем ЭНС,АТ и ТС потоки отказов и
восстановлений систем принимаются как простейшие
(пуассоновские), т.е. их закономерности подчиняются
распределению Пуассона.
По закону Пуассона вероятность возникновения х
отказов в течение времени t определяется по формуле
x
t
Рх(t)=
exp( t ) ,
x!
где -параметр потока отказов.
Вероятность отсутствия отказов (х=0) в течение
времени t указывает на то, что время между соседними
отказами в простейшем потоке распределяется по
экспоненциальному закону
Р(t)= exp( - t).

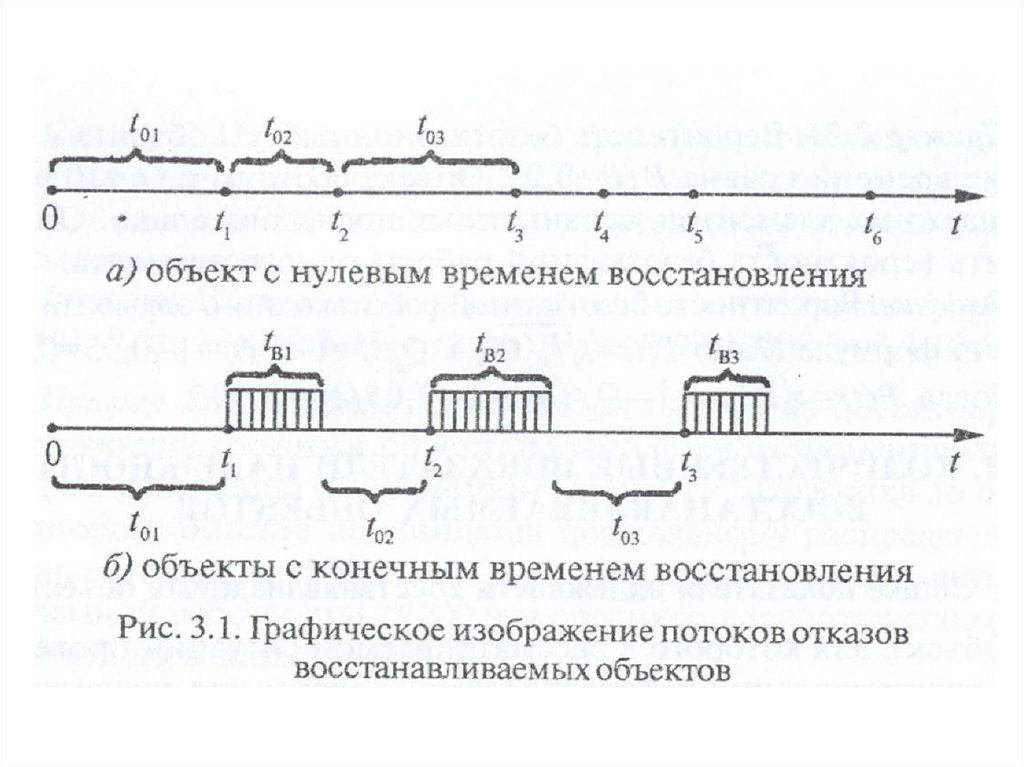
57. Комплексные показатели надежности восстанавливаемых объектов

Для объектов с конечным временем восстановления
применяют численные комплексные показатели
надежности. Их определения дано в ГОСТ 27.002-89.
Коэффициент готовности - вероятность того, что объект
окажется в работоспособном состоянии в произвольный
момент времени, кроме планируемых периодов, в течение
которых применение объекта по назначению не
предусматривается
kг= tр/(tр +tв )≈ mо/(mо+mв),
(!)
где tр – суммарное время исправной работы объекта за
определенный календарный срок; tв – суммарное время
затраченного на восстановления объекта или суммарное
время вынужденного простоя за тот же календарный срок;
mо - математическое ожидание наработки на отказ;
mв - математическое ожидание времени восстановления

58.

Коэффициент готовности определяется только
средним временем работы объекта и средним
временем восстановления вне зависимости от законов
распределения.
Коэффициент kг нельзя применять для оценки
надежности технических систем кратковременного
использования. Он характеризует вероятность того , что
объект будет исправным при длительной эксплуатации.
Коэффициент (вынужденного) простоя характеризует вероятность нахождения объекта в
неработоспособном состоянии, т.е. того, что объект
будет неисправным при длительной эксплуатации
kп = 1- kг= mв/(mо+mв),
(!)

59.

Коэффициент оперативной готовности – вероятность
того, что объект окажется в работоспособном состоянии в
произвольный момент времени, кроме планируемых
периодов, в течение которых применение объекта по
назначению не предусматривается, и проработает
безотказно в течение заданного интервала времени.
Для случая, когда время между отказами и время
восстановления имеют экспоненциальное распределение
kог = kгехр(- t).
(!)
Вероятное время нахождения одного объекта в ремонте
(аварийном простое) за время t вычисляется по формуле
Vi(t)=mв(1-ехр(- t)).
(!)
Вероятное время нахождения объекта в ремонте
(аварийном простое), состоящего из n последовательно
соединенных элементов за время t вычисляется по формуле
Vс(t)=1-Π(1- Vi)=1-(1- Vi ) ⁿ
(!)

60.

При определении или назначении показателей
надежности для восстанавливаемых объектов
используются показатели долговечности.
Полный средний ресурс (технический ресурс) –
математическое ожидание ресурса – представляет собой
среднюю наработку объекта от начала эксплуатации до
наступления
предельного
состояния
с
учетом
восстановления. Полный средний ресурс подразумевает
снятия объекта с эксплуатации по достижению
предельного состояния.
Средний ресурс указывается , если после достижения
предельного состояния объект подлежит капитальному
ремонту.
гамма - процентный ресурс – наработка, в течение
которой объект не достигнет предельного состояния с
заданной вероятностью γ, выраженной в процентах;

61. Средний срок службы - математическое ожидание срока службы – представляет собой среднюю календарную продолжительность эксплуатации объе

Средний срок службы - математическое ожидание
срока службы – представляет собой среднюю
календарную продолжительность эксплуатации объекта
от ее начала до наступления предельного состояния с
учетом восстановления.
гамма - процентный срок службы – календарная
продолжительность от начала эксплуатации объекта, в
течение которой он не достигнет предельного состояния
с заданной вероятностью γ, выраженной в процентах.
Назначенный ресурс (назначенный срок службы) –
суммарная наработка (календарная продолжительность
эксплуатации) объекта, при достижении которой
применение по назначению должно быть прекращено.

62. Примеры расчета показателей надежности восстанавливаемых объектов

Пример 1. Восстанавливаемая система с показательными
распределениями времени безотказной работы и времени
восстановления имеет коэффициент готовности kг = 0,995.
Вычислить вероятность безотказной работы системы в
течение наработки (10) ч, если среднее время
восстановления mв = 5ч.
Пример 2. Восстанавливаемая система с показательными
распределениями времени безотказной работы и времени
восстановления имеет коэффициент простоя kп = 0,009.
Вычислить вероятность отказа системы на момент времени
равной половине средней наработке на отказ, если
среднее время восстановления mв = 10ч.
Пример 3. За 6 дней установка имела три отказа, на ремонт
потребовалось 1,5ч, 2,5ч и 3 ч. Определить коэффициент
простоя установки и ее наработки на отказ.

63.

4. За период эксплуатации трех однотипных
выключателей зафиксировано: на первом 10 отказов за 181 ч;
на втором 10 отказов за 329 ч; на третьем 10 отказов за 245ч.
Требуется определить наработку выключателей на отказ.
Пример
Пример 5.Интенсивность отказов объекта =0,05ч-1, а среднее
время восстановления tср =10ч. Требуется
вычислить
коэффициент готовности и коэффициент оперативной
готовности объекта на момент работы 5 ч.
Пример 6. Объект состоит из
четырех последовательно
соединенных элементов. Интенсивность отказов каждого
элемента =0,05 год-1, среднее время простоя mв = 10-3год.
Определить вероятное время простоя объекта в течение
одного года.

64. Основным методом повышения надежности системы является резервирование.

Согласно ГОСТ 27.002-89 резервирование - это способ
обеспечения надежности объекта за счет использования
дополнительных средств и (или) возможностей,
избыточных по отношению к минимально необходимым
для выполнения требуемых функций.
Различают следующие виды резервирования: временное,
информационное, функциональное, нагрузочное и
структурное.
Структурное резервирование основано на
использовании избыточных элементов структуры объекта.
По способу включения резервных элементов структурное
резервирование подразделяется на: резервирование
замещением (активное), постоянное (пассивное) и
скользящее резервирование.

65.

При резервирование замещением, функции основного
элемента передаются резервному только после отказа
основного элемента. Для включения резерва
предусматриваются переключательные элементы.
При включении резерва резервные элементы до момента
включения в работу могут находиться в трех режимах:
- нагруженном («горячем» состоянии);
- облегченном («теплом» состоянии);
- ненагруженном («холодном» состоянии).
Скользящее резервирование- это резервирование
замещением, при котором группа основных элементов
объекта резервируется одним или несколькими резервными
элементами, каждый из которых может заменить любой
отказавший элемент в данной группе.
При постоянном резервировании резервные элементы
включены постоянно, т.е. резервирование происходит без
перестройки объекта при возникновении отказа его элемента.

66.

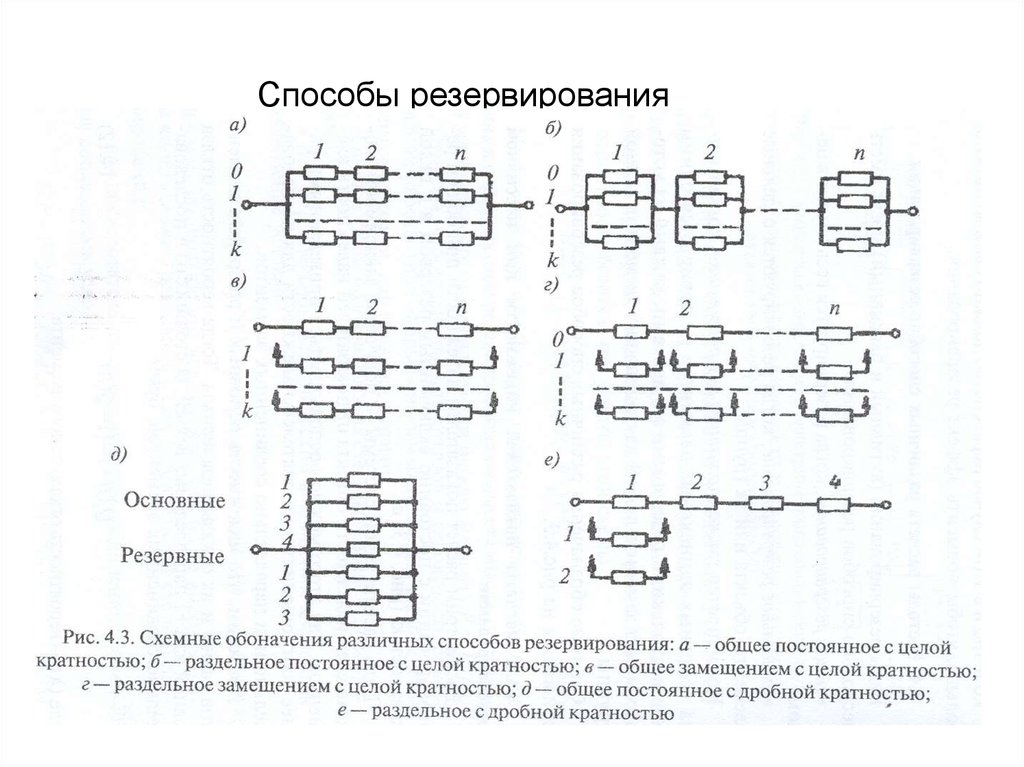
Способы резервирования

67.

Основным параметром резервирования является его
кратность. Под кратностью резервирования понимается
отношение
числа резервных элементов к числу
резервируемых ими элементов, выраженное несокращенной
дробью.
Если это отношение – число целое, то такое
резервирование называется резервированием с целой
кратностью, иначе – с дробной кратностью.
При резервировании с дробной кратностью для нормальной
работы резервированного соединения число исправных
элементов должно быть не менее необходимого.
Кратность резервирования определяется из соотношения
К= (N-h)/h=k/h,
(!)
где N- общее число элементов резервированного объекта;
h – число элементов необходимых для нормальной работы
объекта; k– число резервных элементов.

68. Для повышения надежности отдельного элемента параллельно (по принципу надежности) подключаются аналогичные элементы. Система в этом случ

Для повышения надежности отдельного элемента параллельно (по
принципу надежности) подключаются аналогичные элементы.
Система в этом случае будет работоспособной, если хотя бы один
из ее элементов находился в исправном состоянии. Вероятность
отказа системы с параллельно включенными k+1 элементами равна
произведению отказов элементов.
Функция ненадежность такой системы равна
к+1
Qс(t)=
ΠQi(t),
i=1
где Qi(t)- функция ненадежности i -го элемента.
(!)

69.

Функцию надежности системы с k+1 параллельно
включенными элементами вычисляют по формуле
k 1
Рс(t )= 1- Qс(t)= 1- 1-Pi(t) ,
i 1
(!)
где Pi(t) – вероятность безотказной работы i -го
элемента.
Часто для повышения надежности параллельно
включаются два элемента с одинаковыми
интенсивностями отказов ( 1= 2= ), тогда вероятность
безотказной работы системы и математическое
ожидание наработки системы можно вычислить по
формуле
Р*с(t)= 1- 1-ехр(- t) 2;
(!)
m*с=1/ (1+1/2)= 1,5/ .
(!)

70.

Для случая i= при k+1 параллельно
включенных элементах вероятность безотказной
работы приближенно можно вычислить по
формуле
Р*с(t)=1-( t)k+1,
а среднее время безотказной работы системы
по формуле
m*с = m* [1+1/2+ …+1/(k+1)],
где m* - среднее время безотказной работы
одиночного элемента

71.

Особенностью большинства электрических
элементов является наличие двух видов отказов,
которые приводят объект в неработоспособное
состояние: это обрыв и короткое замыкание.
Поэтому вероятность безотказной работы
элемента является сложным случайным событием и
оценивается произведением вероятностей обоих
видов отказов
Рэ=РоРз=(1- Qо)(1-Qз),
где Qо -вероятность отказа типа «обрыв»;
Qз - вероятность отказа типа «замыкание».

72.

Резервирование отказа типа «обрыв» требует
параллельного включения резервных элементов, а
резервирование отказов типа «замыкание» требует
последовательного включения резервных
элементов.
Вероятность безотказной работы схемы с
параллельным включением двух элементов
Рс=РпоРпз=[1-(1-Ро)2]Р2з=(2Ро-Р2о)Р2з ,
где Рпо -вероятность безотказной работы двух
параллельно соединенных элементов (отказы типа
обрыв);
Рпз - вероятность безотказной работы двух
последовательно соединенных элементов (отказы
типа замыкание).

73.

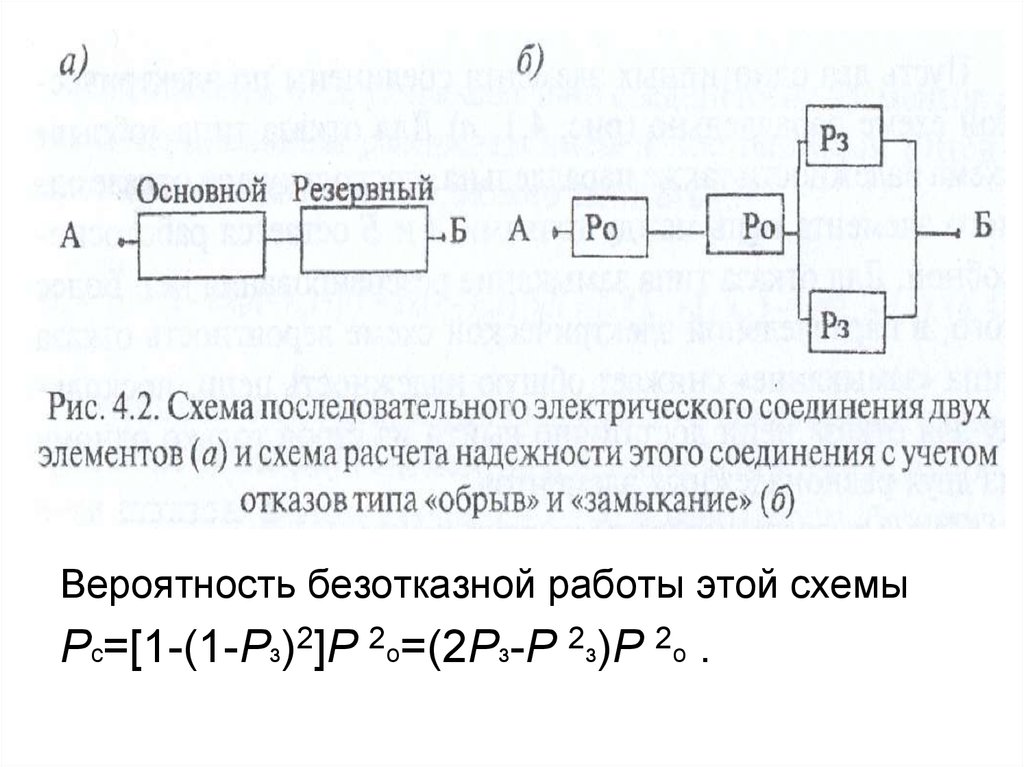
74.

Вероятность безотказной работы этой схемы
Рс=[1-(1-Рз)2]Р 2о=(2Рз-Р 2з)Р 2о .

75.

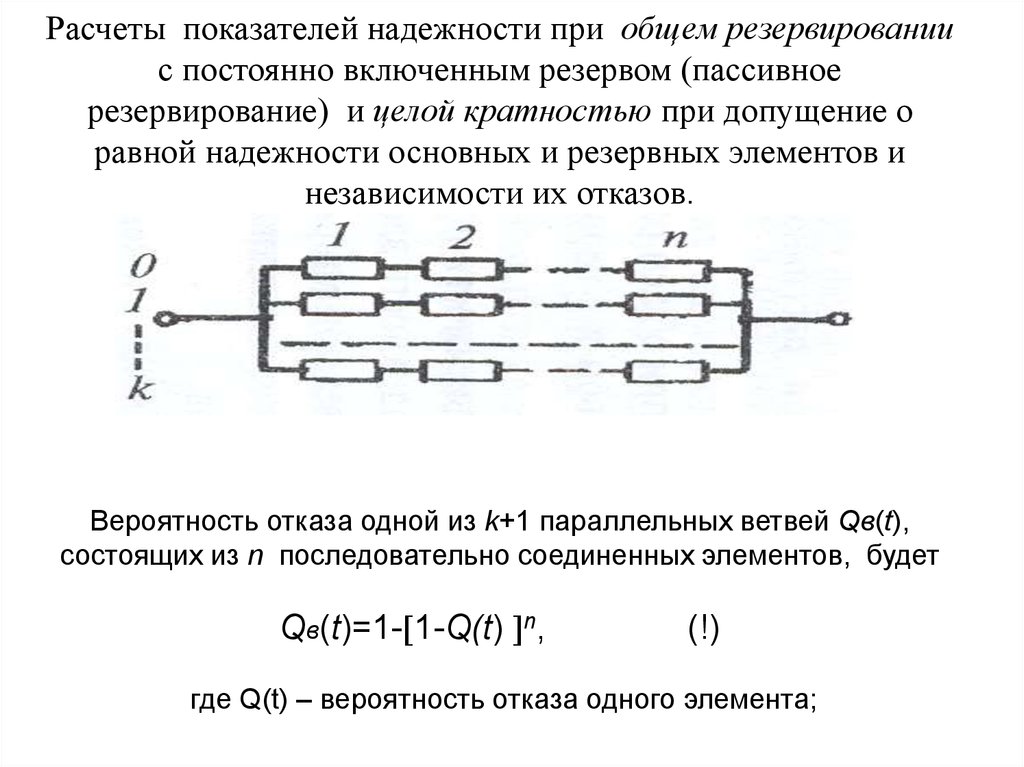
Расчеты показателей надежности при общем резервировании
с постоянно включенным резервом (пассивное
резервирование) и целой кратностью при допущение о
равной надежности основных и резервных элементов и
независимости их отказов.
Вероятность отказа одной из k+1 параллельных ветвей Qв(t),
состоящих из n последовательно соединенных элементов, будет
Qв(t)=1- 1-Q(t) n,
(!)
где Q(t) – вероятность отказа одного элемента;

76.

Вероятность отказа всей системы из k резервных
ветвей и одной основной ветви
Qс= Qв(t) k+1 = 1- 1-Q(t) n k+1.
При равнонадежных устройствах и показательном
распределении наработки до отказа
Робщ(t)=1- 1-ехр (-n t) k+1
(!)
где - интенсивность отказа одного устройства.
Среднее время безотказной работы
1
n
k
1
.
i 0 i 1
m*общ =
Кратность резервирования определяется по формуле:
К= lnQc(t)/lnQв(t) -1
(!)
11 kk 11
..
nn i i 00 ii 11

77.

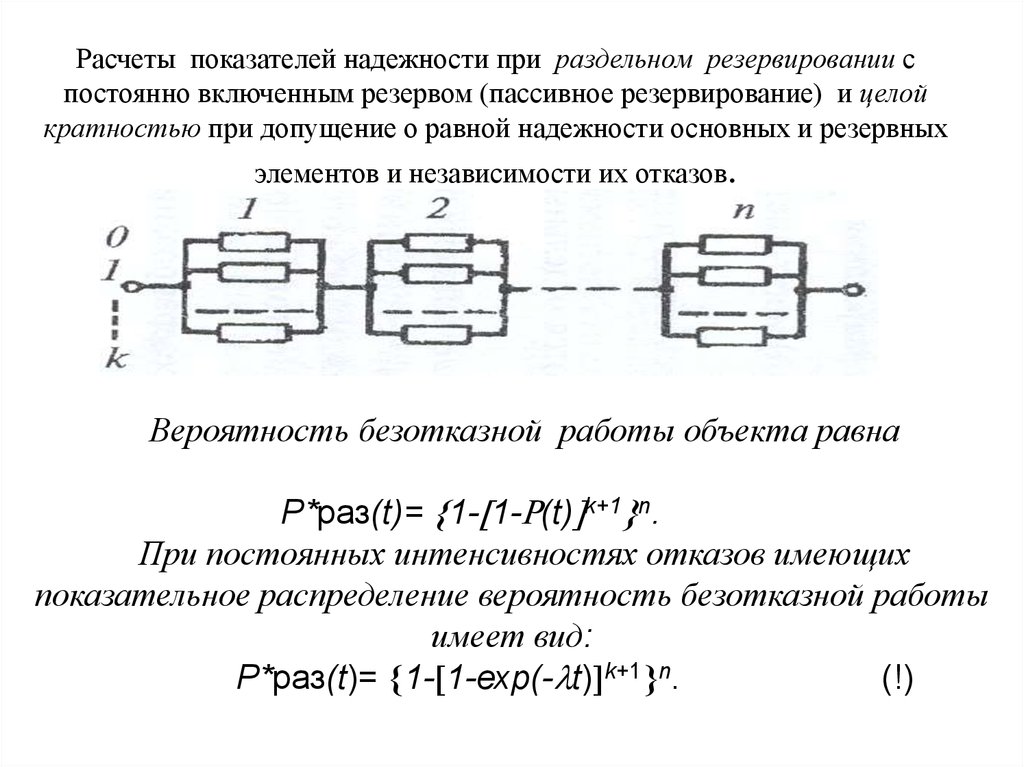
Расчеты показателей надежности при раздельном резервировании с
постоянно включенным резервом (пассивное резервирование) и целой
кратностью при допущение о равной надежности основных и резервных
элементов и независимости их отказов.
Вероятность безотказной работы объекта равна
Р*раз(t)= 1- 1- (t) k+1 n.
При постоянных интенсивностях отказов имеющих
показательное распределение вероятность безотказной работы
имеет вид:
Р*раз(t)= 1- 1-ехр(- t) k+1 n.
(!)

78.

Для дублированного объекта из двух элементов
(n=2):
Р*раз(t)= 1- 1-ехр(- t) 2 2. (!)
Математическое ожидание или средняя
наработка до отказа в этом случае равна
m*раз = 0,916/ ,
где - интенсивность отказов одного элемента.

79.

Резервирование с дробной кратностью
При экспоненциальном законе распределения функция
надежности объекта вычисляется по формуле
n k
Р*др(t) = C ni exp t n i 1 ехр t i
i 0
где ехр(- t) – вероятность безотказной работы основного
или любого резервного элемента;
n – общее число основных и резервных элементов;
k-число элементов, необходимых для нормальной работы
резервированного объекта;
Сni -сочетание из n элементов по i.
Средняя наработка до отказа вычисляется по формуле
m*др=
1
n k
i 0
1
k i

80. Расчеты показателей надежности при активном резервировании

Вероятность безотказной работы и средняя наработка
до отказа объекта при общем резервировании
замещением холодным резервом определяется по
формуле
P*озх(t)=ехр(- t) ;
m*озх=m*о(k+1),
где , mо - интенсивность отказов и средняя наработка
до отказа основного (нерезервированного) элемента.

81.

При расчете показателей надежности объекта с
общим резервированием замещением и целой
кратностью при нагруженном резерве формулы
для определения Р(t) и tср = m совпадают с
формулами для пассивного резервирования
Розг(t)=1- 1-ехр (-n t) k+1,
где - интенсивность отказа одного устройства.
Среднее время безотказной работы
m*озг =
1 k 1
.
n i 0 i 1

82. Примеры расчета показателей надежности резервированных объектов

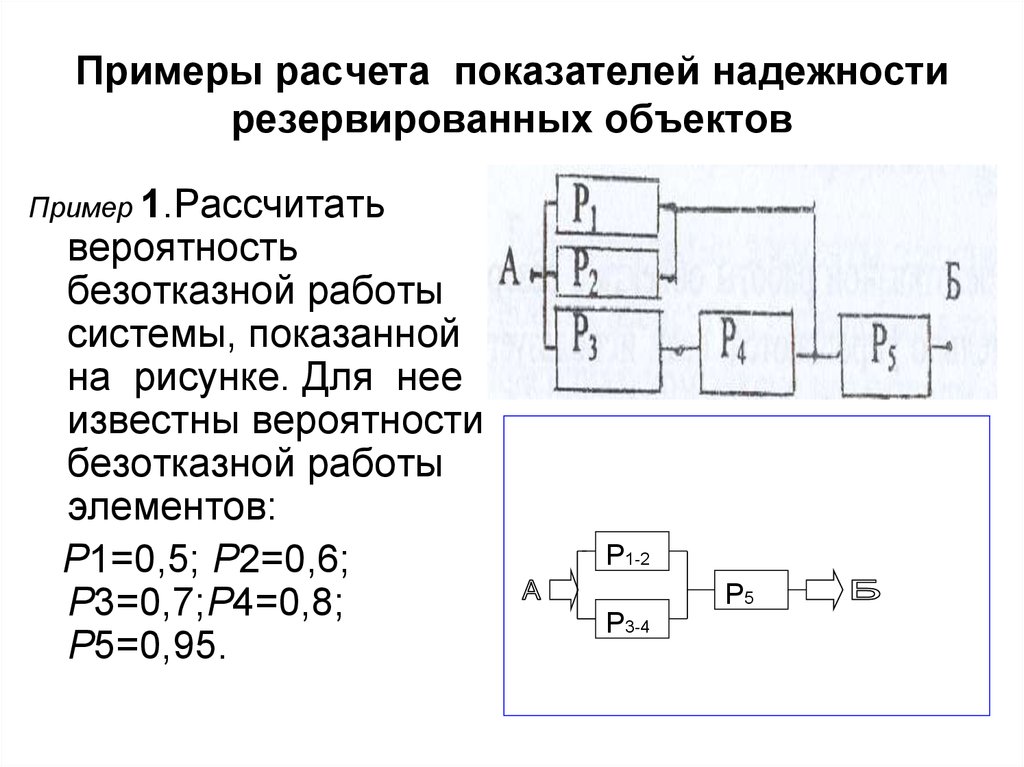
Пример 1.Рассчитать
вероятность
безотказной работы
системы, показанной
на рисунке. Для нее
известны вероятности
безотказной работы
элементов:
Р1=0,5; Р2=0,6;
Р3=0,7;Р4=0,8;
Р5=0,95.
Р1-2
Р3-4
Р5

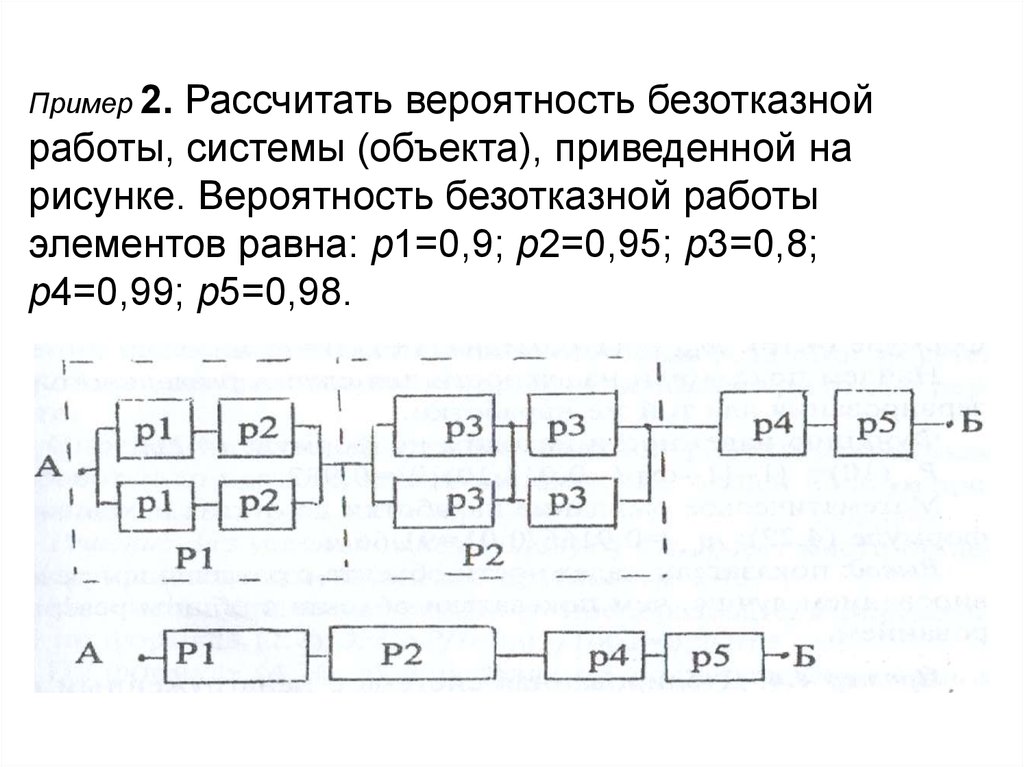
83.

Рассчитать вероятность безотказной
работы, системы (объекта), приведенной на
рисунке. Вероятность безотказной работы
элементов равна: р1=0,9; р2=0,95; р3=0,8;
р4=0,99; р5=0,98.
Пример 2.

84.

Пример 3. Устройство состоит из двух равнонадежных
блоков соединенных последовательно. Интенсивность
отказов каждого блока =0,001ч-1. Отказ устройства
происходит при отказе хотя бы одного блока. С целью
повышения
надежности
предлагается
ввести
дублирование.
Требуется
определить
какой
вид
резервирования (общий или раздельный) оптимальный
при наработке 100 ч.
Пример 4. Определить вероятность безотказной работы
системы и среднее время безотказной работы системы
при
четырехкратном
общем
и
раздельном
резервировании, если
система состоит из четырех
элементов, а интенсивность отказов одного элемента при
непрерывной работе в течение 50 ч равна =0,01 ч -1.

85.

Пример 5. В системе электроснабжения имеется преобразователь
переменного тока в постоянный, вероятность безотказной работы
которого в течение 1000 ч равна 0,95. Для повышения надежности
электроснабжения на подстанции имеется такой же преобразователь,
который находится в холодном резерве и включается при отказе первого.
Определить вероятность безотказной работы системы
преобразователей и среднюю наработку одного преобразователя и
системы преобразователей.
Пример 6.Система представляет собой цепочку из 10 равнонадежных
диодов. Интенсивность отказов одного диода =10-4 ч-1. Для повышения
надежности цепочка диодов имеет однократное резервирование.
Предполагается, что справедлив экспоненциальный закон надежности и
основная и резервная цепочки диодов равнонадежны. Необходимо найти
среднюю наработку до первого отказа системы в следующих случаях:
-дублирование осуществлено при постоянном включении резерва;
-дублирование осуществлено при включении резерва по способу
замещения холодным резервом.

86. Пример 7. Установлено, что интенсивность отказов элемента в течение 100 часов составляла =0,0001 1/ч. Определить вероятность безотказной работ

Пример 7. Установлено, что интенсивность отказов
элемента в течение 100 часов составляла =0,0001 1/ч.
Определить вероятность безотказной работы при
резервировании этого элемента таким же элементом,
включенным параллельно, а затем последовательно
когда о = кз =0,5 ;
кз =0,8 и о =0,2 .
Пример 8. Определить кратность резервирования
системы с постоянным резервом, обеспечивающим
вероятность безотказной работы Р(200)= 0,97, если
элементы системы равнонадежны и имеют
экспоненциальное распределение со средним временем
безотказной работы 290 ч.

87. Способы получения данных об отказах

Данные об отказах обычно получают при наблюдениях за
объектами в процессе эксплуатации либо при
проведении специальных испытаний на безотказную
работу.
Информация об отказах должна быть достоверной, полной
и своевременной.
Достоверность данных определяется объективностью и
правильностью фиксации количества отказов, их
характера и условий возникновения.
Своевременность поступления информации
обеспечивается в последние годы за счет использования
АРМ диспетчера.
Приведенные параметры потоков отказов, основном
отображают положение дел на железнодорожном
транспорте в конце прошлого столетия.

88. На железнодорожном транспорте информация об отказах исходит от работников устраняющих отказ, а ее правильность проверяет старший электро

На железнодорожном транспорте информация об
отказах исходит от работников устраняющих отказ, а ее
правильность проверяет старший электромеханик.
В качестве примера можно привести данные для
предельно простой карты отказов техники для
восстанавливаемых систем:
-тип отказавшей системы;
- из-за какого элемента произошел отказ;
- внешние условия возникновения отказа;
- время начала эксплуатации системы;
- дата отказа;
- суммарное время наработки системы от начала
эксплуатации;
- суммарное время наработки системы от
последнего восстановления до данного отказа;
.
- время восстановления

89. Распределение отказов, влияющих на движение поездов

Службы:
• Пути……………………..
66,1%
• СЦБ……………………..
19,5%
• Электрификации и
электроснабжения…….
5,3%
• Перевозок………………
1,5%
• Другие…………………… 7,6%
Системы:
• Электрической
58,0%
централизации………….
• Автоблокировки………..
28%
• Полуавтоматической
блокировки………………
• Другие…………………… 10%
4,0%

90.

Надежность устройств электроснабжения
определяется надежностью элементов контактной
сети и тяговых подстанций.
Оценочное распределение отказов по основным
элементам контактной сети на участках постоянного и
переменного тока
Вид оборудования
Число отказов на 100 Время восстановления,
км контактной сети
ч
Контактные провода
0,615/0,43
1,66
Прочие провода
0,17/0,25
3,0
Фиксирующие
устройства
конструкции
0,1/0,17
6,6
0,1/0,54
1,95
Изоляторы
Примечание.1.
и
В числителе – для участков постоянного тока; в
знаменателе – переменного.2. Доля повреждений по причинам , не
зависящим от надежности контактной сети около 45%.

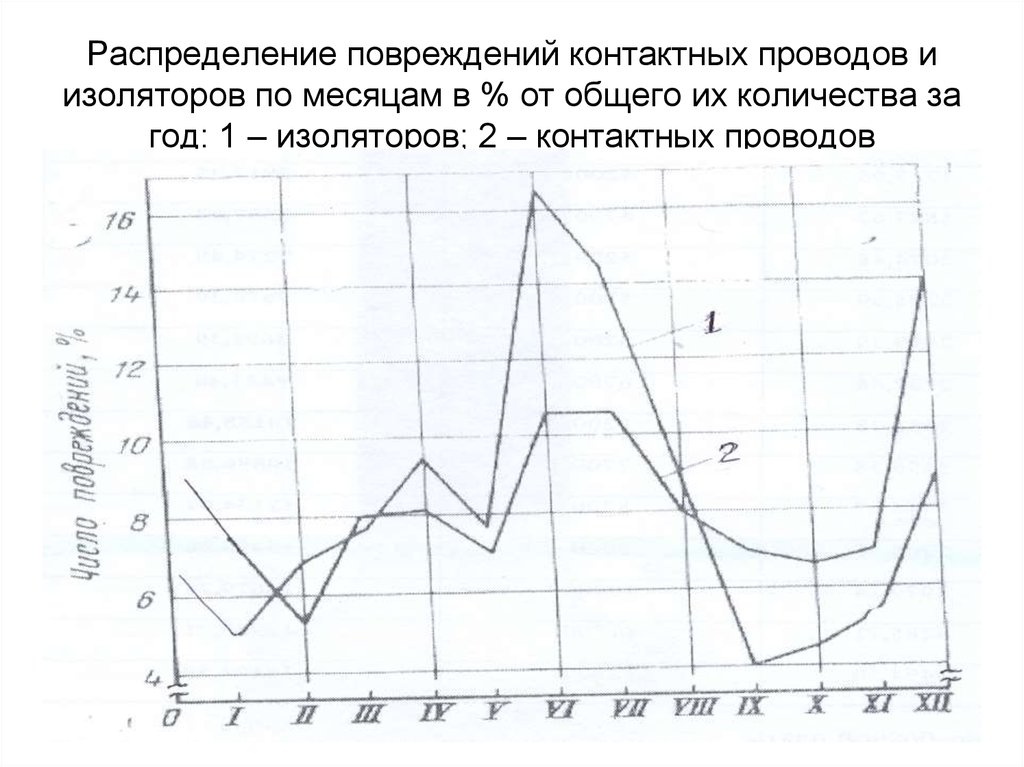
91. Распределение повреждений контактных проводов и изоляторов по месяцам в % от общего их количества за год: 1 – изоляторов; 2 – контактных про

Распределение повреждений контактных проводов и
изоляторов по месяцам в % от общего их количества за
год: 1 – изоляторов; 2 – контактных проводов

92. Оценки показателей наработки оборудования тяговых подстанций постоянного тока Вид оборудования Показатели ,1/год Тяговый трансформатор 0,

Оценки показателей наработки оборудования
тяговых подстанций постоянного тока
Вид оборудования
Показатели ,1/год
Тяговый
трансформатор
Аккумуляторная батарея
Быстродействующий выключатель
Выпрямительный преобразователь
Инверторный преобразователь
0,02
0,008
0,008
0,01
0,016
Примечание. Продолжительность перерывов в движении поездов
из-за повреждений на подстанциях составляет около 3% общего
числа задержек, вызванных неисправностью устройств
электроснабжения.

93.

94.

95.

96. Средние данные интенсивности отказов некоторых элементов массового выпуска, когда =·10-6 ч-1: - двигатели асинхронные  = 8,6; - двигатели по

Средние данные интенсивности отказов некоторых
элементов массового выпуска, когда = ·10-6 ч-1:
- двигатели асинхронные = 8,6;
- двигатели постоянного тока =9,36;
- диоды кремниевые = 0,2;
- изоляторы = 0,0005;
- конденсаторы бумажные = 0,1;
- конденсаторы постоянной емкости = 0,27;
- предохранители = 0,5;
- резисторы проволочные = 0,087;
- резисторы композиционные = 0,053;
- реле электромагнитные = 0,3;
- реле времени пневматические = 3,5;
- транзисторы кремниевые = 0,5;
- тиристоры = 0,45;
- интегральные схемы = 0,75;
- трансформаторы силовые = 1,04.
Приведенные данные могут отличаться в несколько раз
(даже в десять раз) на различных участках сети
железных дорог и от условий эксплуатации.

97.

Самую низкую надежность устройств АТС имеет
напольное оборудование (рельсовые цепи, стрелочные
электроприводы и т.д.) импульсные реле, кабельные и
воздушные линии.
Методы обеспечения надежности систем АТС состоят
в применении высоконадежных, контролепригодных
систем и прогрессивных методов технического
обслуживания.
Современные системы АТС строят на
микропроцессорной и микроэлектронной элементной
базе, поэтому основной метод повышения надежности
состоит во введении избыточности (аппаратной,
временной, информационной, программной), а также
совершенствовании технического обслуживания,
поскольку практически все системы АТС являются
восстанавливаемыми с длительным сроком службы.

98. ГОСТ 27.410-87 установлено 16 видов планов испытаний на надежность. Каждый из них имеет свое обозначение. Буквы U,R,M в обозначениях планов испыта

ГОСТ 27.410-87 установлено 16 видов планов испытаний
на надежность.
Каждый из них имеет свое обозначение. Буквы U,R,M в
обозначениях планов испытаний указывают степень и
характер восстановления объектов:
U- объекты, невосстанавливаемые и незаменяемые при
.
испытаниях в случае отказа;
R – объекты, восстанавливаемые, но заменяемые при
испытаниях в случае отказа;
M – объекты, восстанавливаемые при испытаниях в
случае отказа;
N – объем выборки;
Т- время испытаний или наработки;
r - число отказов или отказавших объектов.

99. Графическое представление планов наблюдений: а - [NUN]; б -[NUT]; в - [NUr]; г - [NRT]; д - [NMr]

100.

101. Расчет показателей надежности при малом числе событий

При большом числе опытов и малой вероятности
события, случайная величина х, принимающая
только целые и неотрицательные значения,
подчиняется распределению Пуассона.
х
а
Px(t)=
ехр( а)
х!
(!)
где - параметр распределения Пуассона.
Распределение Пуассона не только подтверждает
экспоненциальный закон надежности, но и позволяет
аналитически определить вероятность возникновения
одного, двух и более отказов объекта в заданный
отрезок времени.

102.

При стационарном пуассоновском
потоке
отказов
вероятность того, что за время t при интенсивности отказов
= произойдет х событий можно определить по формуле
Px(t)=
t x exp( t )
(!)
x!
Вероятность того, что за время t не произойдет ни одного
события (х =0), т.е. вероятность безотказной работы
Ро(t)=ехр(- t).
Вероятность того, что за время t произойдет одно событие,
(х=1), т.е. один отказ
Q1(t)=( t) ехр(- t),
(!)
Вероятность того, что при тех же условиях в изделии
произойдут 2 отказа, т.е. х=2
Q2(t)=[ ( t)2/2!] ехр(- t);
при х=3
Q3(t)=[ ( t)3/3!] ехр(- t) и т.д.
Ро(t) +∑Qi(t) = 1.
(!)

103.

На практике большое число задач в различных областях
науки и техники решается, используя распределение Пуассона.
Случай 1. Для восстанавливаемых объектов, у которых поток
отказов простейший, промежутки времени между
последовательными отказами имеют экспоненциальное
распределение, наработка на отказ равна Т, случайное число х
отказов за время t распределяется по закону Пуассона с
параметром
=t/Т.
(!)
Случай 2. Если n однотипных невосстанавливаемых объектов
одновременно работают в течение времени t, а наработка до
отказа распределена по экспоненциальному закону с
интенсивностью , то случайное число х отказов объектов за
время t распределено по закону Пуассона с параметром
=n t .
(!)

104.

Пример 1. У восстанавливаемого изделия установился простейший
поток отказов с наработкой на отказ Т= 1000ч. Найти вероятность
того, что у этого изделия будет ровно 1 отказ за 500 ч работы (здесь
α =t/T).
Пример 2. На приемочные испытания ставится 10 изделий из партии.
Испытания продолжаются 100 ч. Партия изделий принимается, если
за время испытаний не происходит отказов. Найти вероятность
приемки партии, если наработка изделия до отказа подчиняется
экспоненциальному закону =10-6ч-1 (здесь α =ntλ).
Пример 3. В объекте одновременно работает
10 однотипных
элементов, имеющих экспоненциальное распределение наработки
до отказа с =10-5 ч-1. Найти вероятность того, что за 1000 ч
работу откажут 3 элемента (здесь α =ntλ).
Пример 4.Найти вероятность того, что при =0,05 случайная
величина, распределенная по закону Пуассона, примет значения: 0;
1;2. Вычислить сумму полученных значений.

105. Расчет норм запасных частей

Запасные части объединяются в комплексы; одиночные
групповые и ремонтные.
Средний расход элементов за время Т
zср = Т/tср = NT .
(!)
Норма одиночного комплекта однотипных запасных
частей
z = zср.
(!)
Параметр зависит от значения вероятности Р(z), т.е.
того, что с вероятностью Р(z) не будет простоев из-за
нехватки элементов данного типа запасных частей.
При Р(z) = 0,95 можно вычислить число запасных
элементов приближенно
z = 5+1,12zср при 20<zср 60..70;
z = 10+1,06 zср при zср 60..70.
(!)
(!)

106.

Значения = z/zср при заданных Р(Z)
Zср
P(Z)
1
2
3
4
5
6
7
25
50
75
100
200
300
400
0,9
1,8 1,65
1,57
1,5
1,47
1,4
1,37
1,24
1,18
1,15
1,12
1,09
1,07
1,06
0,95
2,3 2,0
1,83
1,75
1,67
1,63
1,60
1,33
1,24
1,19
1,16
1,12
1,10
1,09
0,99
3,4 2,65
2,4
2,25
2,05
2,0
1,85
1,47
1,34
1,27
1,23
1,17
1,13
1,12

107.

Пример 1. Установка содержит = 350 однотипных
элементов, имеющих интенсивность отказов =0,86 10-5 1/ч,
должна находиться в эксплуатации Т=2000 ч. Требуется
определить число запасных элементов z для одиночного
комплекта запасных частей при гарантированной
вероятности Р(z)=0,99.
Пример 2. В объекте имеется
=10 однотипных элементов, у
которых средняя наработка до отказа tср=1000ч. Одиночный
комплект запасных частей рассчитывается на период, когда
ожидаемая наработка объекта Т=10000 ч. Задана
вероятность Р(z)=0,95. Найти число элементов одиночного
комплекта запасных частей.

108. Пути повышения надежности сложных систем

Надежность невосстанавливаемой системы Нн
является функцией t, n, i
Нн = (t, n, i ).
Для повышения надежности необходимо:
- упрощать систему (уменьшать число
элементов n);
- уменьшать интенсивность отказов i за счет
выбора более надежных элементов или
облегчения режимов работы элементов;
- сокращать время непрерывной работы
системы t.

109.

Надежность восстанавливаемой системы Нв
является функцией t, n, i , mв
Нв = ( t, n, i , mв).
Для повышения готовности восстанавливаемых
систем добавляются требования повышения ее
ремонтопригодности, в том числе за счет числа
или численности ремонтных бригад и способов
обслуживания системы, т. е. имеется бόльшая
возможность ее сохранения в процессе
эксплуатации.

110.

Надежность системы будет зависеть от объема
избыточности (кратности резервирования К), вида (активный
или пассивный, вр) и способа резервирования (общее или
раздельное, ср). В этом случае функция надежности будет
иметь следующий вид
Н = ( t, n, i , mв,К, вр,ср )
Основная масса дефектов закладывается в изделия еще
на стадии проектирования, а устраняется на стадии
производства или эксплуатации. При этом соотношение
стоимости устранения дефектов на стадии
проектирования, производства и эксплуатации
оценивается как 1; 100; 1000. Это указывает на важность
проработки изделий в ходе их проектирования,
конструирования и подготовки производства.

111. Надежность железнодорожного транспорта

• Под надежностью железнодорожного транспорта
обычно понимают его свойство обеспечивать
своевременную и безопасную доставку грузов и
пассажиров к месту назначения.
• Это свойство имеет большое значение с
экономической точки зрения, поскольку задержка
поездов, нарушение графиков их движения из-за
возможных отказов приводят к существенным
материальным потерям.
• Еще большие потери возникают , если в результате
опасных отказов происходят аварии и крушения
поездов, связанных с ущерба здоровью и жизни
людей, повреждением грузов.

112.

В 2010 г. утверждена КОНЦЕПЦИЯ комплексного управления
надежностью, рисками, стоимостью жизненного цикла
железнодорожного транспорта.
Цель – сокращение стоимости жизненного цикла инфраструктуры и
подвижного состава при условии обеспечения высокого уровня
надежности технических средств и требуемого уровня безопасности
перевозочного процесса.
Целевые показатели безотказности системы определяются согласно
категориям отказов, изложенных в таблице

113.

В основу управления безопасностью перевозочного процесса
положены следующие постулаты:
- абсолютной безопасности не существует;
- в отношении рисков, связанных с жизнью и здоровьем
людей, животных, экологической безопасностью следует при
принятии защитных мер отдавать им приоритет по сравнению
с коммерческими интересами ОАО «РЖД».
Опасные отказы объектов железнодорожного транспорта
возникают на несколько порядков реже отказов его составных
технических средств.
Вероятность безотказной работы в отношении отказов,
угрожающих безопасности движения, должны оставлять не
менее 0,99999.
Экспериментально подтверждается на уровне 0,9-0,999.

114.

Факторы, влияющие на надежность и безопасность железнодорожного
транспорта
К систематическим отказам относятся: ошибки в требованиях;
несоответствие разработки и реализации; недостатки изготовления;
внутренний дефект; ошибки в программировании; ошибки в инструкциях
операторов; организационные ошибки; ошибки человека.
К случайным отказам относятся: ошибки эксплуатации; окружающая
среда; деградация из-за нагрузки; износ, перегрузки.