Методы обработки измерительной информации

1.

*
Методы обработки измерительной
информации

2.

* Методические указания и файлы с данными
доступны по ссылке:
* https://yadi.sk/d/XIBB-7wMvQtvx
* Задача — написать программу на любом
языке программирования, реализующую
описанные в методичке алгоритмы и
применяющую их к массиву данных.
* Языки (среды) для создания программы:
- MatLab
- Scilab(как бесплатный аналог MatLab
- языки программирования – Си, Python и пр.

3.

*
* 1. Титульный лист (по шаблону «Индивидуальное
домашнее задание»)
* 2. Листинг исходного кода программы
* 3. Результаты работы программы, полученные графики:
- проверка по критерию Пирсона
- проверка по критерию Колмогорова
- корреляционная функция случайного процесса
- эргодичность стационарного процесса
* Вывод

4.

*
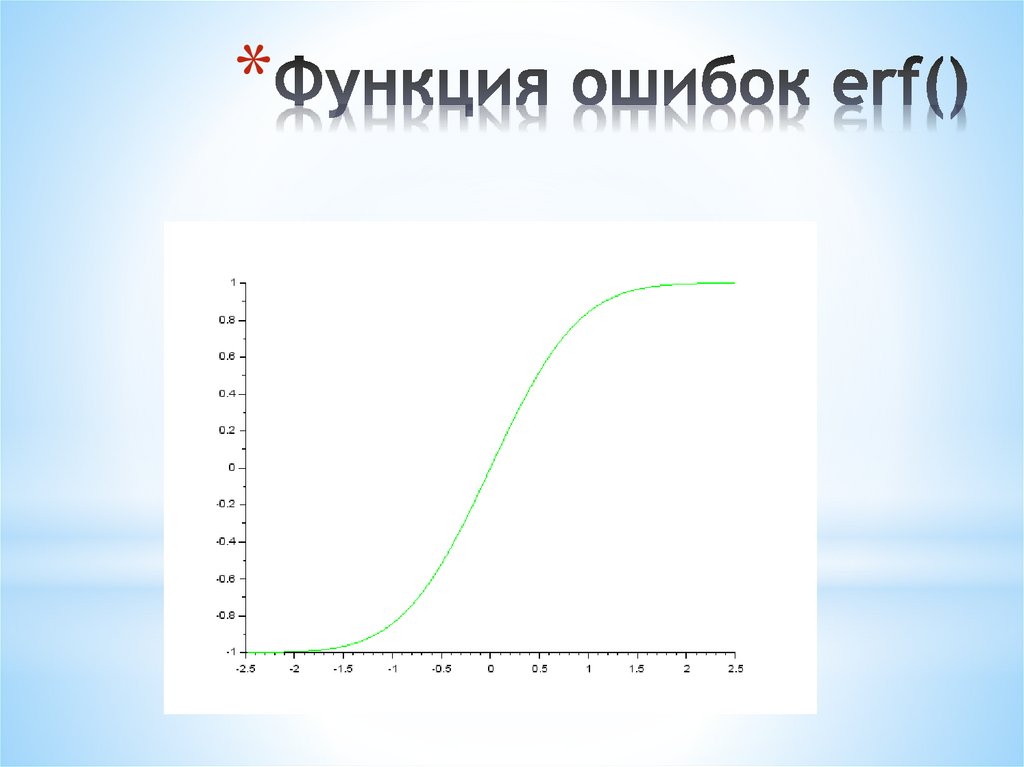
* Функция Лапласа
В разделе 1 методических указаний, функция Φ0(x) ошибочно упоминается как
«функция Лапласа».
На самом деле это нормальное интегральное распределение.
Для расчёта значения Φ0(x) в MatLab нужно использовать не erf(x) (т.е., собственно,
функцию Лапласа), а 0.5*erf(x/sqrt(2)) , т.е. предварительно разделить аргумент на
корень из 2, и разделить значение функции на 2.
Другой, более простой вариант — использовать normcdf(x) - 0.5.
Нормальное интегральное распределение:
Обозначается Ф(x). В аналитической формуле квадрат аргумента делится на 2.
В MatLab вычисляется функцией normcdf().

5.

* Чтобы определить, является ли измерение промахом (в
предположении, что набор измерений распределён нормально):
* 1. Центруем измерение (т.е. вычитаем из него МО).
2. Масштабируем его (т.е. делим на выборочное СКО).
3. Делим на корень из двух.
4. Подставляем в функцию Лапласа (т.е. функцию ошибок).
5. Вычитаем результат из 1.
6. Получившаяся разность — это вероятность ошибиться, назвав
измерение промахом (вероятность ошибки первого рода, т.е.
ложной тревоги).
* Если эта разность меньше принятой величины, которую называют
уровнем значимости (обычно 0.05 или 0.01), то измерение
считается промахом.

6.

* Авторы методических указаний (видимо, под рукой не было таблицы
значений функции Лапласа) решил пересчитать эту формулу в другой вид,
при использовании которого можно было бы вместо функции ошибок
пользоваться нормальным интегральным распределением.
При пересчёте он:
1. Воспользовался тем фактом, что Ф(x) = 0.5 * (1 + erf(x / sqrt(2))).
2. Добавил корректировку поправки Бесселя, т.е. домножил аргумент на
корень из n/(n-1), чтобы конвертировать подправленное (несмещённое)
СКО (вычисленное по формуле 1.1) в выборочное СКО, которое нужно для
фильтрации промахов.
3. Разделил обе части неравенства на 2, в результате чего предлагается
сравнивать Pmax и Pmin не с уровнем значимости, а с уровнем значимости
делённым на 2.
4. Ошибся (опечатался?), в результате чего в формулах для Pmax и Pmin
откуда-то появился множитель n (которого там быть не должно).
Вероятно, лучше вообще не обращать внимания на формулы, приведённые
в п.1 методических указаний, и вместо этого вычислять Pmax и Pmin при
помощи функции Лапласа.
В первом пункте методических указаний, на стр. 6, написано
«Для каждой выборки приведённые вычисления продолжаются до тех пор,
пока значения pmax и pmin, вычисленные для xmax и xmin, не станут
меньше или равными q/2.»
Они, конечно же, должны стать больше. Если они меньше — то это как раз
и есть признак промаха.

7.

*
* fname = uigetfile(["*.txt";"*.txt";"*.txt*"]);
dirs = fileparts(fname); chdir(dirs)
//Чтение файла
M = csvRead(fname, ";");
S = length(M)
Sdl=S/6
for j=1:1:Sdl
Time(j) = j;
A(j)=M(j)
B(j)=M(j+Sdl)
C(j)=M(j+Sdl*2)
D(j)=M(j+Sdl*3)
E(j)=M(j+Sdl*4)
end
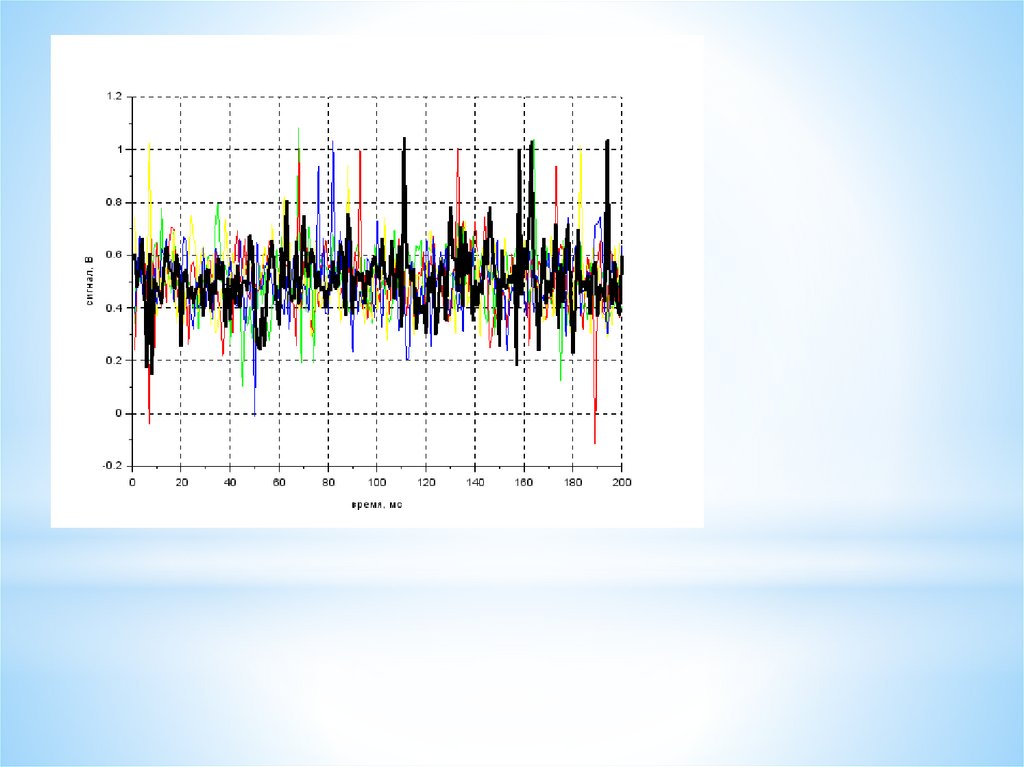
scf()
plot2d(Time, A, color("green")) plot2d(Time, B, color("red")) plot2d(Time, C, color("yellow"))
plot2d(Time, D, color("blue")) plot2d(Time, E, color("black"))
[maxv,pos] = max(A);
av=mean(A);
A1=A-av;
A2=A1/stdev(A1);
AS=erf(A2/sqrt(2));
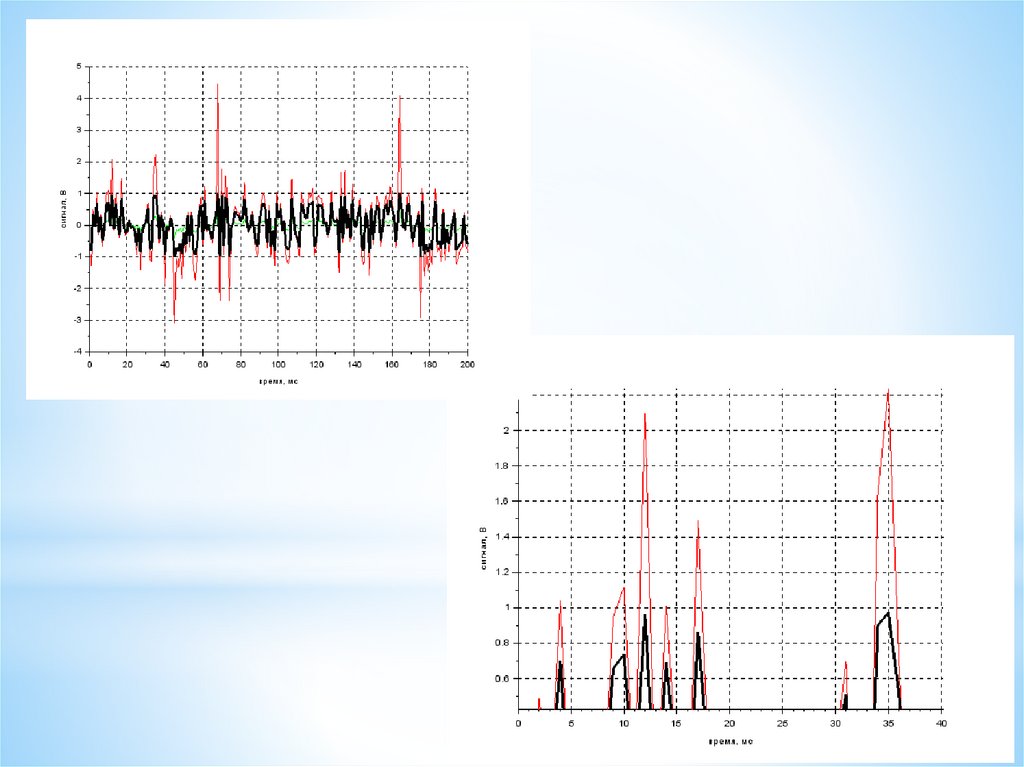
scf()
plot2d(Time, A1, color("green")) plot2d(Time, A2, color("red")) plot2d(Time, AS, color("black")) for
i=1:1:200
x(i)=(i-100)/40;
f(i)=erf(x(i));
end
scf()
plot2d(x, f, color("green"))

8.

9.

10.

*