Активация ядер нейтронами

1.

Учреждение образования
«Международный государственный экологический
университет им. А.Д. Сахарова» БГУ
Факультет мониторинга окружающей
среды
Нейтронная физика
Специальность 1-100 01 01
Ядерная и радиационная безопасность
Кафедра ядерной и радиационной безопасности
2023 - 2024 уч. г.

2.

3.

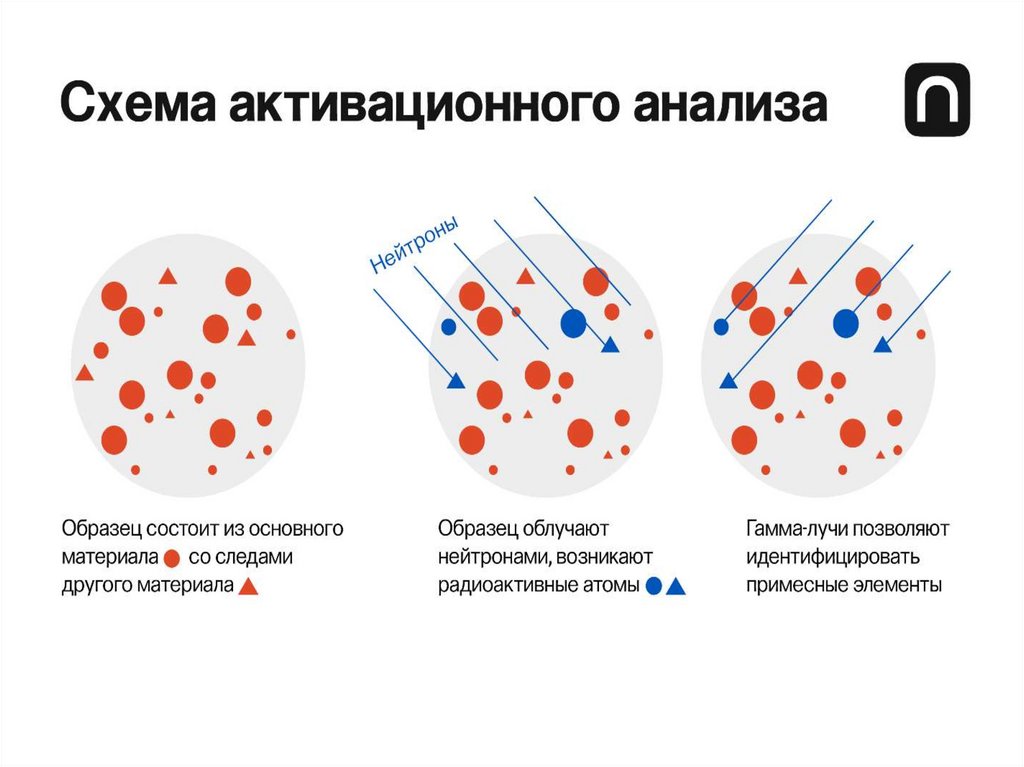
Активационный анализ
- метод определения качественного и количественного состава вещества,
основанный на активации атомных ядер и измерении их радиоактивного
излучения.
• Впервые применен венгерскими химиками Д. Хевеши и Г. Леви в 1936.
• При проведении активационного анализа исследуемый материал в
течение некоторого времени облучают (активируют) частицами (нейтроны,
протоны, дейтроны, α-частицы и т. д.) или жёсткими γ-лучами, а затем с
помощью специальной аппаратуры определяют вид и активность каждого
из образующихся радиоактивных изотопов.
• Каждый радиоактивный изотоп обладает своими, свойственными только
ему одному, характеристиками:
– периодом полураспада Т1/2 и
– энергией излучения Еизл,
• которые никогда не совпадают с аналогичными характеристиками других
изотопов. Эти характеристики собраны в таблицы.

4.

Активационный анализ
• Поэтому, если определить вид излучения и измерить Еизл и
(или) Т1/2 изотопов, присутствующих в активированном
образце, то по таблицам можно провести их
идентификацию (т.е. установить порядковый номер и
массовое число).
• Ядерные реакции, которые при выбранном способе
активирования приводят к образованию тех или иных
радиоактивных изотопов, обычно хорошо известны, и с их
помощью легко найти, из каких исходных изотопов
образовались обнаруженные в активированном образце
радиоактивные изотопы, т.е. определить исходный состав
исследуемого материала.

5.

№
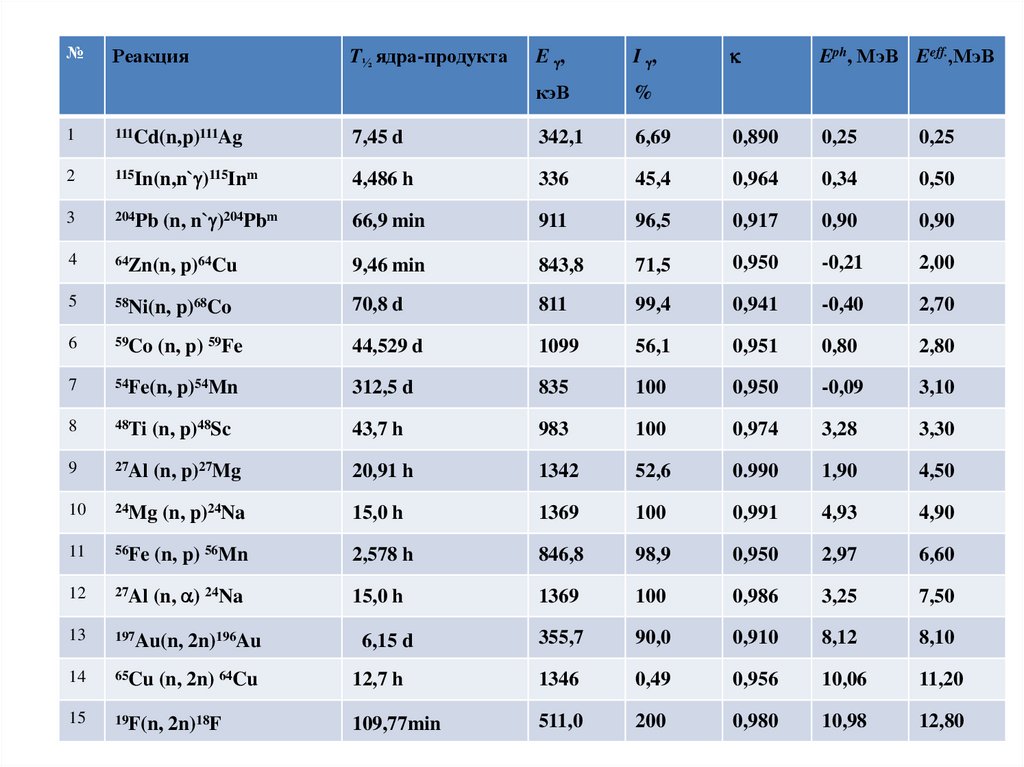
Реакция
T½ ядра-продукта
E ,
I ,
кэВ
%
Eph, МэВ Eeff.,МэВ
1
111Cd(n,p)111Ag
7,45 d
342,1
6,69
0,890
0,25
0,25
2
115In(n,n` )115Inm
4,486 h
336
45,4
0,964
0,34
0,50
3
204Pb (n, n` )204Pbm
66,9 min
911
96,5
0,917
0,90
0,90
4
64Zn(n, p)64Cu
9,46 min
843,8
71,5
0,950
-0,21
2,00
5
58Ni(n, p)68Co
70,8 d
811
99,4
0,941
-0,40
2,70
6
59Co (n, p) 59Fe
44,529 d
1099
56,1
0,951
0,80
2,80
7
54Fe(n, p)54Mn
312,5 d
835
100
0,950
-0,09
3,10
8
48Ti (n, p)48Sc
43,7 h
983
100
0,974
3,28
3,30
9
27Al (n, p)27Mg
20,91 h
1342
52,6
0.990
1,90
4,50
10
24Mg (n, p)24Na
15,0 h
1369
100
0,991
4,93
4,90
11
56Fe (n, p) 56Mn
2,578 h
846,8
98,9
0,950
2,97
6,60
12
27Al (n, ) 24Na
15,0 h
1369
100
0,986
3,25
7,50
13
197Au(n, 2n)196Au
6,15 d
355,7
90,0
0,910
8,12
8,10
14
65Cu (n, 2n) 64Cu
12,7 h
1346
0,49
0,956
10,06
11,20
15
19F(n, 2n)18F
109,77min
511,0
200
0,980
10,98
12,80

6.

7.

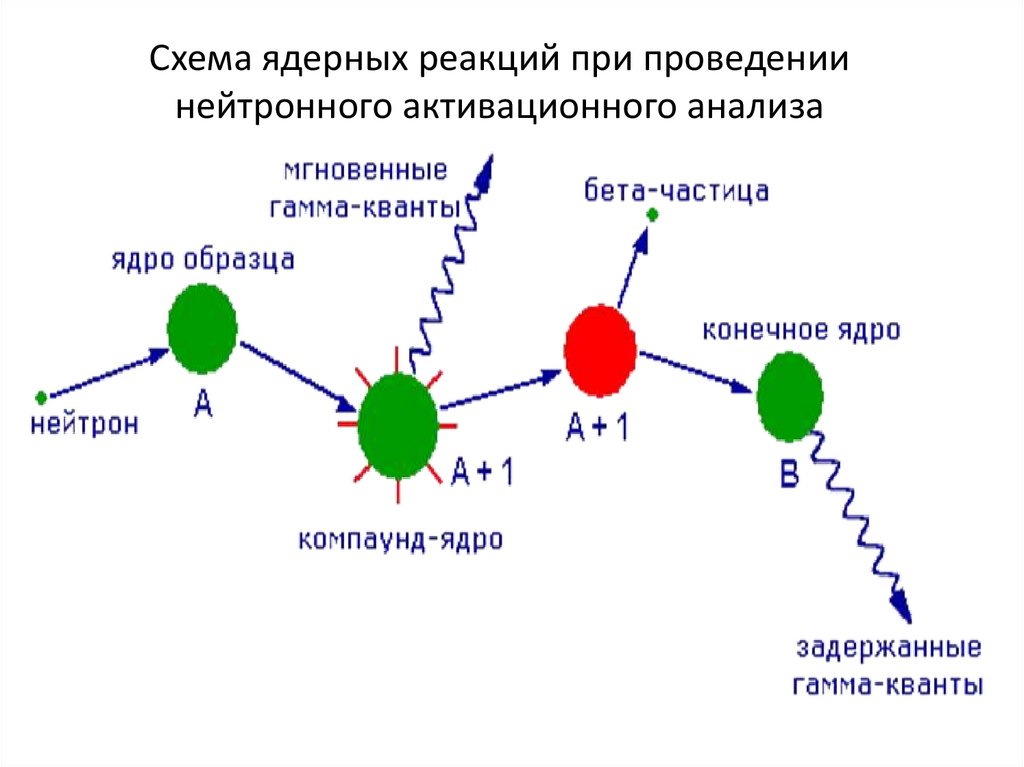
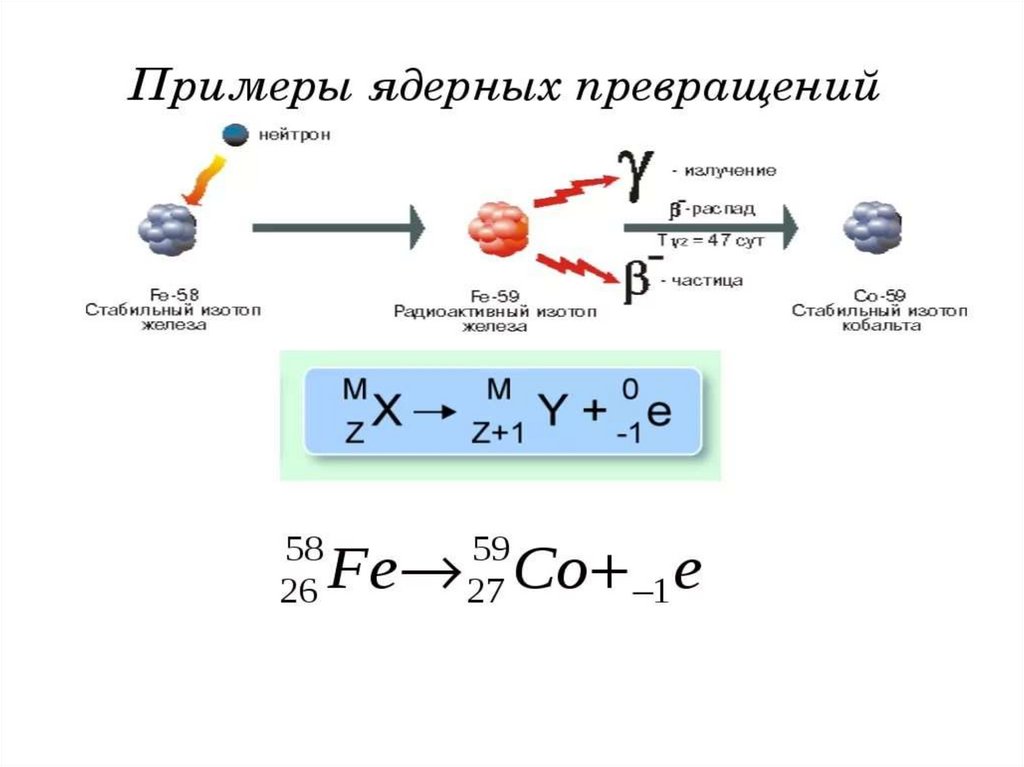
Схема ядерных реакций при проведении
нейтронного активационного анализа

8.

АКТИВАЦИЯ
- процесс получения радиоактивного вещества в результате
ядерных реакций при облучении стабильных ядер
нейтронами, γ-квантами, протонами или другими частицами.
Пусть на образец, содержащий ρ ядер изотопа A падает j
частиц в секунду на единицу площади.
В результате ядерной реакции A(a,b)B за время dt
образовывается
ρ j σi dt ядер радиоактивного изотопа B.
Здесь σi − парциальное сечение данной реакции.
Количество ядер изотопа B определяется соотношением
ρ = mA NA /M,
где mA − масса изотопа A в образце,
M − его молярная масса,
NA − число Авогадро.

9.

АКТИВАЦИЯ
• Образовавшийся изотоп B распадается по закону радиоактивного
распада с постоянной распада λ. Дифференциальное уравнение,
описывающее изменение количества ядер изотопа B, можно
записать в виде
dN = ρ j σi dt – λ N dt
(2)
• Первый член в (2) описывает образование ядер изотопа B, второй −
их распад. Проинтегрировав (2), получим
N(t) = j ρ σi (1 - e –λt )/ λ (3)
• Через некоторое время рост числа активных ядер прекратится
(dN/dt = 0).
• Это произойдет тогда, когда в единицу времени будет
образовываться столько же радиоактивных ядер сколько и
распадаться.

10.

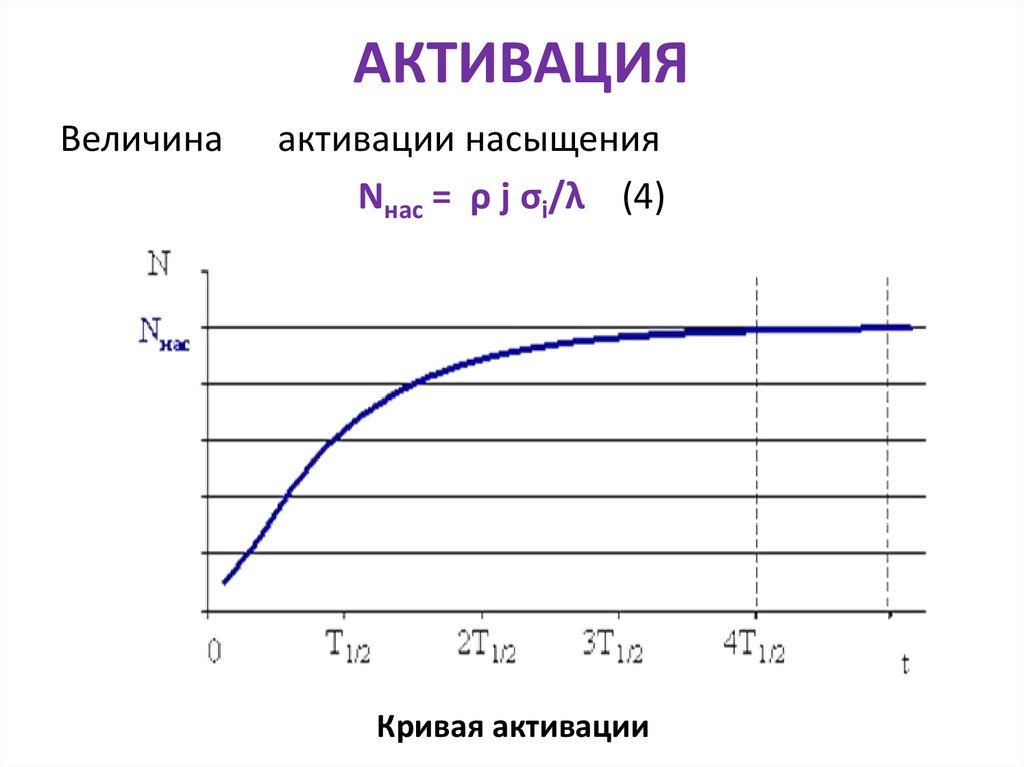
АКТИВАЦИЯ
Величина
активации насыщения
Nнас = ρ j σi/λ (4)
Кривая активации

11.

АКТИВАЦИЯ
• Практически, насыщение достигается за время облучения,
соответствующее 4 - 5 периодам полураспада.
• В самом начале облучения (t << 1/λ) происходит
преимущественно образование изотопа B и его распадом
можно пренебречь, поэтому число активных ядер нарастает
практически линейно со временем.
• После окончания облучения образовавшийся радиоактивный
изотоп B будет только распадаться. Активность I = N, при
постоянной плотности потока j и если пренебречь как правило
ничтожным "выгоранием" (уменьшением числа ядер n), будет
равна
I = I j σi (1 – exp(-λ tобл )) exp (-λ tохл)
(5)
• где tобл − время облучения, tохл − время охлаждения, т.е. время
с момента окончания облучения до момента начала
измерения.

12.

13.

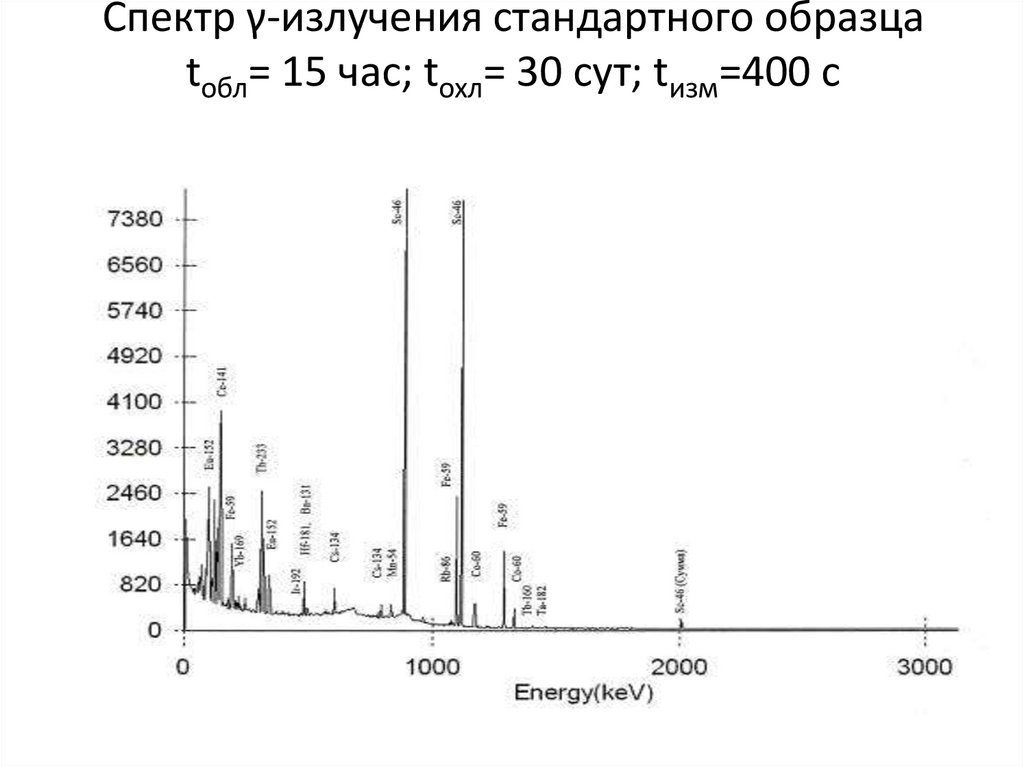
Спектр γ-излучения стандартного образца
tобл= 15 час; tохл= 30 сут; tизм=400 с

14.

АКТИВАЦИОННЫЙ АНАЛИЗ
• На активации основан мощный метод
определения
состава
вещества
активационный анализ.
• Впервые предложен Г. Хевеши и Х. Леви (1936).
• В этом методе идентификация химических
элементов, содержащихся в образце и их
количественный анализ производятся:
• - путем измерения активности,
• - энергии излучений и
• - периода полураспада образовавшихся в
результате ядерной реакции радионуклидов.

15.

АКТИВАЦИОННЫЙ АНАЛИЗ
• Пусть в естественной смеси элемента доля
изотопа A, который в результате реакции A(a,b)B
превращается в радиоактивный изотоп B, равна k.
• Идентифицировав в облученном образце по
периоду полураспада и энергии излучения наличие
изотопа B, по его активности можно определить
массу соответствующего элемента m по формуле
m = ρ M / k NA
(6)
• где М − атомная масса определяемого элемента,
• ρ определяется по активности I (5) изотопа B.
Подставив (5) в (6), получим

16.

АКТИВАЦИОННЫЙ АНАЛИЗ
m = M I exp (λ tохл ) / {k σi j NA (1- exp (-λ tобл)} (7)
Наряду с абсолютным методом, основанным на соотношении (7)
часто применяется относительный метод, при котором активность
образца сравнивается с активностью эталона, содержащего
известное количество определяемого элемента и облученного в
идентичных условиях с образцом (применяется чаще).
В активационном анализе чаще всего используются нейтроны
(нейтронно-активационный анализ) и гамма-кванты (гаммаактивационный анализ).
В качестве источника нейтронов используются:
Радиоизотопные (ампульные) источники
Ядерные реакторы
Нейтронные генераторы.

17.

Активационный анализ
• Пример: определение с помощью нейтронного
активационный анализ процентного содержания
марганца в алюминиевом сплаве.
• Природный марганец состоит только из одного
изотопа 56Mn, а алюминий — только из изотопа 27Al.
• При облучении нейтронами эти изотопы дают
соответственно β-активные 57Mn с Т1/2 = 2,58 ч. и 28Al с
Т1/2 = 2,3 мин.
• Из-за малости Т1/2 28Al практически нацело распадается
через 15—20 мин после прекращения облучения, и
активность сплава будет определяться присутствием в
нём 57Mn.

18.

19.

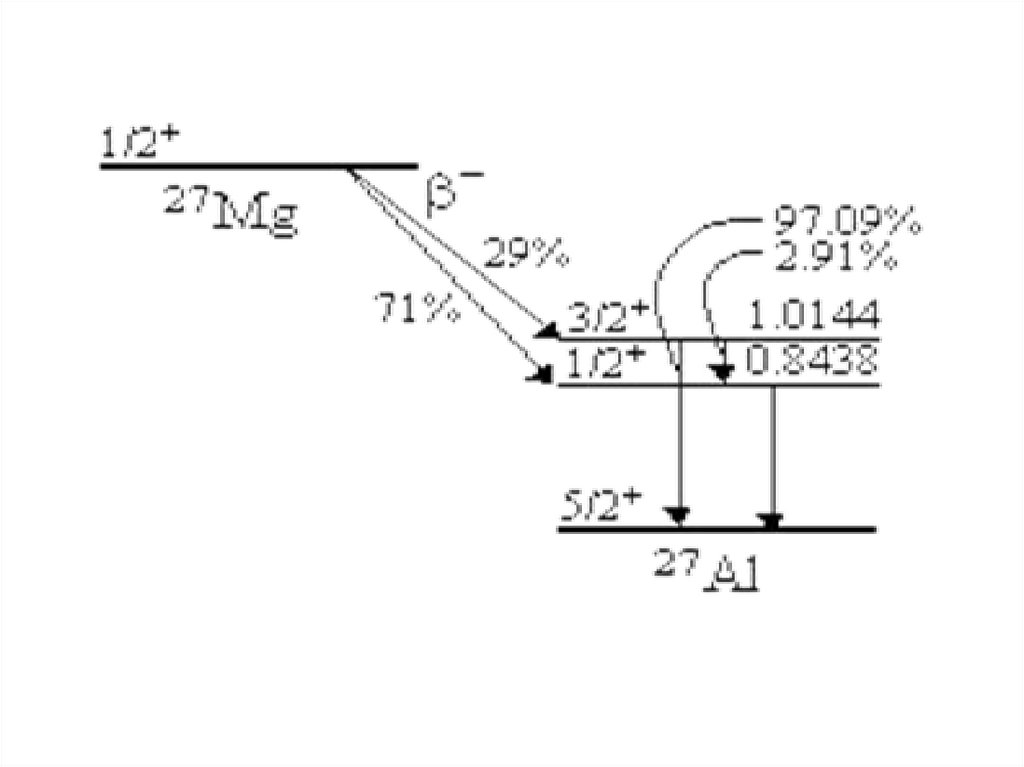
Изотопом магния, который служит для анализа,
является 26Mg (содержание в естественной смеси 11.01%).
Получающийся в результате реакции 26Mg(n,γ)27Mg с
сечением 0.0372 барн β-радиоактивный изотоп 27Mg
имеет период полураспада 9.458 минут.
Он распадается на возбужденные состояния 27Al, которые
сбрасывают энергию возбуждения эмиссией γ-квантов.
γ-кванты, которые служат для идентификации и
количественного анализа имеют энергии E1 = 1.0144 МэВ и
E2 = 0.8438 МэВ.
Приблизительно 71% всех β-распадов сопровождается
испусканием γ-квантов с энергией E1 ~28% и с энергией E2.
При анализе необходимо учесть эффективность
регистрации γ-кантов соответствующих энергий.

20.

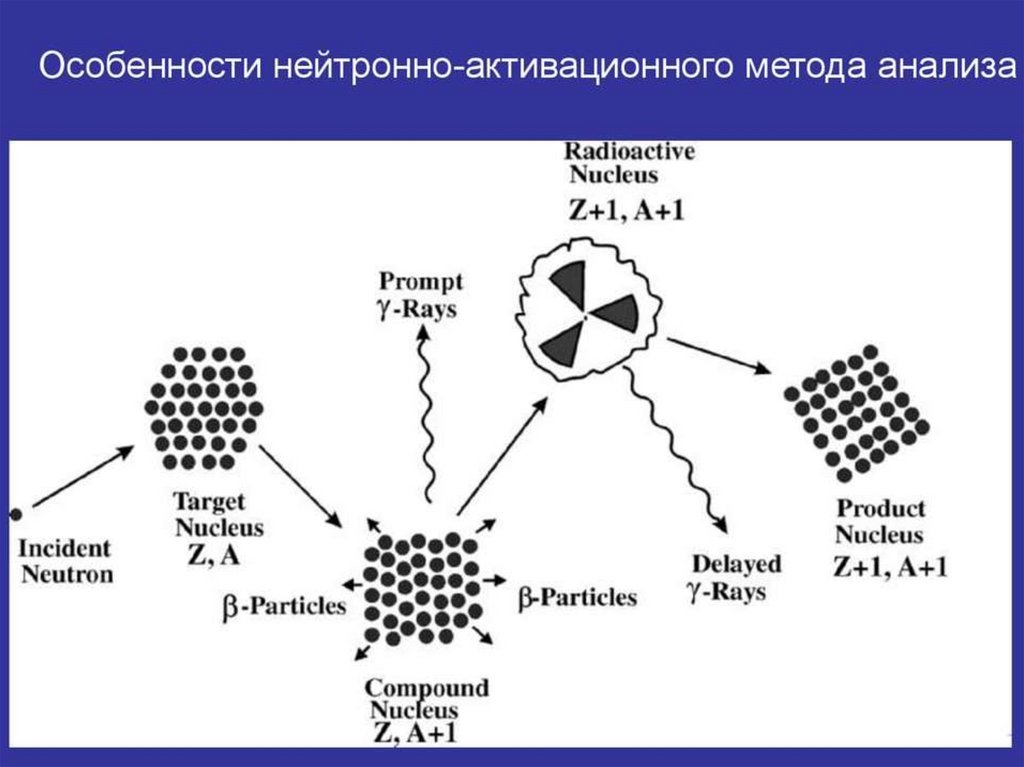
Нейтронно-активационный анализ
• В принципе нейтронно-активационный анализ
возможен на:
– мгновенных гамма-квантах (1), когда измерения
проводятся в процессе облучения, или
– на задержанных гамма-квантах (2), когда измерения
проводятся во время бета-распада.
• Первый метод обычно реализуется на выведенном
из реакторе пучке нейтронов.
• При этом потоки, падающие на образец на ~6
порядков меньше, чем при облучении внутри
реактора. Зато детектор может быть расположен
очень близко к образцу.

21.

Нейтронно-активационный анализ
• Этот метод в основном применим для
– элементов с экстремально большим сечением
реакции радиационного захвата (B, Cd, Sm и Gd);
– элементов, изотопы которых имеют малые
периоды полураспада, чтобы можно было
использовать второй метод,
– Элементов, у которых в результате реакции (n,γ)
образуются только стабильные изотопы или
– Элементов, у которых аналитические изотопы
испускают
гамма-кванты
с
малой
интенсивностью.

22.

АКТИВАЦИОННЫЙ АНАЛИЗ
• Около 70% элементов имеют свойства, позволяющие
использование нейтронно-активационного анализа для их
идентификации и количественного анализа.
• Для γ-активационного анализа используется тормозное
излучение высокой интенсивности (1014-1015 квант/с),
получаемое на электронных ускорителях.
• Фотоядерные реакции позволяют активировать практически
все элементы периодической системы элементов с пределом
обнаружения ~10-4-10-7%.
• Существуют
ситуации,
когда
использование
гаммаактивационного анализа предпочтительно.
• γ-активационный анализ в частности позволяет эффективно
анализировать такие элементы, как Ca, Ni, Ti, Tl и Pb.

23.

АКТИВАЦИОННЫЙ АНАЛИЗ
• Преимуществом γ-активационного анализа перед
нейтронно-активационным анализом является также то,
что гамма-кванты могут глубже проникать в образец,
следовательно анализу могут подвергаться образцы
бо'льших размеров.
• Активационный анализ на заряженных частицах, в связи с
их малыми пробегами в веществе, используется главным
образом для анализа тонких слоев и поверхностей.

24.

25.

Инструментальный и радиохимический
анализ
• Облучение исследуемых проб приводит к образованию
смеси радионуклидов различных химических элементов,
входящих в пробу.
• Идентификацию отдельных радионуклидов осуществляют:
– либо по их ядерно-физическим свойствам (энергия и вид
испускаемых частиц, период полураспада), применяя для этих
целей
счетчики
гамма-квантов
и
β-частиц
и
гамма-
спектрометры,
– либо измеряя активность радионуклида в течение какого-то
времени для установления его периода полураспада.
• Данные об интенсивности отдельных видов излучения,
принадлежность которых установлена, используют для
расчета содержания элементов в исследуемой пробе

26.

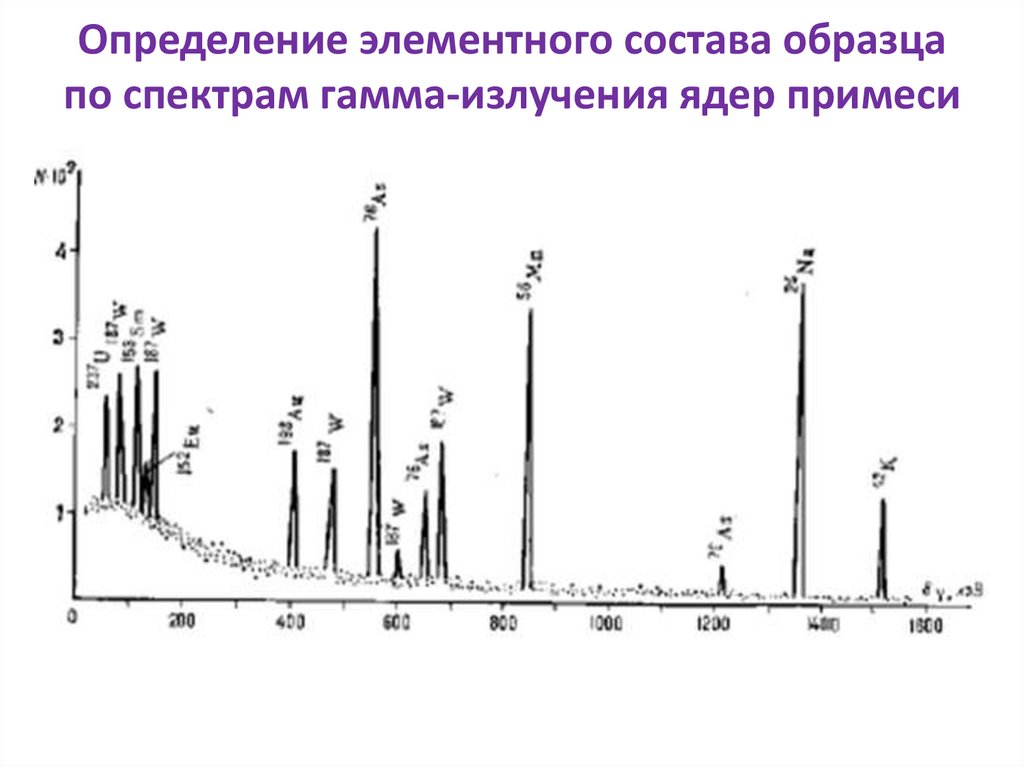
Определение элементного состава образца
по спектрам гамма-излучения ядер примеси

27.

Нейтронно-активационный анализ
• Количество зарегистрированных в процессе анализа
импульсов с учетом уменьшения активности во время
измерения выражается следующим соотношением:
где mx — масса определяемого элемента в пробе,
Y — относительная распространенность изотопа,
ν — квантовый выход излучения,
ε — эффективность регистрации излучения данного вида,
tизм — время измерения.

28.

Нейтронно-активационный анализ
• Если период полураспада радионуклида достаточно велик,
т.е.
то :
• где Aвыд — активность определяемого нуклида после выдержки;
–
tвыд — время между концом облучения и началом
измерения активности.
• Используя оба выражения, по измеренным значениям
ΔА вычисляют содержание исследуемого элемента mx в пробе.
• Из последнего уравнения следует, что с увеличением периода
полураспада уменьшается число полезных зарегистрированных
сигналов.
• Следовательно, экспрессность анализа будет выше при анализе
проб по короткоживущим радионуклидам.

29.

Нейтронно-активационный анализ
• Приведенный метод определения содержания элемента по
активности накопившегося радионуклида без привлечения
эталона называется абсолютным методом.
• Однако в этом случае необходимо знать плотность потока и
энергию бомбардирующих частиц.
• Например, при облучении проб реакторными нейтронами
требуются данные о плотности потока и энергетическом спектре
нейтронов, а также информация о величинах резонансных
интегралов для облучаемых нуклидов, поскольку одни нуклиды
(например, 23Na, 45Sc, 58Fe, 139La) преимущественно активируются
тепловыми
нейтронами,
а
другие
(75As, 87Br, 121,123Sb, 181Ta, 197Au, 113,115In) и тепловыми, и
резонансными нейтронами.
• Важным требованием в абсолютном методе является
соблюдение постоянства потока активирующего излучения во
времени. Необходимо также обеспечить измерение абсолютной
активности накопившегося радионуклида с достаточной
точностью.

30.

Относительный метод
• Одновременно с анализируемой пробой облучается эталон с точно
известным количеством определяемого элемента. Наведенные
активности эталона и пробы измеряют в одинаковых условиях, а
содержание определяемого элемента вычисляют из соотношения
• где mx и mэ — масса элемента в пробе и эталоне;
• Ах и Аэ — активность пробы и эталона, соответственно.
• Такое
исследование
без
разрушения
образцов
называют инструментальным активационным анализом.
• Если же при облучении пробы получается сложная смесь
радионуклидов и ее невозможно расшифровать из-за совпадения
или наложения близких по энергии γ-квантов, то облученную пробу
растворяют, проводят радиохимически чистое выделение
отдельных элементов или группы элементов и затем по
измеренной активности радионуклидов рассчитывают содержание
элементов.
• Такой вариант называется активационным анализом с
радиохимическим разделением.

31.

НЕЙТРОННО-АКТИВАЦИОННЫЙ АНАЛИЗ
• В соответствии с энергиями нейтронов
различают три вида ННА:
– НАА на тепловых нейтронах,
– НАА на промежуточных нейтронах,
– НАА на быстрых нейтронах.
• Каждый вид имеет свои достоинства и
недостатки.

32.

33.

34.

Литература
• Ваганов П.А., Лукницкий В.А. Нейтроны и
криминалистика. — Л.: ЛГУ, 1981. — 192 с.
• Кузнецов Р.А. Активационный анализ. — М.,
1974. — 343 с.
• Маслов И.А., Лукницкий В.А. Справочник по
нейтронному активационному анализу. — Л.,
1971. — 312 с.
• Мир-Бабаев М.Ф. Микроэлементный состав
нефтей по данным нейтронно-активационного
анализа // "Химия и технология топлив и
масел", 1997, №5, с.46-47.

35.

Радиоизотопные источники нейтронов
• В радиоизотопных источниках используются нейтроны
спонтанного деления (252Cf) или реакции типа (α,n) и (γ,n).
• 1 миллиграм 252Cf испускает 2.28·109 нейтронов в секунду с
энергией 1.5 МэВ.
• Нейтронный источник, использующий реакции (α,n), должен
содержать α-источник и легкий изотоп (Li, Be, B) на котором
происходит реакция (α,n). Использование легких изотопов
связано с тем, что энергия α-частиц должна быть больше
высоты кулоновского барьера.
• В противном случае сечение реакции будет сильно
подавлено. Например, в
Pu/Be источнике используется
смесь металлического порошка Ве с небольшим количеством
α-излучателя - полония. Нейтроны образуются в
реакции 9Be(α,n)12C (практически сплошной спектр от 0 до 13
МэВ.

36.

Радиоизотопные источники нейтронов
• Источником нейтронов, основанным на фотоядерной
реакции, является смесь радия и бериллия.
• В этом случае источник нейтронов представляет собой
систему из двух запаянных ампул. Внутри ампулы с
порошком бериллия помещается ампула с солями радия
таким образом, что на бериллий действует только гаммаизлучение, проходящее через стенки внутренней ампулы.
• Нейтроны образуются в реакции 9Ве(γ,n)8Ве. Такой источник
испускает монохроматические нейтроны с энергией 110 кэВ.
• Интенсивность
радиоизотопных
источников
106108 нейтронов/c, чувствительность (предел обнаружения)
элементов ~10-4-10-6%.

37.

ЯДЕРНЫЕ РЕАКТОРЫ
• являются мощными источниками нейтронов.
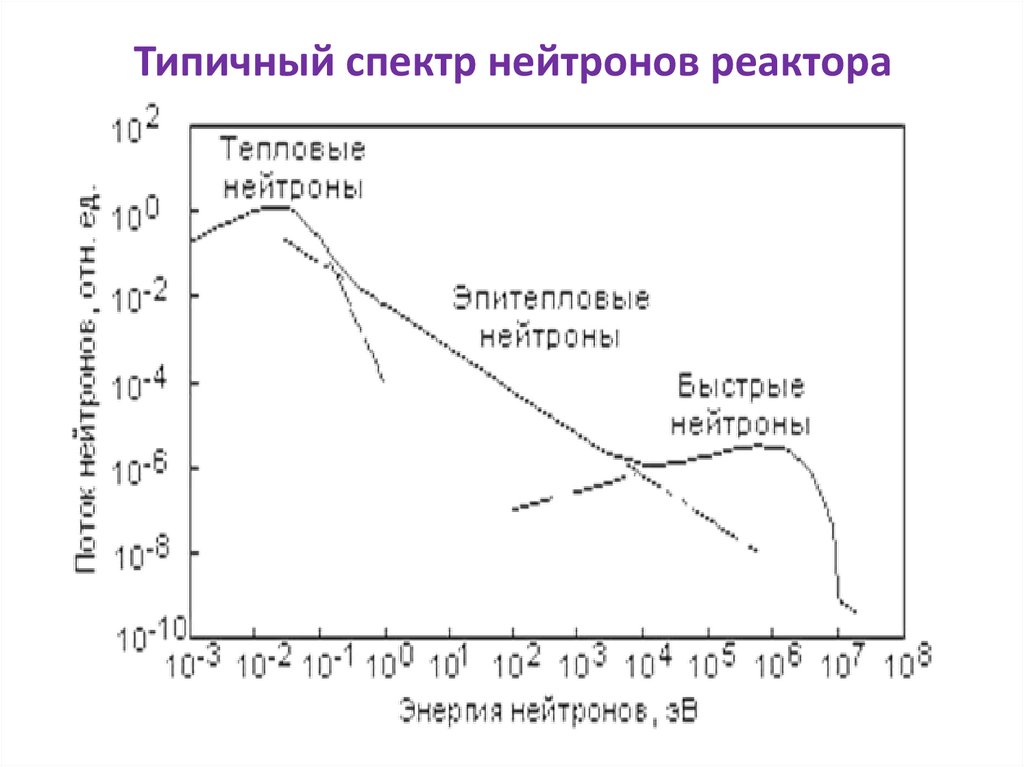
• Спектр нейтронов очень широк. В нем выделяют 3 компоненты
- тепловые, эпитепловые (резонансные) и быстрые нейтроны.
• Тепловые нейтроны это нейтроны с энергией < 0.5 эВ. Они
находятся в тепловом равновесии с атомами материала
реактора.
• При комнатной температуре они имеют энергетическое
распределение Максвелла-Больцмана со средней энергией
0.025 эВ и наиболее вероятной скоростью 2200 м/с.
• При облучении образцов как правило 90-95% нейтронного
потока составляют тепловые нейтроны.
• Реактор мощностью 1 МВт обеспечивает нейтронный
поток ~1013 (cм-2с-1).
• Предел
обнаружения
большинства
элементов
при
использовании таких потоков составляет 10-5-10-10%.

38.

ЯДЕРНЫЕ РЕАКТОРЫ
• Эпитепловые нейтроны имеют энергии в диапазоне
от 0.5 эВ до ≈ 0.5 МэВ.
• Их доля в реакторе ≈ 2%.
• Кадмиевая пластинка толщиной 1 мм поглощает все
тепловые нейтроны, но пропускает эпитепловые и
быстрые нейтроны.
• Как тепловые, так и эпитепловые нейтроны
вызывают в мишени реакции (n,γ).
• Доля быстрых нейтронов ( > 0.5 МэВ) в реакторе
составляет ≈5%. Они вызывают реакции (n,p), (n,n') и
(n,2n) и практически не вызывают реакции (n,γ).

39.

Типичный спектр нейтронов реактора

40.

Нейтронные генераторы
• Нейтронные генераторы это ускорители в которых нейтроны
образуются в результате ядерных реакций на соответствующих
мишенях.
• Чаще всего используются реакции
2H(d,n)3He, Q = 3.270 МэВ
(7)
3H(d,n)4He, Q = 17.590 МэВ (8)
• В результате получаются нейтроны с энергиями ≈2.5 МэВ и
≈14.1 МэВ.
• Сечения этих реакций достаточно велики при небольших энергиях
дейтронов, можно обойтись небольшими ускорителями.
Максимум сечения реакции (8) при энергии Td = 120 кэВ.
• Обычно используются каскадные генераторы. Типичный выход
нейтронов у нейтронных генераторов ≈ 1010 c-1.
• Использование быстрых нейтронов позволяет проводить анализ
легких элементов (C, N, O), которые плохо активирующихся
тепловыми нейтронами.

41.

Формула четырех сомножителей
• Коэффициент размножения нейтронов k — отношение
числа нейтронов последующего поколения к числу
нейтронов в предшествующем поколении во всём объеме
размножающей
нейтронной
среды
(активной
зоны ядерного реактора). В общем случае, этот
коэффициент может быть найден с помощью формулы
четырёх сомножителей:
K=μϕθη
Где
K - коэффициент размножения в бесконечной среде;
μ – коэффициент размножения на быстрых нейтронах
ϕ – вероятность избежать резонансный захват
Θ – коэффициент использования тепловых нейтронов
η – выход нейтронов на одно поглощение

42.

Вероятность избежать резонансного захвата ϕ
• — вероятность достижения быстрым нейтроном
тепловой энергии. Данная величина представляет собой
отношение числа быстрых нейтронов, избежавших
захвата во время замедления к числу всех быстрых
нейтронов ϕ <1.
• Как известно, ядро может захватить нейтрон только в том
случае, если кинетическая энергия нейтрона близка к
энергии одного из энергетических уровней нового ядра,
образующегося в результате захвата. Сечение захвата
такого нейтрона ядром резко увеличивается.
• Энергия, при которой сечение взаимодействия нейтрона с
ядром достигает максимума, называется резонансной.
• Резонансный диапазон энергий разбит на две части:
• область разрешенных и
• неразрешенных резонансов.

43.

44.

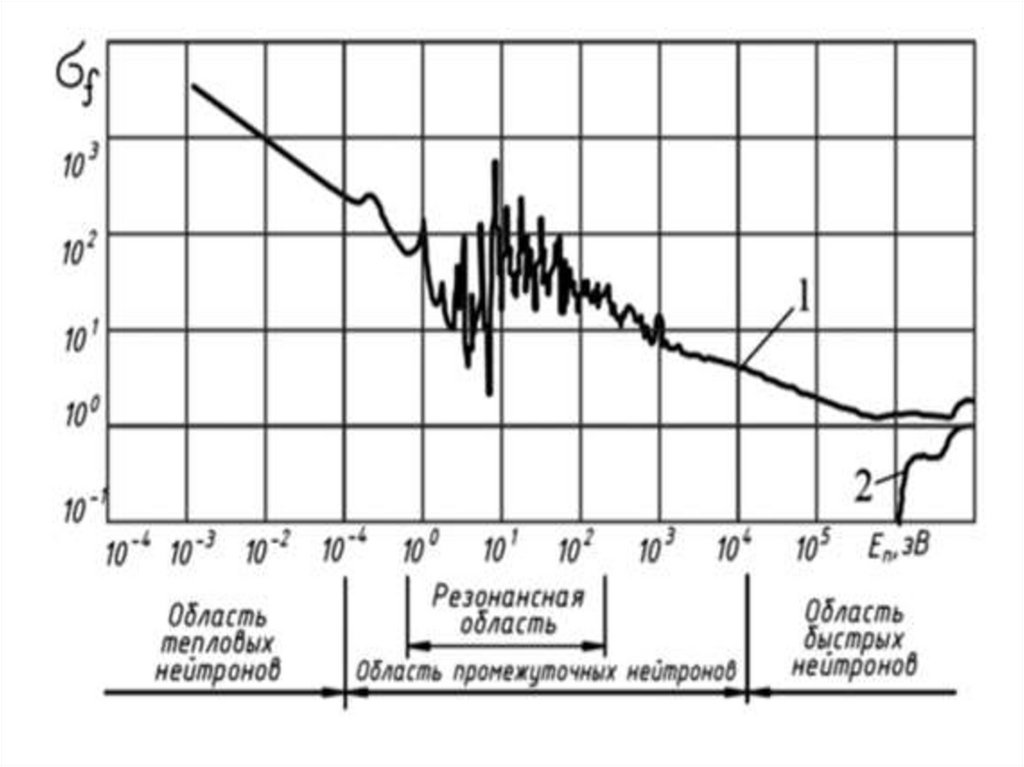
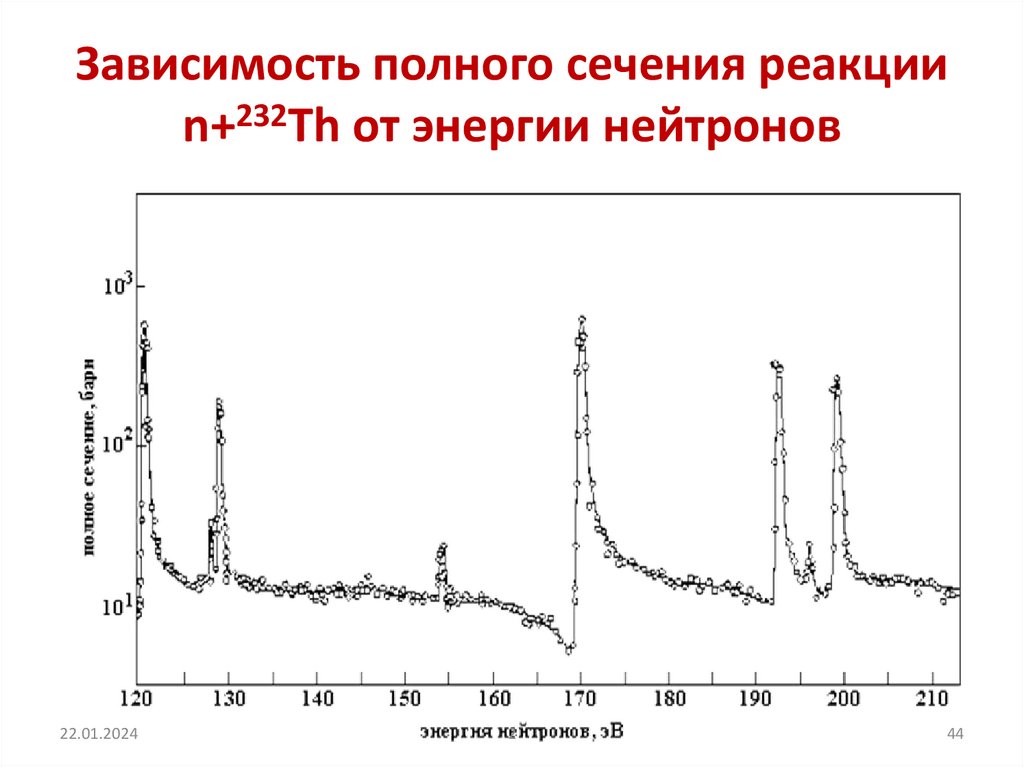
Зависимость полного сечения реакции
n+232Th от энергии нейтронов
22.01.2024
2
44

45.

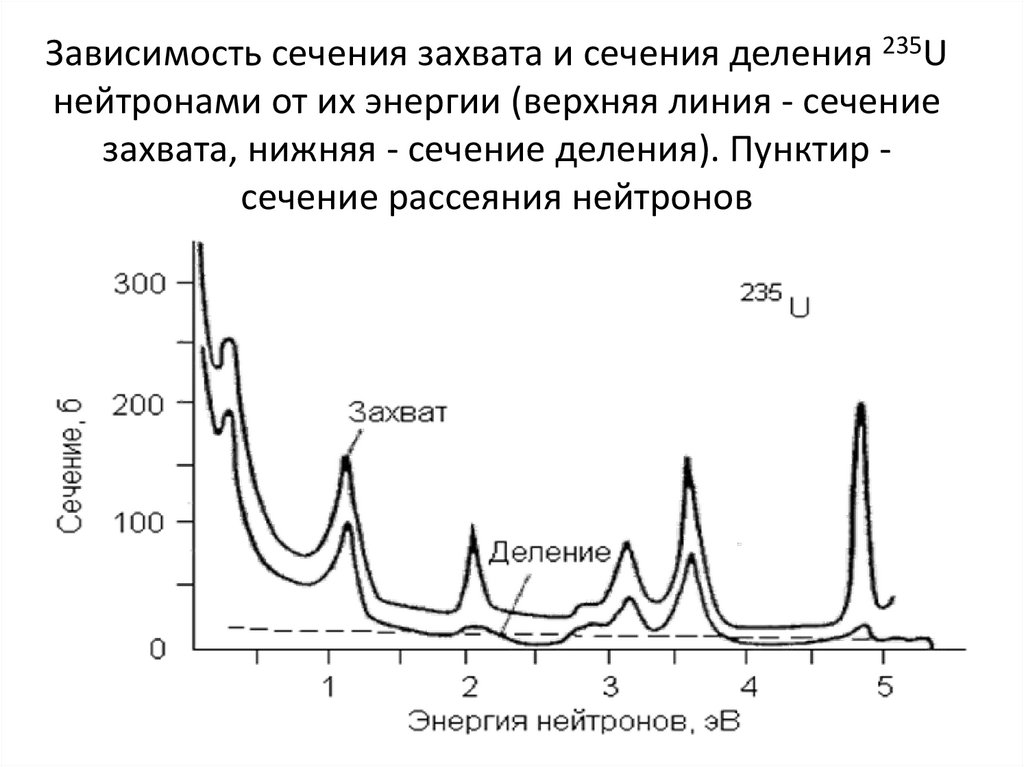
Зависимость сечения захвата и сечения деления 235U
нейтронами от их энергии (верхняя линия - сечение
захвата, нижняя - сечение деления). Пунктир сечение рассеяния нейтронов

46.

Вероятность избежать резонансного захвата ϕ
• Первая область занимает энергетический интервал от
1 эВ до Eгр. В этой области энергетическое разрешение
приборов достаточно для выделения любого резонансного
пика.
• Начиная с энергии Eгр расстояние между резонансными
пиками становится меньше энергетического разрешения и
резонансные пики не разделяются.
• У тяжёлых элементов граничная энергия Eгр≈1 кэВ.
• В реакторах на тепловых нейтронах основным резонансным
поглотителем нейтронов является 238U.
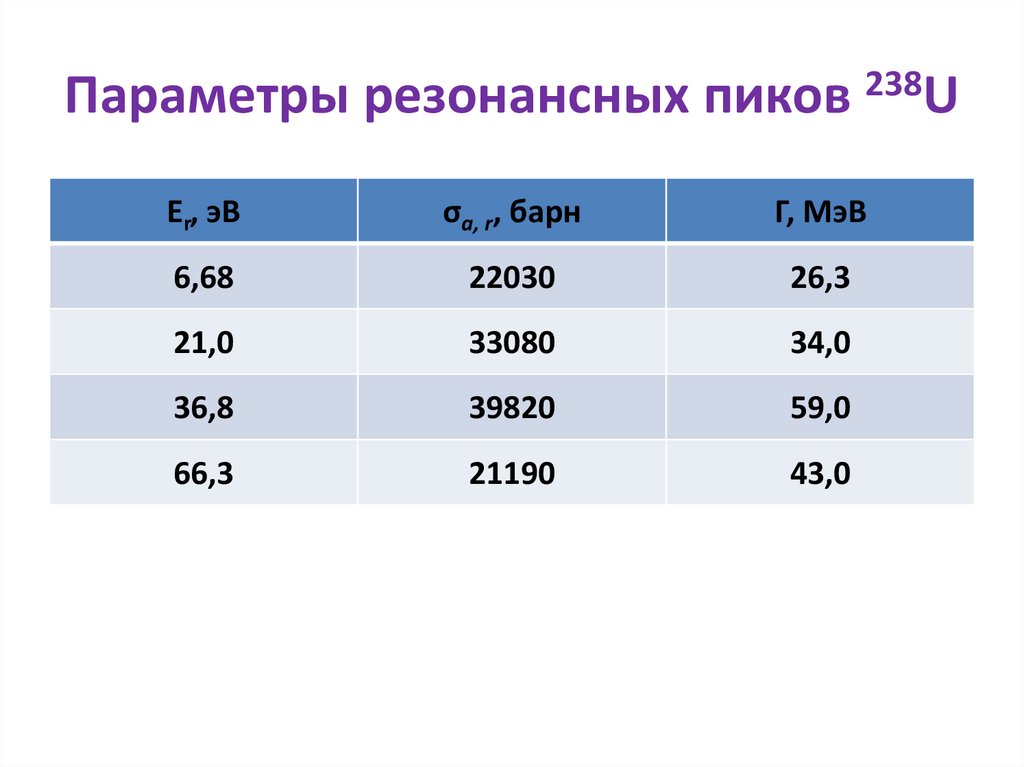
• В таблице для 238U приведены несколько резонансных
энергий нейтронов Er, максимальные сечения поглощения
σa, r в пике и ширина Г этих резонансов.

47.

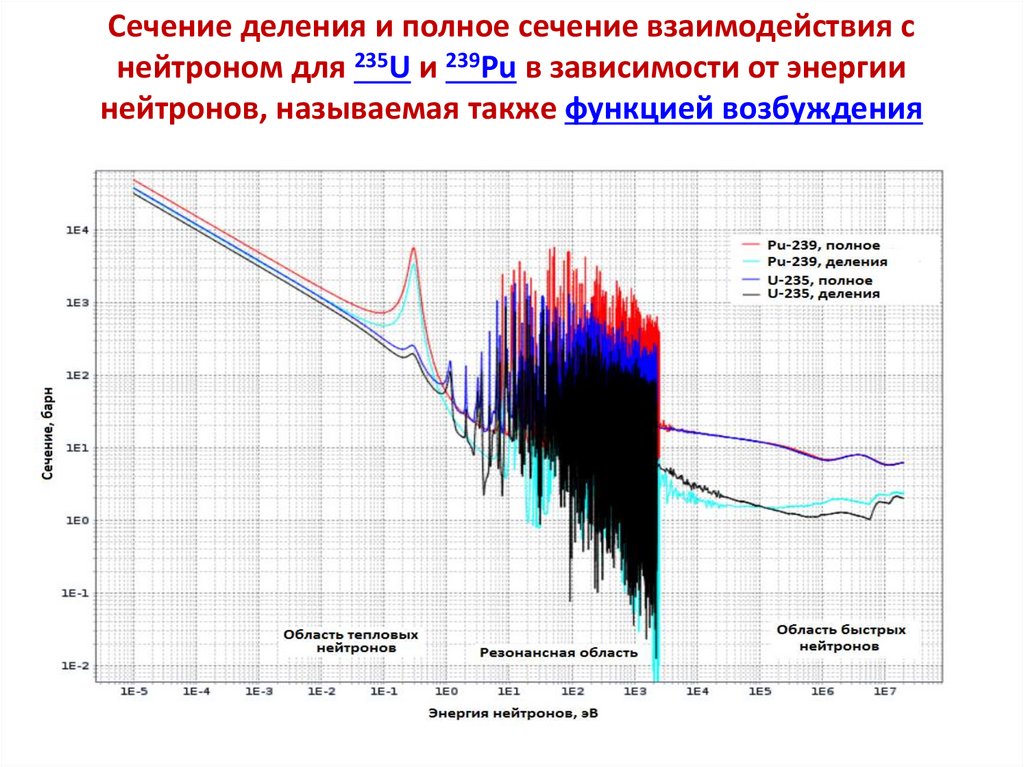
Cечение деления и полное сечение взаимодействия с
нейтроном для 235U и 239Pu в зависимости от энергии
нейтронов, называемая также функцией возбуждения

48.

Параметры резонансных пиков 238U
Er, эВ
σa, r, барн
Г, МэВ
6,68
22030
26,3
21,0
33080
34,0
36,8
39820
59,0
66,3
21190
43,0

49.

Резонансный интеграл
• Рассмотрим задачу о нахождении спектра нейтронов и
вероятности избежать поглощения при замедлении в
среде, состоящей из смеси ядер замедлителя с атомной
массой больше единицы и поглотителя (тяжелые ядра).
• Оказывается, что уравнение замедления в данной
постановке задачи без дополнительных приближений (как
в случае замедления на водороде) решить не
представляется возможным.
• В физике ядерных реакторов большой интерес
представляет вероятность избежать поглощения при
замедлении от Е0 – энергии, при которой нейтроны
рождаются (около 2 МэВ), до Еth – верхней границы
тепловой области энергии (1 – 5 эВ).
• Естественно, что эту вероятность можно рассчитать по
формуле:

50.

Резонансный интеграл
• ϕ(E0, Eth) ≈ exp[- ∫ Σa (E’) dE’ /( ξ Σa (E’) dE’ )]
• Расчет вероятности избежать поглощения при замедлении
по этой формуле, представляет собой сложную задачу.
• Действительно, для каждой конкретной топливной
композиции необходимо вычислить интеграл по
энергетической переменной от функции, которая имеет
сложную (резонансную) зависимость от энергии и которая
стоит и в числителе, и в знаменателе подынтегральной
функции.
• Задача существенно усложняется для реальных сред,
состоящих из нескольких десятков резонансных
поглотителей (тяжелых ядер).
• среднелогарифмическая потеря энергии на одно
столкновение . Для А > 10

51.

Резонансный интеграл
• В показателе экспоненты в выражении стоит интеграл
• R = ∫ Σa (E’) dE’ /( ξ Σa (E’) dE’ ) (от Е0 до Етепл) который
пропорционален скорости поглощения нейтронов.
• Действительно, скорость поглощения нейтронов в области
от E0 до Eth рассчитывается по формуле:
• R1 = ∫ Σa (E’) Ф(E’) dE’
• Перепишем R в переменных летаргии
• R = ∫ Σa (u’) du’ /( ξ Σa (u’) du’ ) от 0 до uth.
• Если во всей области замедления реализуется случай
слабого поглощения, то полное макроскопическое сечение
приблизительно равно макроскопическому сечению
рассеяния замедлителя и не зависит от энергии нейтрона

52.

Резонансный интеграл
• Σtot ≈ Σs замедлителя
• В этом случае выражение для R
• R = ∫ Σa (u’) du’ /( ξ Σs zam (u’) du’ ) =
• = Nпогл ∫ du’ σа(u’)/ ( ξ s zam du’ ) =
• = Nпогл I 1/ (ξ Σs zam )
• I = ∫ du’ σа(u’)
• Nпогл - количество ядер поглотителя.

53.

Резонансный интеграл
• I называется истинным резонансным интегралом и
представляет собой интеграл от микроскопического
сечения поглощения поглотителя по всей области
замедления и измеряется в барнах.
• Истинный резонансный интеграл не зависит от
соотношения ядер поглотителя и замедлителя в
среде, а является характеристикой данного
нуклида.
• Для всех значимых в физике ядерных реакторов
нуклидов
он
рассчитан
и
приведен
в
соответствующих справочниках.

54.

Резонансный интеграл
• Таким образом, если во всей области замедления реализуется
случай слабого поглощения, то вероятность избежать
резонансного захвата может быть рассчитана по формуле:
• ϕ(o, uth) = exp [- Nпогл I / (ξ Σs zam )]
• R = ∫ Σ a (u’) (ξ Σtot (u’) du' = Nпогл / (ξ Σsзам) ∫ du’ σa погл
• I ≡ ∫ du’ σa погл Σs zam / Σtot (u’) - называется эффективным
резонансным интегралом и измеряется в барнах.
• Эффективный резонансный интеграл рассчитывается для
конкретной среды, поскольку он зависит от соотношения ядер
поглотителя и замедлителя в среде, т.е. от изотопного состава
среды.
• Эффективный резонансный интеграл в отличие от истинного
учитывает
резонансную
самоэкранировку,
поскольку
использует спектр Вигнера.

55.

Резонансный интеграл
• Зная эффективный резонансный интеграл в данной
среде, можно рассчитать вероятность избежать
поглощения при замедлении:
• ϕ(E0, Eth) = exp[- Nпогл /( ξ Σs зам)]
• Исходя из последней формулы, легко дать
определение Iэфф .
• Эффективный резонансный интеграл – эффективное
микроскопическое
сечение
поглощения
ядер
резонансного поглотителя, которое позволяет на
невозмущенном спектре замедления [спектре Ферми –
1/ (ξ Σs)] правильно рассчитать интегральную величину
– вероятность избежать поглощения при замедлении.

56.

Эффективный резонансный интеграл
• Полагаем, что резонансные нейтроны движутся в
бесконечной
системе,
состоящей
из замедлителя и 238U.
• При столкновении с ядрами замедлителя нейтроны
рассеиваются, а с ядрами 238U — поглощаются.
Первые столкновения способствуют сохранению и
выведению резонансных нейтронов из опасной
зоны, вторые ведут к их потере.
• Вероятность избежать резонансного захвата
(коэффициент ϕ) связана с плотностью ядер NS и
замедляющей
способностью
среды
ξΣS соотношением
ϕ = exp(-Ns Jeff / ξ Σs)

57.

Эффективный резонансный интеграл
Величину Jeff называют эффективным резонансным
интегралом.
Он характеризует поглощение нейтронов отдельным
ядром в резонансной области и измеряется в барнах.
Использование эффективного резонансного интеграла
упрощает
количественные
расчеты
резонансного
поглощения без детального рассмотрения взаимодействия
нейтронов при замедлении.
Эффективный резонансный интеграл обычно определяют
экспериментально.
Он зависит от концентрации 238U и взаимного
расположения урана и замедлителя.

58.

ГОМОГЕННАЯ СИСТЕМА
• В гомогенной смеси замедлителя и 238U эффективный
резонансный интеграл с хорошей точностью находят
по эмпирической формуле
Jeff = 3,9 (Nз /N8 σs3) 0,415
• где N3/N8 — отношение ядер замедлителя и
гомогенной смеси;
238U
в
• σ3S — микроскопическое сечение рассеяния замедлителя.
• Как видно из формулы, эффективный резонансный интеграл
уменьшается с ростом концентрации 238U.
• Чем больше ядер 238U в смеси, тем менее вероятно
поглощение отдельным ядром замедляющихся нейтронов.

59.

ГОМОГЕННАЯ СИСТЕМА
• Чем больше ядер 238U в смеси, тем менее вероятно
поглощение отдельным ядром замедляющихся
нейтронов.
• Влияние поглощений в одних ядрах 238U на поглощение
в других называют экранировкой резонансных
уровней.
• Она растет с увеличением концентрации резонансных
поглотителей.
• Рассчитаем для примера эффективный резонансный
интеграл в гомогенной смеси природный уран—графит
с отношением N3/N8=215.
• Сечение рассеяния графита σCS = 4,7 барн:
Jeff = 3,9 (215 · 4,7 ) 0,415 = 69 барн.

60.

ГЕТЕРОГЕННАЯ СИСТЕМА
• В гомогенной среде все ядра 238U находятся в одинаковых
условиях по отношению к потоку резонансных нейтронов. В
гетерогенной среде уран отделён от замедлителя, что
существенно сказывается на резонансном поглощении
нейтронов.
– Во-первых, часть резонансных нейтронов становятся тепловыми
в замедлителе, не сталкиваясь с ядрами урана;
– во-вторых,
резонансные
нейтроны,
попадающие
на
поверхность ТВЭЛов, почти все поглощаются тонким
поверхностным слоем.
• Внутренние ядра 238U экранируются поверхностными и меньше
участвуют в резонансном поглощении нейтронов, причем
экранировка растет с увеличением диаметра ТВЭЛа d.
• Поэтому эффективный резонансный интеграл 238U в
гетерогенном реакторе зависит от диаметра ТВЭЛа d:

61.

ГЕТЕРОГЕННАЯ СИСТЕМА
Jeff = a + b/ √d,
• Постоянная a характеризует поглощение резонансных
нейтронов поверхностными, а
• постоянная b — внутренними ядрами 238U.
• Для каждого сорта ядерного топлива (природный уран,
двуокись урана и пр.) постоянные a и b измеряются
экспериментально.
• Для стержней из природного урана а=4,15, b=12,35.
Jeff = 4,15 +12,35 / √d,
• где Jeff — эффективный резонансный интеграл, барн;
d — диаметр стержня, см.

62.

ГЕТЕРОГЕННАЯ СИСТЕМА
• Найдём для примера эффективный резонансный
интеграл 238U для стержня из природного урана
диаметром d = 3 см:
Jeff = 4,15 +12,35 / √3 ≈ 11,3 барн.
• Сравнение двух последних примеров показывает, что
• при
разделении
урана
и
замедлителя
заметно
уменьшается поглощение нейтронов в резонансной
области.

63.

ВЛИЯНИЕ ЗАМЕДЛИТЕЛЯ
• Pассчитаем вероятность избежать резонансного захвата в
гомогенной и гетерогенной средах природный уран—графит.
• В обеих средах отношение ядер углерода и 238U NC/NS=215.
Диаметр уранового стержня d=3 см.
• Учитывая, что ξC=0,159, a σCa=4,7 барн, получаем
• N8 / (ξ σsC N c) = 1 /(0,159 4,7 215) = = 0,00625 барн-1
• Найдем коэффициенты гомогенной φгом и гетерогенной
ϕгет систем:
• ϕгом = e−0,00625·68 = e−0,425 ≈ 0,65,
• ϕ гет = e−0,00625·11,3 = e−0,0705 ≈0,93.

64.

ВЛИЯНИЕ ЗАМЕДЛИТЕЛЯ
• Переход от гомогенной среды к гетерогенной несколько
снижает поглощение тепловых нейтронов в уране.
• Однако этот проигрыш значительно перекрывается
уменьшением резонансного поглощения нейтронов, и
размножающие свойства среды улучшаются.
• Коэффициент ϕ зависит от отношения
N8 Jeff / ξ Σs = Σ / ξ Σs
• которое отражает конкуренцию двух процессов в
резонансной области:
• поглощение нейтронов и
• замедление нейтронов.

65.

ВЛИЯНИЕ ЗАМЕДЛИТЕЛЯ
• Сечение
Σ,
по
определению,
аналогично
макроскопическому сечению поглощения с заменой
микроскопического
сечения
эффективным
резонансным интегралом Jeff.
• Оно также характеризует убыль замедляющихся
нейтронов в резонансной области.
238U
• С
ростом
концентрации
поглощение
резонансных
нейтронов
увеличивается
и,
следовательно, меньше нейтронов замедляется до
тепловых энергий.

66.

ВЛИЯНИЕ ЗАМЕДЛИТЕЛЯ
• На резонансное поглощение оказывает
влияние замедление нейтронов.
• Столкновения с ядрами замедлителя выводят
нейтроны из резонансной области и тем
интенсивнее, чем больше замедляющая
способность ξ Σs .
• Значит, при одинаковой концентрации 238U
вероятность избежать резонансного захвата в
среде уран-вода больше, чем в среде урануглерод.

67.

НЕЙТРОННАЯ ОПТИКА
• раздел нейтронной физики, в котором изучаются
волновые свойства нейтрона, процессы распространения
нейтронных волн в разных веществах и полях. К числу
таких процессов относятся дифракция и интерференция
нейтронных
волн,
преломление
и
отражение
нейтронных пучков на границе раздела двух сред.
• В силу принципа корпускулярно-волнового дуализма
нейтрон может проявлять себя как частица с энергией Е и
импульсом p или как волна с частотой ω, длиной волны
λ= h /p и волновым вектором k = 2pр/ h.
• Волновые свойства отчётливо проявляются у нейтронов
низких энергий, длина волны которых порядка или
больше межатомных расстояний в веществе (~10-8 см).

68.

НЕЙТРОННАЯ ОПТИКА
• Из-за отсутствия у нейтронов электрического заряда они
глубоко проникают внутрь большинства материалов, что
позволяет рассматривать их как достаточно прозрачные
среды для распространения нейтронных волн.
• Большая часть нейтронно-оптических явлений имеет
аналогию с оптическими явлениями, несмотря на различную
природу полей нейтронного и светового излучений.
Световые волны описываются уравнениями Максвелла, а
нейтронная волна (нейтронная волновая функция)
подчиняется уравнению Шрёдингера.
• Распространение волн в среде, согласно принципу Гюйгенса,
связано с их рассеянием и последующей интерференцией
вторичных волн.

69.

НЕЙТРОННАЯ ОПТИКА
• В случае нейтронов рассеяние обусловлено гл. обр. их
короткодействующим сильным взаимодействием с
атомными ядрами, в случае световых волн дальнодействующим
электромагнитным
взаимодействием с электронами атомных оболочек.
• Наличие у нейтрона магнитного момента приводит к
взаимодействию с магнитными моментами атомов, на
чём основано т. н. магнитное рассеяние нейтронов, не
имеющее аналогии в оптике.

70.

НЕЙТРОННАЯ ОПТИКА
• Неупругое рассеяние нейтронов можно сопоставить
с комбинационным рассеянием света. В отличие от
векторной световой волны, нейтронная волна является
спинором.
• Поэтому все поляризационные явления в нейтронной
оптике, связанные с наличием у нейтрона спина,
существенно отличаются от оптических, хотя и здесь есть
аналогии; напр., поляризации нейтронов можно (в
некотором
приближении)
сопоставить
круговую поляризацию света.
• В нейтронной оптике в некоторых случаях имеет
место двойное лучепреломление и дихроизм
• Дихрои́зм — явление, состоящее в различном поглощении
веществом света в зависимости от его поляризации..

71.

Поляризованные нейтроны
• - совокупность нейтронов, спины которых имеют
преимущественную ориентацию по отношению к какомулибо выделенному направлению в пространстве, обычно
направлению магнитного поля.
• Т. к. нейтрон обладает спином 1/2, то в магнитном
поле Н возможны 2 ориентации его спина:
– параллельно или
– антипараллельно Н.
• Нейтронный пучок поляризован, если он содержит разное
количество N нейтронов со спинами, ориентированными
вдоль (N+) и против поля (N-).
• Степень поляризации характеризуют величиной
P = (N+ — N-)/(N+ + N-).

72.

Вопросы
• Дифракция - огибание волнами препятствий, в современном,
более широком - любые отклонения при распространении волн
от законов геометрической оптики.
• К дифракции фактически относят все эффекты, возникающие
при взаимодействии волн с объектом любых размеров, даже
малых по сравнению с длиной падающей волны, когда
сопоставление с лучевым приближением совершенно не
показательно.
• При таком общем толковании дифракции тесно переплетается
с явлениями распространения и рассеяния волн в
неоднородных средах.
• Интерференция - взаимное увеличение или уменьшение
результирующей
амплитуды
двух
или
нескольких
когерентных волн при их наложении друг на друга.
Сопровождается чередованием максимумов и минимумов
интенсивности в пространстве.

73.

Вопросы
• Спинор
- специальное обобщение понятия
вектора, применяемое для лучшего описания
группы
вращений
евклидова
или
псевдоевклидова пространства.
• Принцип Гюйгенса: Каждый элемент волнового
фронта можно рассматривать как центр
вторичного
возмущения,
порождающего
вторичные сферические волны, а результирующее
световое поле в каждой точке пространства будет
определяться интерференцией этих волн.

74.

Распространение нейтронных волн в среде
• Для нейтронов с энергией Е, распространяющихся в свободном
пространстве,
решением
уравнения
Шрёдингера
(нерелятивистское приближение) является суперпозиция
плоских
{Akexp[i(wt - kr)]} и
сферических {(ai/r)exp[i(wt - -kri)]} волн,
где w = 2p Е /h - частота волны,
k = 2pmu/h - волновой вектор,
k = |k| - волновое число,
r - радиус-вектор точки,
ri - расстояние от i-гo точечного источника нейтронных
волн или рассеивателя.
• Конкретное решение зависит от граничных условий задачи и
выбирается
путём
определения
соответствующих
амплитуд Ak и ai плоских и сферических волн.

75.

Распространение нейтронных волн в среде
• Анализ задачи о распространении нейтронной волны в
среде показывает, что интерференция плоской первичной
волны, имеющей волновой вектор k, с рассеянными
сферическими волнами приводит к быстрому затуханию
первичной волны.
• Вместо неё в среде распространяется волна с волновым
вектором kcp, величина которого даётся соотношением:
где N - число ядер-рассеивателей в единице объёма,
b - т. н. когерентная длина рассеяния нейтрона на
закреплённом ядре.
• Длина рассеяния b связана с сечением упругого
когерентного
рассеяния
медленных
нейтронов
соотношением:

76.

Распространение нейтронных волн в среде
• Оно соответствует рассеянию на непроницаемой сфере
радиуса b. Для большинства ядер длина b > 0 и по порядку
величины равна размеру ядра (~10-12 см).
• Длины рассеяния являются эмпирическими величинами,
нерегулярно меняющимися от ядра к ядру.
• Для среды, содержащей различные атомные ядра,
произведение Nb в ф-ле (1) должно быть заменено на сумму
• Направление распространяющейся в среде волны определяется
из условия равенства параллельных границе раздела вакуум среда компонент волновых векторов k|| = k||cp, и ф-ла (1)
фактически связывает только нормальные компоненты
векторов k| и k|cp, т. е. (k|cp)2 = (k|)2 - 4pNb.
• Отсюда следует известный из оптики закон преломления
• sinq = nsinq', где q и q' - углы падения и преломления, а п показатель преломления среды для нейтронных волн:

77.

Распространение нейтронных волн в среде
Особые
дифракционные
явления
возникают
при
прохождении
нейтронов
через
кристаллы,
когда
интерференция нейтронных волн, рассеянных на регулярно
расположенных рассеивателях, приводит к усилению
интенсивности волн в направлениях, соответствующих
зеркальному отражению от атомных плоскостей кристалла
при выполнении Брэгга - Вульфа условия:
l l = 2 d cosq,
где l - кратность отражения,
d - межплоскостное расстояние,
q - угол падения нейтронов на отражающую атомную
плоскость.

78.

Распространение нейтронных волн в среде
• T. к. нейтрон обладает массой т, то изменение волнового
числа при преломлении на границе среды означает
изменение не только его импульса, но и кинетической
энергии.
• Следовательно, среде можно приписать некоторый
эффективный (оптический) потенциал U. Связь показателя
преломления n и U определяется выражением:
• Сравнивая (2) и (3), получаем:

79.

Распространение нейтронных волн в среде
• T. к. для большинства ядер b > 0, то взаимодействие
нейтронов со средой, как правило, носит характер
отталкивания (U > 0).
• Величина потенциала U мала для всех материалов
(<3.10-7 эВ).
• Для тепловых нейтронов с энергией 10-2 эВ мало
отличается от 1. При b > 0 n2 < 1 и уменьшается с
уменьшением Е.
• Крайне медленные нейтроны (ультрахолодные
нейтроны) с энергией Е < U не могут проникнуть внутрь
материала и полностью отражаются от его поверхности
аналогично отражению световых волн от поверхности
металлических зеркал.

80.

Распространение нейтронных волн в среде
• В
случае
магнитных
материалов
кроме
взаимодействия нейтрона с атомными ядрами следует
учитывать его взаимодействие с магн. моментами
электронных оболочек (магнитная нейтронография).
Для очень медленных нейтронов необходимо также
принимать во внимание и наличие силы тяжести .

81.

Распространение нейтронных волн в среде
• В результате к оптичесскому потенциалу добавляются
потенциалы
• UM = -mB, Urрав = mgz,
• где m - магн. момент нейтрона, В - магн. индукция,
• g - ускорение свободного падения, z - высота.
• Общее выражение для показателя преломления имеет
вид:

82.

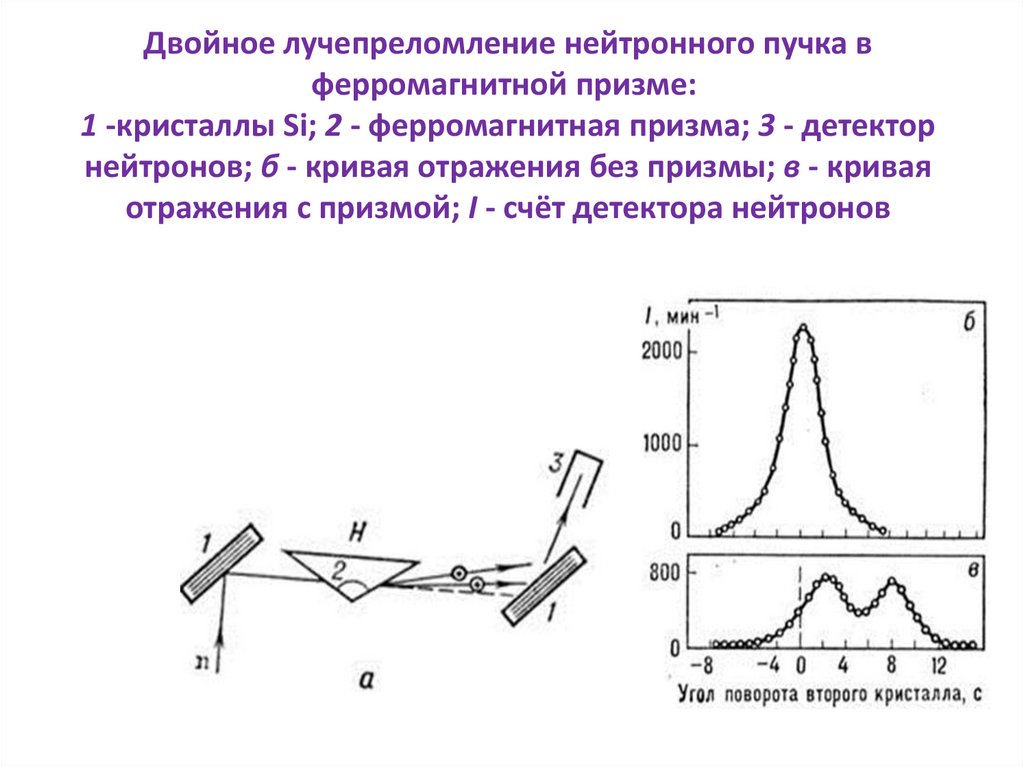
Двойное лучепреломление нейтронного пучка в
ферромагнитной призме:
1 -кристаллы Si; 2 - ферромагнитная призма; 3 - детектор
нейтронов; б - кривая отражения без призмы; в - кривая
отражения с призмой; I - счёт детектора нейтронов

83.

Распространение нейтронных волн в среде
• Неоднородность химического состава среды,
наличие гравитационного и магнитного членов в
(5) приводят к зависимости n от координат.
• При этом, как и в оптике неоднородных сред,
имеет место искривление лучей.
• Наличие двух знаков у последнего слагаемого в
(5) соответствует двум возможным ориентациям
спина нейтрона относительно H.

84.

Распространение нейтронных волн в среде
• Различие показателя преломления для двух
спиновых компонент приводит к магнитному
двойному лучепреломлению (рис.).
• Пучок нейтронов испытывает последовательно
брэгговскую дифракцию на двух кристаллах Si.
Расположенная между ними ферромагнитная
призма по-разному отклоняет нейтроны с
ориентацией спина параллельно полю ( ) и
антипараллельно ( ).

85.

Распространение нейтронных волн в среде
• В результате дифракционное отражение от 2-го
кристалла
Si
происходит
при
двух
разных
поворотах кристалла и регистрируются два пика,
соответствующие
двум
противоположным
ориентациям спина нейтрона.
• Из-за
спиновой
зависимости
ядерных
сил
двойное лучепреломление имеет место также в
среде,
содержащей
ориентированные
ядра (ядерный псевдомагнетизм).

86.

Распространение нейтронных волн в
среде
• Анализируя дифракционную картину, возникающую
при прохождении нейтронов через кристаллические
вещества, можно восстановить пространственную
структуру элементарной ячейки кристалла.
• В свою очередь, монокристаллы используются как
монохроматоры нейтронов.
• Явление полного отражения используется для
создания зеркальных нейтроноводов, с помощью
которых можно выводить нейтроны из ядерного
реактора или другого нейтронного источника на
достаточно большие расстояния.

87.

Распространение нейтронных волн в
среде
• T. к. показатель преломления определяется не только
ядерным составом среды, но и её магнитными
свойствами, то можно подобрать такие материалы,
для которых полное отражение имеет место только
для одной спиновой компоненты.
• На этом принципе основано действие поляризующих
зеркал и поляризующих нейтроноводов.

88.

НЕЙТРОНОГРАФИЯ
• совокупность методов исследования структуры и свойств
ве-щества с помощью рассеяния нейтронов низких
энергий ( <= 1 эВ).
• Длина волны де Бройля медленных нейтронов соизмери
ма смежатомными расстояниями в конденсированных
средах,
что позволяет изучать взаимное расположение атомов .
• Масса и кинетическая энергия нейтрона соизмерим
ы
с
массой
атома
и энергией
межатомных
взаимодействий в веществе, т.о. с помощью неупругого
рассеяния
нейтронов
можно
исследовать
динамические
свойства
отдельных
атомов и молекул в среде.

89.

НЕЙТРОНОГРАФИЯ
• Магнитный момент нейтрона взаимодействует с
магнитными моментами атомов, что позволяет
по интенсивности и поляризации магнитного
рассеяния определять величины магнитных
моментов атомов, их взаимное расположение,
ориентацию, динамические свойства вещества.

90.

НЕЙТРОНОГРАФИЯ
Hейтронография применяется для исследования структурных,
динамических и магнитных свойств практически всех
известных форм конденсированного состояния вещества:
– от простых жидкостей и кристаллов до
биологических макромолекул.
• Рассеяние нейтронов веществом принято классифицировать
• по следующим признакам:
– по изменению энергии нейтрона при рассеянии (упругое, неупругое);
– по характеру взаимодействия, ответственного за рассеяние(ядерное, м
агнитное);
– по степени когерентности нейтронных волн, рассеянных от множества
центров, образующих изучаемое вещество.