Основы метрологии. Терминология метрологии

1. Основы метрологии

2. Терминология метрологии

• В метрологии используются следующие
основные понятия и определения:
• физическая величина – одно из свойств
физического объекта (физической системы,
явления
или
процесса),
общее
в
качественном отношении для многих
физических объектов, но в количественном
отношении индивидуальное для каждого из
них;
Введение
2

3.

• измеряемая физическая величина
–
физическая
величина,
подлежащая
измерению, измеряемая или измеренная в
соответствии
с
основной
целью
измерительной задачи;
Введение
3

4.

• единица
измерения
физической
величины
– физическая величина
фиксированного размера, которой условно
присвоено числовое значение, равное 1,
применяемая
для
количественного
выражения однородных с ней физических
величин;
Введение
4

5.

• система единиц физических величин –
совокупность основных и произвольных
единиц физических величин, образованная
в соответствии с принципами для заданной
системы физических величин;
Введение
5

6.

• размер физической величины
–
количественная
определенность
физической
величины,
присущая
конкретному
материальному
объекту,
системе, явлению или процессу;
Введение
6

7.

• значение физической величины –
выражение размера физической величины в
виде некоторого числа принятых для нее
единиц (конкретное значение физической
величины является результатом ее измерения);
Введение
7

8.

• истинное
значение
физической
величины
–
значение
физической
величины, которое идеальным образом
характеризует
в
качественном
и
количественном
отношении
соответствующую физическую величину;
Введение
8

9.

• действительное значение физической
величины
–
значение
физической
величины, полученное экспериментальным
путем и настолько близкое к истинному
значению,
что
в
поставленной
измерительной
задаче
может
быть
использовано вместо него (например, при
поверке некоторого прибора его показания
сравнивают с показаниями более точного
(образцового)
прибора,
принимаемые
за
действительное значение величины);
Введение
9

10.

• измерение физической величины –
совокупность операций по применению
технического средства, хранящего единицу
физической величины, обеспечивающих
нахождение соотношения (в явном или
неявном виде) измеряемой величины с ее
единицей и получение значения этой
величины (установление значения физической
величины
опытным
путем
с
специальных технических средств);
Введение
помощью
10

11.

• результат
измерения
физической
величины
–
значение
величины,
полученное путем ее измерения –
установленное
значение
величины,
характеризующей свойство физического
объекта, представляемое действительным
числом с принятой размерностью;
• точность
измерений
–
одна
из
характеристик измерения, отражающая
близость к нулю погрешности результата
измерения;
Введение
11

12.

• средство измерений – техническое
средство, предназначенное для измерений,
имеющее нормированные метрологические
характеристики, воспроизводящее и (или)
хранящее единицу физической величины,
размер которой принимают неизменным (в
пределах установленной погрешности) в
течение известного интервала времени;
Введение
12

13.

• мера физической величины – средство
измерений,
предназначенное
для
воспроизведения
и
(или)
хранения
физической
величины
одного
или
нескольких заданных размеров, значения
которых выражены в установленных
единицах и известны с необходимой
точностью.
Введение
13

14.

• мера точности – погрешность результата
измерения – отклонение результата
измерения от истинного (действительного)
значения измеряемой величины (истинное
значение
величины
неизвестно,
его
применяют
только
в
теоретических
исследованиях, на практике используют
действительное значение);
Введение
14

15. Классификация погрешностей

• Любые
измерения
направлены
на
получение результата, то есть оценки
истинного значения физической величины
в принятых единицах измерения.
• Вследствие несовершенства средств и
методов измерений, воздействия внешних
факторов и многих других причин
результат каждого измерения неизбежно
отягощен погрешностью.
Введение
15

16.

• Качество измерения тем выше, чем ближе
результат
измерения
к
истинному
значению.
• Количественной характеристикой качества
измерений
является
погрешность
измерения.
Введение
16

17.

• Погрешность средства измерения – это
разность между показанием средства измерения
и истинным (действительным) значением
измеряемой величины. Поскольку истинное
значение физической величины неизвестно, то на
практике пользуются ее действительным
значением
Введение
17

18.

• Погрешность
результата
каждого
конкретного измерения складывается из
многих составляющих, обязанных своим
происхождением различным факторам и
источникам.
Введение
18

19.

• В
метрологии
принята
следующая
классификация погрешностей:
• По характеру проявления во времени:
систематическая погрешность измерения –
остающаяся постоянной или закономерно
изменяющаяся при повторных измерениях
одной и той же физической величины
(источником систематической погрешности
может
послужить,
например,
неточное
нанесение отметок на шкалу стрелочного
прибора, деформация стрелки);
Введение
19

20.

случайная погрешность – изменяющаяся
случайным образом (по знаку, значению)
при повторных измерениях одной и той же
физической величины, проведенных с
одинаковой тщательностью (возможна в
результате трения в опорах подвижной части
прибора, колебаний температуры окружающего
воздуха, влияния магнитных и электрических
помех и т.п.);
Введение
20

21.

промах
(грубая
погрешность)
–
погрешность
результата
отдельного
измерения, входящего в ряд измерений,
которая для данных условий резко
отличается от остальных результатов этого
ряда. Результат измерения с грубой
погрешностью должен быть отброшен,
как не вызывающий доверия.
Введение
21

22.

• По форме выражения:
абсолютная погрешность измерения Δ –
выраженная
в единицах
измерения.
определяется по формуле
Δ = Χп Χо,
Χо действительное значение измеряемой
величины;
Χп значение измеряемой физической
величины, найденное с помощью средства
измерений.
Введение
22

23.

относительная
погрешность
δ
–
отношение
абсолютной
погрешности
измерения
к
действительному
или
измеренному
значению
измеряемой
величины:
δ = Δ/Χо
δ = 100%*Δ/Χо, выраженная в процентах.
Точность может быть выражена обратной
величиной относительной погрешности –
1/δ.
Введение
23

24. Значащие цифры

• Стандарт СЭВ СТ СЭВ 543-77 «Числа.
Правила записи и округления»
• Значащие цифры – это все достоверно
известные цифры данного числа плюс
первая недостоверная цифра.
Введение
24

25.

• Достоверность результатов аналитических
определений
определяется
реальными
возможностями используемого метода или
методики.
• В качестве статистических критериев
оценки
недостоверности
результатов
анализа служит стандартное отклонение
или доверительный интервал.
Введение
25

26.

• Если вы лично проводили эксперимент, то
число значащих цифр вам наверняка
известно.
• В остальных случаях на помощь придут
следующие правила:
• 1) все ненулевые разряды являются
значащими;
• 2) нули не являются значащими в начале
числа, но являются – во всех остальных
случаях.

27.

• Так, числа 12,0; 0,0000120; 102 - все
содержат по 3 значащие цифры.
• Если же число корректно записано в
стандартном виде, то все его разряды перед
10^n являются значащими.
Введение
27

28.

• При записи результата анализа нули,
стоящие в конце числа следует исключить,
если они не являются значащими, а
результат представить в виде числа с
нормальной формой представления:
• a∙10^n, где 1 < a < 10.
Введение
28

29.

• Примеры.
• 1. Если число 1000 содержит 3 значащие
цифры, то правильная запись - 1,00∙10^3.
• Если в нем 4 значащие цифры, то число
следует записать как 1,000∙10^3.
• 2. Масса образца равна 0,1 г. Если
взвешивание проводили на аналитических
весах с погрешностью ±0,0002 г, то
правильное представление результата –
0,1000 г или 1,000∙10-1 г.
Введение
29

30.

• Когда необходимо указать, что число
является точным, после числа должно быть
указано слово "точно" или же последняя
значащая цифра печатается жирным
шрифтом.
• Пример.
• 1 кВт*ч = 3 600 000 Дж (точно), или =
3600000 Дж
• 1 кал = 1,484 Дж (точно), 1,484 Дж
Введение
30

31.

• Следует различать записи приближенных
чисел по количеству значащих цифр.
• Примеры:
• 1. Следует различать числа 2,4 и 2,40.
Запись 2,4 означает, что верны только
цифры целых и десятых; истинное значение
числа может быть например 2,43 и 2,38.
Запись 2,40 означает, что верны и сотые
доли числа; истинное число может быть
2,403 и 2,398, но не 2,421 и не 2,382.
Введение
31

32.

• 2. Запись 382 означает, что все цифры
верны; если за последнюю цифру ручаться
нельзя, то число должно быть записано
3.8*10^2 .
• 3. Если в числе 4720 верны лишь две
первые цифры, оно должно быть записано
или 4.7*10^3 .
Введение
32

33.

• Число,
для
которого
указывается
допускаемое отклонение, должно иметь
последнюю значащую цифру того же
разряда как и последняя значащая цифра
отклонения.
Введение
33

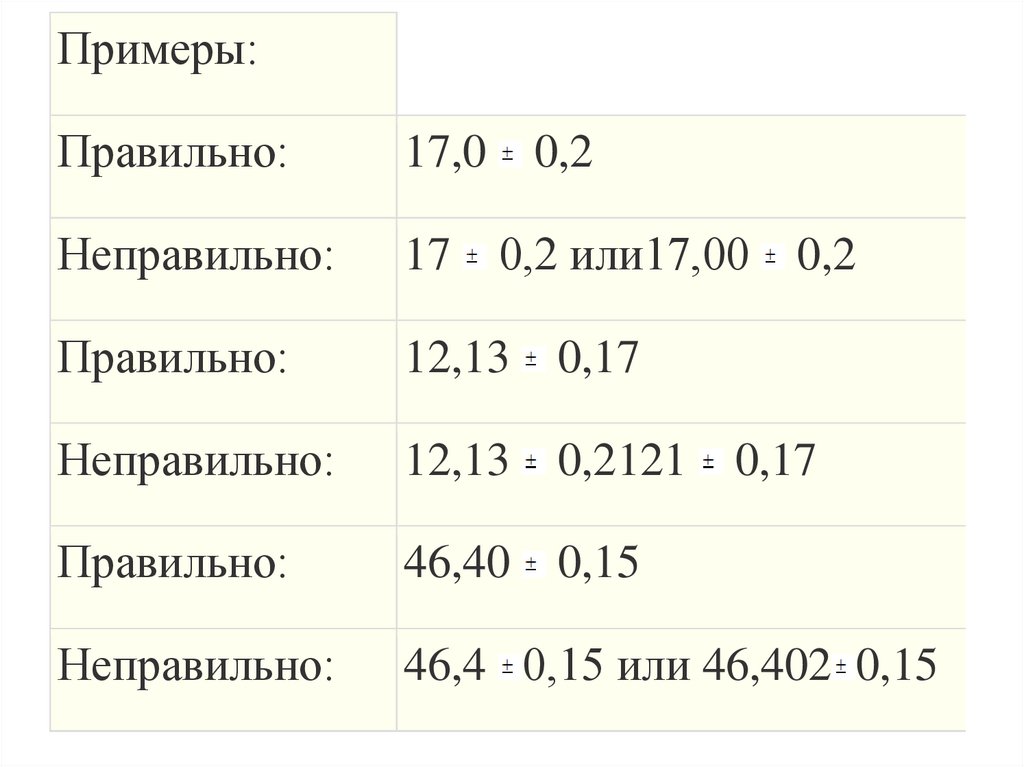
34.

Примеры:
Правильно:
17,0
Неправильно:
17
Правильно:
12,13
0,17
Неправильно:
12,13
0,2121
Правильно:
46,40
0,15
Неправильно:
46,4 0,15 или 46,402 0,15
0,2
0,2 или17,00
Введение
0,2
0,17
34

35. Правила округления:

• Незначащие цифры исключают, округляя
число.
• Если отбрасываемая цифра меньше 5, то
последняя значащая цифра не изменяется.
• Если отбрасываемая цифра больше или
равна 5, то последняя значащая цифра
увеличивается на единицу.
• Если за первой недостоверной цифрой следует
цифра 5, то применяют и другое правило:
округляют цифру 5 до ближайшего четного
числа.
Введение
35

36.

• В тех случаях, когда следует учитывать
результаты
предыдущих
округлений,
поступают следующим образом:
• 1) если отбрасываемая цифра получилась в
результате предыдущего округления в
большую
сторону,
то
последняя
сохраняемая цифра сохраняется;
• Пример. Округление до одной значащей
цифры числа 0,15 (полученного после
округления числа 0,149) дает 0,1.
Введение
36

37.

• В тех случаях, когда следует учитывать
результаты
предыдущих
округлений,
поступают следующим образом:
• 1) если отбрасываемая цифра получилась в
результате предыдущего округления в
большую
сторону,
то
последняя
сохраняемая цифра сохраняется;
• Пример. Округление до одной значащей
цифры числа 0,15 (полученного после
округления числа 0,149) дает 0,1.
Введение
37

38.

• 2) если отбрасываемая цифра получилась в
результате предыдущего округления в
меньшую
сторону,
то
последняя
оставшаяся цифра увеличивается на
единицу (с переходом при необходимости в
следующие разряды).
• Пример.
Округление
числа
0,25
(полученного в результате предыдущего
округления числа 0,252) дает 0,3.
Введение
38

39.

• Округление следует выполнять сразу до
желаемого количества значащих цифр, а не
по этапам.
• Пример. Округление числа 565,46 до трех
значащих
цифр
производится
непосредственно на 565.
• Округление по этапам привело бы к:
• 565,46 в I этапе-к 565,5,
• а во II этапе - 566 (ошибочно).
Введение
39

40.

• Целые числа округляют по тем же
правилам, что и дробные.
• Пример. Округление числа 12 456 до двух
значащих цифр дает 12*10^3
Введение
40

41.

• Естественно,
что
выполнение
вычислительных
операций
над
результатами измерений не может изменить
их неопределенности.
• Значит, после проведения вычислений
(например, с помощью калькулятора) их
результат должен быть соответствующим
образом округлен.
Введение
41

42.

• А. При умножении или делении число
значащих цифр в корректном ответе
должно равняться минимальному их
количеству в исходных данных.
• 8,03 (3 значащие цифры) • 4,9 (2 значащие
цифры) = = [39,347 (на дисплее
калькулятора)] = 39 (2 значащие цифры,
корректный ответ).
Введение
42

43.

• Б. При сложении или вычитании в
корректном ответе число разрядов справа
от десятичной запятой должно равняться
минимальному из таковых в исходных
данных.
• 9,348 (3 разряда после запятой) + 1,9 (1
разряд после запятой) = [11,248 (на дисплее
калькулятора)] = 11,2 (1 разряд после
запятой, корректный ответ).
Введение
43

44.

• В. При логарифмировании числа вида
А*10^n число разрядов после запятой в
логарифме должно совпадать с числом
значащих цифр в мантиссе (А), поскольку
перед запятой выходит порядок степени.
Пример: lg(6,02* 10^23) = 23,780.
Введение
44

45.

• Если ответ в задаче получается не в
результате единичного вычисления, а
многостадийным
расчетом,
то,
во
избежание накопления ошибок округления,
на промежуточных этапах рекомендуется
использовать на один разряд больше,
нежели число значащих цифр.
• В конечном результате эта цифра
округляется.
Введение
45