Похожие презентации:
Компьютерные технологии и математическое моделирование биологических процессов
1.
Экзаменационная работапо дисциплине
«Компьютерные технологии и математическое
моделирование биологических процессов»
Выполнила: студентка 1 курса гр. 131164
06.04.01. Биология (Прикладная психофизиология)
Титова Надежда Владимировна
Проверила: к.п.н., доцент каф. фундаментальной и прикладной физики
Ужовская Екатерина Михайловна
.
2.
Задачи:1. Проверить данные на нормальность распределения;
2. Провести корреляционный анализ;
3. Сформулировать выводы
3.
Описание базы данных• База данных состоит из баллов, полученных в результате психологического
тестирования самооценки и учебной мотивации студентов (50 человек);
• Выборка данных «Самооценка» была разделена на три подгруппы – низкая,
средняя и высокая самооценка соответственно интерпретации.
Для получения трех подгрупп данные были преобразованы следующим
образом:
1 – от 19 до 22 баллов (низкая самооценка); 2 – от 23 до 34 (средняя
самооценка); 3 – от 35 до 40 (высокая самооценка);
• Учебная мотивация состоит из трех выборок – приобретение знаний,
овладение профессией и получение диплома, соответственно шкалам
методики.
4.
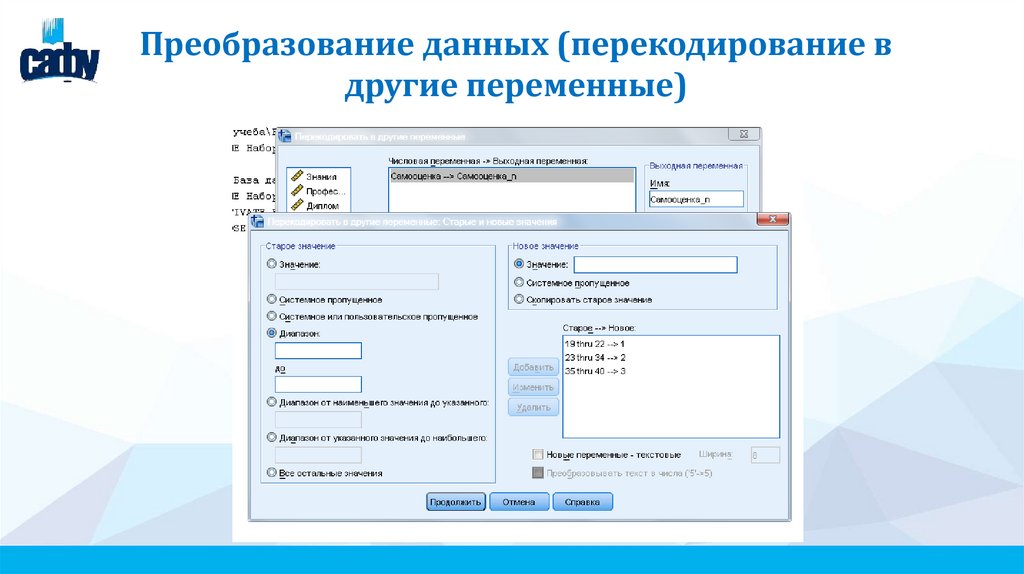
Преобразование данных (перекодирование вдругие переменные)
5.
Нулевые гипотезы:1. H0 – у людей с высокой и у людей со средней самооценкой
мотивация к овладению профессией не различается;
2. H0 – у людей с высокой и у людей со средней самооценкой
мотивация по получению диплома не различается;
2. H0 – у людей с высокой и у людей со средней самооценкой
мотивация к приобретению знаний не различается
Т.к. в данном исследовании было выявлено всего 5 человек с
низкой самооценкой, то они исключены из дальнейшей
статистической обработки, потому что полученные данные не
были бы статистически значимыми
6.
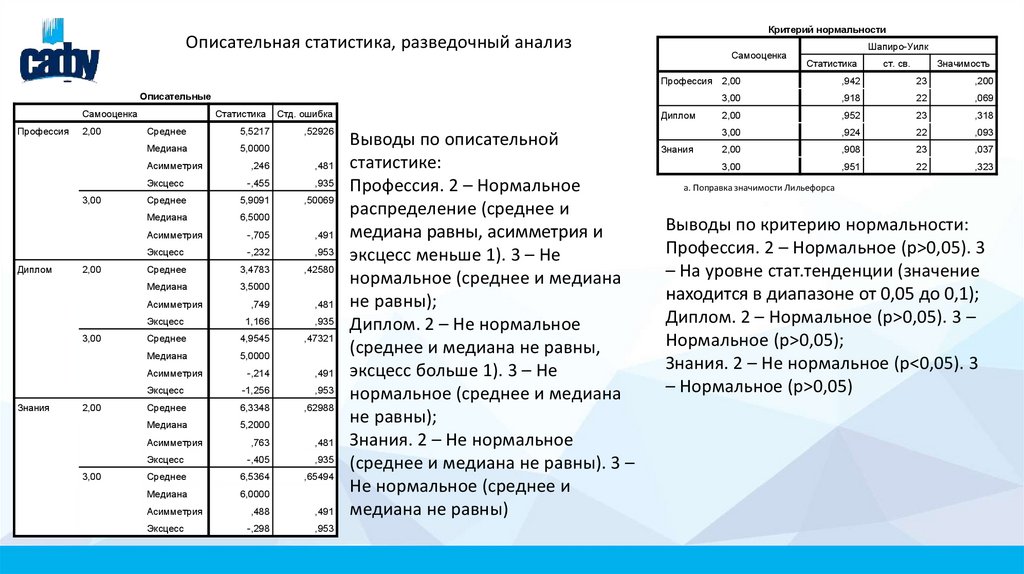
Критерий нормальностиОписательная статистика, разведочный анализ
Самооценка
Профессия
2,00
3,00
Диплом
2,00
3,00
Знания
2,00
3,00
Статистика
Стд. ошибка
Среднее
5,5217
,52926
Медиана
5,0000
Асимметрия
,246
,481
Эксцесс
-,455
,935
Среднее
5,9091
,50069
Медиана
6,5000
Асимметрия
-,705
,491
Эксцесс
-,232
,953
Среднее
3,4783
,42580
Медиана
3,5000
Асимметрия
,749
,481
Эксцесс
1,166
,935
Среднее
4,9545
,47321
Медиана
5,0000
Асимметрия
-,214
,491
Эксцесс
-1,256
,953
Среднее
6,3348
,62988
Медиана
5,2000
Асимметрия
,763
,481
Эксцесс
-,405
,935
Среднее
6,5364
,65494
Медиана
6,0000
Асимметрия
,488
,491
Эксцесс
-,298
,953
ст. св.
Значимость
,942
23
,200
3,00
,918
22
,069
2,00
,952
23
,318
3,00
,924
22
,093
2,00
,908
23
,037
3,00
,951
22
,323
Диплом
Выводы по описательной
статистике:
Профессия. 2 – Нормальное
распределение (среднее и
медиана равны, асимметрия и
эксцесс меньше 1). 3 – Не
нормальное (среднее и медиана
не равны);
Диплом. 2 – Не нормальное
(среднее и медиана не равны,
эксцесс больше 1). 3 – Не
нормальное (среднее и медиана
не равны);
Знания. 2 – Не нормальное
(среднее и медиана не равны). 3 –
Не нормальное (среднее и
медиана не равны)
Статистика
Профессия 2,00
Описательные
Самооценка
Шапиро-Уилк
Знания
a. Поправка значимости Лильефорса
Выводы по критерию нормальности:
Профессия. 2 – Нормальное (p>0,05). 3
– На уровне стат.тенденции (значение
находится в диапазоне от 0,05 до 0,1);
Диплом. 2 – Нормальное (p>0,05). 3 –
Нормальное (p>0,05);
Знания. 2 – Не нормальное (p<0,05). 3
– Нормальное (p>0,05)
7.
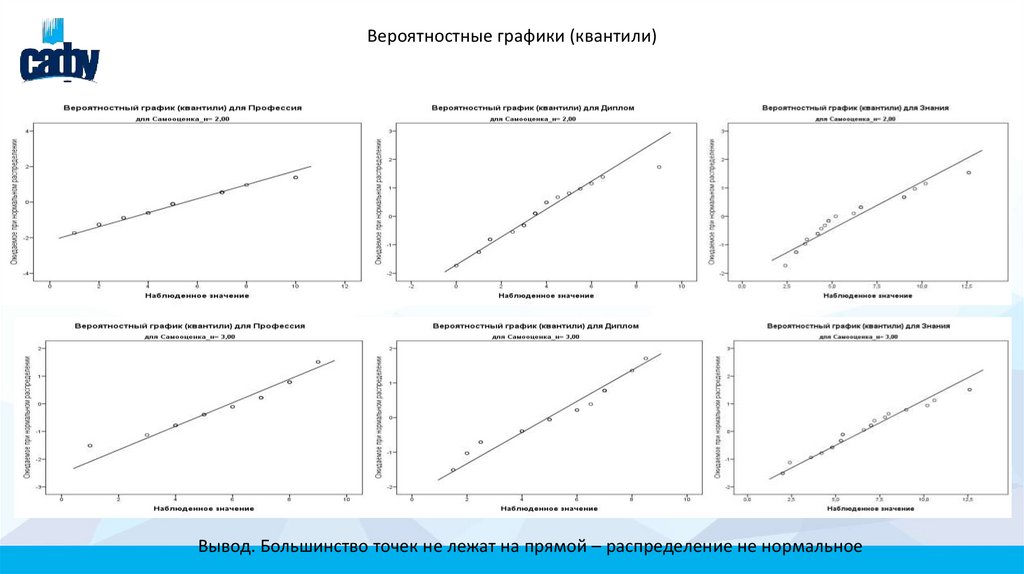
Вероятностные графики (квантили)Вывод. Большинство точек не лежат на прямой – распределение не нормальное
8.
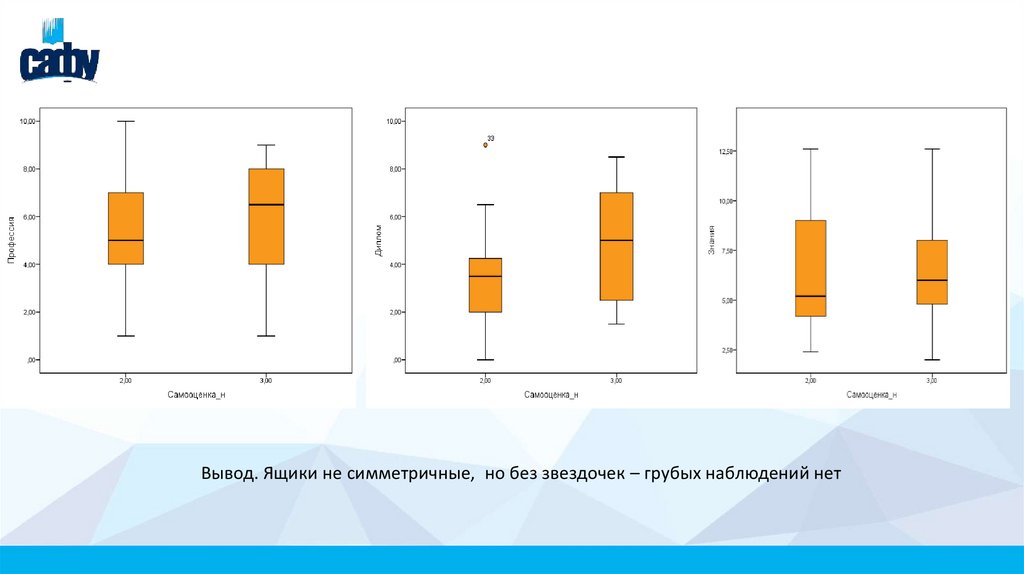
Вывод. Ящики не симметричные, но без звездочек – грубых наблюдений нет9.
Выводы о нормальности распределения• В целом, по описательной статистике, распределение не нормальное,
по критерию Шапиро-Уилка в большинстве нормальное, но также есть
значение на уровне стат.тенденции;
• На вероятностном графике большинство точек не лежат на прямой –
распределение не нормальное, ящики не симметричные, но без
звездочек – грубых наблюдений нет.
Таким образом, распределение не нормальное, без грубых
наблюдений, и так как имеется две не связанные выборки, то для
корреляционного анализа выбираем непараметрический U-критерий
Манна-Уитни.
10.
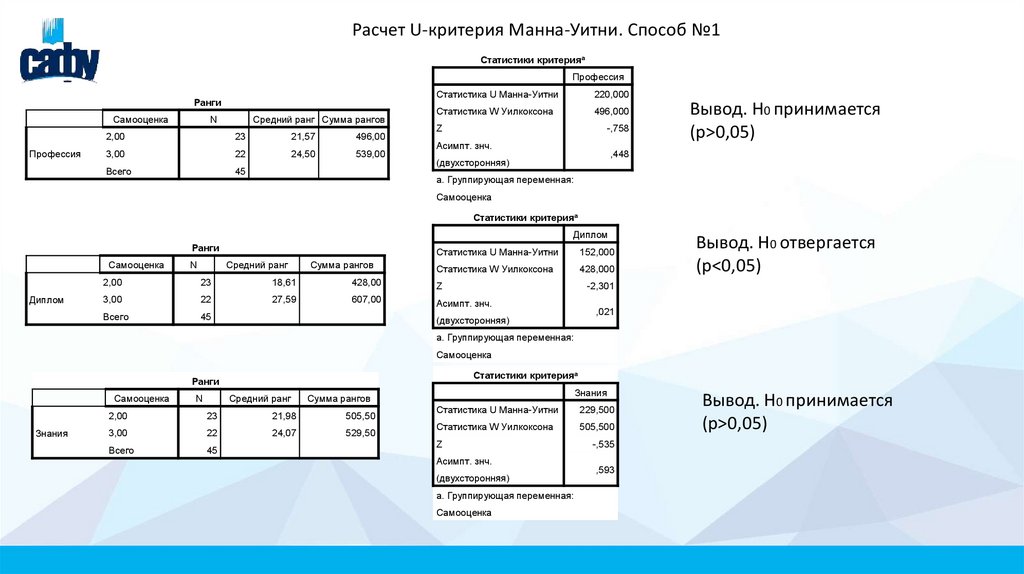
Расчет U-критерия Манна-Уитни. Способ №1Статистики критерияa
Профессия
Ранги
Самооценка
Профессия
Средний ранг Сумма рангов
N
2,00
23
21,57
496,00
3,00
22
24,50
539,00
Всего
45
Статистика U Манна-Уитни
220,000
Статистика W Уилкоксона
496,000
Z
-,758
Асимпт. знч.
Вывод. Н0 принимается
(p>0,05)
,448
(двухсторонняя)
a. Группирующая переменная:
Самооценка
Статистики критерияa
Диплом
Ранги
Самооценка
Диплом
Средний ранг
N
Сумма рангов
Статистика U Манна-Уитни
152,000
Статистика W Уилкоксона
428,000
2,00
23
18,61
428,00
Z
3,00
22
27,59
607,00
Асимпт. знч.
Всего
45
Вывод. Н0 отвергается
(p<0,05)
-2,301
,021
(двухсторонняя)
a. Группирующая переменная:
Самооценка
Статистики критерияa
Ранги
Самооценка
Знания
N
Средний ранг
Сумма рангов
2,00
23
21,98
505,50
3,00
22
24,07
529,50
Всего
45
Знания
Статистика U Манна-Уитни
229,500
Статистика W Уилкоксона
505,500
Z
Асимпт. знч.
(двухсторонняя)
a. Группирующая переменная:
Самооценка
-,535
,593
Вывод. Н0 принимается
(p>0,05)
11.
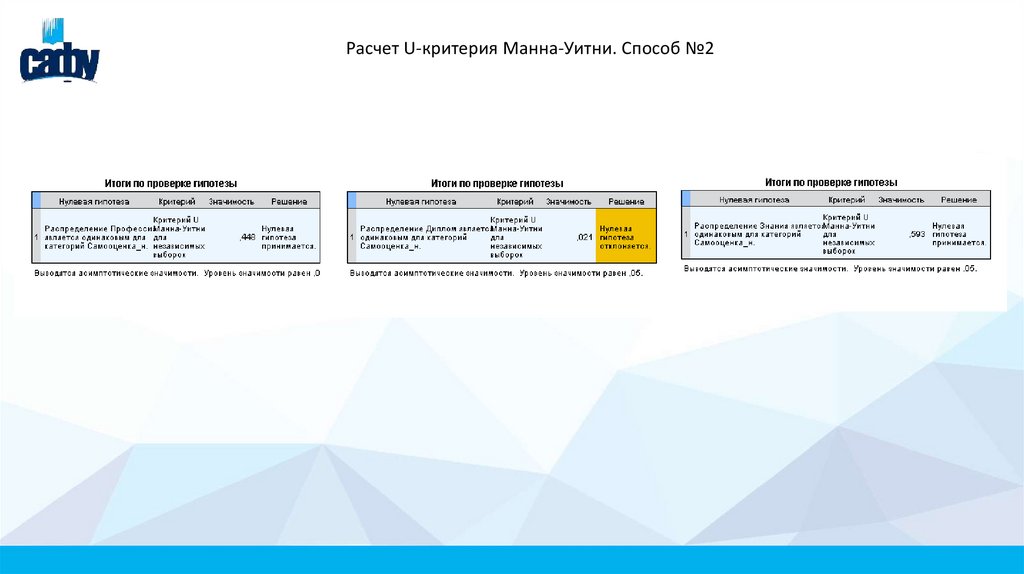
Расчет U-критерия Манна-Уитни. Способ №212.
Выводы по U-критерию Манна-Уитни1. Принимается (p>0,05) H0 – у людей с высокой и у людей со средней
самооценкой мотивация к овладению профессией не различается;
2. Отвергается (p<0,05) H0 – у людей с высокой и у людей со средней
самооценкой мотивация по получению диплома не различается;
3. Принимается (p>0,05) H0 – у людей с высокой и у людей со средней
самооценкой мотивация к приобретению знаний не различается
Таким образом, мотивация к овладению профессией и приобретению
знаний у людей с высокой и средней самооценкой не различается, а
мотивация по получению диплома - различается
13.
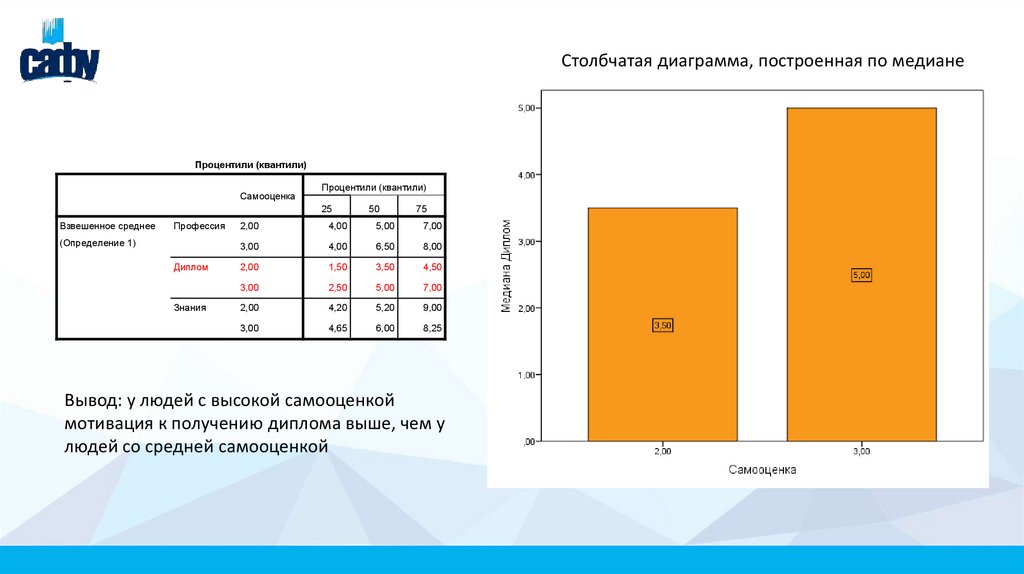
Столбчатая диаграмма, построенная по медианеПроцентили (квантили)
Самооценка
Процентили (квантили)
25
Взвешенное среднее
Профессия
(Определение 1)
Диплом
Знания
50
75
2,00
4,00
5,00
7,00
3,00
4,00
6,50
8,00
2,00
1,50
3,50
4,50
3,00
2,50
5,00
7,00
2,00
4,20
5,20
9,00
3,00
4,65
6,00
8,25
Вывод: у людей с высокой самооценкой
мотивация к получению диплома выше, чем у
людей со средней самооценкой







 Биология
Биология








