Похожие презентации:
Порядковое дерево. Дерево промежутков
1.
Порядковое деревоВ сбалансированном дереве поиска можно быстро найти заданный ключ, скорость та же, что и
в упорядоченном массиве. Однако элемент по его номеру быстро найти не удается. Точно так же,
если уже имеется ссылка на узел дерева, невозможно быстро определить его порядковый номер.
Упражнение: напишите функцию, которая ищет в дереве поиска элемент по его порядковому
номеру. Как можно оценить скорость работы алгоритма?
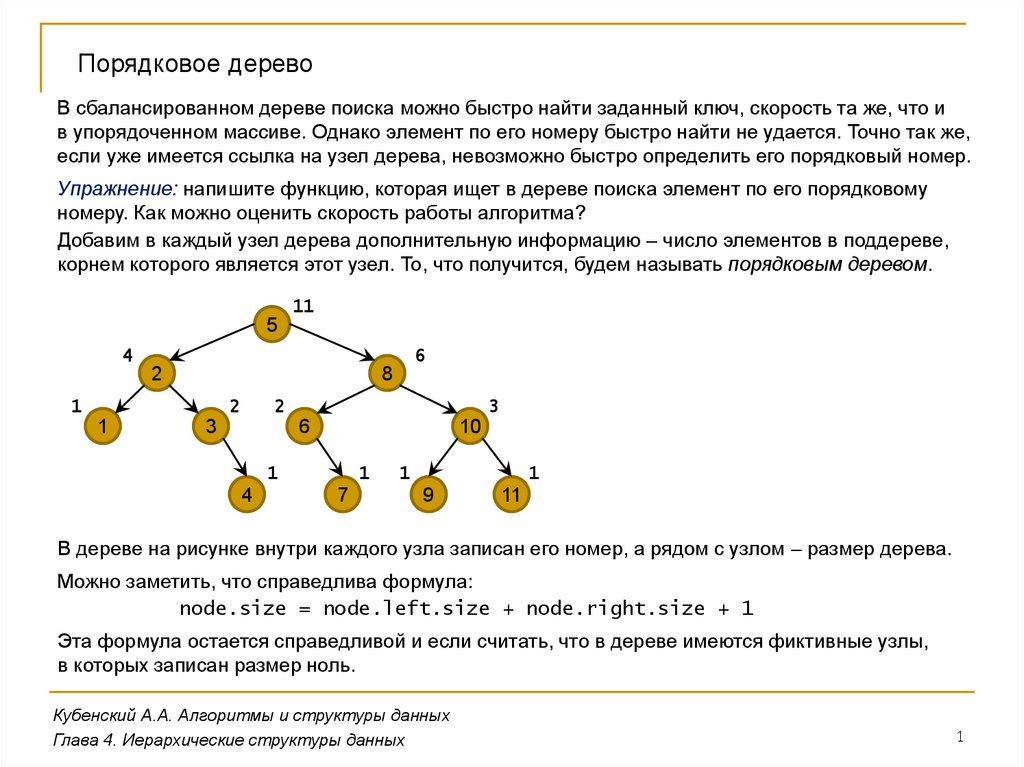
Добавим в каждый узел дерева дополнительную информацию – число элементов в поддереве,
корнем которого является этот узел. То, что получится, будем называть порядковым деревом.
11
5
4
6
2
8
1
2
1
2
3
3
6
10
1
4
1
7
1
1
9
11
В дереве на рисунке внутри каждого узла записан его номер, а рядом с узлом – размер дерева.
Можно заметить, что справедлива формула:
node.size = node.left.size + node.right.size + 1
Эта формула остается справедливой и если считать, что в дереве имеются фиктивные узлы,
в которых записан размер ноль.
Кубенский А.А. Алгоритмы и структуры данных
Глава 4. Иерархические структуры данных
1
2.
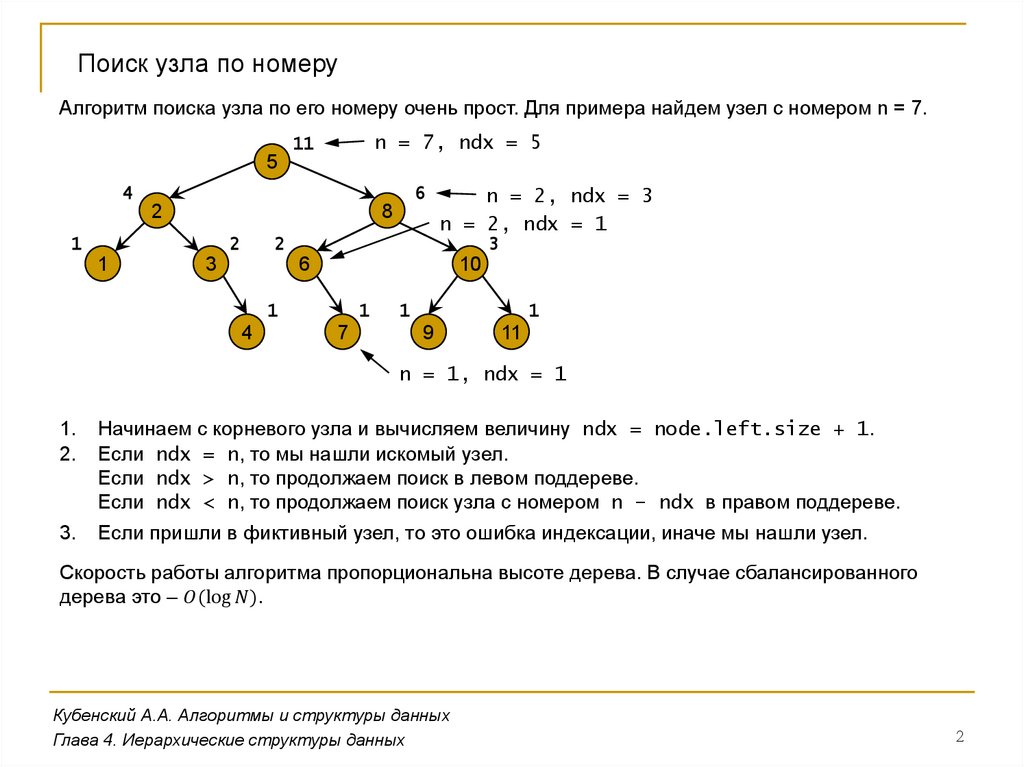
Поиск узла по номеруАлгоритм поиска узла по его номеру очень прост. Для примера найдем узел с номером n = 7.
n = 7, ndx = 5
11
5
4
6
2
8
1
2
1
n = 2, ndx = 3
n = 2, ndx = 1
2
3
3
6
10
1
4
1
7
1
1
9
11
n = 1, ndx = 1
1.
2.
Начинаем с корневого узла и вычисляем величину ndx = node.left.size + 1.
Если ndx = n, то мы нашли искомый узел.
Если ndx > n, то продолжаем поиск в левом поддереве.
Если ndx < n, то продолжаем поиск узла с номером n – ndx в правом поддереве.
3.
Если пришли в фиктивный узел, то это ошибка индексации, иначе мы нашли узел.
Скорость работы алгоритма пропорциональна высоте дерева. В случае сбалансированного
дерева это –







 Программирование
Программирование








