Перпендикуляр и наклонная (10 класс)

1.

Университетский лицей №1523
Предуниверситария НИЯУ МИФИ
Лекции по геометрии
10 класс
© Хомутова Лариса Юрьевна
© Крайко Мария Александровна

2.

Перпендикуляр и наклонная.

3.

1. Перпендикуляр и наклонная
Для построения параллельной проекции точки на плоскость необходимо
задать направление проектирования. Если направление проектирования
перпендикулярно плоскости проектирования, проектирование называется
ортогональным.
Например, точка M является ортогональной
проекцией точки M на плоскость ,
если MM , и M .
Отрезок MM называется при этом перпендикуляром, опущенным из точки M
на плоскость . Точка M - основание перпендикуляра.
Ортогональная проекция точки M или фигуры Ф на плоскость обозначается
следующим образом: M = M ; Ф = Ф .

4.

Если точка принадлежит плоскости проектирования, то она совпадает со
своей проекцией.
Для построения проекции прямой l на плоскость необходимо выбрать
любую точку B l, построить ее проекцию B = B , и провести прямую l
через B и точку A пересечения прямой l с плоскостью ; тогда l = l .
Если l , то для построения проекции прямой l на плоскость необходимо
построить проекции двух ее произвольных точек на эту плоскость и провести
через них прямую.

5.

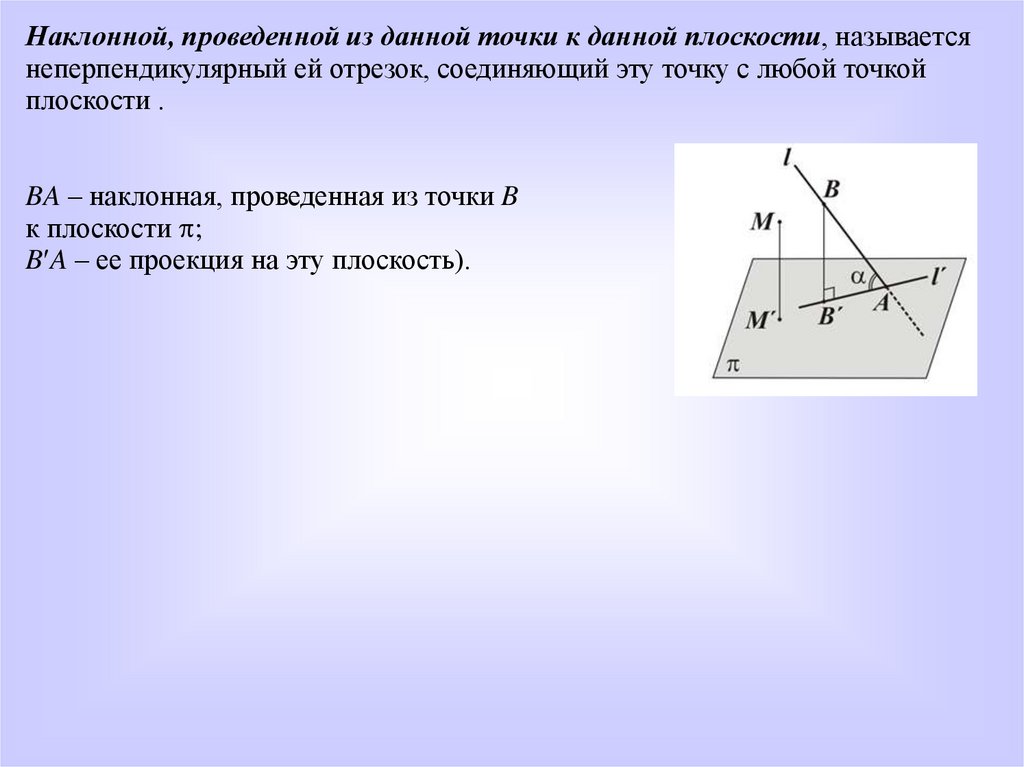
Наклонной, проведенной из данной точки к данной плоскости, называется
неперпендикулярный ей отрезок, соединяющий эту точку с любой точкой
плоскости .
BA – наклонная, проведенная из точки B
к плоскости ;
B A – ее проекция на эту плоскость).

6.

Наклонные, проведенные из точки к плоскости, обладают следующими
свойствами наклонных:
1) Наклонная, проведенная из точки к плоскости, всегда длиннее своей
проекции на эту плоскость .
AB < AB, т.к. катет в прямоугольном треугольнике AB B короче гипотенузы.
2) Наклонная, проведенная из точки к плоскости, всегда длиннее
перпендикуляра, опущенного из этой же точки на эту же плоскость.
BA > BB , как гипотенуза и катет прямоугольного треугольника AB B.
3) Если из одной точки к плоскости проведены две
наклонные, то их длины равны тогда и только тогда,
когда равны их проекции . AB = AC A B = A C;
4) Если из одной точки к плоскости
проведены две наклонные, то большей
наклонной соответствует большая
проекция, а большей проекции –
большая наклонная .
AB > AC A B > A C;

7.

2. Расстояния между простейшими фигурами
Расстоянием между фигурами называется расстояние между ближайшими точками
этих фигур.
Расстояние от точки до плоскости равно длине перпендикуляра, опущенного из
этой точки на плоскость; если же точка принадлежит плоскости, то расстояние от нее
до плоскости равно 0 (на рисунке (A; ) = AA ; (B; ) = 0).

8.

Ключевую задачу, позволяющая в ряде случаев находить расстояние от
точки до плоскости: Если прямая AB пересекает плоскость в точке O, то
.
AO A;
BO B;
1) Рассмотрим сначала случай, когда
AB . В этом случае AO = (A; ),
BO = (B; ), и равенство выполняется
автоматически
2) В случае, когда прямая AB – наклонная к плоскости , для нахождения расстояний от
точек A и B до плоскости необходимо опустить из них перпендикуляры AA и BB на
плоскость . При этом т.к. AA BB , AA BB по признаку параллельности
прямых, перпендикулярных плоскости. Значит, прямые AA и BB лежат в одной
плоскости AA B, причем O AB (AA B). А т.к. плоскости AA B и пересекаются по
прямой A B , O A B .
3) Осталось воспользоваться подобием прямоугольных треугольников AOA и BOB : они
подобны по двум углам, т.к. AOA = BOB либо как общий угол либо как вертикальные
углы . Из подобия треугольников вытекает пропорция AO AA A;
BO
BB
B;

9.

Расстояния между прямой и плоскостью.
Если прямая пересекает плоскость, расстояние между ними равно нулю.
Если прямая a параллельна плоскости ,
то расстояние от прямой до параллельной ей плоскости равно
расстоянию от любой точки этой прямой до плоскости.

10.

Расстояние между двумя плоскостями.
Если две плоскости пересекаются, то расстояние между ними равно нулю.
Если же плоскости и параллельны,
то
расстояние
между
двумя
параллельными
плоскостями
расстоянию от любой точки одной плоскости до второй плоскости.
равно

11.

Расстояние между двумя скрещивающимися прямыми
Через одну из скрещивающихся прямых проведем плоскость параллельную второй
прямой.
Тогда расстояние между двумя скрещивающимися прямыми равно расстоянию от
любой точки одной прямой до плоскости, проходящей через вторую прямую.

12.

3. Высота призмы и пирамиды
Высотой призмы называется перпендикуляр,
опущенный из любой точки одного ее основания к
плоскости второго основания
(на рисунке B1B1 , BnBn , XX - высоты призмы).
Замечание 1: Длины всех высот призмы равны
расстоянию между плоскостями ее оснований.
Замечание 2: Все боковые ребра прямой призмы
являются ее высотами.

13.

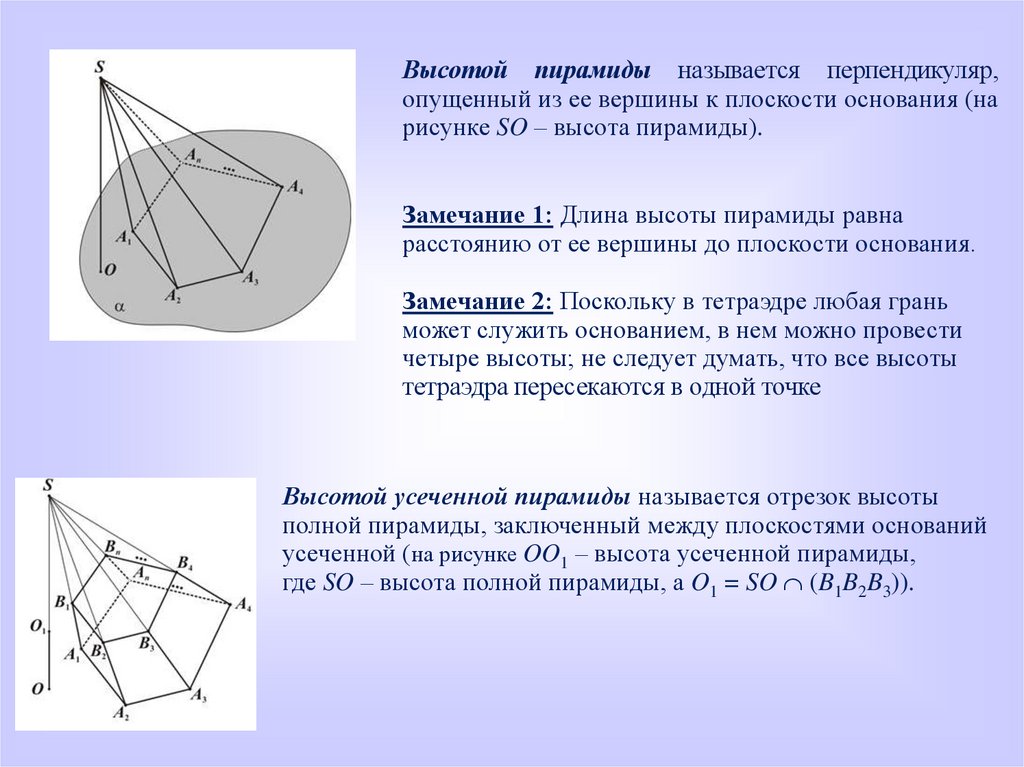
Высотой пирамиды называется перпендикуляр,
опущенный из ее вершины к плоскости основания (на
рисунке SO – высота пирамиды).
Замечание 1: Длина высоты пирамиды равна
расстоянию от ее вершины до плоскости основания.
Замечание 2: Поскольку в тетраэдре любая грань
может служить основанием, в нем можно провести
четыре высоты; не следует думать, что все высоты
тетраэдра пересекаются в одной точке
Высотой усеченной пирамиды называется отрезок высоты
полной пирамиды, заключенный между плоскостями оснований
усеченной (на рисунке OO1 – высота усеченной пирамиды,
где SO – высота полной пирамиды, а O1 = SO (B1B2B3)).