Похожие презентации:
Основные понятия теории множеств (лекция 1)
1.
Название дисциплины, МДК2.
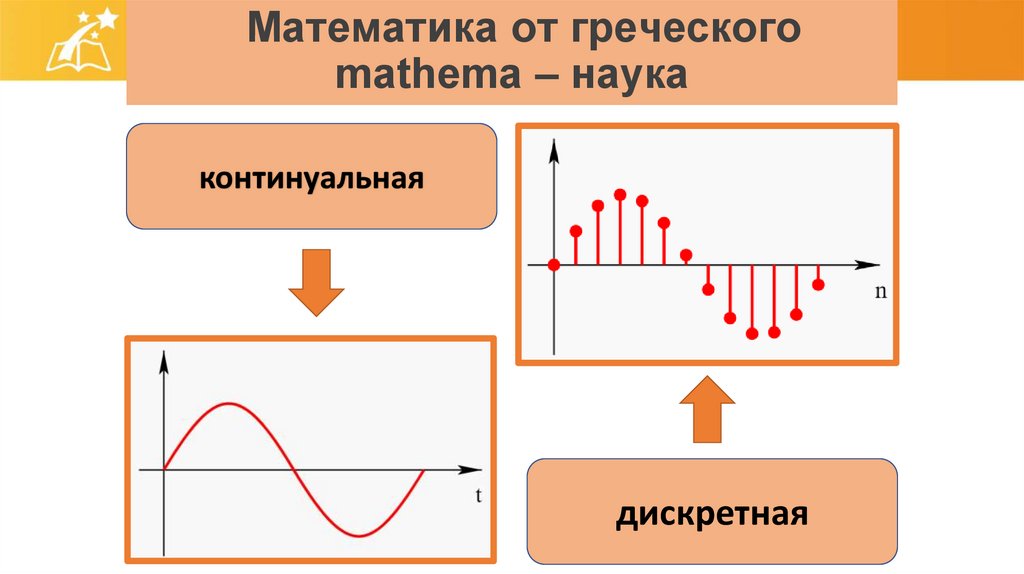
Математика от греческогоmathema – наука
континуальная
дискретная
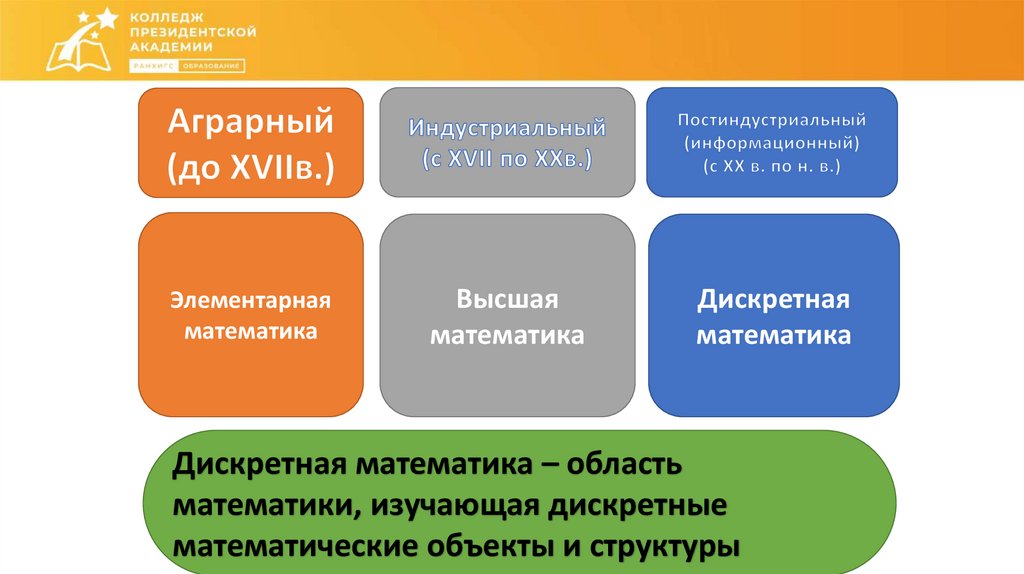
3.
Элементарнаяматематика
Высшая
математика
Дискретная
математика
Дискретная математика – область
математики, изучающая дискретные
математические объекты и структуры
4.
Основные понятия теории множествГеорг Кантор родился в СанктПетербурге в 1845 году, но с 11
лет жил в Германии. Там он
начал заниматься математикой и
сделал свои первые открытия.
Несмотря на то, что научное
сообщество
отказывалось
принимать доказательства его
концепций, сейчас он известен
как создатель теории множеств и
отец современной математики.
5.
Теория множеств и математическая логика встречаются:в аналитике
когда надо
объединить
или разделить
несколько
наборов
данных,
вычленить
один из
другого;
в программировании
когда операции над
наборами данных
надо перевести в
формальные
инструкции;
в маркетинге
когда предстоит
охватить
некоторое
множество
аудитории и
выбрать
подходящий
для этого
канал.
6.
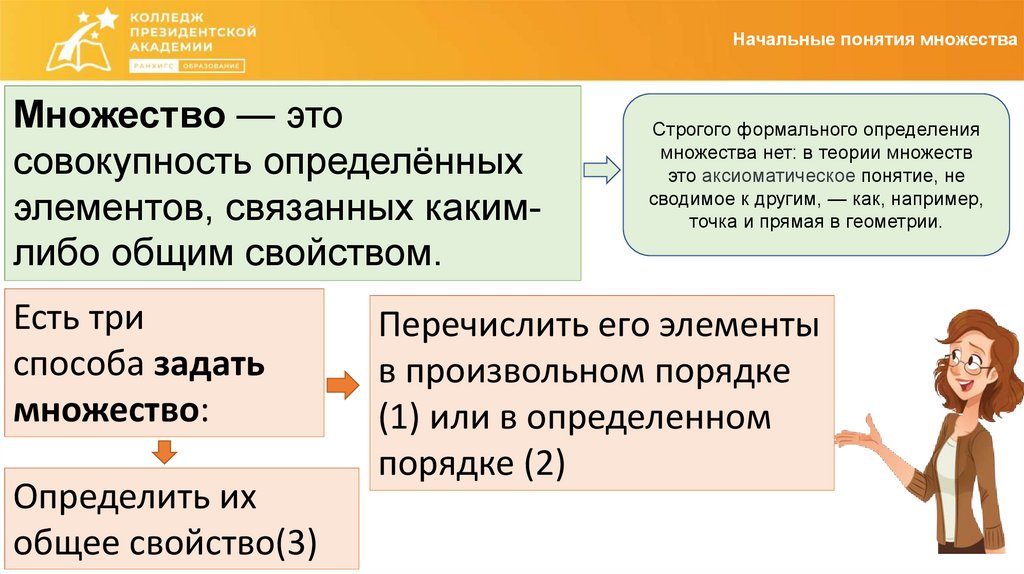
Начальные понятия множестваМножество — это
совокупность определённых
элементов, связанных какимлибо общим свойством.
Есть три
способа задать
множество:
Определить их
общее свойство(3)
Строгого формального определения
множества нет: в теории множеств
это аксиоматическое понятие, не
сводимое к другим, — как, например,
точка и прямая в геометрии.
Перечислить его элементы
в произвольном порядке
(1) или в определенном
порядке (2)
7.
8.
9.
Начальные понятия множестваМножество обозначают заглавной
буквой, а элементы множества
записывают через запятую внутри
фигурных скобок.
V={а, е, ё, и, о, у, ы, э, ю, я\}}
P={ 2,7,5,3}
P={4, 7, 5, 3}
U={у, 3, !, *, утро}
N={мандарин, оливье, елочка,
гирлянда, снег, «Ирония судьбы»}
Чтобы задать множество
перечислением, достаточно даже
одного элемента. Например, Н={3}.
10.
Элементы в записи множества не должны повторяться.11.
12.
13.
14.
15.
16.
17.
18.
19.
20.
21.
22.
23.
24.
25.
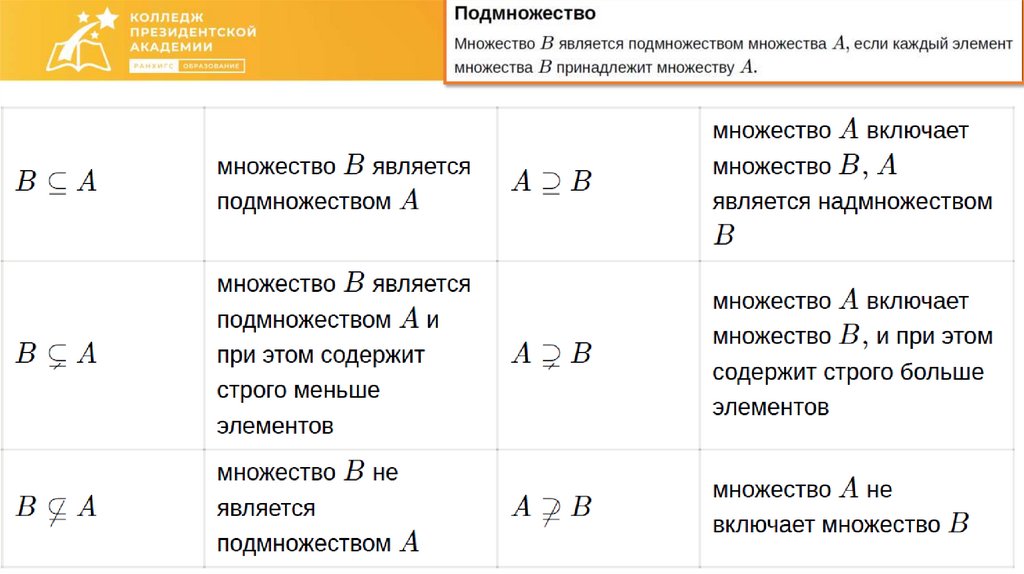
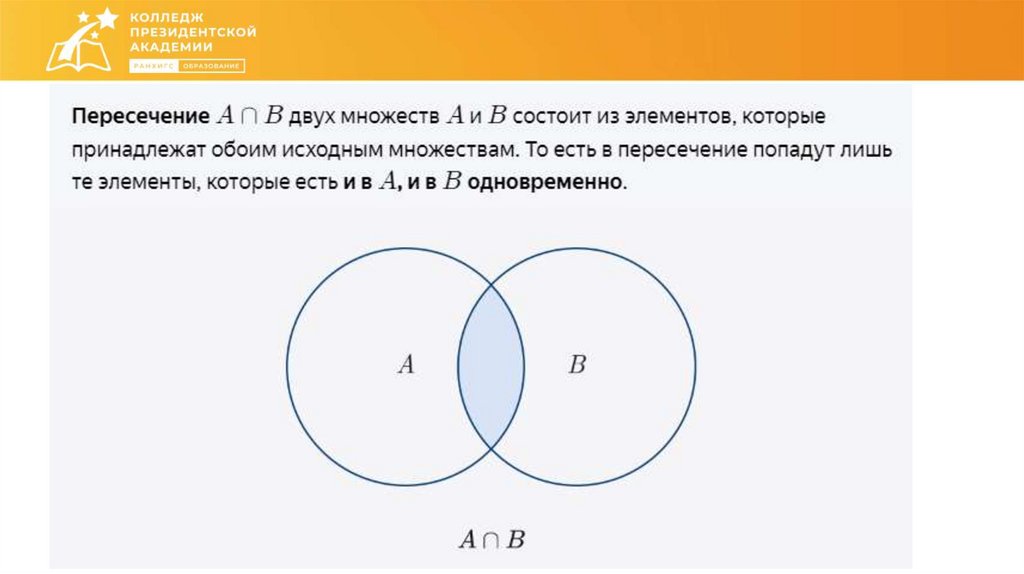
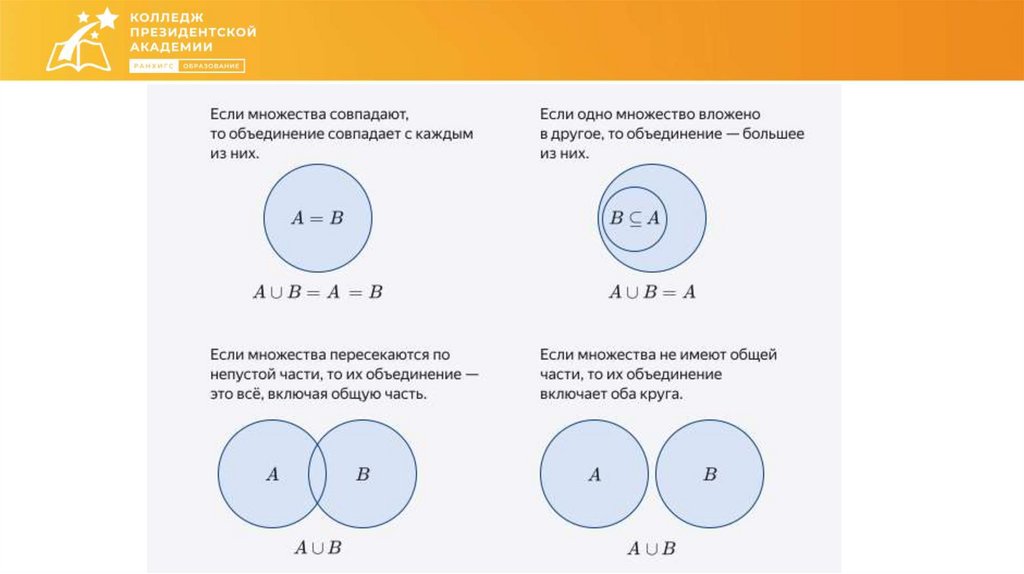
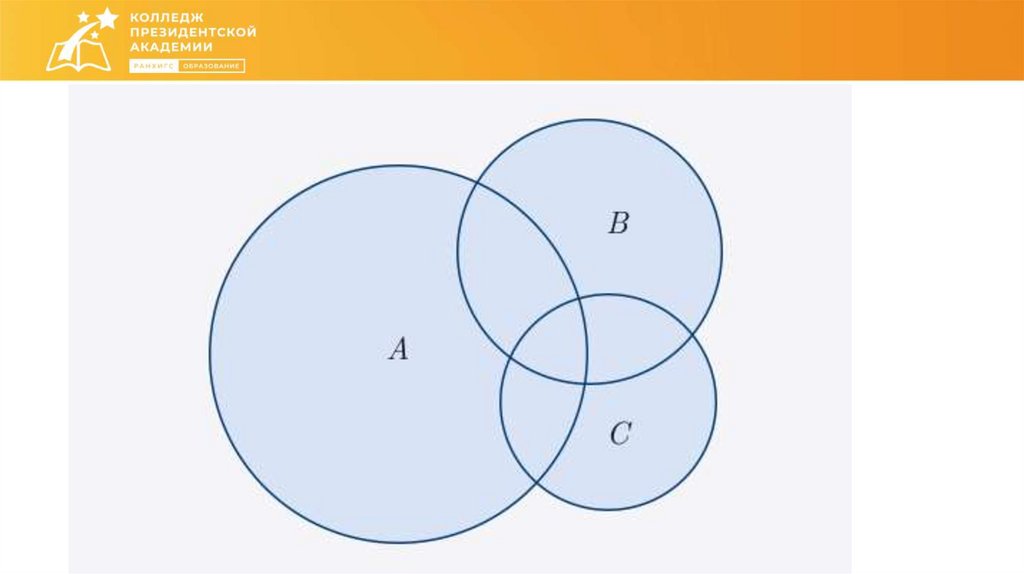
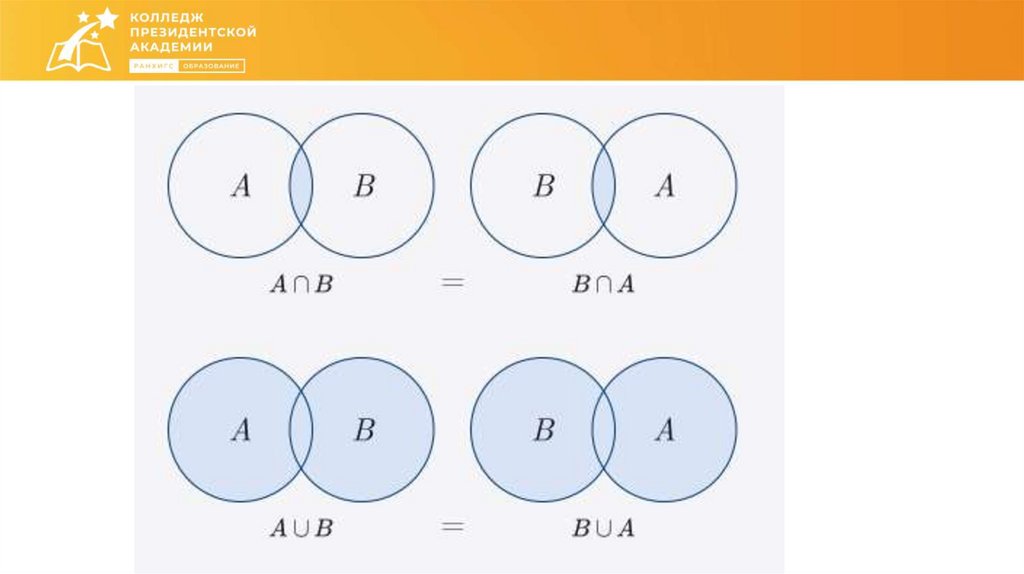
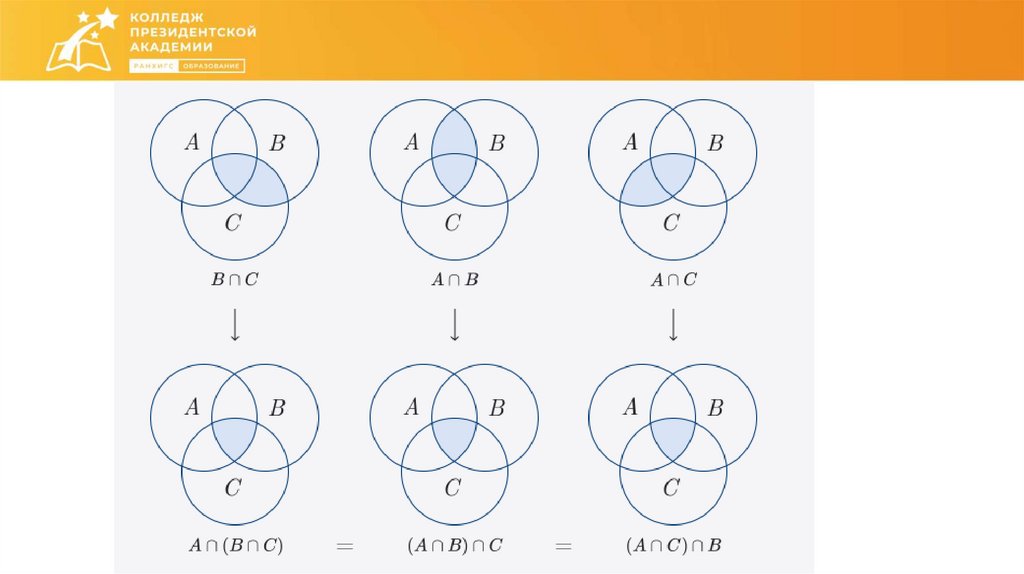
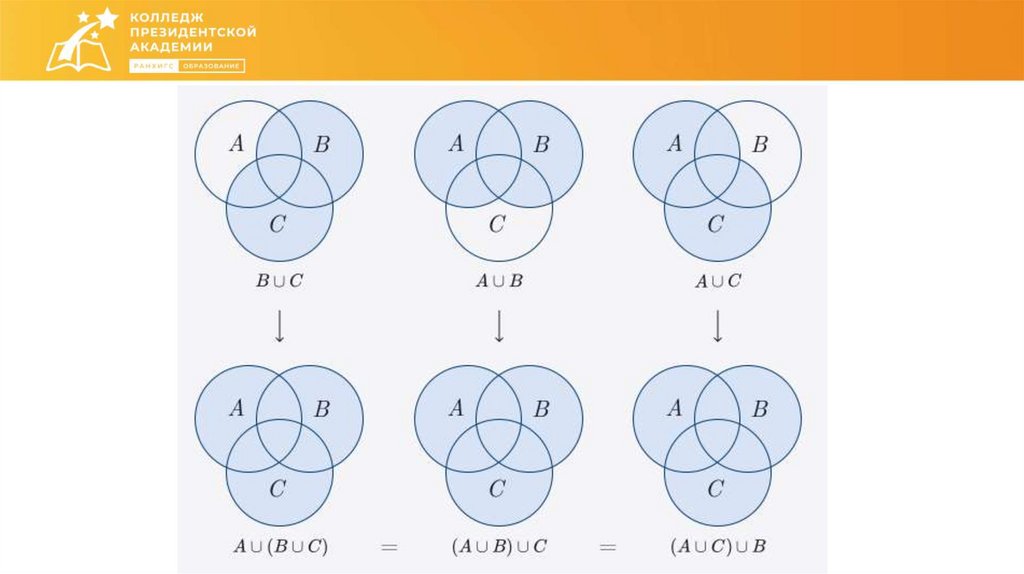
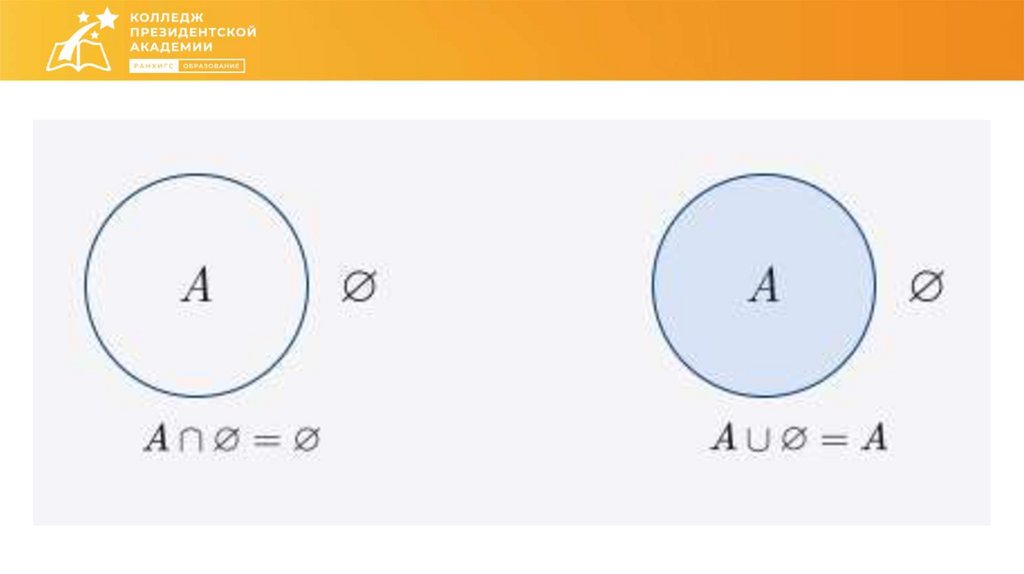
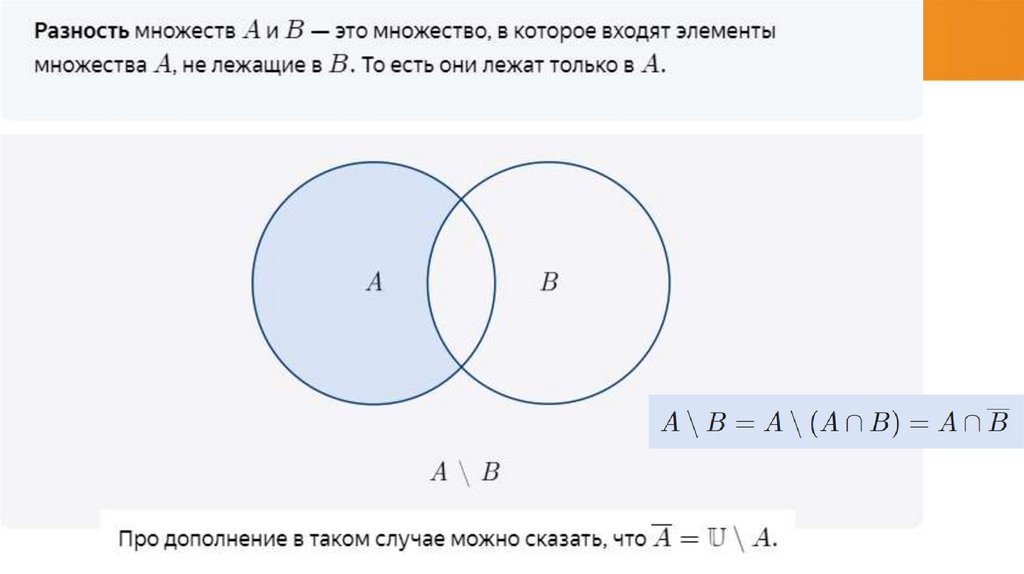
Как соотносятся друг с другом множества?26.
27.
28.
29.
30.
31.
32.
33.
34.
35.
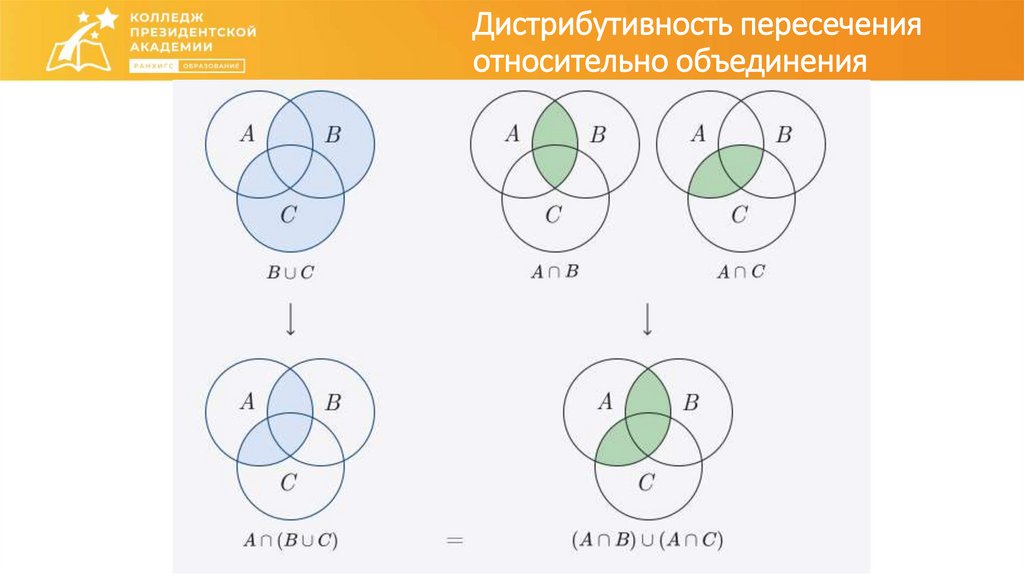
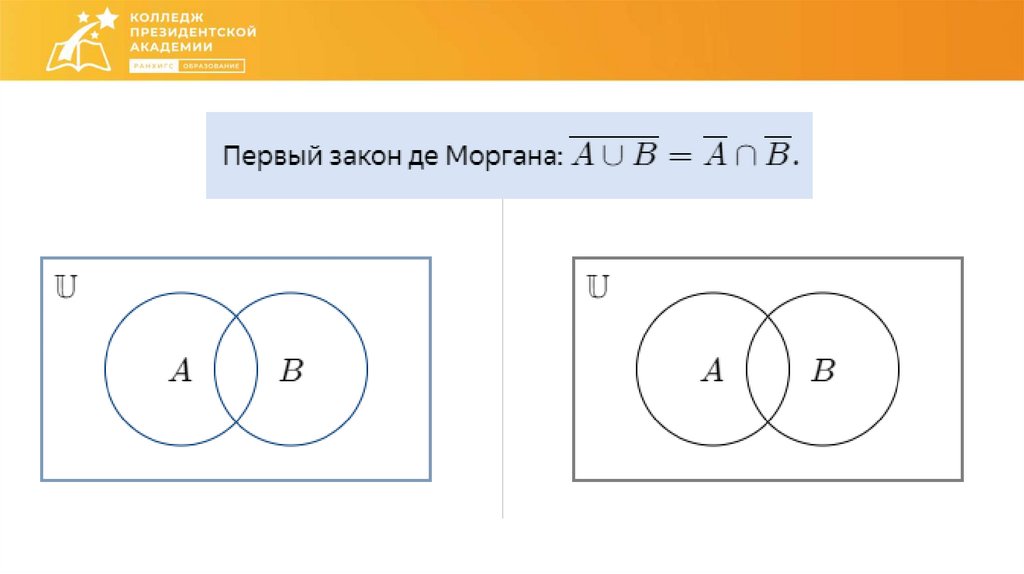
Дистрибутивность пересеченияотносительно объединения
36.
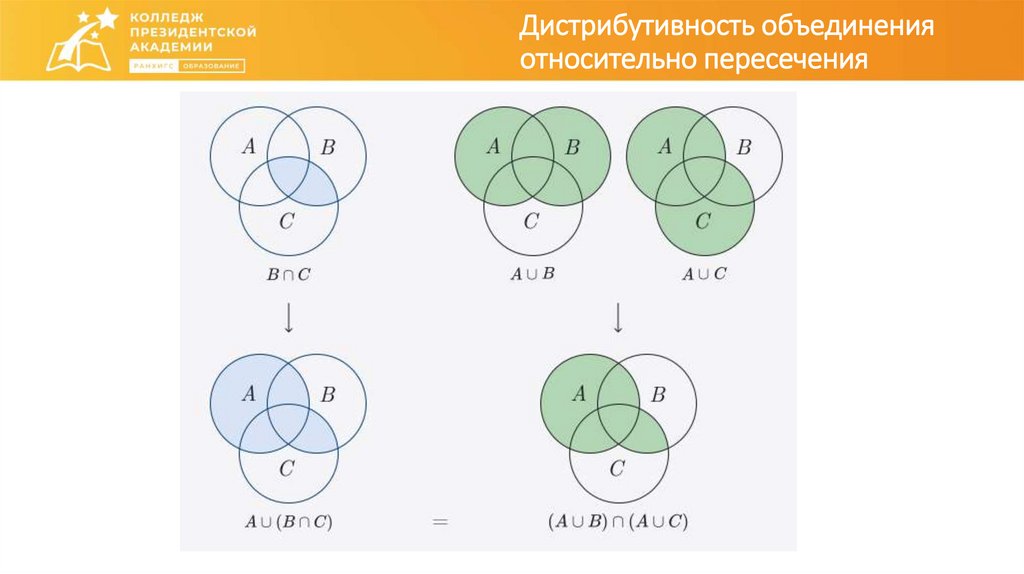
Дистрибутивность объединенияотносительно пересечения



























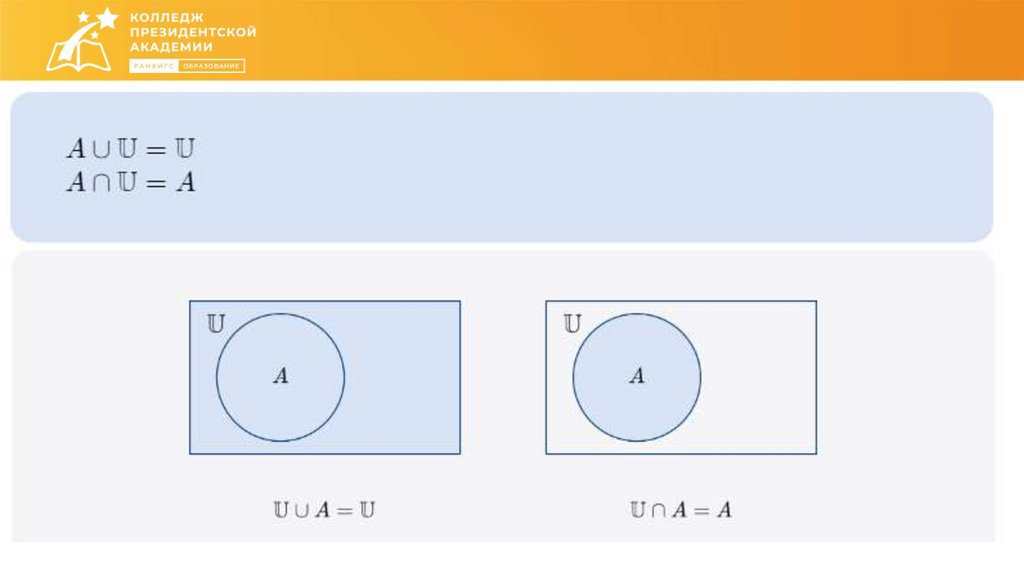


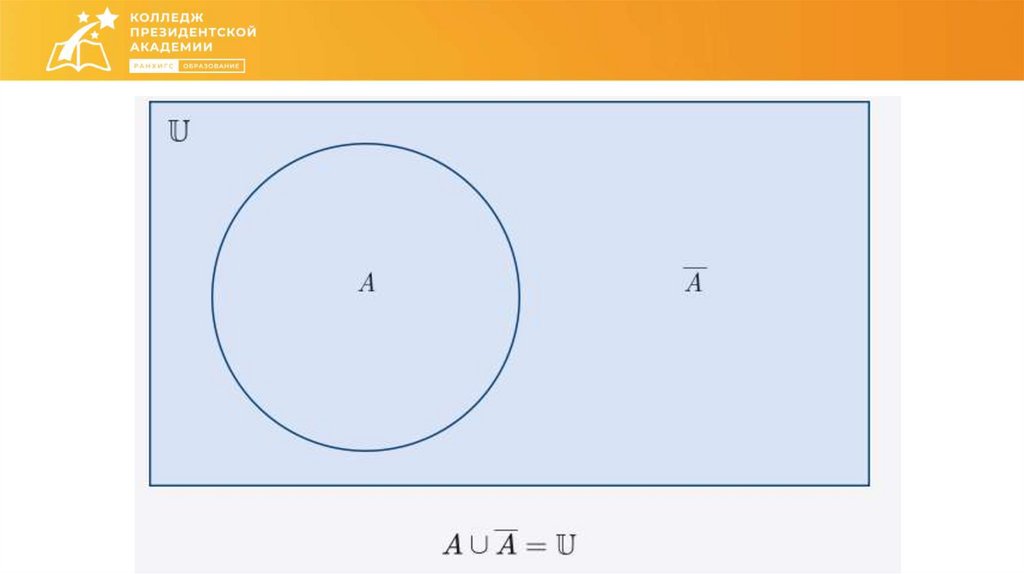
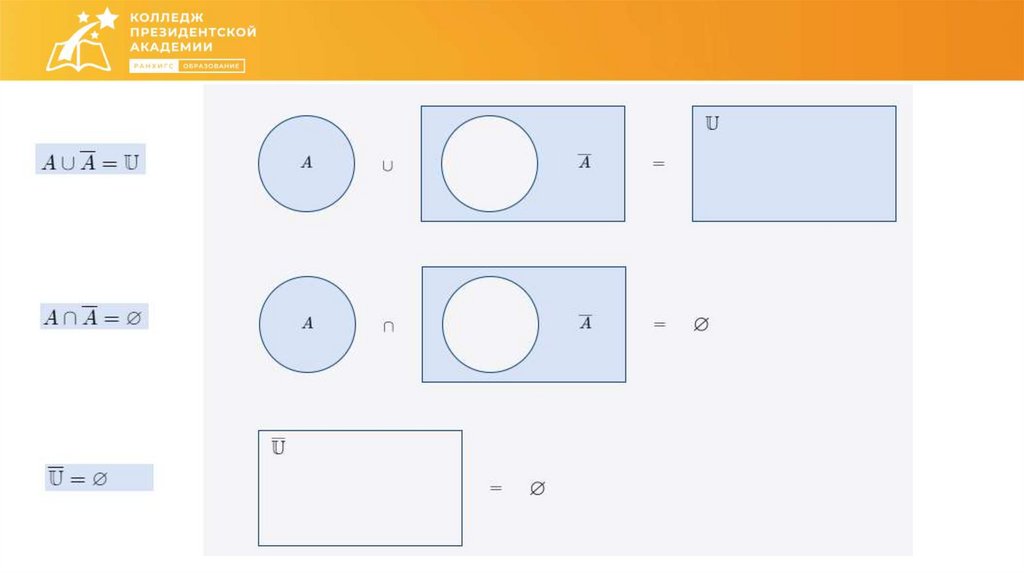
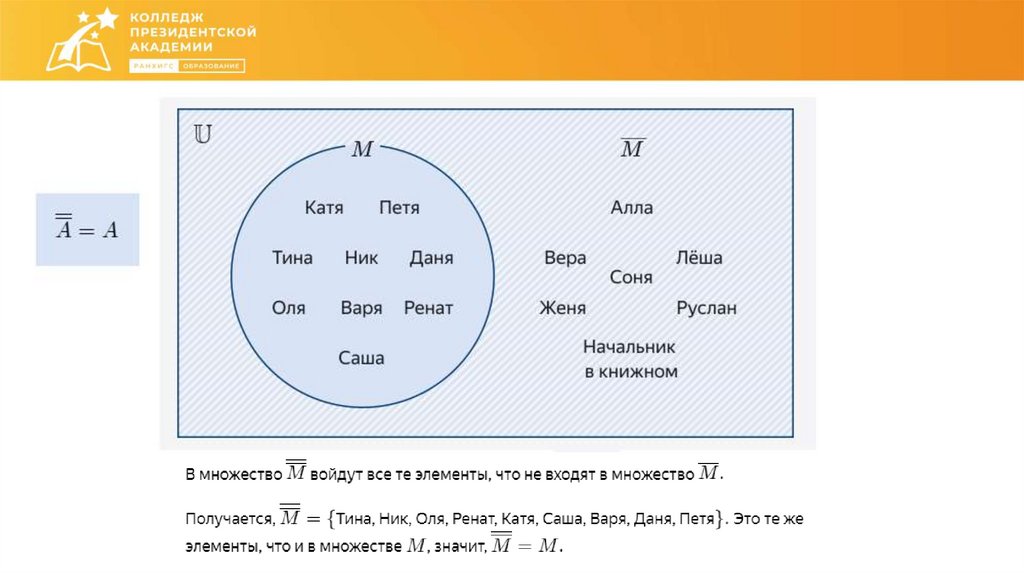












 Математика
Математика








