Похожие презентации:
Фалес Милетский Древнегреческий ученый
1.
2.
Фалес МилетскийДревнегреческий ученый
(ок. 625 – 547 гг. до н. э.)
Его именем названа
геометрическая теорема о
пропорциональных (равных)
отрезках и параллельных прямых.
Считается, что он первым сформулировал и доказал
несколько геометрических теорем, а именно:
•вертикальные углы равны;
•имеет место равенство треугольников по одной стороне и
двум прилегающим к ней углам;
•углы при основании равнобедренного треугольника
равны;
•диаметр делит круг на две равные части;
•вписанный угол, опирающийся на диаметр, является
прямым.
3.
Если параллельные прямые,пересекающие стороны
угла, отсекают на одной
его стороне равные
отрезки, то они отсекают
равные отрезки и на другой
его стороне.
4.
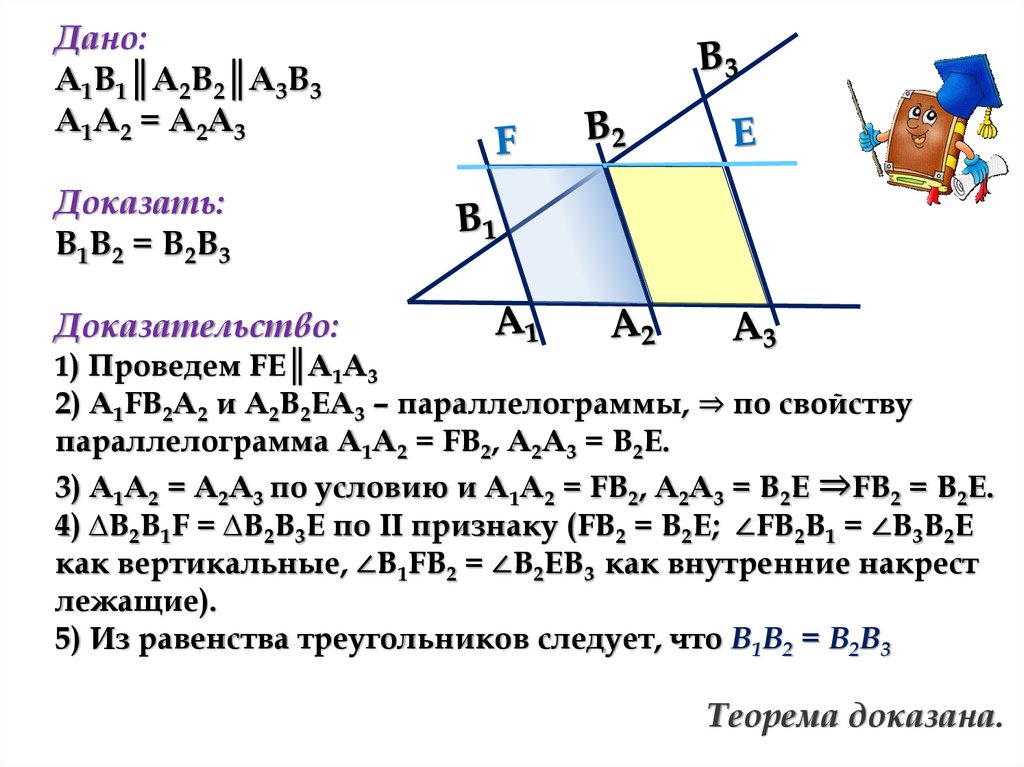
Дано:А1В1║А2В2║А3В3
А1А2 = А2А3
Доказать:
В1В2 = В2В3
Доказательство:
1) Проведем FE║А1А3
2) А1FB2A2 и A2B2EA3 – параллелограммы, ⇒ по свойству
параллелограмма А1А2 = FB2, A2A3 = B2E.
3) А1А2 = А2А3 по условию и А1А2 = FB2, A2A3 = B2E ⇒FB2 = B2E.
4) ∆В2В1F = ∆В2В3Е по II признаку (FB2 = B2E; ∠FB2B1 = ∠B3B2E
как вертикальные, ∠B1FB2 = ∠B2EB3 как внутренние накрест
лежащие).
5) Из равенства треугольников следует, что В1В2 = В2В3
Теорема доказана.
5.
Вместо сторон угла можно взять любые две прямые,тогда Параллельные прямые, пересекающие две данные
прямые и отсекающие на одной прямой равные
отрезки, отсекают на другой прямой равные отрезки.
А1
В1
А2
В2
А3
В3
А4
В4
А5
l1
В5
l2
6.
В1О
А1
В3
В2
А2
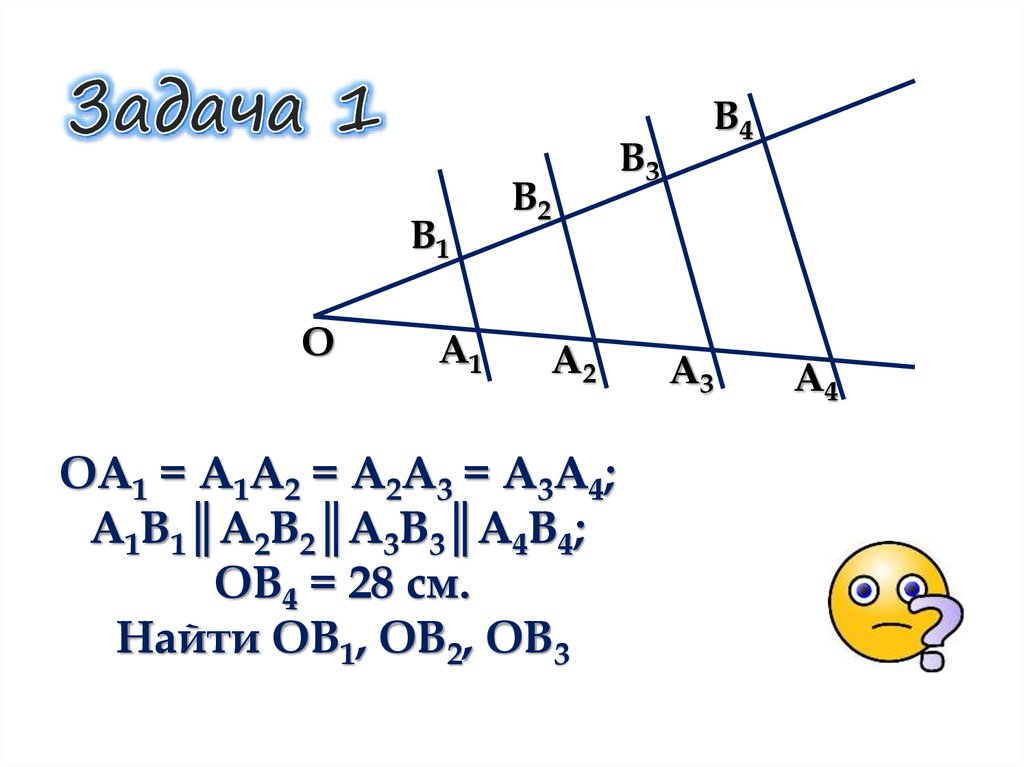
ОА1 = А1А2 = А2А3 = А3А4;
А1В1║А2В2║А3В3║А4В4;
ОВ4 = 28 см.
Найти ОВ1, ОВ2, ОВ3
В4
А3
А4
7.
Дано:АС ║ EF
Найти: P ∆АВС
B
F
E
5
4
A
12
C
8.
BДано:
АВСD – трапеция,
C МК║ВE║СD,
АD = 16 cм
10
Найти: АК
M
A
K
E
D
9.
1)2)
3) Выучить теорему Фалеса
с доказательством!








 Математика
Математика








