Движение снаряда (мины) в безвоздушном пространстве и в воздухе

1.

Тема 2: Движение снаряда
(мины) в безвоздушном
пространстве и в воздухе
Занятие 1: Сведения из
внешней баллистики

2.

Учебные вопросы:
1. Движение снаряда (мины) в
безвоздушном пространстве.
2. Движение снаряда (мины) в
воздухе.
3. Рассеивание снарядов при
ударной стрельбе.

3.

1. Предмет внешней баллистики
Баллистика - это наука, изучающая законы движения
снарядов, мин и ракет.
При изучении движения артиллерийских снарядов и
мин баллистику разделяют на два основных раздела:
внутреннюю баллистику и внешнюю.
Внутренняя баллистика изучает движение снаряда в
канале ствола.
Внешняя баллистика изучает движение снаряда от
момента вылета до окончания полета снаряда, т.е. до
попадания (падения) в цель, разрыва в воздухе и т.п.

4.

Важнейшими
являются:
задачами
внешней
баллистики
баллистическое проектирование боеприпасов и анализ
существующих артиллерийских образцов;
обработка результатов опытных стрельб;
определение дальности, высоты, скорости, времени
полета снаряда (мин, ракет), точности, кучности, меткости
стрельбы;
определение сил и моментов, действующих на снаряд в
полете;
расчеты траекторий;
оценка действующих возмущений;
составление таблиц стрельбы.
Данные внешней баллистики необходимы при
разработке многих других разделов артиллерийской
науки, таких, например, как теория стрельбы,
внутренняя
баллистика,
метеорологическое
обеспечение стрельбы и другие, а также при
составлении правил стрельбы.

5.

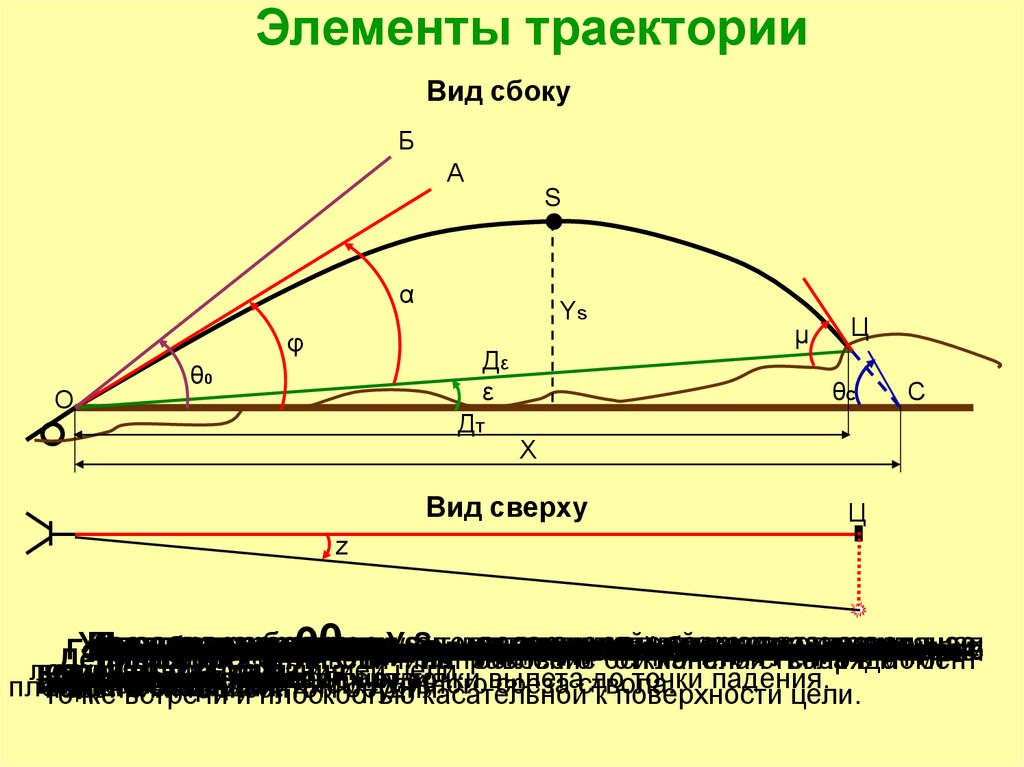
Элементы траектории
Вид сбоку
Б
А
S
α
φ
О
Ys
Дε
ε
θ0
Дт
μ
Ц
θС
С
Х
Вид сверху
Ц
z
θ
Угол
Угол
Плоскость
прицеливания
места
цели
бросания
εпадения
—
α
—
угол
—
угол
между
вертикальная
в—
вертикальной
линией
цели
плоскость,
иснаряда
горизонтом
проходящая
между
Вершина
Высота
траектории
траектории
Уs
S
—
—
расстояние
наивысшая
от
точка
горизонта
траектории
орудия
над
до
бросания
о
—
угол
между
линией
бросания
и
горизонтом
встречи
—
угол
между
касательной
кснаряда
траектории
Горизонт
Точка
вылета
орудия
О
—
горизонтальная
положение
центра
плоскость,
тяжести
проходящая
внаклонной
момент
через
Угол
падения
θ
c—
—
угол
между
касательной
кточку
траектории
виот
точке
Линия
Восходящая
Нисходящая
Табличная
Точка
Полная
Линия
Наклонная
Топографическая
возвышения
встречи
цели
выстрела
горизонтальная
точка
дальность
ОЦ
ветвь
ветвь
Цμ
—
ОА
прямая,
φ
траектории
точка,
траектории
дальность
—
—
угол
Дε
направление
проходящая
в—
С
между
которой
дальность
расстояние
OS
точка
SC
Дт
линией
—оси
—
оси
снаряд
пересечения
часть
—
через
часть
канала
по
выстрела
проекция
Xплоскости
траектории
линии
встречает
траектории
—
ствола
вылета
цели
траектории
иизмеренное
цель
от
от
точки
точки
или
ее
св
Деривация
Линия
бросания
Z
—
величина
ОБ
—
направление
бокового
отклонения
канала
ствола
в
момент
от
линией
орудия.
через
линию
выстрела
бросания.
и падения.
линией
горизонтом
вершины
траектории.
орудия.
цель.
вылета
вершины
горизонтом
преграду.
расстояние
наведенного
горизонтом
вылета
дальности
до
до
до
ее
цели.
на
орудия.
по
орудия.
точки
орудия.
вершины.
горизонт
горизонту
орудия.
отцели.
точки вылета
до точки падения.
орудия.
точку
прохождения
вылета.
его
дном
дульного
среза ствола.
плоскости
вылета
снаряда.
бросания.
падения
и
горизонтом
орудия.
точке встречи и плоскостью касательной
к поверхности цели.

6.

Точка вылета О — положение центра тяжести снаряда в момент
прохождения его дном дульного среза ствола.
Горизонт орудия — горизонтальная плоскость, проходящая через
точку вылета.
Линия выстрела ОА — направление оси канала ствола
наведенного орудия.
Линия бросания ОБ — направление оси канала ствола в момент
вылета снаряда.
Линия цели ОЦ — прямая, проходящая через точку вылета и
цель.
Угол прицеливания α — угол в вертикальной плоскости между
линией выстрела и линией цели.
Угол возвышения φ — угол между линией выстрела и
горизонтом орудия.
Угол бросания θо — угол между линией бросания и горизонтом
орудия.
Угол места цели ε — угол между линией цели и горизонтом
орудия.
Плоскость бросания — вертикальная плоскость, проходящая
через линию бросания.

7.

Вершина траектории S — наивысшая точка траектории над
горизонтом орудия.
Высота траектории Уs — расстояние от горизонта орудия до
вершины траектории.
Восходящая ветвь траектории OS — часть траектории от точки
вылета до ее вершины.
Нисходящая ветвь траектории SC — часть траектории от ее
вершины до точки падения.
Табличная точка падения С — точка пересечения траектории с
горизонтом орудия.
Точка встречи Ц — точка, в которой снаряд встречает цель или
преграду.
Наклонная дальность Дε — расстояние по линии цели от точки
вылета до цели.
Угол встречи μ
— угол между касательной к траектории в
точке встречи и плоскостью касательной к поверхности цели.
Топографическая дальность Дт — проекция наклонной
дальности на горизонт орудия.
Полная горизонтальная дальность X — измеренное
расстояние по горизонту от точки вылета до точки падения.

8.

Деривация Z — величина бокового отклонения снаряда от
плоскости бросания.
Начальная скорость V0 — скорость снаряда в точке вылета.
Окончательная скорость Vc — скорость снаряда в табличной
точке падения.
Полное время полета снаряда tc — время движения снаряда от
точки вылета до табличной точки падения.
Угол падения θc — угол между касательной к траектории в точке
падения и горизонтом орудия.

9. Понятие о деривации

10.

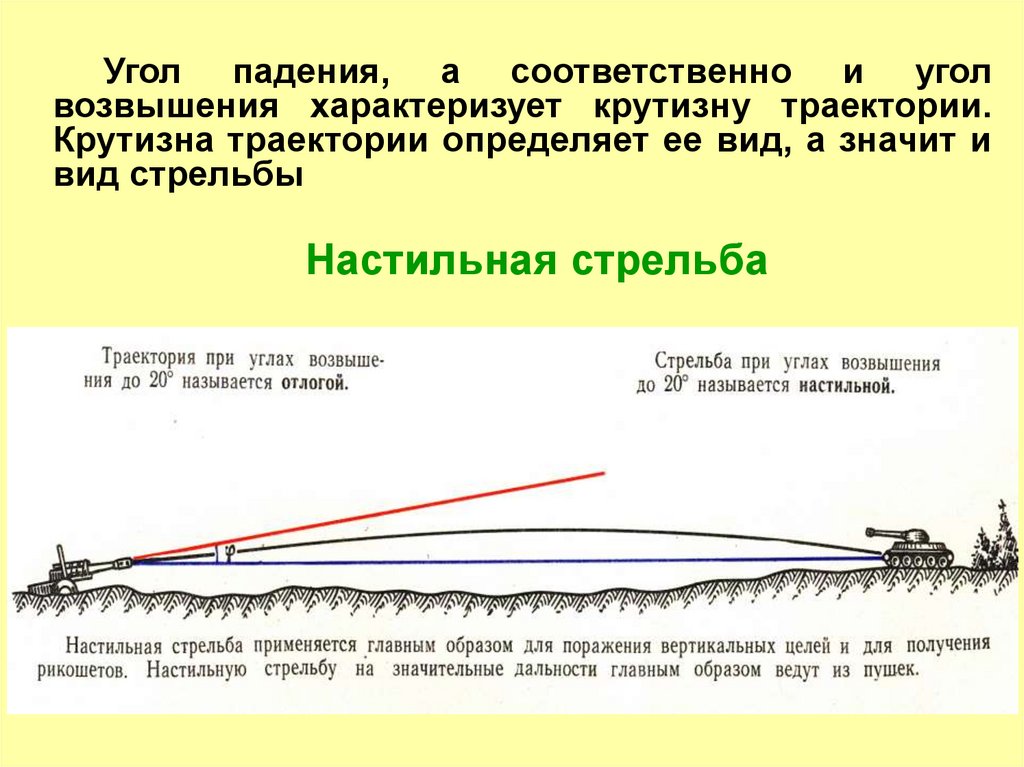
Угол падения, а соответственно и угол
возвышения характеризует крутизну траектории.
Крутизна траектории определяет ее вид, а значит и
вид стрельбы
Настильная стрельба

11.

Навесная стрельба

12.

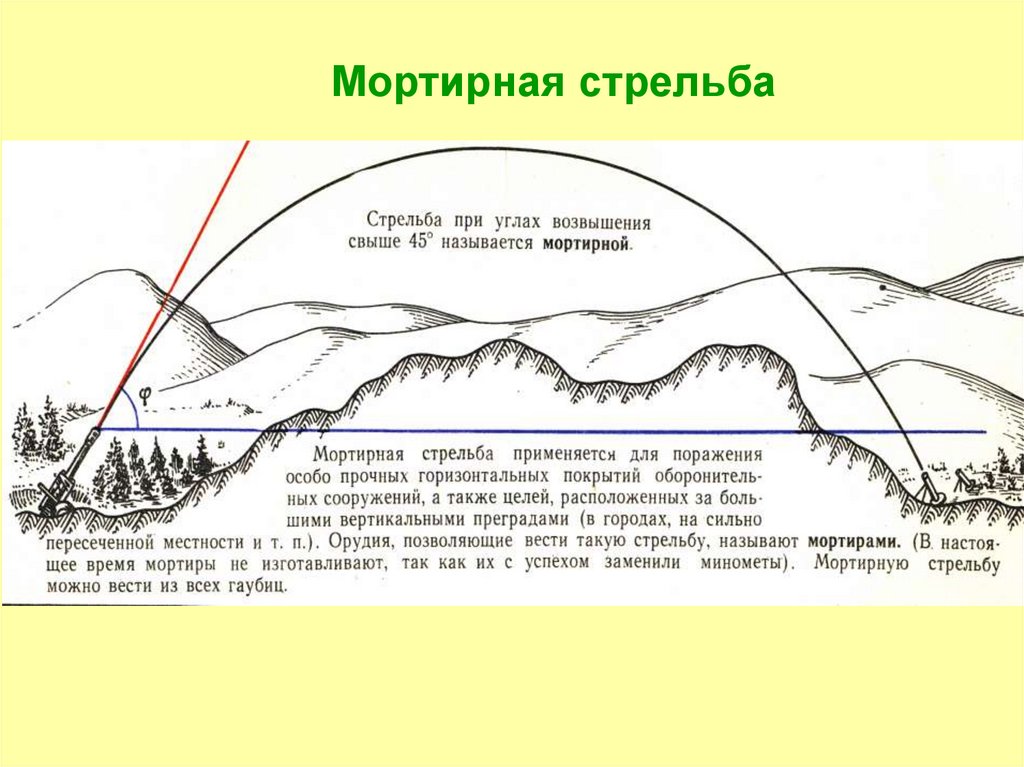
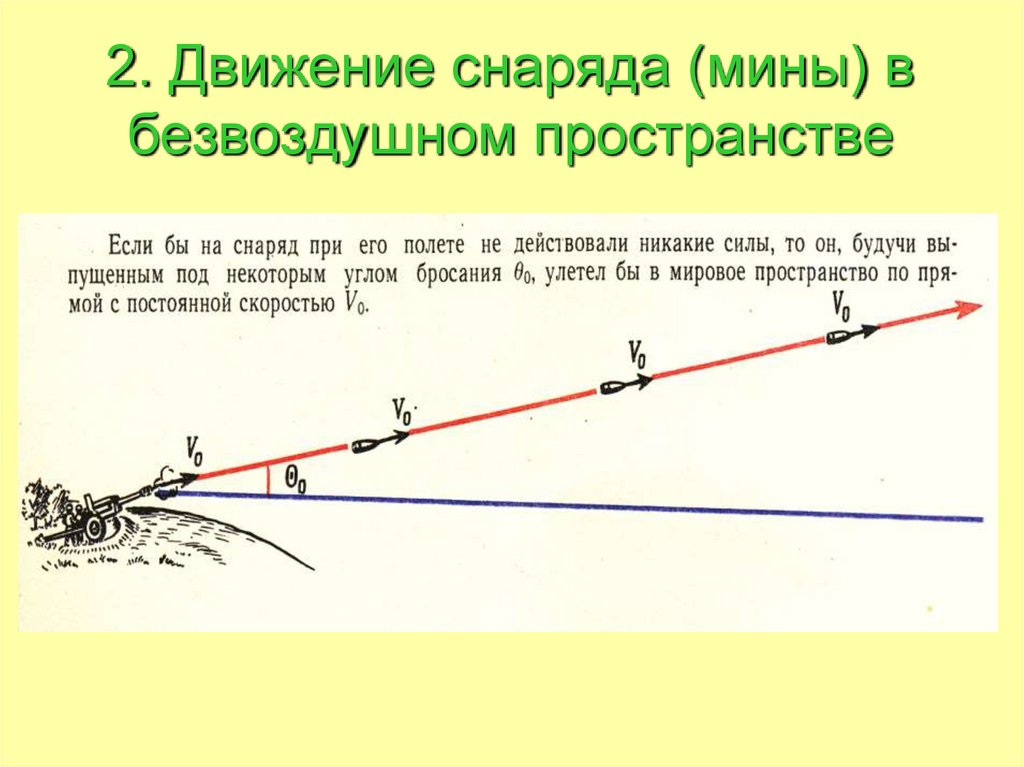
Мортирная стрельба

13. 2. Движение снаряда (мины) в безвоздушном пространстве

14.

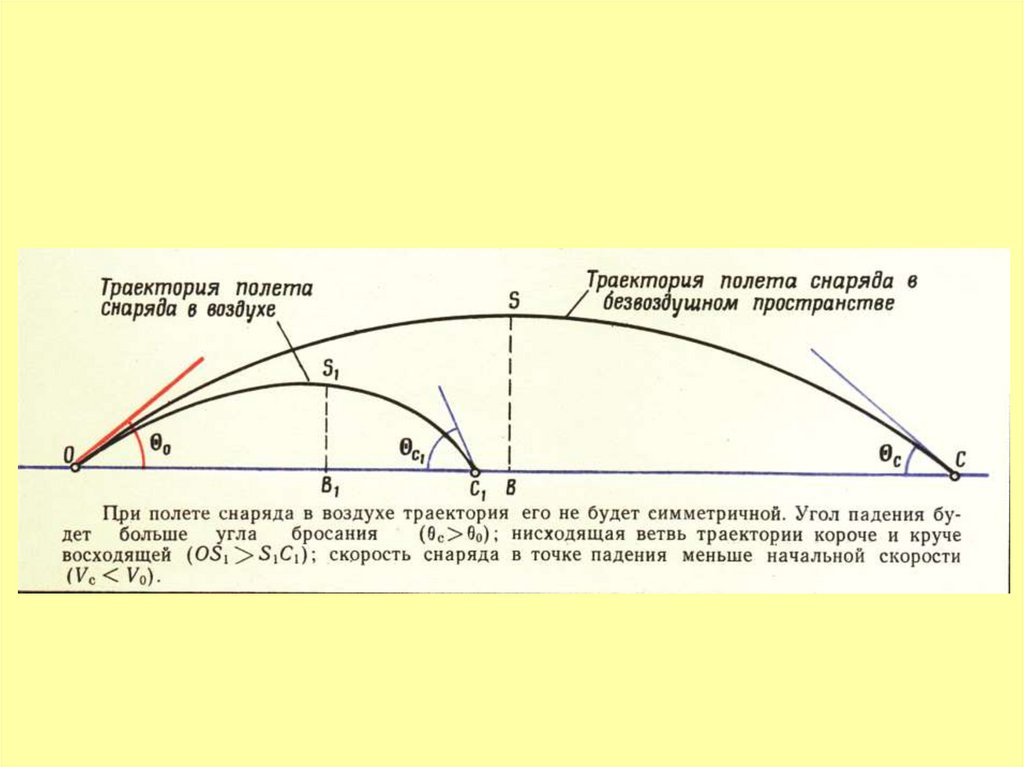
15. 3. Движение снаряда (мины) в воздухе

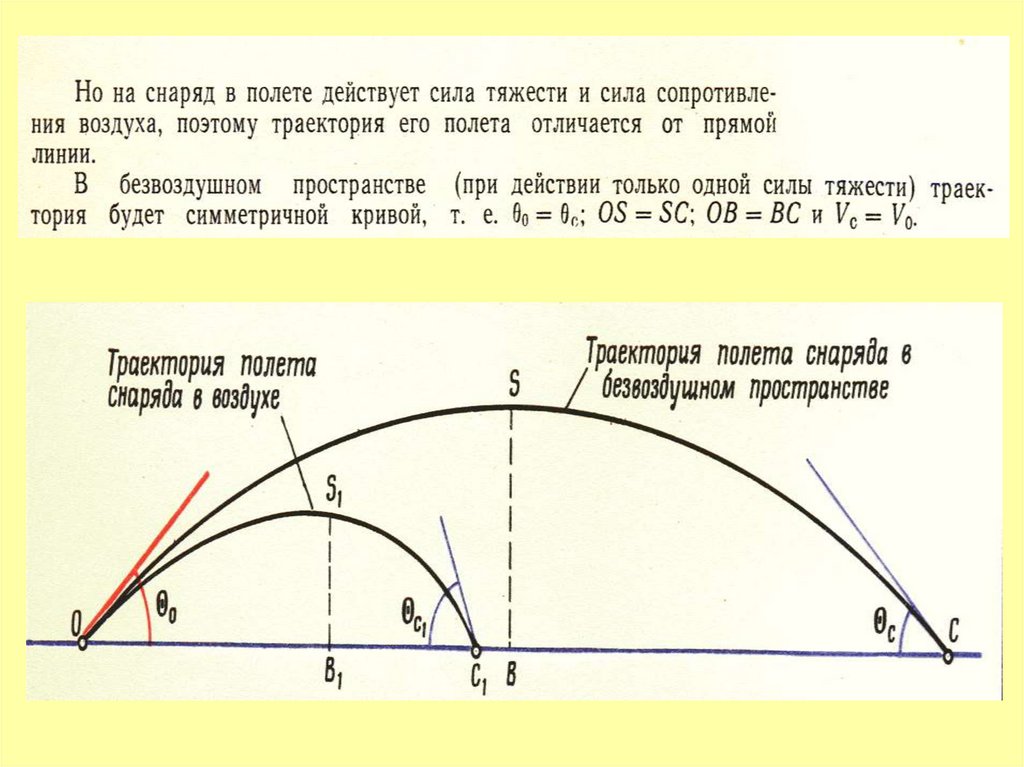
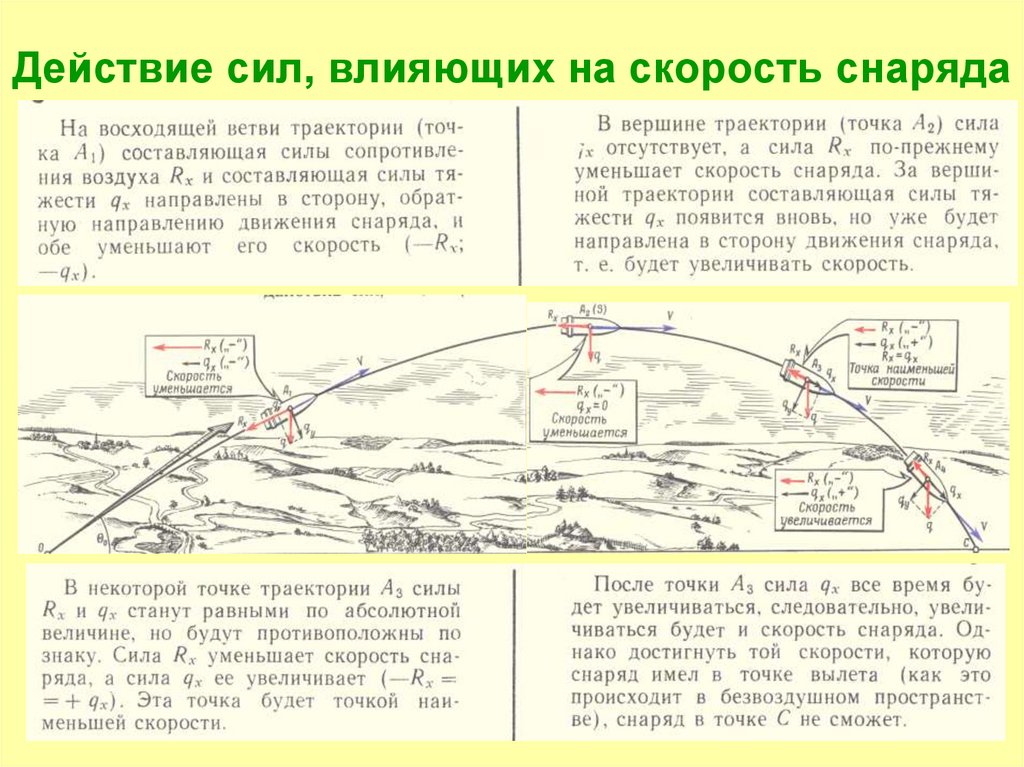
В воздухе на полет снаряда действуют две основные
силы: сила тяжести и сила сопротивления воздуха.
Рассмотрим действие силы тяжести.
1. На восходящей ветви траектории

16.

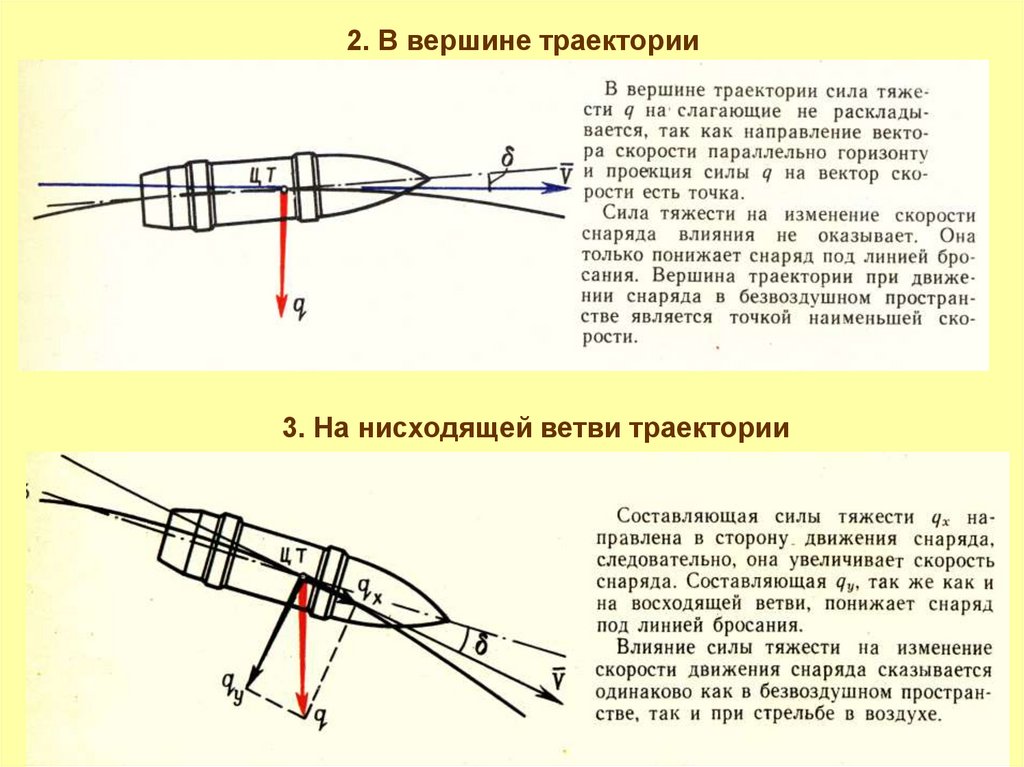
2. В вершине траектории
3. На нисходящей ветви траектории

17.

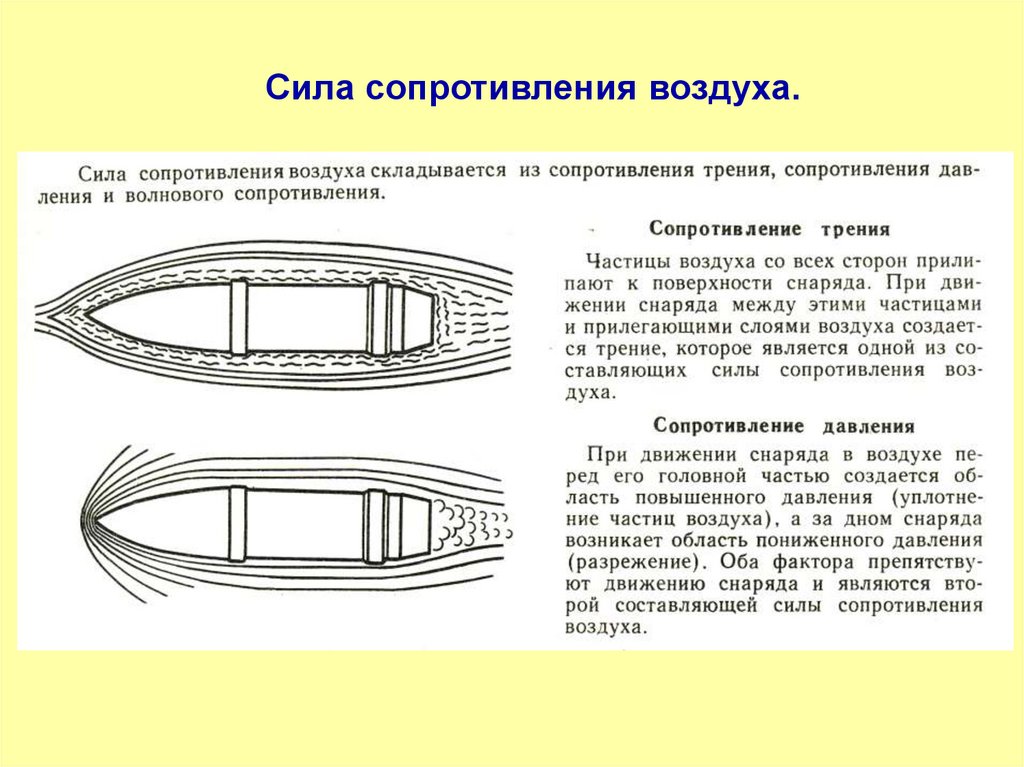
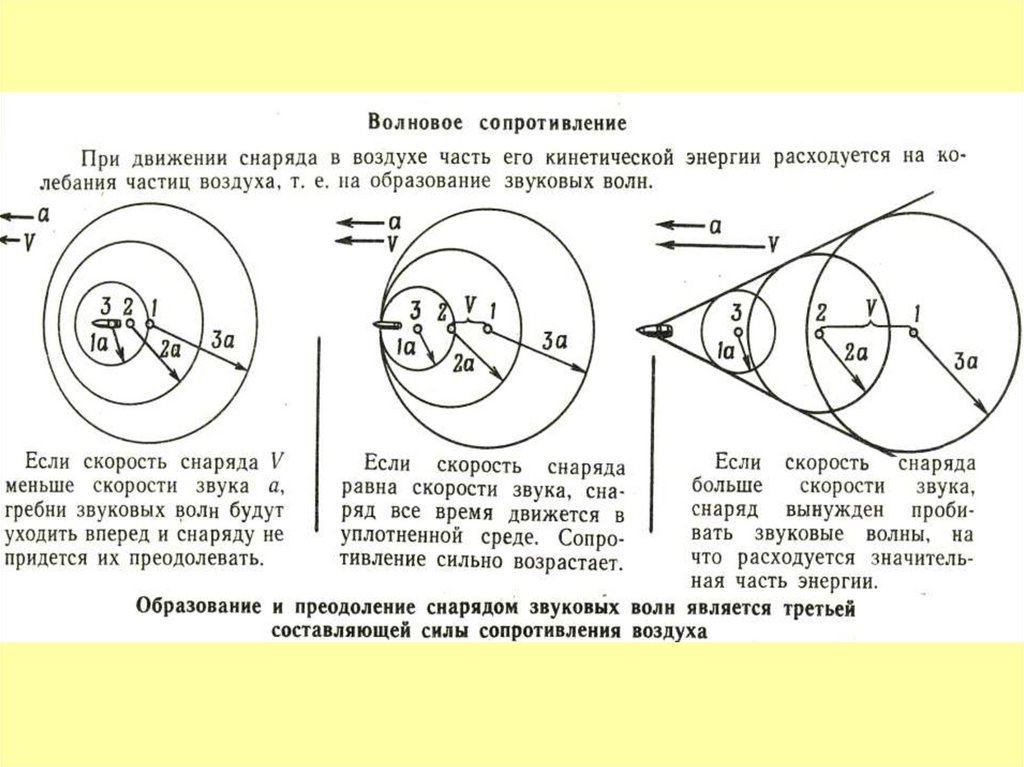
Сила сопротивления воздуха.

18.

19. Действие сил, влияющих на скорость снаряда

20.

21. 3. Рассеивания снарядов, при ударной стрельбе.

22.

При стрельбе по цели из одного и того же орудия
в возможно одинаковых условиях можно заметить,
что разрывы снарядов происходят не в одной точке,
а рассеиваются на некоторой площади, называемой
площадью рассеивания.
Явление разброса точек падения снарядов при
стрельбе из одного и того же орудия в возможно
одинаковых условиях называется рассеиванием
снарядов.
Рассеивание снарядов зависит от многих причин,
которые можно свести в три группы:
разнообразие начальных скоростей;
разнообразие углов бросания и направлений
стрельбы;
разнообразие условий полета снаряда после
вылета из орудия.

23.

Разнообразие начальных скоростей вызывается
действием
ряда
причин.
При
производстве
неизбежны допуски в технологии изготовления
пороха, приводящие к различию химического состава
пороха. Невозможно добиться и однообразия в массе
зарядов, на огневых позициях не представляется
возможным обеспечить абсолютно одинаковые
условия хранения зарядов, а это приводит к
различию температуры каждого заряда.
К изменениям начальной скорости при каждом
выстреле приводят, кроме того, неодинаковые досыл
снаряда и различия в массе снарядов.
Разнообразие углов бросания и направлений
стрельбы является следствием случайных ошибок в
установках прицела, уровня, угломера и в наведении
орудия, а также ошибок из-за неодинакового выбора
мертвых ходов механизмов орудия.

24.

Разнообразие условий полета снарядов после
вылета
из
орудия
вызывается
изменениями
метеорологических условий, происходящими во время
полета каждого снаряда. Эти изменения не могут быть
заранее учтены. Вследствие этого каждый снаряд
летит по своей траектории. Кроме того, разнообразие в
форме, массе снарядов и положении их центров
тяжести приводит к изменению силы сопротивления
воздуха при полете каждого снаряда.
В действительных условиях стрельбы при каждом
выстреле действуют все три группы причин
рассеивания траекторий, вследствие чего один снаряд
летит дальше, другие ближе, одни правее, другие
левее, т.е. полет каждого снаряда происходит по
траектории, отличающейся от траектории других
снарядов.

25.

Совокупность всех траекторий, какие могут быть
получены при стрельбе из данного орудия в данных
условиях, называется снопом траекторий.
Воображаемая траектория, проходящая в середине
снопа траекторий, называется средней траекторией.
Точка
пересечения
средней
траектории
с
горизонтом орудия называется средней точкой
падения или центром рассеивания снарядов и
обозначается буквой С.
О
С

26.

Рассеивание снарядов – явление неизбежное, но
это не означает, что мы не можем влиять на его
величину. Анализ причин рассеивания снарядов
показывает, что значительная часть из них зависит
от правильного хранения, сбережения и подготовки
орудий, орудийных расчетов по выполнению своих
обязанностей.
Основные меры, которые необходимо принимать
для уменьшения рассеивания, сводятся к следующему:
все механизмы орудия необходимо тщательно
отрегулировать в строгом соответствии с требованиями
Инструкции по эксплуатации;
орудие
необходимо
устанавливать
на
горизонтальной площадке и надежно укреплять в
грунте;
нужно выбирать достаточно удаленную, устойчивую,
хорошо видимую точку наводки;

27.

наводчики должны тщательно и однообразно
производить установку прицела, уровня и угломера,
тщательно производить наводку, восстанавливать ее
перед каждым выстрелом и принимать меры по
устранению влияния мертвых ходов механизмов;
заряжающие
должны однообразно досылать
снаряды;
не
рекомендуется
держать
орудия
долго
заряженными;
тщательно проводить сортировку зарядов по
партиям, снарядов по партиям и знакам отклонения
массы, тщательно очищать снаряды от смазки;
огневую задачу следует выполнять зарядами одной
партии и желательно снарядами одной партии с
одними и теми же знаками отклонения массы;
заряды
необходимо
хранить
в одинаковых
температурных условиях;
строго соблюдать установленный режим огня.

28. Закон рассеивания и его характеристики

Многие из причин, вызывающих рассеивание
снарядов,
связаны
со
случайными
ошибками
различного рода измерений. Некоторые из причин не
связаны с измерениями (подпрыгивание орудия,
неоднородность химического состава заряда и т.д.),
однако влияние их также случайно. Отклонение каждой
точки падения снарядов от центра рассеивания
снарядов случайно и может быть представлена как
результат действия большого числа элементарных
ошибок очень мала по сравнению с суммарной
величиной отклонения данной точки падения снарядов.
Поэтому можно заключать, что рассеивание снарядов
характеризуется нормальным законом.
Закон рассеивания выражает зависимость между
величиной отклонения снаряда от центра рассеивания
и вероятностью этого отклонения следующими тремя
положениями:

29.

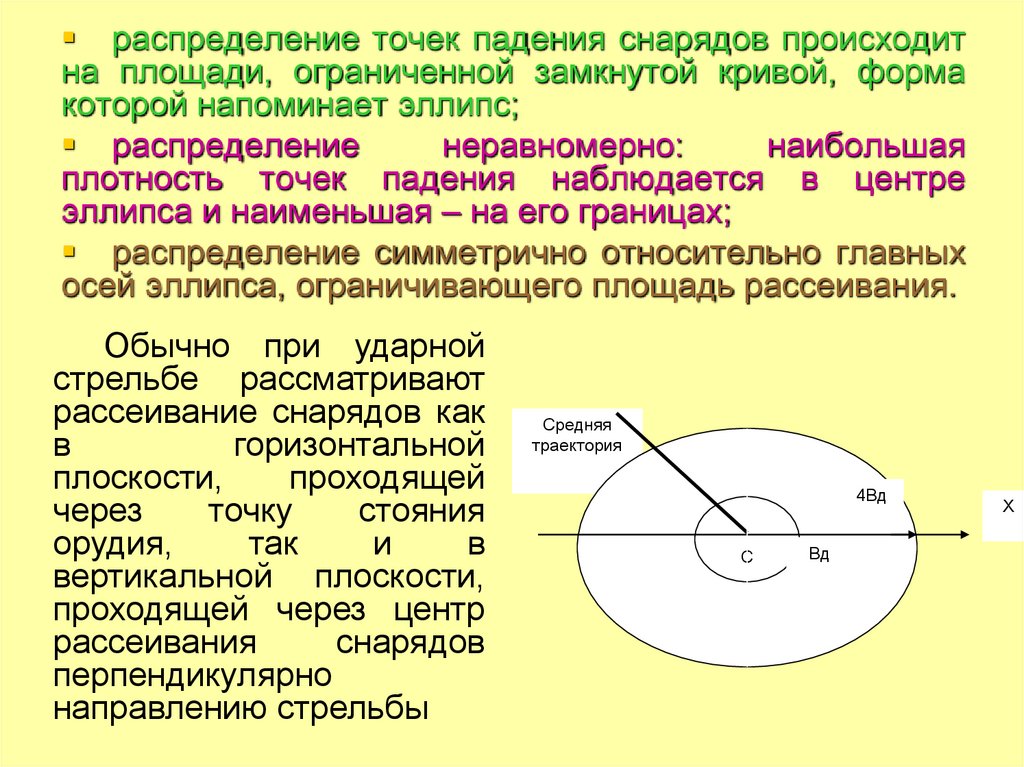
распределение точек падения снарядов происходит
на площади, ограниченной замкнутой кривой, форма
которой напоминает эллипс;
распределение
неравномерно:
наибольшая
плотность точек падения наблюдается в центре
эллипса и наименьшая – на его границах;
распределение симметрично относительно главных
осей эллипса, ограничивающего площадь рассеивания.
Обычно при ударной
стрельбе рассматривают
рассеивание снарядов как
в
горизонтальной
плоскости,
проходящей
через
точку
стояния
орудия,
так
и
в
вертикальной плоскости,
проходящей через центр
рассеивания
снарядов
перпендикулярно
направлению стрельбы
Средняя
траектория
4Вд
С
Вд
Х

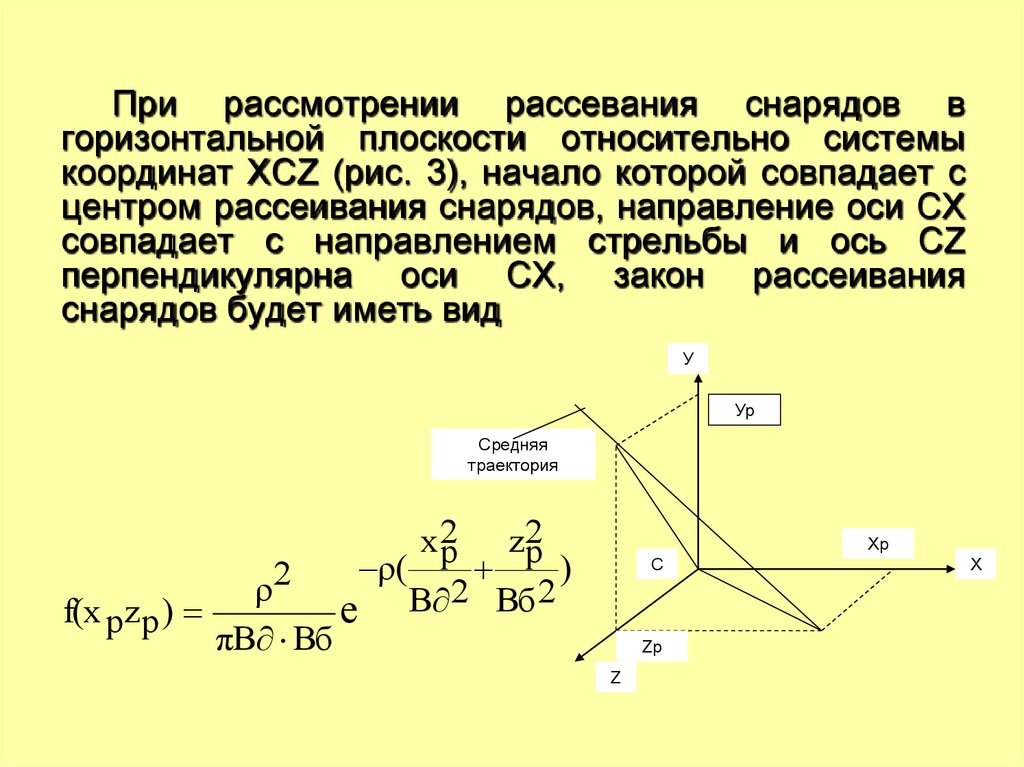
30.

При рассмотрении рассевания снарядов в
горизонтальной плоскости относительно системы
координат ХСZ (рис. 3), начало которой совпадает с
центром рассеивания снарядов, направление оси СХ
совпадает с направлением стрельбы и ось СZ
перпендикулярна оси СХ, закон рассеивания
снарядов будет иметь вид
У
Ур
Средняя
траектория
f(x pz p )
ρ2
πВ Вб
е
х2
z2
р
ρ(
р )
В 2 Вб 2
Хр
С
Zр
Z
Х

31.

Значения В∂ и Вб приводятся в таблицах
стрельбы,
из рассмотрения которых можно
установить,
что
величина
характеристики
рассеивания снарядов увеличивается с увеличением
дальности стрельбы.
При стрельбе из минометов и систем реактивной
артиллерии в ряде случаев рассеивание снарядов
может быть круговым. В этом случае боковое
рассеивание равно рассеиванию по дальности.
В практике пределы рассеивания снарядов
обычно принимают равными четырем срединным
отклонениям от центра рассеивания по каждому
направлению (±4В∂, ±4Вб). Для теоретических
расчетов пределы рассеивания иногда берут
равными пяти-шести срединным отклонениям.

32.

Используя формулу Р = (Хп<Х<Хт) = ½ [Ф (β2) – Ф (β1)]
где β2 Хm mх ;
Вд
β
1
Хn mх
Вд
центрированные границы участка, выраженные в Вд
можно рассчитать вероятности получения разрывов в
различных интервалах, выраженных в В∂ или Вб. В
результате таких расчетов получают шкалу рассеивания
снарядов по дальности, направлению или по высоте.

33. 3. Шкала рассеивания и ее использование

Таблица показывает шкалу рассеивания по
дальности. Шкала рассеивания численно выражает
собой закон рассеивания снарядов по данному
направлению. Шкала рассеивания по направлению и
по высоте подобна шкале, показанной в таблице.
Средняя
траектория
-4 В∂
-3В∂
0,02
0,005
0,015
-2В∂
0,07
0,03
0,04
-1В∂
0,16
0,07
0,09
+1В∂
0
0,25
0,12
0,13
0,25
0,13
0,12
+2В∂
0,16
0,009
0,007
+3В∂
0,07
0,004
0.003
+4В∂
0,02
0,015
0,005

34.

Пример 2.1. При стрельбе на одних и тех же
установках при четырех выстрелах по цели, размеры
которой по фронту значительно больше 8 Вб, получено
три недолета и один перелет. Цель расположена
перпендикулярно направлению стрельбы. Определить
величину отклонения центра рассеивания снарядов по
дальности от цели.
По
шкале
рассеивания
можно
определить
вероятность
заданного отклонения (вероятность
полпадания в цель), а также решать обратную задачу –
по количеству перелетов и недолетов определять
примерное отклонение центра рассеивания снарядов
от цели. Зная величину отклонения, можно изменить
установку прицельных приспособлений на эту величину
для совмещения центра рассеивания снарядов с
целью.

35.

Средняя
траектория
-4
0,02
-3
0,07
-2
0,16
-1
Недолетов
Хт
0,25
0
0,25
+1
0,16
+2
0,07
+3
0,02
+4
Перелетов
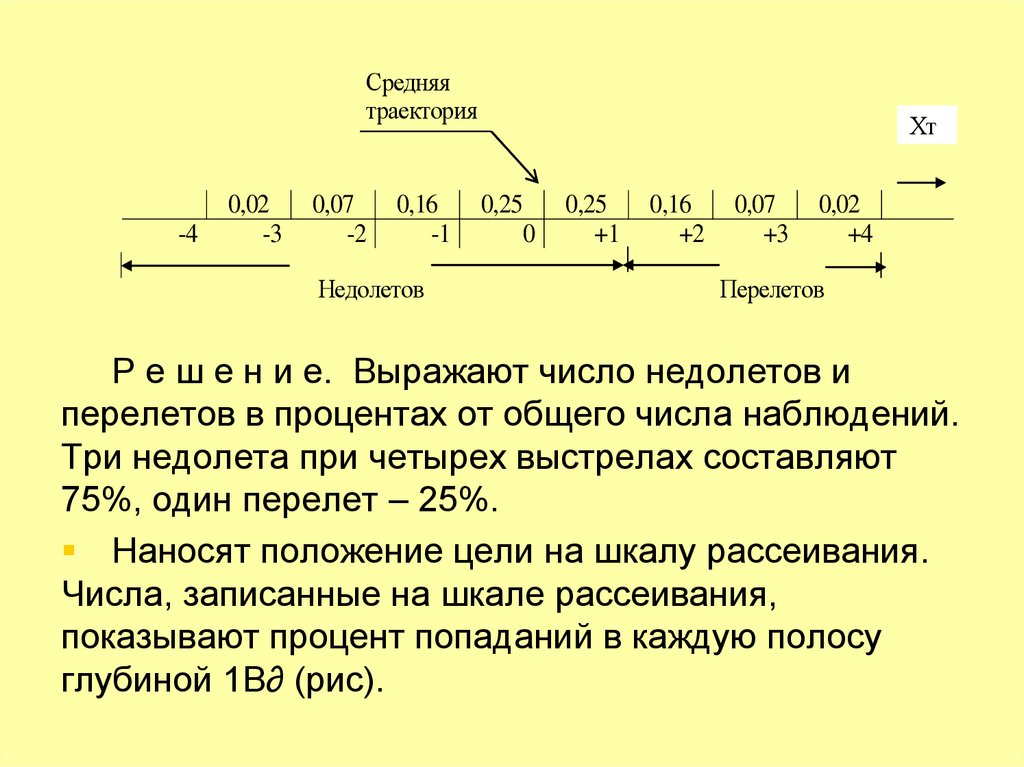
Р е ш е н и е. Выражают число недолетов и
перелетов в процентах от общего числа наблюдений.
Три недолета при четырех выстрелах составляют
75%, один перелет – 25%.
Наносят положение цели на шкалу рассеивания.
Числа, записанные на шкале рассеивания,
показывают процент попаданий в каждую полосу
глубиной 1В∂ (рис).

36.

25% перелетов выражают сумму цифр процентов
попадания в три правые полосы. 75% недолетов
выражает сумма цифр процентов попадания в левые
пять полос (стрельба слева).
Делают вывод о величине отклонения центра
рассеивания снарядов от цели и о величине
корректуры.
Наиболее
вероятно,
что
центр
рассеивания снарядов находится в1В∂ перед целью.
Для продолжения стрельбы целесообразно увеличить
дальность стрельбы на1В∂.
Отклонение центра рассеивания снарядов по
направлению можно аналогично определить по
соотношению отклонение разрывов снарядов от цели
вправо и влево.
В теории и практике стрельбы очень часто
приходится
решать
задачи,
связанные
с
использованием величины вероятности попадания
снаряда в цель (в некоторую площадь в районе цели).

37.

В этом возникает необходимость, в частности, при
расчете расхода снарядов, необходимого для
поражения различных целей. На вероятность
попадания снаряда в цель влияет рассеивание точек
попадания
снарядов
относительно
центра
рассеивания
положение
центра
рассеивания
снарядов относительно цели. Если рассчитывать
вероятность попадания в цель при заданном
положении
центра
рассеивания,
то
такая
вероятность называется условной.
Рассмотрим наиболее типичные случаи расчета
вероятности попадания снаряда в цель.

38.

Вероятность попадания в прямоугольник со
сторонами, параллельными главным осям
рассеивания. При данной постановке задачи
рассматривается
случай
определения
вероятности попадания снаряда прямоугольник
при условии, что главные оси рассеивания и
стороны
прямоугольника
параллельны
координатным осям, следовательно, когда
система составлена из независимых

39.

У
I
У2
Д
II
У1
Вд
Вб
C
Х
Х1
Х2
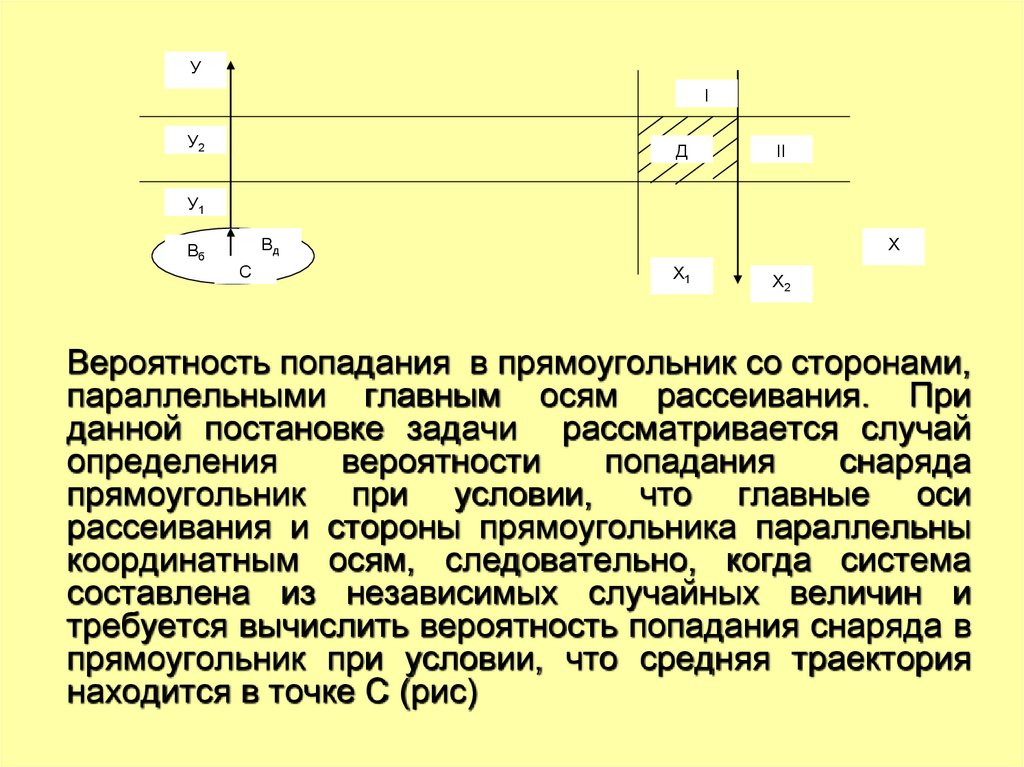
Вероятность попадания в прямоугольник со сторонами,
параллельными главным осям рассеивания. При
данной постановке задачи рассматривается случай
определения
вероятности
попадания
снаряда
прямоугольник при условии, что главные оси
рассеивания и стороны прямоугольника параллельны
координатным осям, следовательно, когда система
составлена из независимых случайных величин и
требуется вычислить вероятность попадания снаряда в
прямоугольник при условии, что средняя траектория
находится в точке С (рис)

40.

Попадание снаряда в прямоугольник Д может
рассматриваться, как сложное событие, состоящие из
одновременного попадания в полосу I и в полосу II. Эти
события
независимые,
поэтому
вероятность
интересующего
нас
события
(попадания
в
прямоугольник Д) найдется по теореме умножения
вероятностей, при этом вероятность попадания в
полосы I и II могут быть найдены по формуле (4).
Вероятность попадания в прямоугольник Д при
заданном положении центра рассеивания снарядов
относительно цели выражается формулой
Р[(Х,У) ЄД] = [F(Х2) - F(Х1)] [F(У2) - F(У1)]
(5)

41.

Вероятность попадания в полосу, расположенную
под углом к главным осям рассеивания. В практике
стрельбы артиллерии весьма частой является
задача по определению вероятности попадания в
полосу (мост, шоссе), расположенную под углом в
плоскости стрельбы.
Эта задача решается достаточно просто, если
известен
закон
ошибок
(закон
рассеивания
снарядов), действующий по интересующему нас
направлению.
Пусть
эллипс
рассеивания
расположен
относительно шоссе так, как изображено на (рис)

42.

α
Вд
d
N
Вб
Х1
Х2
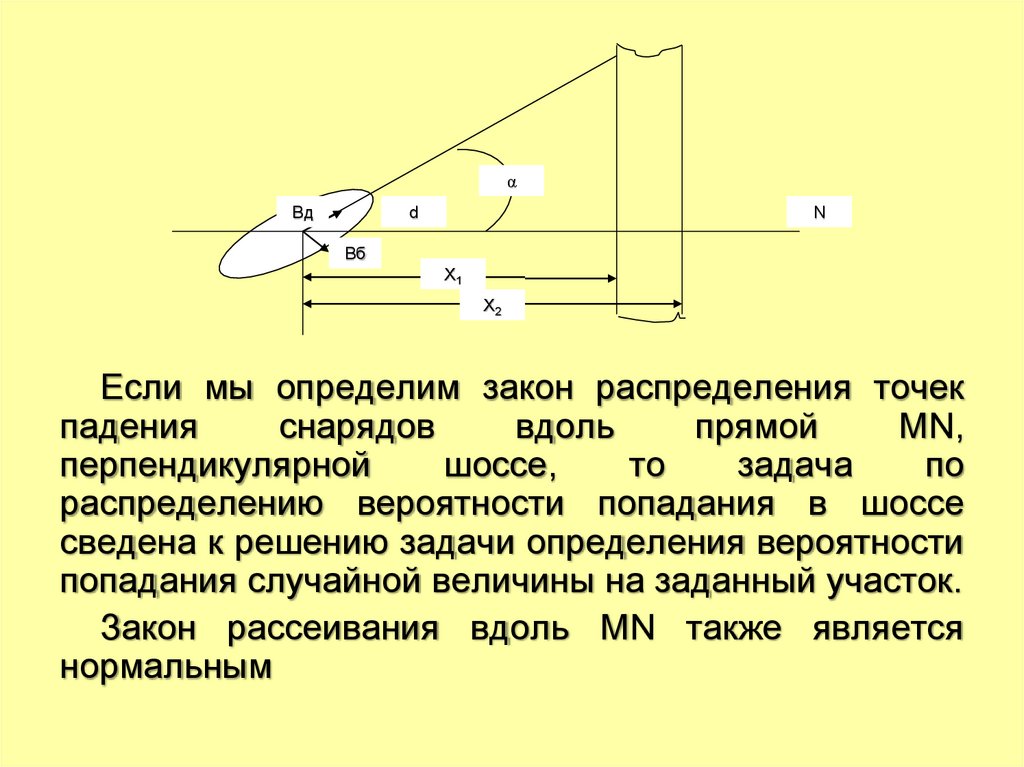
Если мы определим закон распределения точек
падения
снарядов
вдоль
прямой
MN,
перпендикулярной
шоссе,
то
задача
по
распределению вероятности попадания в шоссе
сведена к решению задачи определения вероятности
попадания случайной величины на заданный участок.
Закон рассеивания вдоль MN также является
нормальным

43.

Характеристикой
рассеивания
снарядов
вдоль MN является срединное отклонение
вдоль этой прямой. Величина этого срединного
отклонения определяется по формуле.
d=
2
2
2
В cos α Вб sin α
2
(6)
Вероятность попадания в рассматриваемую
полосу определится по формуле
Р(Х1<Х<Х2) = [Ф(β2)- Ф(β1)]
где β2 =
Х2
d
и β1 =
Х1
d
Ф(β2) и Ф(β1)] - табличные функции

44.

Пример 2.2. По таблицам Ф(β) и с помощью шкалы
рассеивания определить вероятность попадания
снаряда при одном выстреле в полсу минных
заграждений шириной 15м, если центр рассеивания
снарядов находится в 20 м от середины полосы,
направление стрельбы с направлением полосы
составляет угол 60о. В∂ = 20 м, Вб = 8 м.
Р е ш е н и е. Искомую вероятность находят по
формуле
Р(Х1<Х<Х2) = [Ф(β2)- Ф(β1)]
Рассчитывают величину удаления границ полосы
от центра рассеивания
Х2 = 20 + 7,5 = 27,5 м;
Х1 = 20 - 7,5 = 12,5 м;
Рассчитывают величину срединного отклонения
при α = 90 - 60 = 300.
2
2 α Вб 2 sin 2 α 400 3 64 1 316
В
cos
d=
= 17,8 м
4
4

45.

Определяют входы в таблицу значений Ф(β) и
значения этой функции:
β2 = = 1,54; Ф(β2 = 1,54) = 0,70106
β1 = = 0,70; Ф(β1 = 0,70) = 0,36317
Рассчитывают искомую вероятность попадания
снаряда в полосу минных заграждений
Р = (0,70106 - 0,36317) = 0,16894 или Р = 16,9%
По шкале рассеивания (рис.2.23) вероятность
попадания снаряда в полосу β2 = 1,5 В∂ равна 0,25 +
0,09 = 0,34:
в полосу β1 ≈ 0,7 В∂ равна 0,13 + 0,05 = 0,18.
Искомая вероятность попадания снаряда в полосу
минных заграждений будет равна Р = 0,34 =- 0,18 =
0,16 (16%).
Результаты решения практически совпадают.