Вершины, ребра, грани многогранника. Развертка. Многогранные углы. Выпуклые многогранники

1.

Вершины, ребра, грани
многогранника. Развертка.
Многогранные углы. Выпуклые
многогранники . Теорема Эйлера.

2.

3.

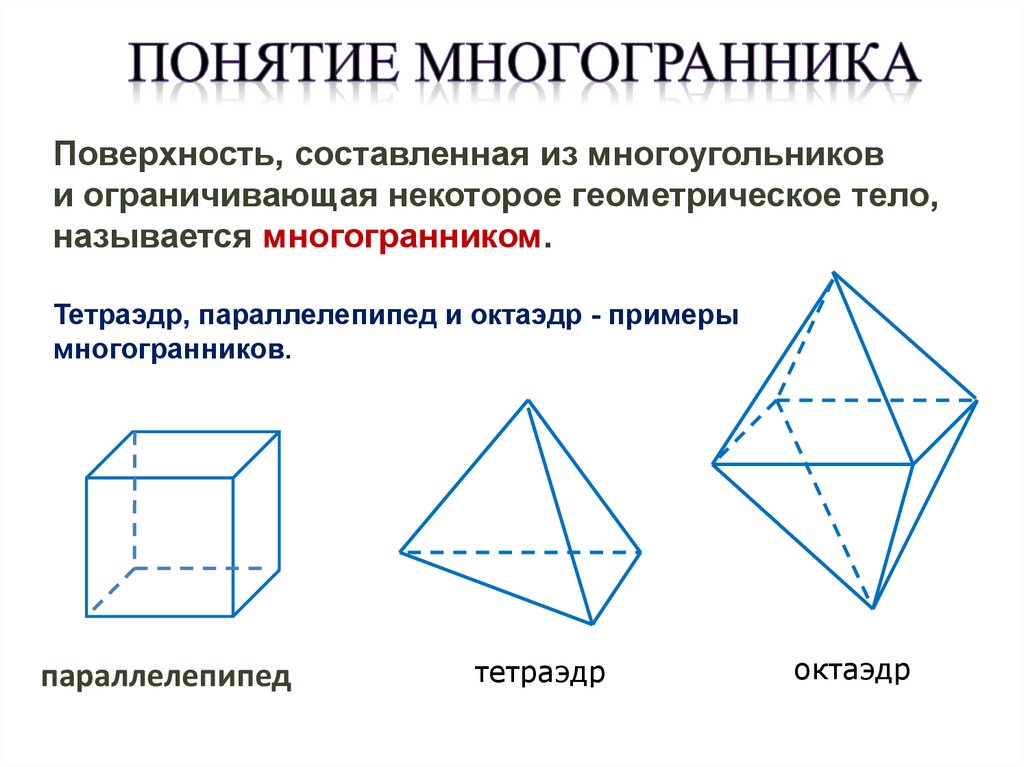
Поверхность, составленная из многоугольников
и ограничивающая некоторое геометрическое тело,
называется многогранником.
Тетраэдр, параллелепипед и октаэдр - примеры
многогранников.
параллелепипед
тетраэдр
октаэдр

4.

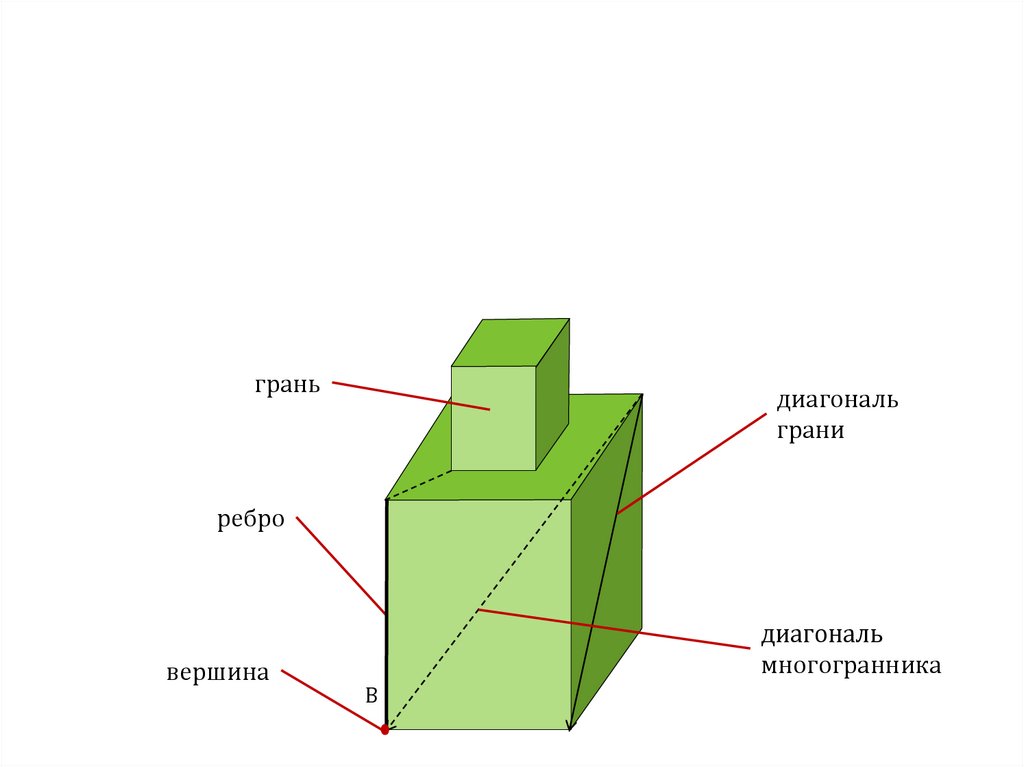
грань
диагональ
грани
ребро
вершина
диагональ
многогранника
B

5.

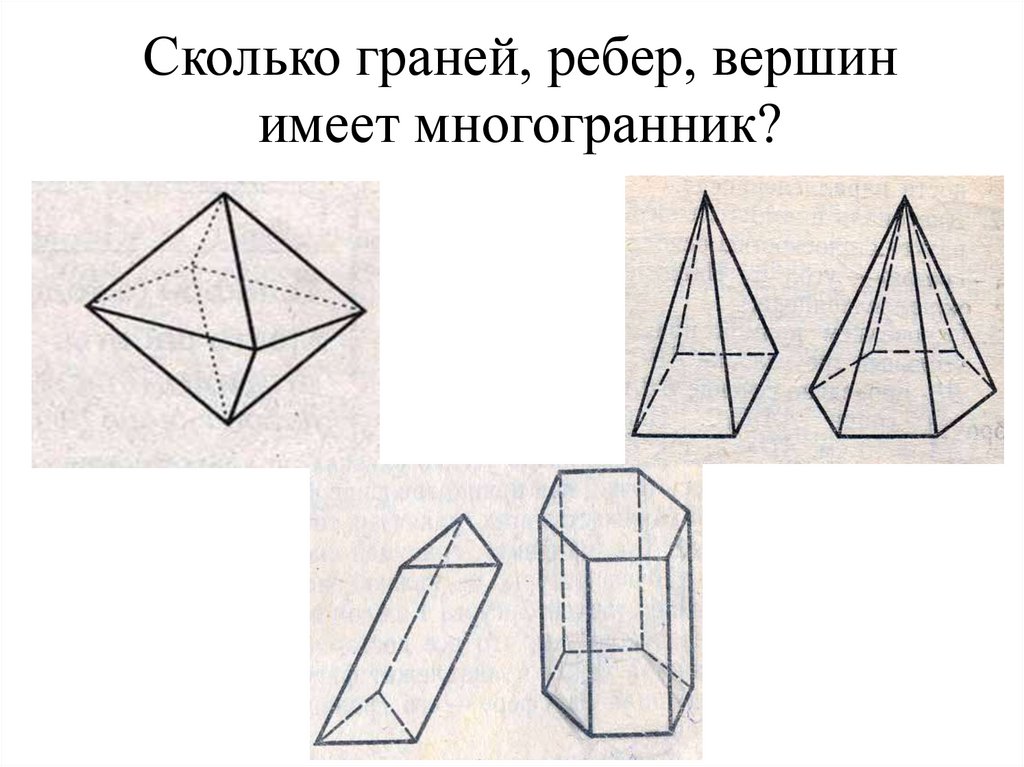
Сколько граней, ребер, вершин
имеет многогранник?

6.

Виды многогранников
Выпуклый многогранник
Многогранник выпуклый, если он
расположен по одну сторону от
плоскости каждой его грани.
Невыпуклый многогранник
Невыпуклый многогранник (плоскостью
поделен на две части)

7.

8.

9.

Теорема Эйлера
Пусть В — число вершин выпуклого многогранника,
Р — число его рёбер
Г — число граней.
Тогда верно равенство:
В 1620 году Рене Декарт показал, что сумма углов всех граней многогранника равна
одновременно 360º (Р — Г) и 360º (В — 2). Из этого непосредственно следует
утверждение теоремы.
В 1750 году Леонард Эйлер доказал тождество для выпуклых многогранников. Теорема
Эйлера заложила фундамент нового раздела математики — топологии. Более строгое
доказательство дал Коши в 1811 г.