Похожие презентации:
Логические величины, основные операции, выражения. Круги Эйлера
1.
Логические величины, основныеоперации, выражения.
Круги Эйлера.
2.
ПонятиеПонятие – форма мышления, фиксирующая
основные существенные признаки объекта.
Понятие имеет:
Содержание – совокупность существенных
признаков объекта.
Объем – совокупность предметов, на которые оно
распространяется.
Пример:
Содержание понятия «Персональный компьютер»
- «Персональный компьютер – это
универсальное электронное устройство для
автоматической обработки информации,
предназначенное для одного пользователя»
Объем понятия «Персональный компьютер»
выражает всю совокупность существующих сейчас
в мире персональных компьютеров.
3.
Объем понятияОбъем понятия может быть представлен в форме
множества объектов, состоящего из элементов
множества.
Алгебра множеств, одна из основополагающих
современных математических теорий, позволяет
исследовать отношения между множествами и,
соответственно, объемами понятий.
4.
Отношения между понятиямиПо отношению друг к другу понятия делятся на
сравнимые и несравнимые.
Далекие друг от друга по своему содержанию
понятия, не имеющие общих признаков,
называются несравнимыми.
Пример:
1) Романс и кирпич.
2) Безответственность и нитка.
Остальные понятия называются сравнимыми.
5.
Отношения между понятиямиДля наглядной геометрической иллюстрации
объемов понятий и соотношений между ними
используются диаграммы Эйлера-Венна.
Если имеются какие-либо понятия A, B, C и т.д., то
объем каждого понятия (множество) можно
представить в виде круга, а отношения между
этими объемами (множествами) в виде
пересекающихся кругов.
Пример:
А ={Натуральные числа (целые положительные числа)}
В ={Четные числа (множество отрицательных и
положительных четных чисел)}
С ={Множество положительных четных чисел}
6.
Отношения между понятиямиСовокупность всех существующих множеств
образует всеобщее универсальное множество 1,
которое позволяет отобразить множество
логически противоположное к заданному. Так,
¬А
если задано множество А, то существует
множество ¬ А, которое объединяет все объекты,
не входящие во множество А. Множество ¬ А
дополняет множество А до универсального
множества U.
U
А
¬А
7.
Виды отношений между понятиямиРавнозначность (тождество)
Перекрещивание (пересечение)
Подчинение (субординация)
Соподчинение
Противоположность
Противоречие
8.
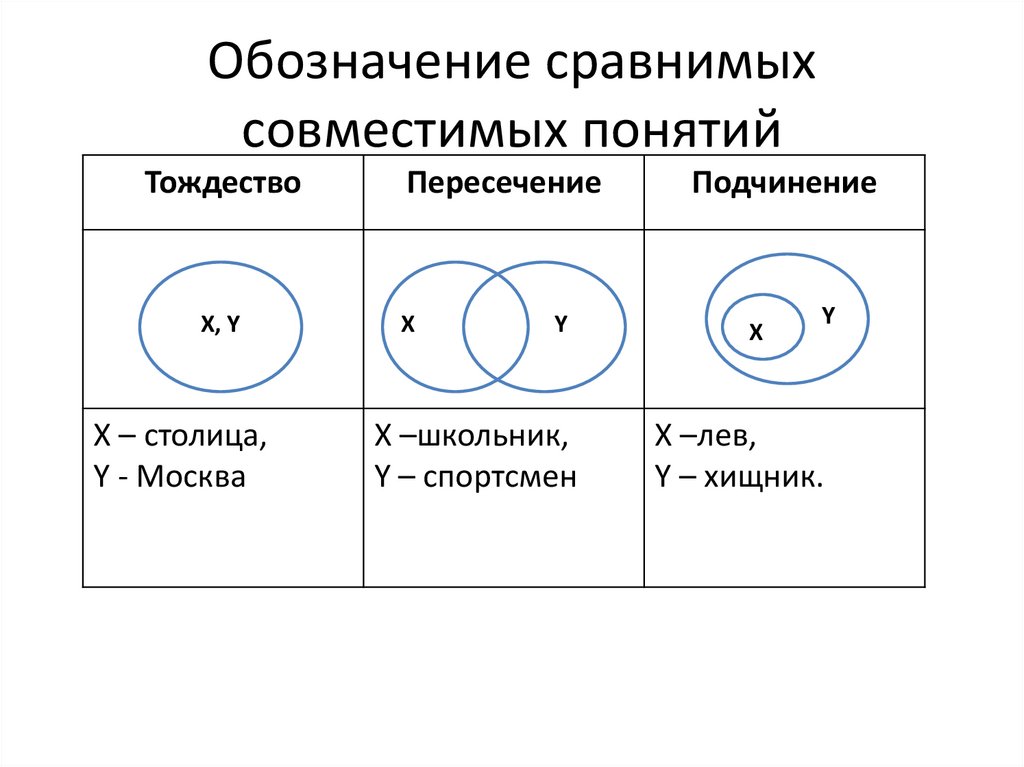
Обозначение сравнимыхсовместимых понятий
Тождество
X, Y
X – столица,
Y - Москва
Пересечение
X
Y
X –школьник,
Y – спортсмен
Подчинение
X
Y
X –лев,
Y – хищник.
9.
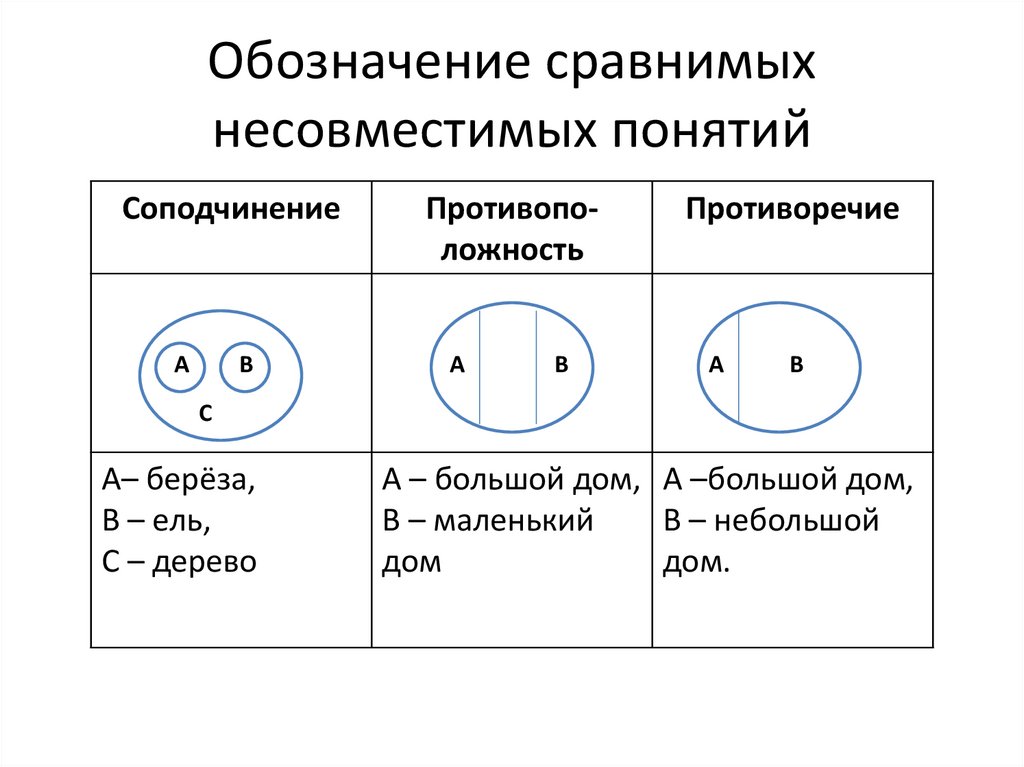
Обозначение сравнимыхнесовместимых понятий
Соподчинение
A
B
Противоположность
A
B
Противоречие
A
B
C
A– берёза,
B – ель,
C – дерево
A – большой дом, A –большой дом,
B – маленький
B – небольшой
дом
дом.







 Математика
Математика








