Использование ИКТ при обучении учащихся исследованию функции по графику производной

1. Использование ИКТ при обучении учащихся исследованию функции по графику производной

Автор: Палто А. В.
учитель математики
МОУ «Волосовская СОШ №1»

2. Проблема:

Как сделать обучение ,
гарантирующим
результат?

3. Цель проекта

Создать наглядный материал
по исследованию функций с
использованием ИКТ

4. Задачи проекта

1.
Выяснить,
в
чем
состоит
геометрический смысл производной
2. Выяснить, как найти промежутки
возрастания и убывания функции, точки
экстремума функции
3. Составить алгоритм действий в каждом
конкретном случае
4. Создать наглядный материал, который
поможет хорошо усвоить тему

5.

6.

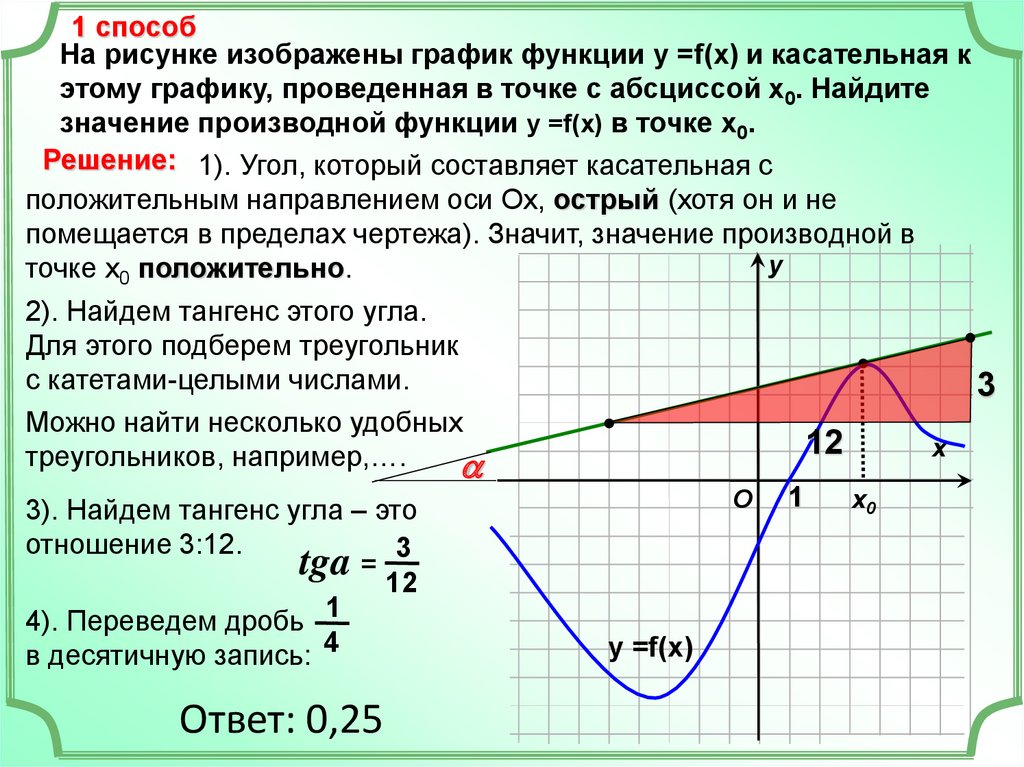
1 способ
На рисунке изображены график функции у =f(x) и касательная к
этому графику, проведенная в точке с абсциссой х0. Найдите
значение производной функции у =f(x) в точке х0.
Решение: 1). Угол, который составляет касательная с
положительным направлением оси Ох, острый (хотя он и не
помещается в пределах чертежа). Значит, значение производной в
у
точке х0 положительно.
2). Найдем тангенс этого угла.
Для этого подберем треугольник
с катетами-целыми числами.
3
Можно найти несколько удобных
12
х
треугольников, например,….
a
O 1
х0
3). Найдем тангенс угла – это
отношение 3:12.
3
tga = 12
4). Переведем дробь 1
в десятичную запись: 4
Ответ: 0,25
у =f(x)

7. Алгоритм 1

• 1. Какой угол между касательной и
положительным направлением оси Ох,
острый или тупой?
• 2. Найти тангенс этого угла. Для этого
нужно подобрать треугольник, катеты
которого целые числа
• 3. Вычислить тангенс угла и дать ответ
в виде десятичной дроби

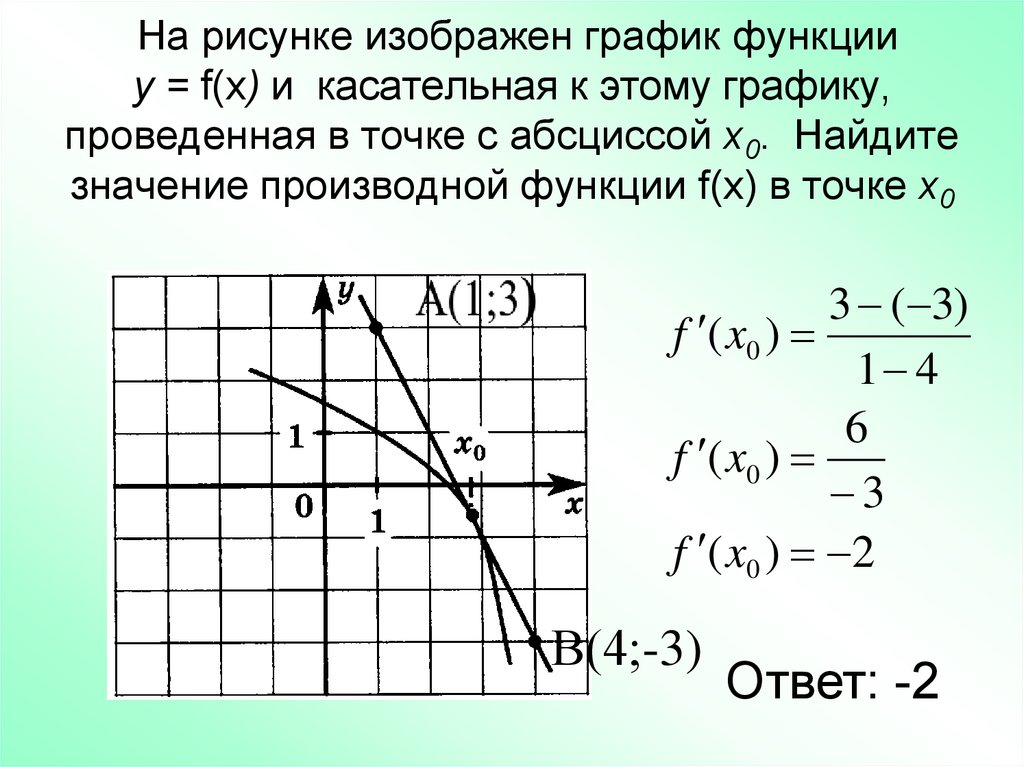
8. На рисунке изображен график функции у = f(x) и касательная к этому графику, проведенная в точке с абсциссой х0. Найдите

значение производной функции f(x) в точке х0
3 ( 3)
f ( x0 )
1 4
6
f ( x0 )
3
f ( x0 ) 2
В(4;-3)
Ответ: -2

9. Алгоритм 2

• Найти координаты точек, выделенных
на координатной плоскости
• Подставить в формулу для нахождений
значения углового коэффициента
касательной координаты точек
• Вычислить значение полученной дроби

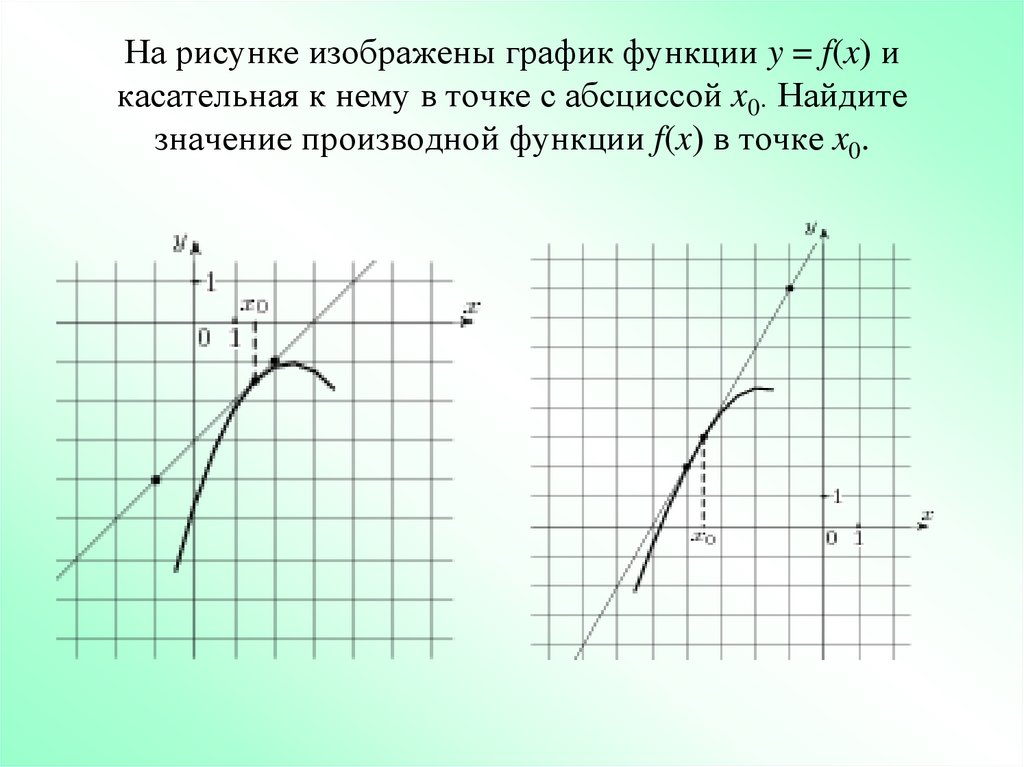
10. На рисунке изображены график функции y = f(x) и касательная к нему в точке с абсциссой x0. Найдите значение производной

На рисунке изображены график функции y = f(x) и
касательная к нему в точке с абсциссой x0. Найдите
значение производной функции f(x) в точке x0.

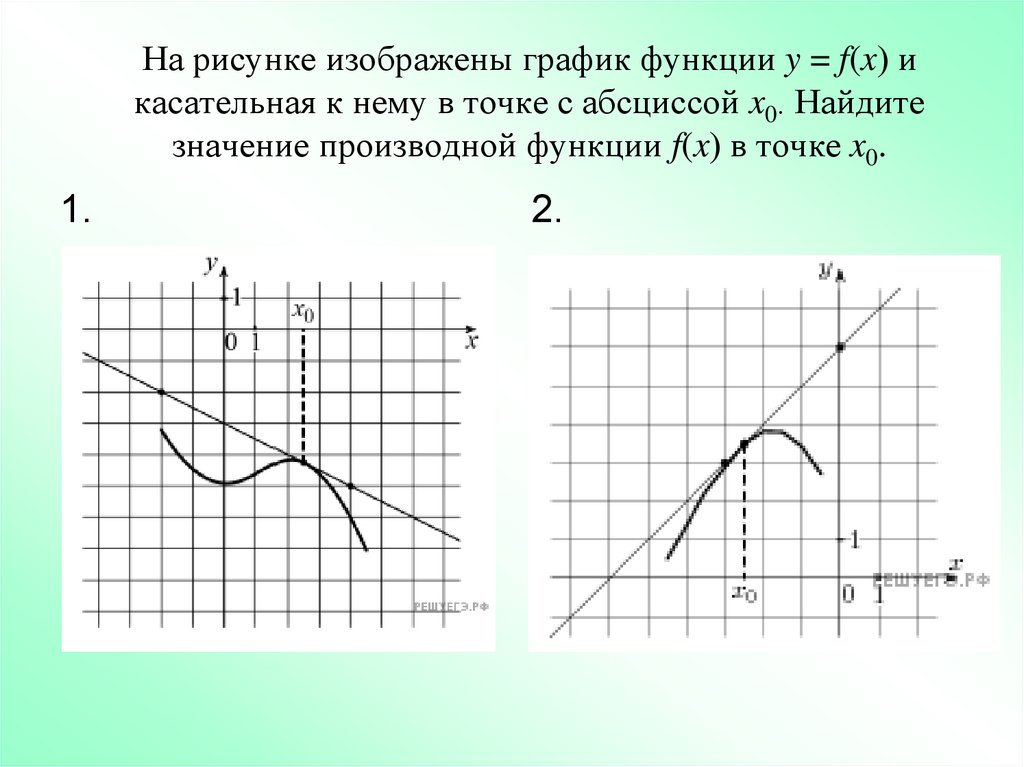
11. На рисунке изображены график функции y = f(x) и касательная к нему в точке с абсциссой x0. Найдите значение производной

На рисунке изображены график функции y = f(x) и
касательная к нему в точке с абсциссой x0. Найдите
значение производной функции f(x) в точке x0.
1.
2.

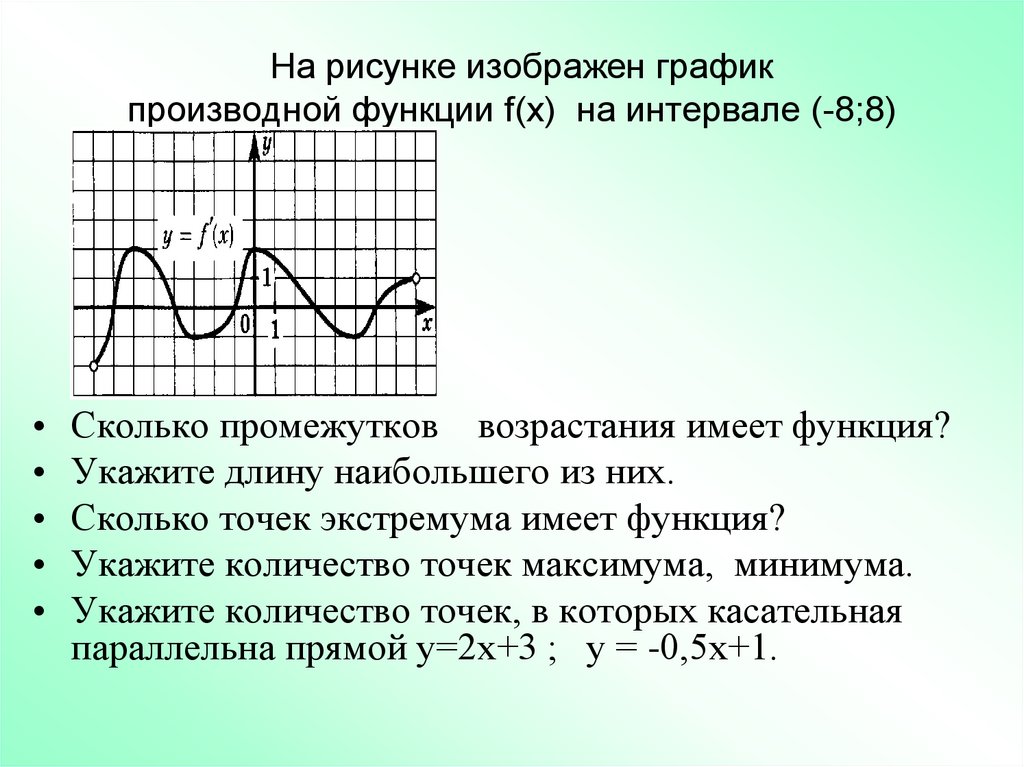
12. На рисунке изображен график производной функции f(x) на интервале (-8;8)

Сколько промежутков возрастания имеет функция?
Укажите длину наибольшего из них.
Сколько точек экстремума имеет функция?
Укажите количество точек максимума, минимума.
Укажите количество точек, в которых касательная
параллельна прямой у=2х+3 ; у = -0,5х+1.

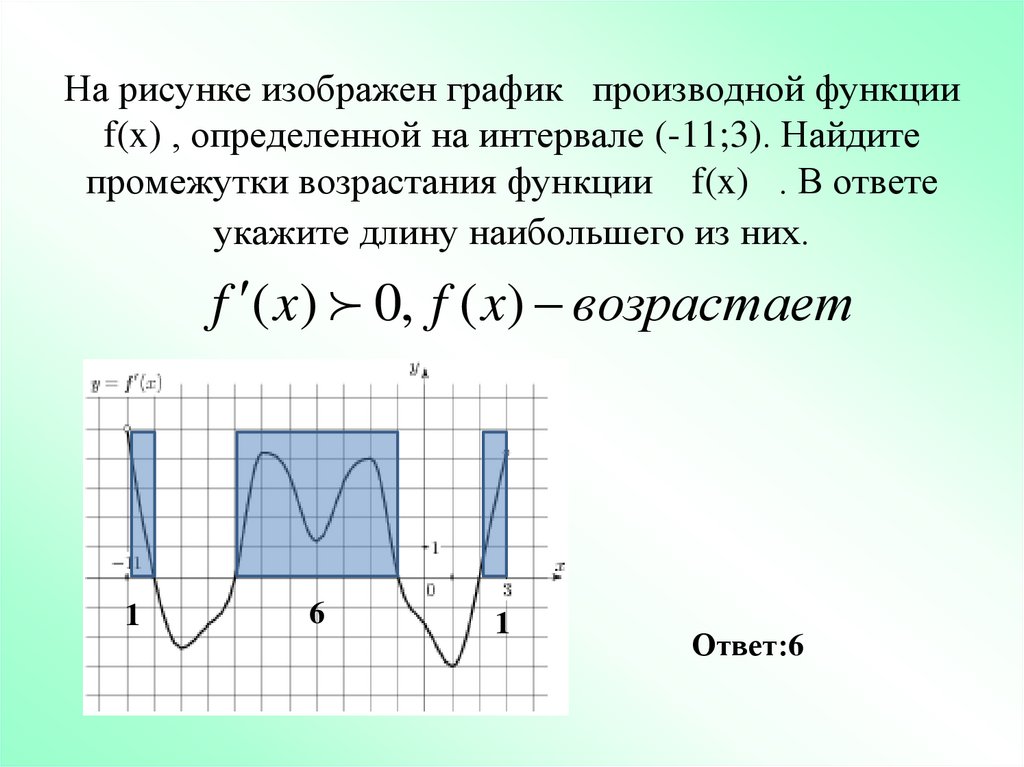
13. На рисунке изображен график   производной функции f(x) , определенной на интервале (-11;3). Найдите промежутки возрастания

На рисунке изображен график производной функции
f(x) , определенной на интервале (-11;3). Найдите
промежутки возрастания функции f(x) . В ответе
укажите длину наибольшего из них.
f ( x) 0, f ( x) возрастает
1
6
1
Ответ:6

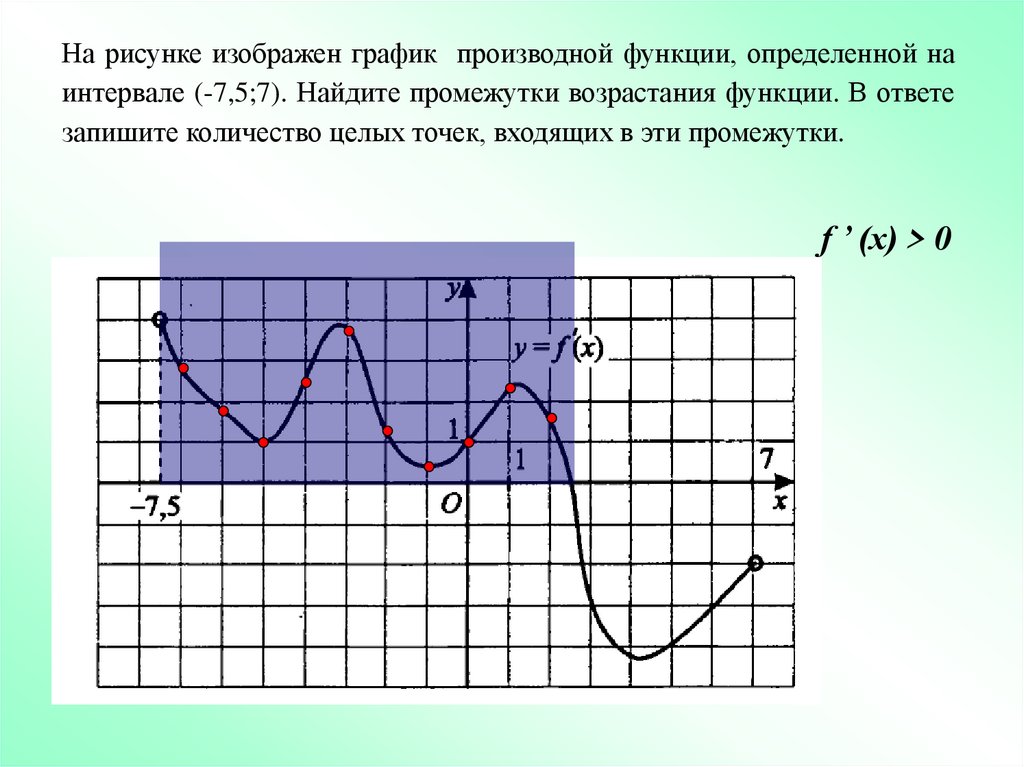
14.

На рисунке изображен график производной функции, определенной на
интервале (-7,5;7). Найдите промежутки возрастания функции. В ответе
запишите количество целых точек, входящих в эти промежутки.
f ’ (x) > 0

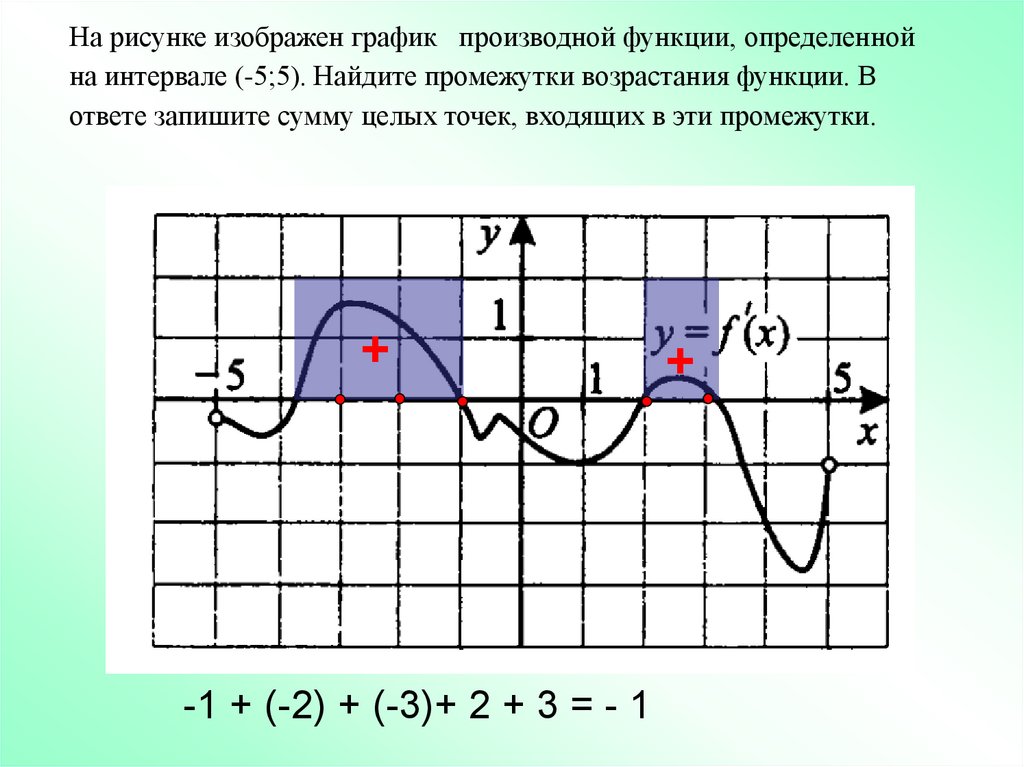
15.

На рисунке изображен график производной функции, определенной
на интервале (-5;5). Найдите промежутки возрастания функции. В
ответе запишите сумму целых точек, входящих в эти промежутки.
+
-1 + (-2) + (-3)+ 2 + 3 = - 1
+

16.

На рисунке изображен график производной функции
,
определенной на интервале (-5;5). Найдите точку максимума функции
на интервале (-3;3)
+
+
–
х=-1

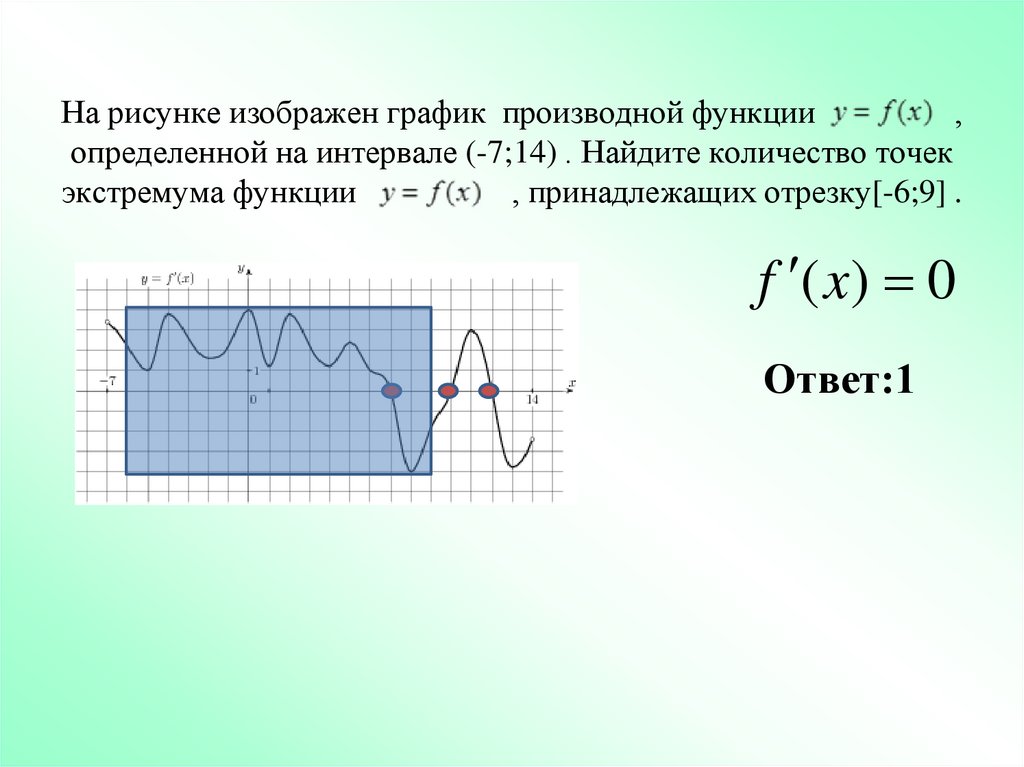
17. На рисунке изображен график  производной функции , определенной на интервале (-7;14) . Найдите количество точек экстремума

На рисунке изображен график производной функции
,
определенной на интервале (-7;14) . Найдите количество точек
экстремума функции
, принадлежащих отрезку[-6;9] .
f ( x) 0
Ответ:1

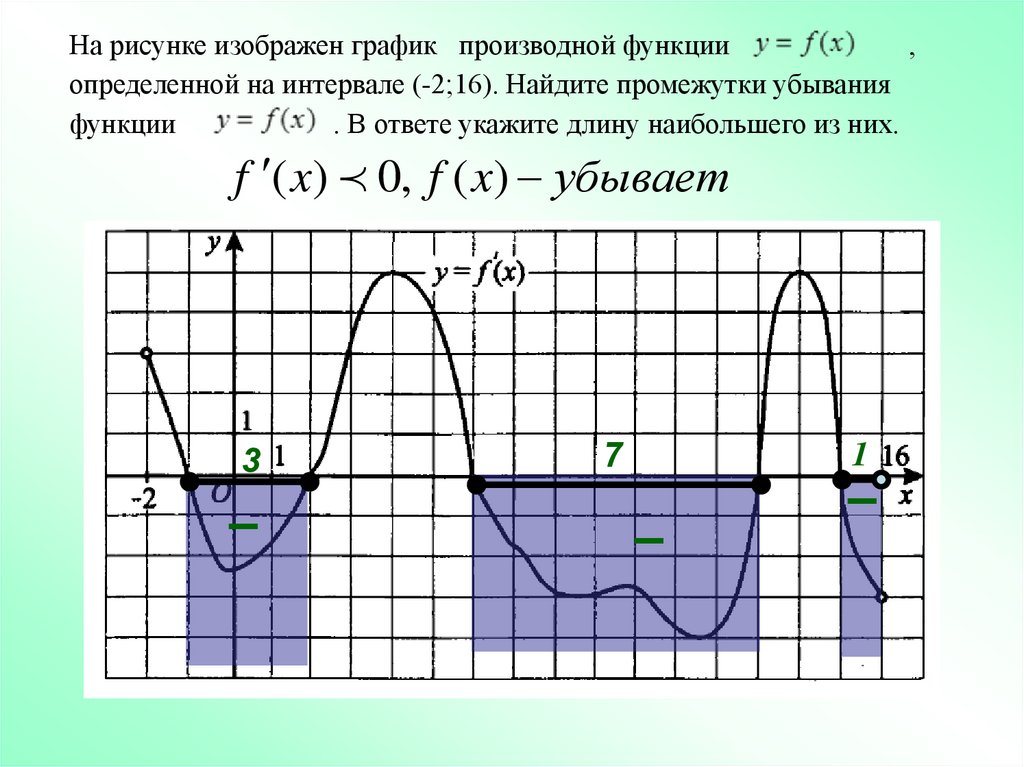
18.

На рисунке изображен график производной функции
,
определенной на интервале (-2;16). Найдите промежутки убывания
функции
. В ответе укажите длину наибольшего из них.
f ( x) 0, f ( x) убывает
3
–
1
7
–
–