Похожие презентации:
Решение квадратных неравенств
1.
Решение квадратныхнеравенств
2.
1. Среди приведенных уравнений укажитеуравнения, задающие квадратичную
функцию:
1) у = 2х2 + х - 1;
2) у2 = х + 1;
3) у2 = х2 - 1;
4) у = -х - х2;
5) у2 = х2;
6) у = -х2.
Для указанных функций назовите
коэффициенты квадратного трехчлена (в
формуле у = ах2 + bх + с).
3.
Определить количество корней уравнения ах2 + вх + с = 0 изнак коэффициента а, если график квадратной функции
у = ах2 + вх + с расположен следующим образом:
4.
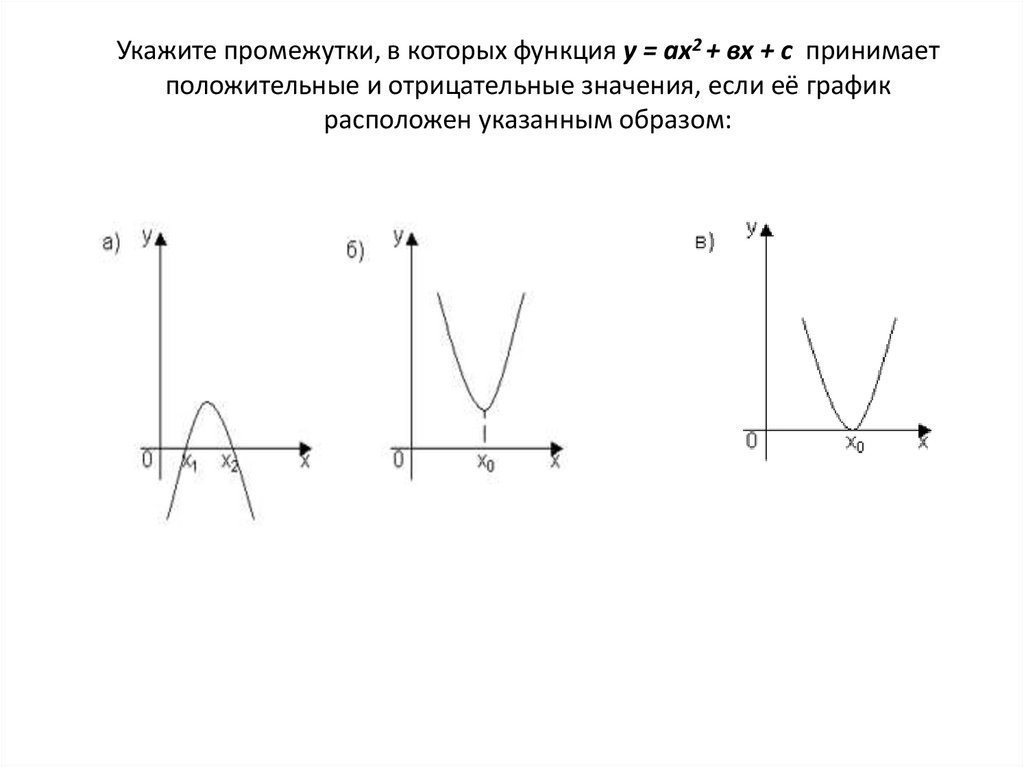
Укажите промежутки, в которых функция у = ах2 + вх + с принимаетположительные и отрицательные значения, если её график
расположен указанным образом:
5.
Найдите нули функции (если они существуют):6.
Определение.Неравенства вида ах2 + bх + с > 0 (< 0; ≥ 0; ≤ 0)
называются квадратными, если а≠ 0.
Пример.
3х2 - 2х - 1 > 0,
x2 - 9 ≥ 0,
х2 - 2х ≤ 0,
х2 > 0
7.
Решить неравенство:5х2 + 9х – 2 > 0.
8.
9.
Алгоритм решения квадратных неравенств :1. Рассмотреть функцию, соответствующую
данному неравенству, определить
направление ветвей параболы.
2. Найти нули функции, т.е. абсциссы точек
пересечения параболы с осью х, если они
есть.
3. Изобразить схематически параболу в
координатной плоскости.
4. Выбрать нужные промежутки.
5. Записать ответ.
10.
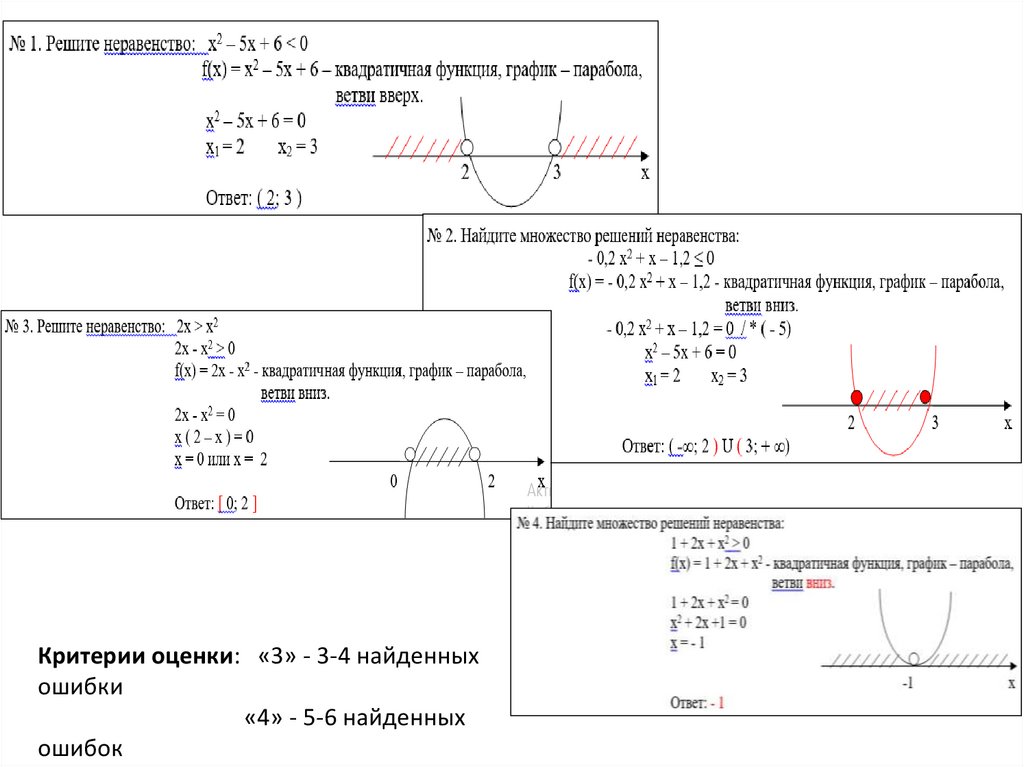
Решение тренировочныхупражнений:
1. Решите неравенство:
х2 – 5х + 6 < 0
2. Найдите множество решений неравенства:
- 0,2 х2 + х – 1,2 ≤ 0
3. Решите неравенство:
2х > х2
4. Найдите множество решений неравенства:
1 + 2х + х2 > 0
11.
Критерии оценки: «3» - 3-4 найденныхошибки
«4» - 5-6 найденных
ошибок
12.
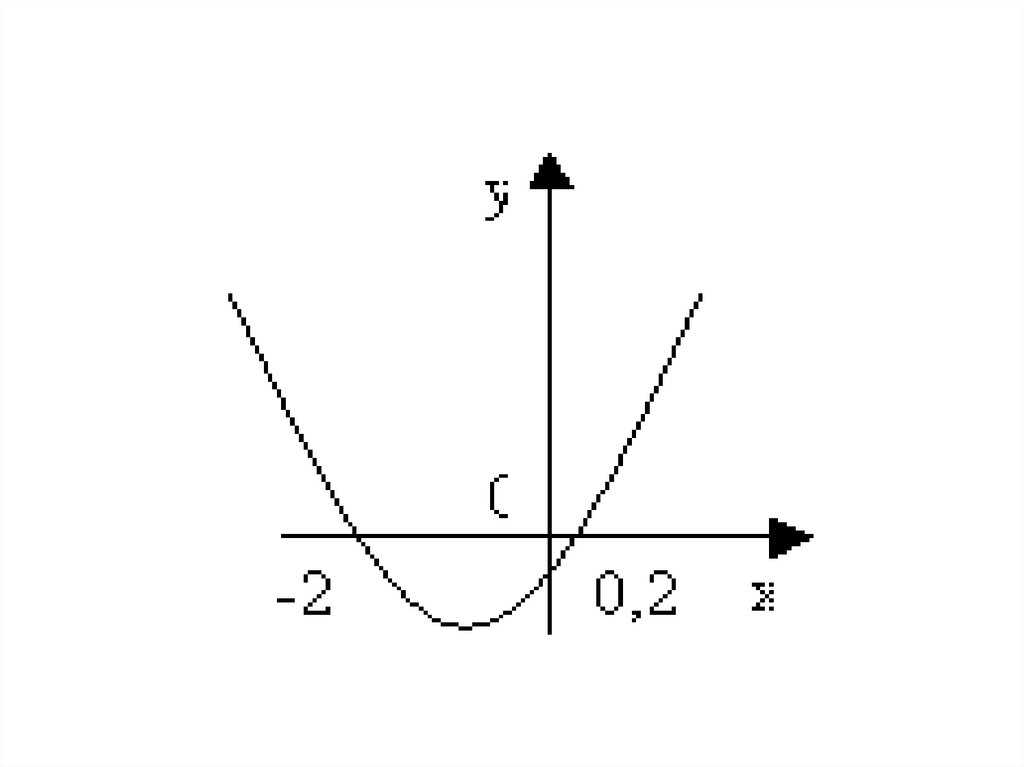
Контрольные вопросы• 1. Определите знак
• коэффициента а,
• коэффициента с,
• дискриминанта D
по графику функции у = ах2 + bх + с, изображенному на
рисунке:
13.
Контрольные вопросы• 2. Какое квадратное неравенство имеет решением
промежуток:
• 1) x ∈ [1; 3];
• 2) x ∈ R;
• 3) х ∈ (-∞; -4) ∪(0; +∞);
• 4) решений нет.
14.
Домашнее задание• П.12 читать, стр113-115
• №404(2,3,4,6), 405(1-5) стр117
15.
Рефлексия– Какова была цель нашего урока?
– Сформулируйте определение квадратного неравенства
– Как решать такие неравенства?
– Алгоритм решения.













 Математика
Математика








