Похожие презентации:
Производная, первообразная
1.
Производная, первообразнаяХомкина Н.Н., учитель математики
МОУ Нижнебузулинская СОШ
Свободненского района Амурской области
2.
«Мечтать – легко и приятно, но думатьтрудно. Умственный труд едва ли не самый
тяжёлый труд для человека».
К.Д.Ушинский
3.
Составьпару
x
5
x
3
2 минуты - работа в парах.
х
1
6
1
x 2 11
a
2х
2
x
7
-3
-sinx
12
8
2 x
4
5x
2
3
13 x
18
5
3x
4
4
9
10
ax
14
0
1
17
2
3
Sinх
cosx
16
1
19
15
12 x
5
20
4.
1. Каков физический смысл производной функции?Мгновенную скорость v(t) движения материальной точки называют
производной функции пути s(t). Производная от функции в данной точке – это
скорость изменения функции.
2. Что является графиком линейной функции?
Графиком линейной функции y= k x + b является прямая.
3. Что называют угловым коэффициентом прямой?
Угловым коэффициентом прямой называют число k = tg α, где α – угол между
прямой y= k x + b и осью ОХ.
Если k>0, то функция y= k x + b возрастает
Если k<0, то функция y= k x + b убывает.
4. Каков геометрический смысл производной функции?
Геометрический смысл производной состоит в том, что значение производной
функции f(x) в точке x˳ равно угловому коэффициенту касательной к графику
функции y=f(x) в точке (x˳; f(x˳)), который в свою очередь равен тангенсу угла
наклона данной касательной к оси абсцисс, т.е. f´(x˳) = tg α
5. Какие промежутки называются промежутками монотонности функции?
Промежутки возрастания и убывания функции называют промежутками
монотонности этой функции.
5.
6.На каких промежутках функция возрастает?Если функция непрерывна на отрезке [a; b], а её производная
положительна на интервале (a; b), f′(x)>0 , то функция возрастает на
отрезке [a; b].
Иначе говоря, положительным значениям производной соответствуют
промежутки, на которых функция возрастает.
7.На каких промежутках функция убывает?
Если функция непрерывна на отрезке [a; b], а её производная
отрицательна на интервале (a; b), f′(x)<0, то функция убывает на
отрезке [a; b], т.е. отрицательным значениям производной
соответствуют промежутки , на которых функция убывает.
8. Какая точка называется точкой максимума?
Точка хо называется точкой максимума функции f(х), если существует
такая окрестность точки хо, что для всех х ≠ хо из этой окрестности
выполняется неравенство f (x) < f (xо).
9. Какая точка называется точкой минимума?
Точка хо называется точкой минимума функции f(x), если существует
такая окрестность точки хо, что для всех х ≠ хо из этой окрестности
выполняется неравенство f (x) > f (xо).
6.
10. Какие точки называются точками экстремума?Точки минимума и точки максимума называются точками
экстремума.
Если производная в некоторой точке равна нулю, а в ее
окрестности меняет знак, то это точка экстремума, то есть
точки экстремума соответствуют точкам смены знака
производной.
11. Когда точка хо является точкой максимума?
Если производная при переходе через точку хо, меняет знак
с плюса на минус, то хо- точка максимума.
12. Когда точка хо является точкой минимума?
Если производная при переходе через точку хо, меняет знак
с минуса на плюс, то хо- точка минимума.
13. Необходимое условие экстремума?
Если хо- точка экстремума дифференцируемой функции, то
f′( хо)=0.
7.
Задача.Материальная точка движется прямолинейно по
закону x (t) = 6t2 – 48 t + 17 (где x — расстояние от
точки отсчета в метрах, t — время в секундах,
измеренное с начала движения). Найдите ее
скорость (в м/с) в момент времени t = 9 с.
Решение.
Найдем закон изменения скорости: v(t) = x ' (t) =
= 12t – 48
При t = 9 c имеем: v(9) = 12 · 9 - 48 = 60 (м/с).
Ответ: 60.
8.
1. Материальная точка движется прямолинейно позакону x(t) = - t 4 + 6t3 + 5t + 23 (где x —
расстояние от точки отсчета в метрах, t —
время в секундах, измеренное с начала
движения). Найдите ее скорость в (м/с) в
момент времени t = 3 с.
Ответ: 59
9.
2.Материальная точка M начинает движение из точки A и
движется по прямой на протяжении 12 секунд. График
показывает, как менялось расстояние от точки A до
точки M со временем. На оси абсцисс откладывается
время t в секундах, на оси ординат — расстояние s.
Определите, сколько раз за время движения скорость
точки M обращалась в ноль (начало и конец движения не
учитывайте).
Ответ: 6
10.
На рисунке изображен графикфункции y = f(x), определенной
на интервале (−6; 5). Найдите
количество точек, в которых
касательная к графику функции
параллельна прямой y = −6.
На рисунке изображен график
производной функции f(x),
определенной на интервале (−10; 2).
Найдите количество точек, в которых
касательная к графику
функции f(x) параллельна
прямой y = −2x − 11 или совпадает с
ней.
Ответ: 7
Ответ: 5
11.
1. На рисунке изображен график функции y = f(x),определенной на интервале (−5; 5). Найдите
количество точек, в которых касательная к
графику функции параллельна прямой y = 6 или
совпадает с ней.
Ответ: 4
12.
2. На рисунке изображен график производнойфункции f(x). Найдите абсциссу точки, в которой
касательная к графику y = f (x ) параллельна
прямой y = 2x - 2 или совпадает с ней.
Ответ: 5
13.
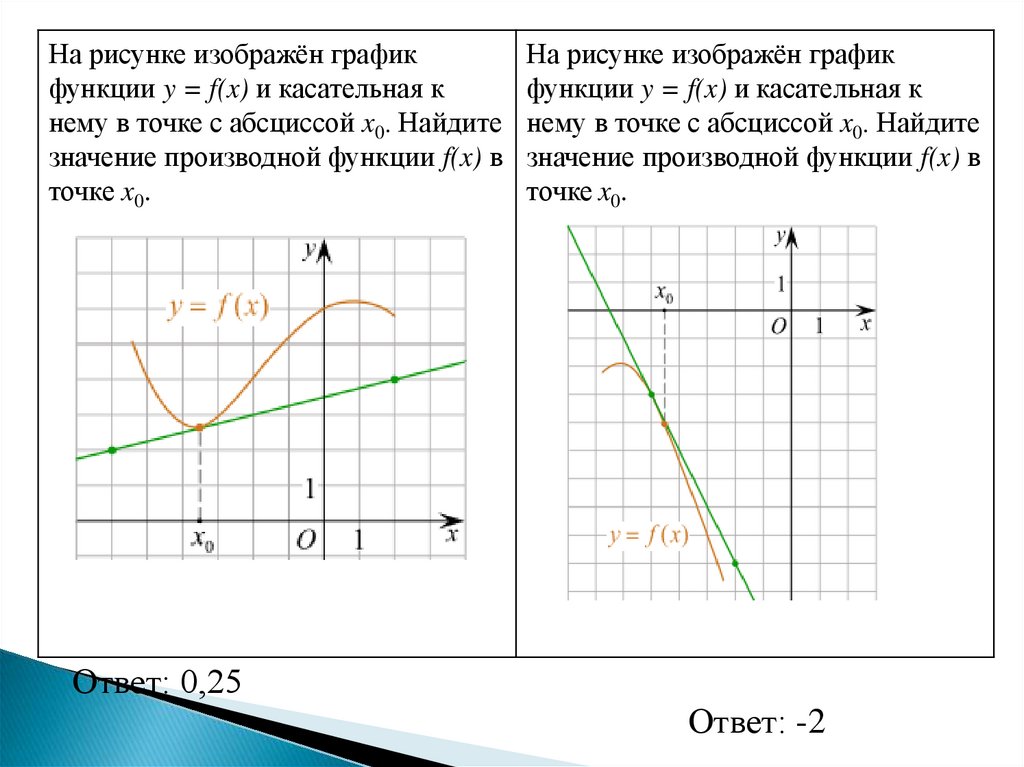
На рисунке изображён графикфункции y = f(x) и касательная к
нему в точке с абсциссой x0. Найдите
значение производной функции f(x) в
точке x0.
На рисунке изображён график
функции y = f(x) и касательная к
нему в точке с абсциссой x0. Найдите
значение производной функции f(x) в
точке x0.
Ответ: 0,25
Ответ: -2
14.
1. На рисунке изображёнграфик функции y =f(x) и
касательная к нему в точке с
абсциссой x0. Найдите
значение производной
функции f(x) в точке x0.
2. На рисунке изображены
график функции y = f(x) и
касательная к нему в точке с
абсциссой x0. Найдите
значение производной
функции f(x) в точке x0.
Ответ: -0, 25
Ответ: 0,25
15.
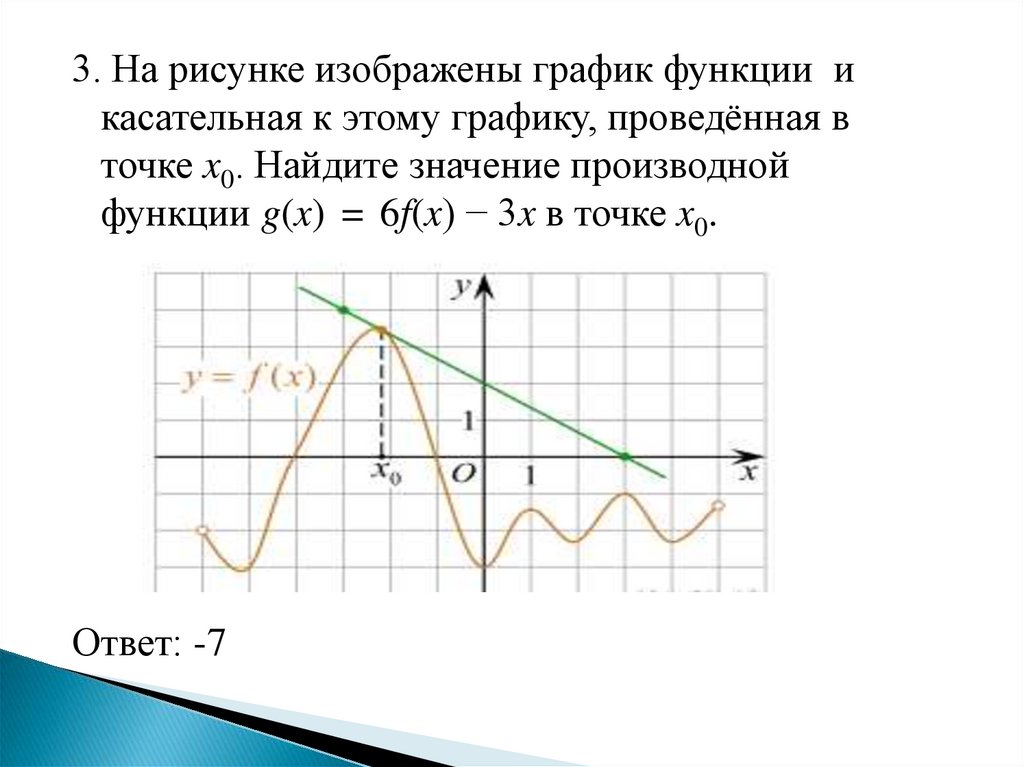
3. На рисунке изображены график функции икасательная к этому графику, проведённая в
точке x0. Найдите значение производной
функции g(x) = 6f(x) − 3x в точке x0.
Ответ: -7
16.
1. На рисунке изображен графикфункции y = f(x), определенной
на интервале (−6; 8).
Определите количество целых
точек, в которых производная
функции положительна.
2. На рисунке изображен
график производной функции
f (x), определенной на интервале
(-6; 6). Найдите промежутки
возрастания функции f (x). В
ответе укажите сумму целых
точек, входящих в эти
промежутки.
Ответ: 4
Ответ: 14
17.
1. На рисунке изображен график функции y = f(x),определенной на интервале (−2; 12). Найдите
сумму точек экстремума функции f(x).
Ответ: 44 (1+2+4+7+9+10+11)
18.
2. На рисунке изображен график производнойфункции f(x), определенной на интервале (−7; 14).
Найдите количество точек максимума
функции f(x) на отрезке [−6; 9].
Ответ: 1
19.
3. На рисунке изображен график производнойфункции f(x), определенной на интервале (−2; 12).
Найдите промежутки убывания функции f(x). В
ответе укажите длину наибольшего из них.
Ответ: 6
20.
4. На рисунке изображён график производнойфункции f (x). На оси абсцисс отмечены восемь
точек: x1, x2, x3, ..., x8. Сколько из этих точек лежит
на промежутках возрастания функции f(x)?
Ответ: 3
21.
ПервообразнаяF(x) – первообразная для функции f(x) на
некотором промежутке, если
F’ (x) = f(x) для любого х из этого промежутка
22.
Задача.На рисунке изображён график функции y = F(x) —
одной из первообразных функции f(x), определённой
на интервале (−3; 5). Найдите количество решений
уравнения f (x) = 0 на отрезке [−2; 4].
Ответ: 10
23.
Задача.На рисунке изображён график некоторой
функции f(x) (два луча с общей начальной точкой).
Пользуясь рисунком, вычислите F(8) − F(2),
где F(x) — одна из первообразных функции f(x).
Ответ: 7
24.
https://mathb-ege.sdamgia.ru/https://www.mathm.ru/zad/ege/zad7eget.html
https://fipi.ru/























 Математика
Математика








