Похожие презентации:
Применение производной при решении задач курса физики, химии, геометрии. Лекция № 6
1.
Лекция №6Применение производной
при решении задач курса
физики, химии,
геометрии.
2.
содержание3.
Физический смысл производной. Пусть материальная точка движетсяпрямолинейно по закону
Тогда средняя скорость точки в промежутке в
времени вычисляется по
формуле
Как известно, мгновенной скоростью v(to) в момент времени to называется
предел (если он существует), к которому стремится средняя скорость за
промежуток времени от
т. е.
Таким образом, мгновенная скорость прямолинейного движения материальной
точки в любой момент-времени t есть производная от пути s по времени i:
В этом заключается физический смысл производной.
Пример: Найти скорость движения точки в момент времени t = 5; если закон
движения задан формулой
Решение. Находим:
Механический смысл второй производной
Пусть материальная точка движется прямолинейно по закону
Тогда, как было показано , скорость движения в момент времени t определяется
по формуле
Если движение неравномерное, то скорость v(t) также есть функция от времени
t. Поэтому производная определяет скорость изменения скорости
материальной точки, движущейся по закону
4.
Но, как известно из механики, скорость изменения скорости называется ускорением, иобозначается a(t). Таким образом, ускорение a{t) прямолинейного движения
материальной точки в момент времени t равно первой производной от скорости по'
времени или второй производной от пути по времени, т. е.
Пример. Тело движется прямолинейно по закону
Найти скорость и ускорение в момент времени t = 3.
Решение. Находим
Задачи прикладного характера
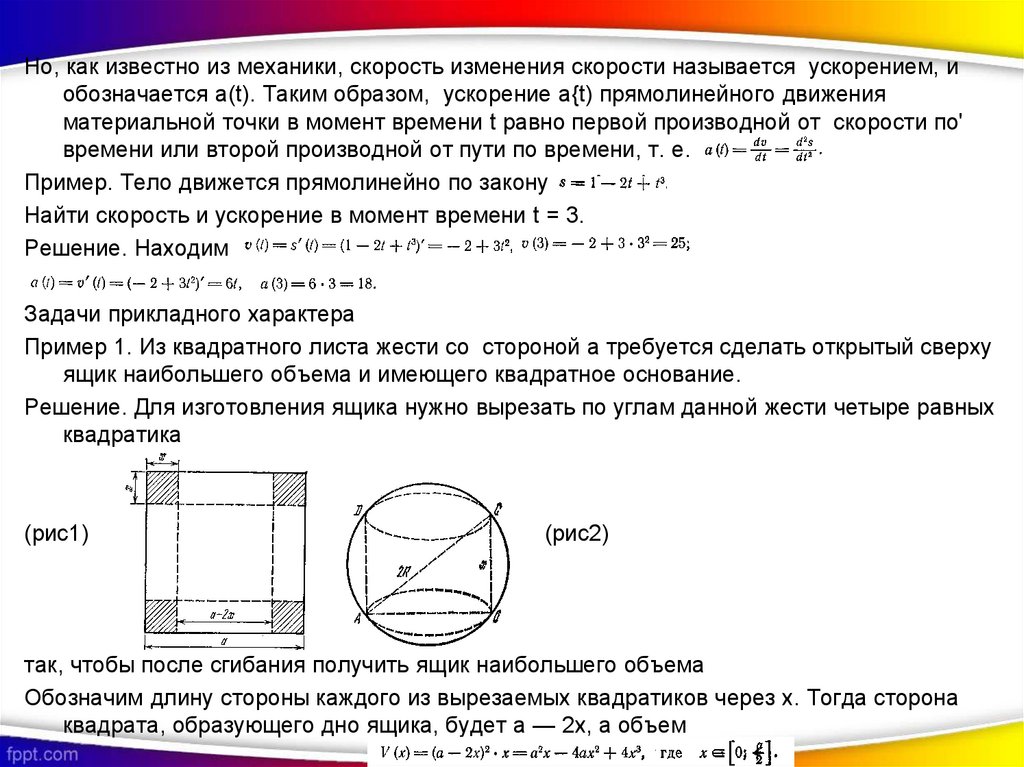
Пример 1. Из квадратного листа жести со стороной а требуется сделать открытый сверху
ящик наибольшего объема и имеющего квадратное основание.
Решение. Для изготовления ящика нужно вырезать по углам данной жести четыре равных
квадратика
(рис1)
(рис2)
так, чтобы после сгибания получить ящик наибольшего объема
Обозначим длину стороны каждого из вырезаемых квадратиков через х. Тогда сторона
квадрата, образующего дно ящика, будет а — 2х, а объем
5.
Найдем наибольшее значение функции V(x) на отрезке. Находим критические точки
первого рода функции V(x):
откуда
Находим значения функции V (х) в точках
Таким образом, ящик будет иметь наибольший объем, если сторона вырезаемого
квадрата равна
Пример 2. Из шара радиуса R выточить цилиндр наибольшего объема.
Решение. Обозначим длину высоты цилиндра через х. Тогда, как видно из рис. 2, радиус
основания цилиндра равен
а объем цилиндра
где
Таким образом, требуется найти наибольшее значение функции V(x) на отрезке [0;2R].
Находим критические точки первого рода функции V(x):
Находим значения функции V (х) в точках
Итак, искомый цилиндр имеет высоту, равную
Задачи для закрепления материала:
1. Найти скорость тела, движущегося по закону
2. Тело движется прямолинейно по закону
t1=0; t2=2 и t3=5
3. Найти скорость движения тела в момент времени
формулой:
Найти скорость тела в моменты
если закон движения задан
6.
4. Когда скорость точки, движущейся прямолинейно по законуравна нулю?
5. Найти ускорение точки в указанные моменты времени t, если скорость точки,
движущейся прямолинейно, определяется законом:
6. Найти скорость и ускорение точки в указанные моменты времени t, движущейся
прямолинейно по закону:
7. Найти момент времени t в который ускорение точки, движущейся прямолинейно по
закону
равно нулю. Какова при этом скорость точки?
8. Тело массы т движется по закону
Доказать, что сила, действующая на
точку, постоянна.
9. Разбить число 5 на два слагаемых, сумма кубов которых
будет наименьшей.
10. В равнобедренный треугольник вписать пряхмоугольник
наибольшей площади.
11. Из листа картона 80 см X 50 см требуется изготовить
открытый сверху ящик наибольшей вместимости, вырезая по углам
равные квадратики и загибая затем получившиеся выступы.
12. Сумма основания и высоты треугольника равна 12 см.
Каковы должны быть размеры основания, чтобы площадь
треугольника была наибольшей?
7.
13. Из всех цилиндров данного объема V найти тот, у которого полная поверхностьнаименьшая.
14. Точка движется прямолинейно по закону
Найти максимальную скорость движения точки.
15. Тело, брошенное вертикально вверх, движется прямолинейно по закону
Найти наибольшую высоту подъема
тела.
.






 Математика
Математика