Элементы алгебры логики

1.

ЭЛЕМЕНТЫ
АЛГЕБРЫ ЛОГИКИ
МАТЕМАТИЧЕСКИЕ ОСНОВЫ
ИНФОРМАТИКИ
Для 8 класса
Составитель
Жаркова С.В.

2.

Алгебра логики (алгебра высказываний) — раздел математической
логики, в котором изучаются логические операции над высказываниями[1].
Чаще всего предполагается, что высказывания могут быть только
истинными или ложными, то есть используется
так называемая бинарная или двоичная логика, в отличие от,
например, троичной логики.
Основоположником её является Дж. Буль, английский математик и логик,
положивший в основу своего логического учения аналогию между алгеброй
и логикой. Алгебра логики стала первой системой математической логики, в
которой алгебраическая символика стала применяться к логическим
выводам в операциях с понятиями, рассматриваемыми со стороны их
объёмов. Буль ставил перед собой задачу решить логические задачи с
помощью методов, применяемых в алгебре. Любое суждение он пытался
выразить в виде уравнений с символами, в которых действуют логические
законы, подобные законам алгебры.

3.

Логика
Аристотель (384-322 до н.э.).
Основоположник формальной логики (понятие,
суждение, умозаключение).
Джордж Буль (1815-1864). Создал новую
область науки - Математическую логику
(Булеву алгебру или Алгебру высказываний).
Клод Шеннон (1916-2001). Его
исследования позволили применить алгебру
логики в вычислительной технике

4.

Высказывание
Выска́зывание в математической логике — предложение,
выражающее суждение. Если суждение, составляющее содержание (смысл)
некоторого высказывания, истинно, то и о данном высказывании говорят, что
оно истинно. Сходным образом ложным называют такое высказывание,
которое является выражением ложного суждения. Истинность и ложность
называются логическими, или истинностными, значениями высказываний[1].
В
русском
языке
высказывания
выражаются
повествовательными предложениями:
Земля вращается вокруг Солнца.
Москва - столица.
Но не всякое повествовательное предложение является
высказыванием:
Это высказывание ложное.
Побудительные и вопросительные предложения
высказываниями не являются.
Без стука не входить!
Откройте учебники.

5.

Алгебра логики
Алгебра
логики
вычисления значений,
высказываний.
определяет
упрощения
правила
записи,
и преобразования
В алгебре логики высказывания обозначают буквами и
называют логическими переменными.
Если
высказывание
истинно,
то
значение
соответствующей ему логической переменной обозначают
единицей (А = 1), а если ложно - нулём (В = 0).
0 и 1 называются логическими значениями.

6.

Простые и сложные
высказывания
Высказывания бывают простые и сложные.
Высказывание называется простым, если никакая его
часть сама не является высказыванием.
Сложные (составные) высказывания строятся из простых с
помощью логических операций.
Название логической операции
Логическая связка
Конъюнкция
«и»; «а»; «но»; «хотя»
Дизъюнкция
«или»
Инверсия
«не»; «неверно, что»

7.

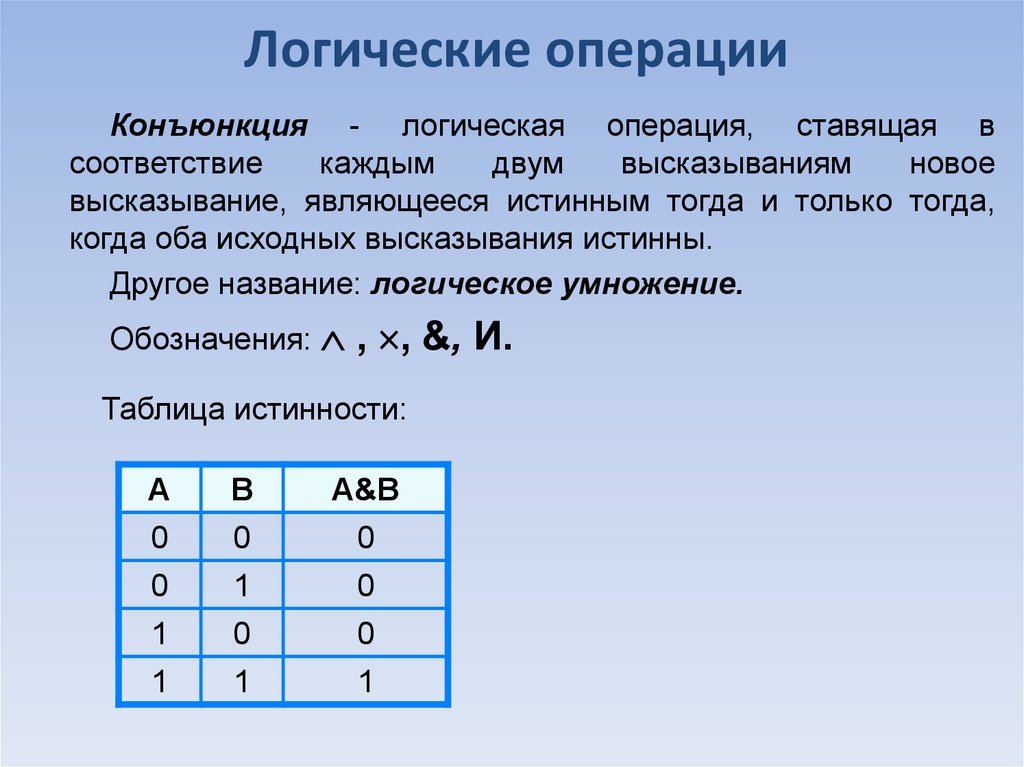
Логические операции
Конъюнкция - логическая операция, ставящая в
соответствие
каждым
двум
высказываниям
новое
высказывание, являющееся истинным тогда и только тогда,
когда оба исходных высказывания истинны.
Другое название: логическое умножение.
Обозначения:
, , &, И.
Таблица истинности:
А
В
А&В
0
0
0
0
1
0
1
0
0
1
1
1

8.

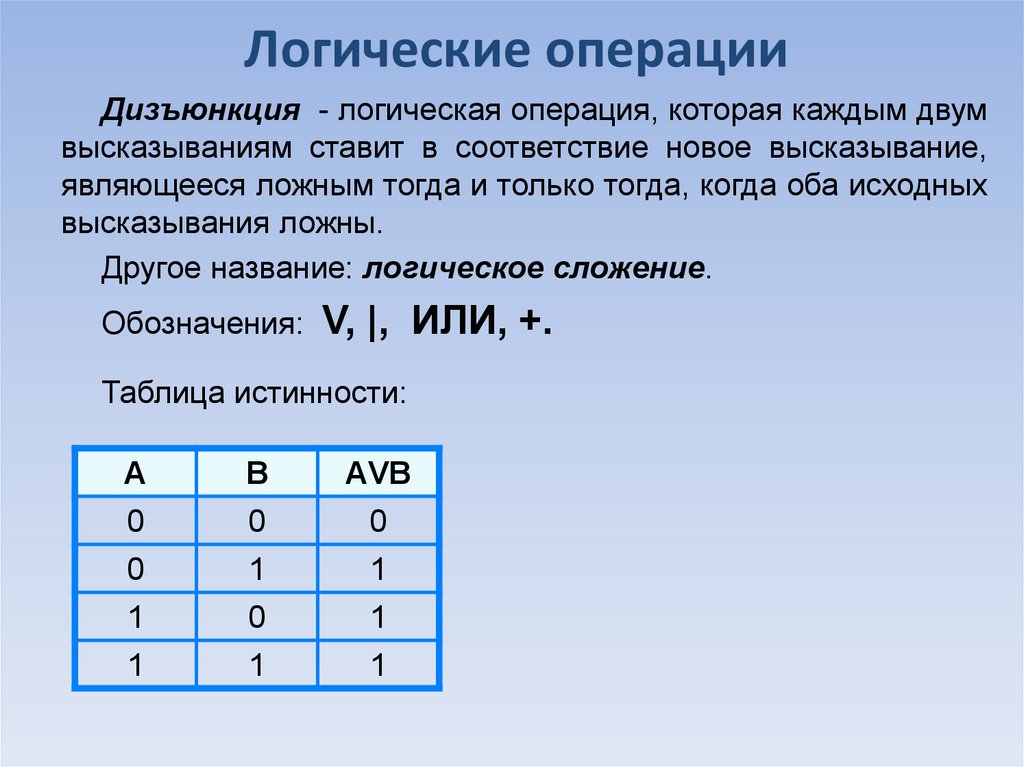
Логические операции
Дизъюнкция - логическая операция, которая каждым двум
высказываниям ставит в соответствие новое высказывание,
являющееся ложным тогда и только тогда, когда оба исходных
высказывания ложны.
Другое название: логическое сложение.
Обозначения:
V, |, ИЛИ, +.
Таблица истинности:
А
В
АVВ
0
0
0
0
1
1
1
0
1
1
1
1

9.

Логические операции
Инверсия - логическая операция, которая каждому
высказыванию ставит в соответствие новое высказывание,
значение которого противоположно исходному.
Другое название: логическое отрицание.
Обозначения: НЕ,
¬,¯
Таблица истинности:
А
Ā
0
1
1
0
.

10.

Пример построения таблицы истинности
АVA&B
n = 2, m = 22 = 4.
Приоритет операций: &, V
A
B
A&B
AVA&B
0
0
0
0
0
1
0
0
1
0
0
1
1
1
1
1

11.

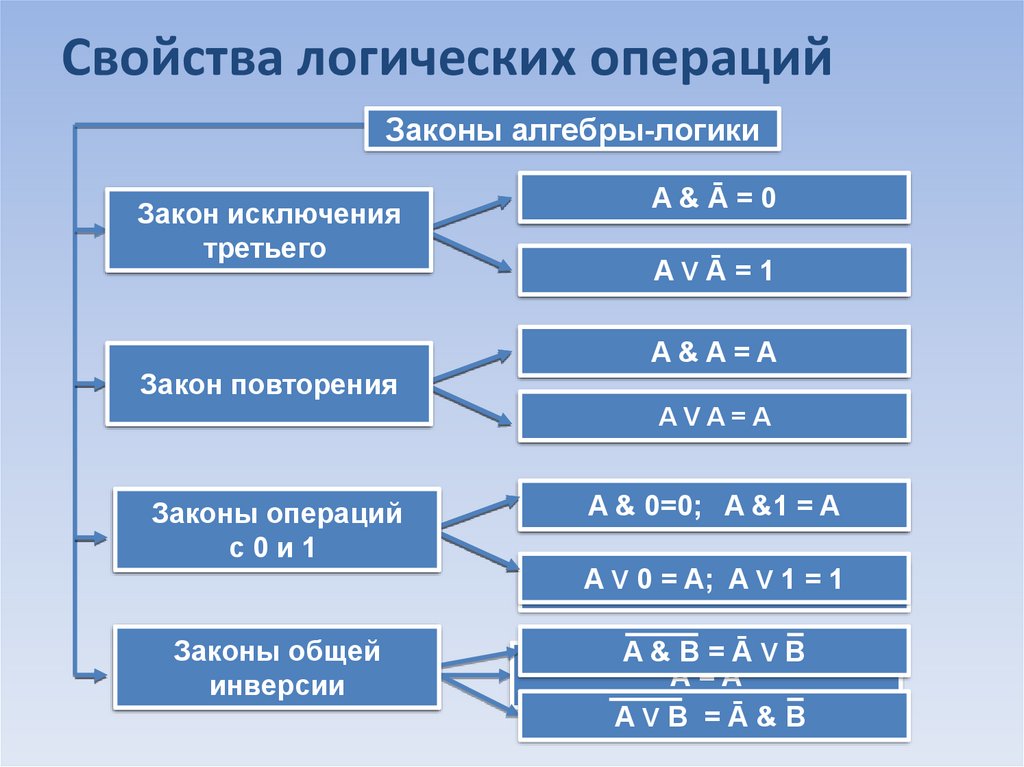
Свойства логических операций
Законы алгебры-логики
Закон исключения
Переместительный
третьего
A&
AB
&=
ĀB
=&
0A
AV
AB
VĀ
=B
=V
1A
(A & B) &
AC
& =AA= &
A ( B & C)
Закон
Сочетательный
повторения
(A V B) V
AC
VA
=A=VA( B V C)
Законы операций
Распределительный
с0и1
A&(B
A&
VC)=
0=0;(A&B)
A &1V =(A&C)
A
V 0 ==A;(AA
V1=1
AVA
(B&C)
VB)&(A
VC)
Закон
Законы
двойного
общей
отрицания
инверсии
A&B=ĀVB
Ā=A
AVB =Ā&B

12.

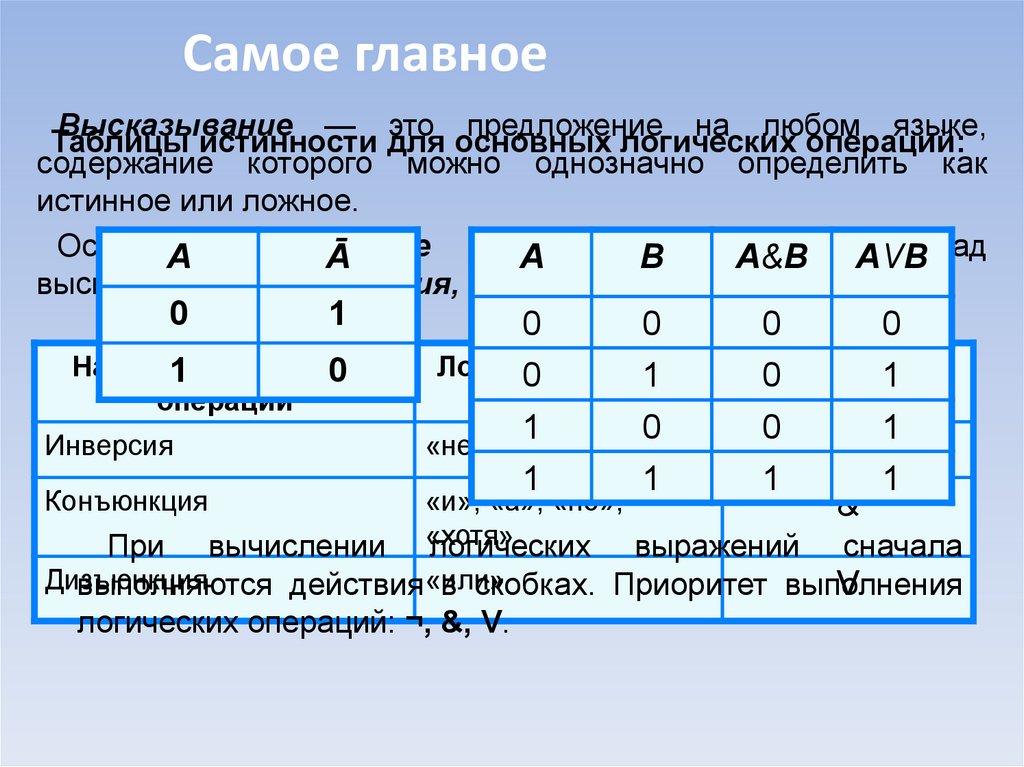
Самое главное
Высказывание — это предложение на любом языке,
Таблицы истинности для основных логических операций:
содержание которого можно однозначно определить как
истинное или ложное.
Основные
логические
операции,
А
Ā
A
B определённые
A&B AVB над
высказываниями: инверсия, конъюнкция, дизъюнкция.
0
1
Название
1 логической
0
операции
Инверсия
0
0
Логическая
связка
0
1
1
1
0
1
«не, «неверно, что»
Конъюнкция
0
0
Обозначение
0
1
0
1
¬, ─
1
1
«и», «а», «но»,
&
При вычислении «хотя»
логических выражений сначала
Дизъюнкция
выполняются действия «или»
в скобках. Приоритет выполнения
V
логических операций: ¬, &, V.