Квадратные неравенства и способы их решения

1.

АЛГЕБРА 8 КЛАСС
Большинство жизненных задач решаются как
алгебраические уравнения: приведением их к
самому простому виду.
Л. Н. Толстой

2.

Тема урока

3.

Цель урока:
научиться решать квадратные
неравенства с помощью графика
квадратичной функции

4.

«Никогда не беритесь за последующее,
не усвоив предыдущего»
И.П. Павлов

5.

Какие неравенства называются
квадратными?

6.

Квадратным неравенством
называют неравенство вида
ax2 + bx + c > 0
ax2 + bx + c < 0
ax2 + bx + c ≥ 0
ax2 + bx + c ≤ 0
где коэффициенты a, b, с
действительные числа (a ≠ 0)
–
любые

7.

Выберите неравенства, которые являются
квадратными
1) 3х2 + х + 5 > 0
4) 4х ≤ 5
2) 5х + 8 > 4
5) (2х+1)·40 < 16
3)
3х2
–1≤0
6) х2 – 4х + 5 ≤ 0

8.

Выберите неравенства, которые можно
свести к квадратным
1) 3х2 (x + 5) > 0
4) (х2 – 4)(х+5) ≤ 0
2) 5х+8 > х2
5) (2х+1)(3+4) < 16
3) 3х – 1 ≤ 0
6) (х – 4)(х+5) ≤ 0

9.

Что является графиком
функции
y=ax2+bx+c?

10.

Как определить, куда
направлены ветви параболы
(вверх или вниз)?

11.

Заполнить пустые клетки таблицы, указав
знаком или направление ветвей параболы.
Парабола
Направление
ветвей
параболы
y = 1- x2
y = 2x2+3x-1 y = -5x2 + x + 1

12.

Заполнить пустые клетки таблицы, указав
знаком или направление ветвей параболы.
Парабола
y = 1- x2
Направление
ветвей
параболы
y = 2x2+3x-1 y = -5x2 + x + 1

13.

Как определить, сколько
корней имеет квадратный
трехчлен?

14.

Формула нахождения
дискриминанта
D=b2-4ac

15.

Назовите известные способы
решения квадратных
уравнений?

16.

Устно найти корни уравнения
Ответ: х1 = 2, х2 = 3
x2 - 5x + 6 = 0

17.

Найти корни уравнения 6x2 - 7x – 3 = 0
Решение записать в тетради

18.

Как значение дискриминанта
влияет на количество точек
пересечения параболы с осью Ох?

19.

Назовите число корней уравнения
и знак
коэффициента a, если график соответствующей
квадратичной функции расположен следующим образом:

20.

число корней
уравнения ax2+bx+c=0
знак a
2
+
2
-
1)
2)
2)

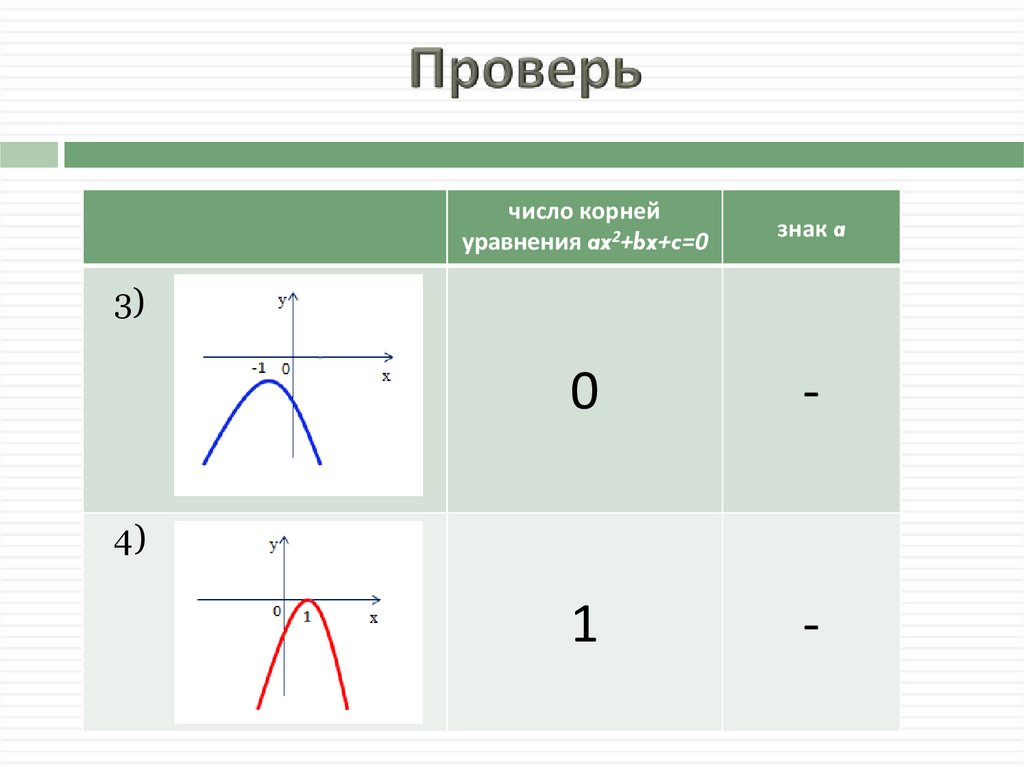
21.

число корней
уравнения ax2+bx+c=0
знак a
0
-
1
-
3)
2)
4)

22.

число корней
уравнения ax2+bx+c=0
знак a
0
+
1
+
5)
2)
6)

23.

у
Рассмотрим график
функции у = х2 - 5х + 6
При х= 2 и х= 3
При 2< х < 3
При х< 2 и х > 3
у=0
у<0
у >0
у>0
у>0
х2 - 5х +6 >0
х< 2 и х> 3
x (- ; 2) (3; + )
х2 - 5х +6 0
х 2иx 3
x (- ; 2] [3; + )
2
у<0
3
х

24.

у
Рассмотрим график
функции у = х2 - 5х + 6
При х= 2 и х= 3
При 2< х < 3
При х< 2 и х > 3
у=0
у<0
у >0
у>0
у>0
х2 - 5х +6 < 0
2< х < 3
х (2; 3)
х2 - 5х +6 0
2 х 3
х [2; 3]
2
у<0
3
х

25.

1. Найти действительные корни соответствующего
квадратного уравнения
2. Определить направление ветвей параболы по знаку
первого коэффициента квадратичной функции
3. Изобразить эскиз графика квадратичной функции,
используя точки пересечения (или касания) с осью Ох,
если они есть
4. По графику определить промежутки, на которых функция
принимает нужные значения

26.

Удачи вам!