Похожие презентации:
Многогранники. Понятие многогранника
1. Многогранники
Выполнили: Гриднева Альбина иТулупова Светлана
2.
Общие сведения:1.1. Проект подготовили: Гриднева Альбина и Тулупова Светлана
1.2. Руководитель: Васильева Надежда Леонидовна, учитель
математики
1.3. Учебное заведение: Московская область, г.Железнодорожный,
МБОУ гимназия №9 имени С.Г.Горшкова
1.4. Секция: «Что не открыл Архимед, откроем мы!»
1.5. Тема: Многогранники
3.
Цели проекта:• Систематизировать сведения о многогранниках;
• Создать учебное пособие для школьников, изучающих геометрию
на углублённом уровне.
• Повысить мотивацию учащихся к изучению геометрии.
Задачи:
1. Изучить теорию о многогранниках.
2. Подготовить слайды по теме для использования в урочной и во
внеурочной деятельности.
3. Создать модели различных многогранников для использования в
качестве наглядных пособий .
Гипотеза исследования: существует более широкий класс
многогранников, чем представленные в школьном курсе
стереометрии. Многогранники имеют определенные математические
взаимосвязи.
1.
2.
3.
4.
5.
6.
Краткое содержание:
Понятие многогранника.
Призма
Пирамида
Платоновы тела
Архимедовы тела
Звездчатые многогранники
4. Многогранники
5.
• Многогранник (Многогранная поверхность)поверхность, составленная из многоугольников иограничивающая некоторое геометрическое тело
6.
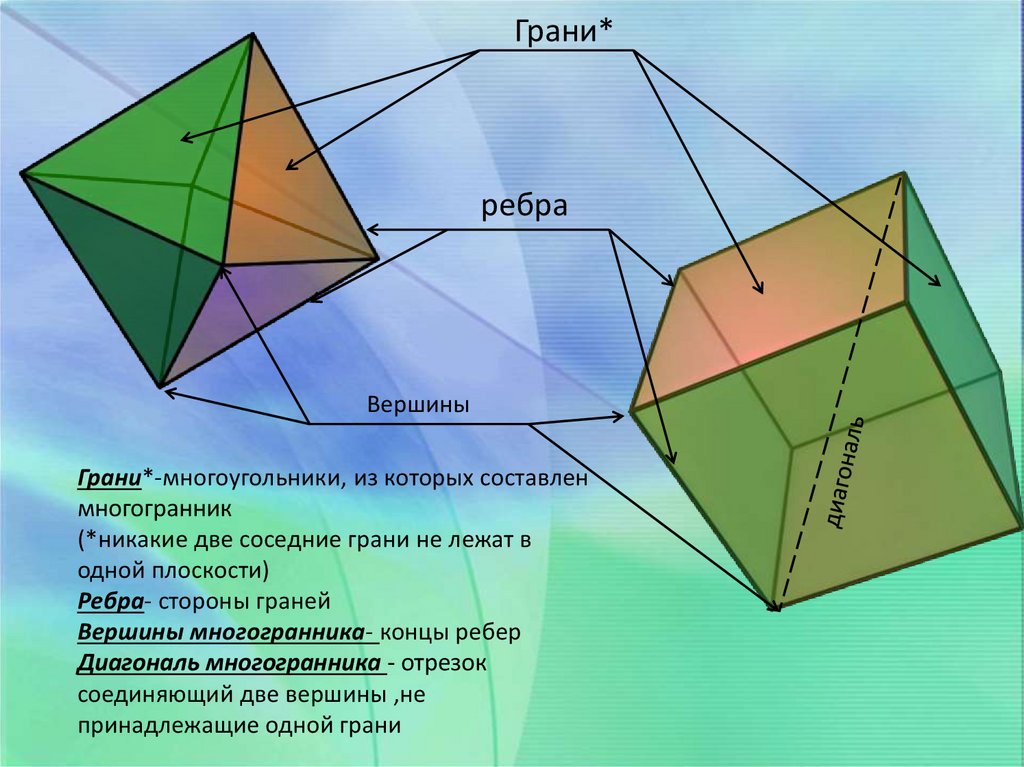
Грани*ребра
Вершины
Грани*-многоугольники, из которых составлен
многогранник
(*никакие две соседние грани не лежат в
одной плоскости)
Ребра- стороны граней
Вершины многогранника- концы ребер
Диагональ многогранника - отрезок
соединяющий две вершины ,не
принадлежащие одной грани
7.
многогранникВыпуклый
(если расположен по
одну сторону от
плоскости каждой его
грани)
В выпуклом
многограннике сумма
всех плоских углов при
каждой его вершине
меньше 360°
Невыпуклый
(найдется по крайней мере
одна грань такая, что
плоскость, проведенная через
эту грань, делит данный
многогранник на две или более
частей.)
8. Призма
Боковые гранивершины
Боковые
ребра
основания
• Многогранник,
составленный из двух равных
многоугольников, лежащих в
параллельных плоскостях, и
параллелограммов,
называется призмой.
9. Прямая призма
• Если боковые ребрапризмы перпендикулярны
к основаниям, то призма
называется прямой.
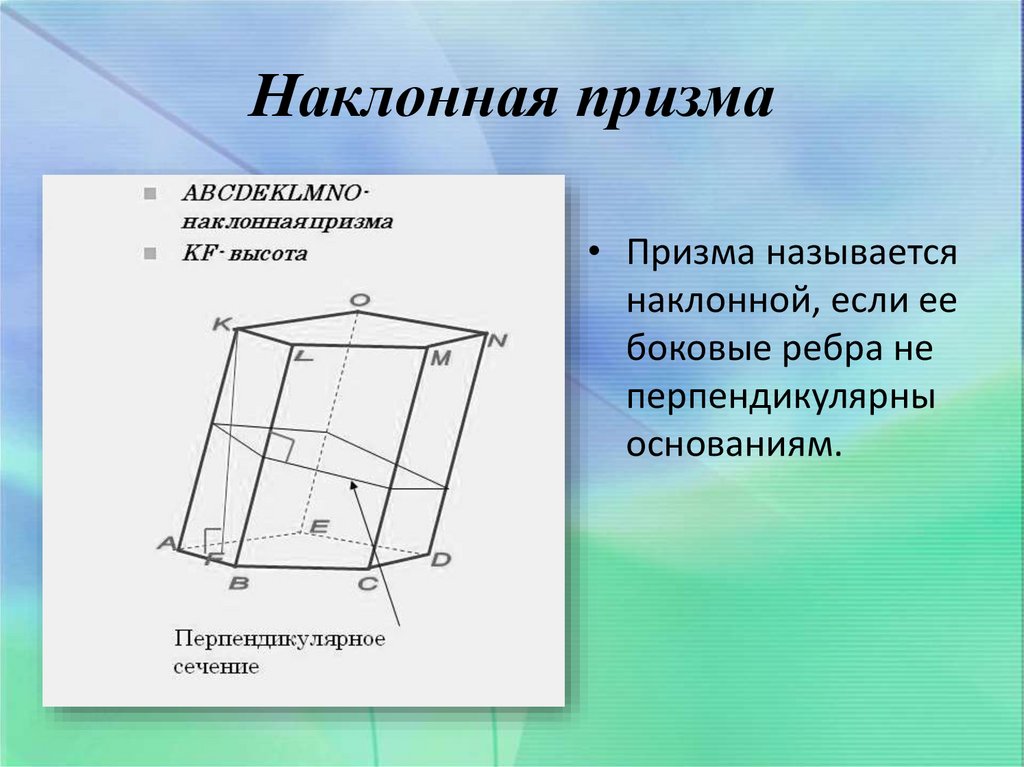
10. Наклонная призма
• Призма называетсянаклонной, если ее
боковые ребра не
перпендикулярны
основаниям.
11. Правильная призма
• Прямая призма, основанием которойслужит правильный многоугольник,
называется правильной призмой.
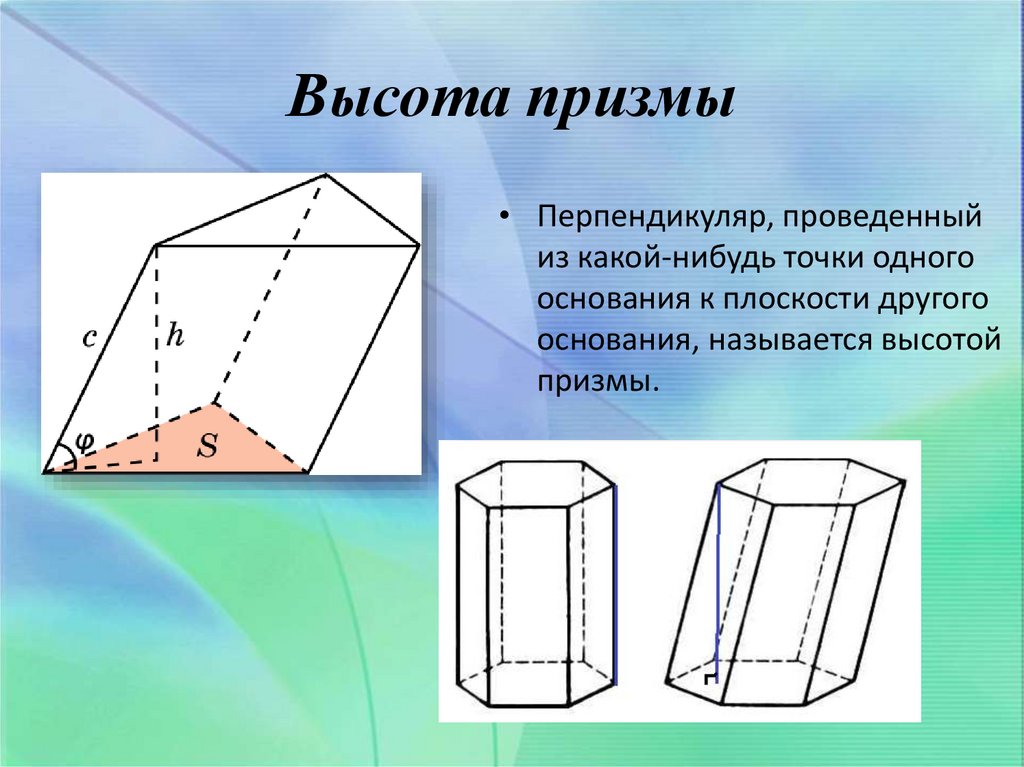
12. Высота призмы
• Перпендикуляр, проведенныйиз какой-нибудь точки одного
основания к плоскости другого
основания, называется высотой
призмы.
13. Площади полной и боковой поверхностей призмы
Площадью боковой поверхности призмы называется
сумма площадей её боковых граней.
• Площадью полной поверхности призмы называется сумма
площадей всех её граней.
• Площадь полной поверхности призмы (S) равна сумме
площади её боковой поверхности (Sб) и удвоенной
площади основания (2Sо):
S=Sб+2Sо
14.
• Теорема: Площадь боковой поверхностипрямой призмы равна произведению
периметра основания на высоту призмы.
Sб=Pо*h
•Площадь боковой поверхности
наклонной призмы (Sб) равна
произведению периметра сечения
призмы, перпендикулярного
боковому ребру, на длину бокового
ребра:
Sб=Pсеч*L
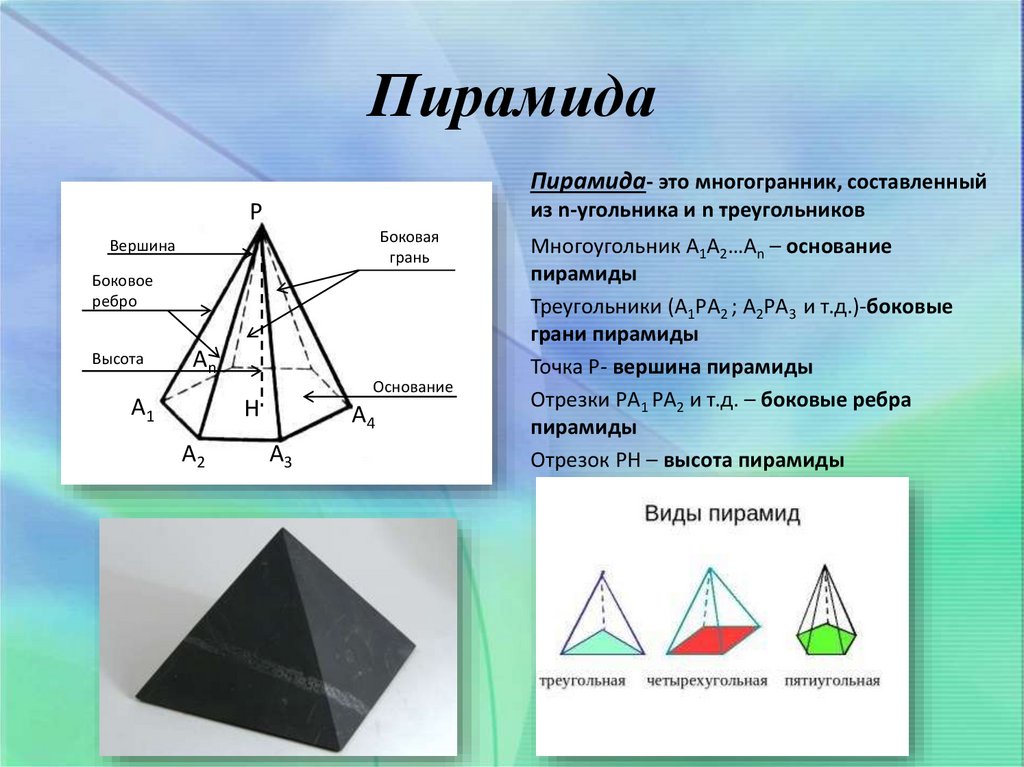
15. Пирамида
Пирамида- это многогранник, составленныйиз n-угольника и n треугольников
P
Боковая
грань
Вершина
Боковое
ребро
Высота
An
A1
Основание
H
A2
A4
A3
Многоугольник A1A2…An – основание
пирамиды
Треугольники (A1РA2 ; A2РA3 и т.д.)-боковые
грани пирамиды
Точка Р- вершина пирамиды
Отрезки РA1 РA2 и т.д. – боковые ребра
пирамиды
Отрезок РН – высота пирамиды
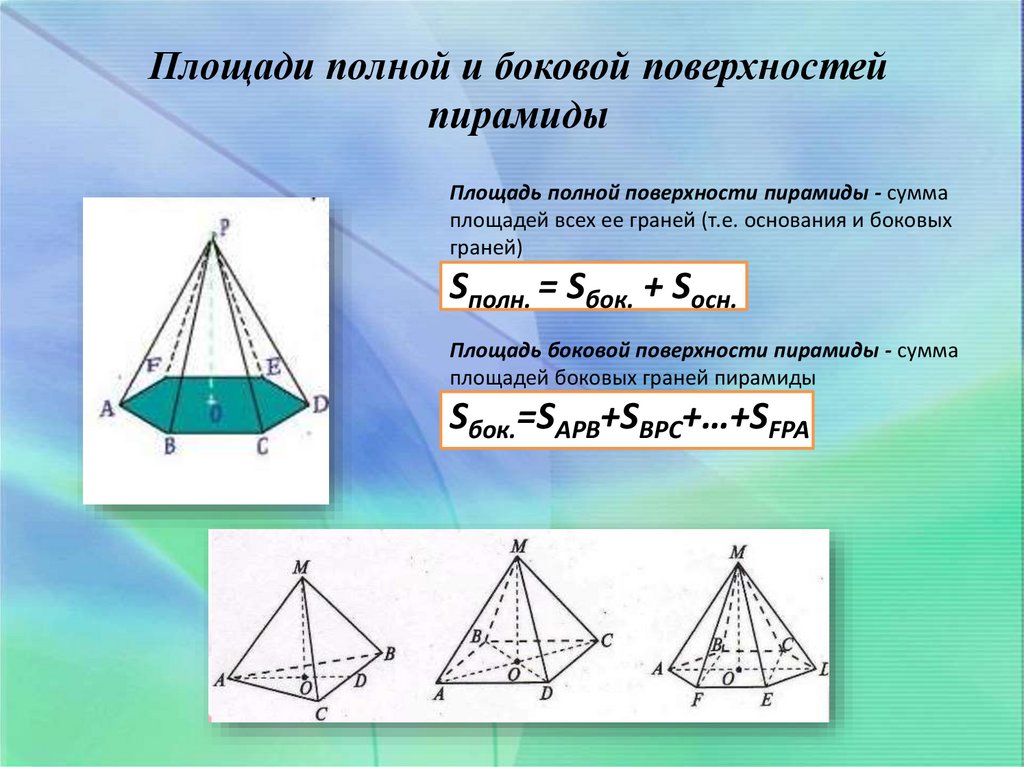
16.
Площади полной и боковой поверхностейпирамиды
Площадь полной поверхности пирамиды - сумма
площадей всех ее граней (т.е. основания и боковых
граней)
Sполн. = Sбок. + Sосн.
Площадь боковой поверхности пирамиды - сумма
площадей боковых граней пирамиды
Sбок.=SАРВ+SВРС+…+SFPA
17. Правильная пирамида
Пирамида называется правильной, если ееоснование – правильный многоугольник, а
отрезок, соединяющий вершину пирамиды с
центром основания*, является ее высотой
*Центром правильного многоугольника называется
центр вписанной в него/описанной около него
окружности
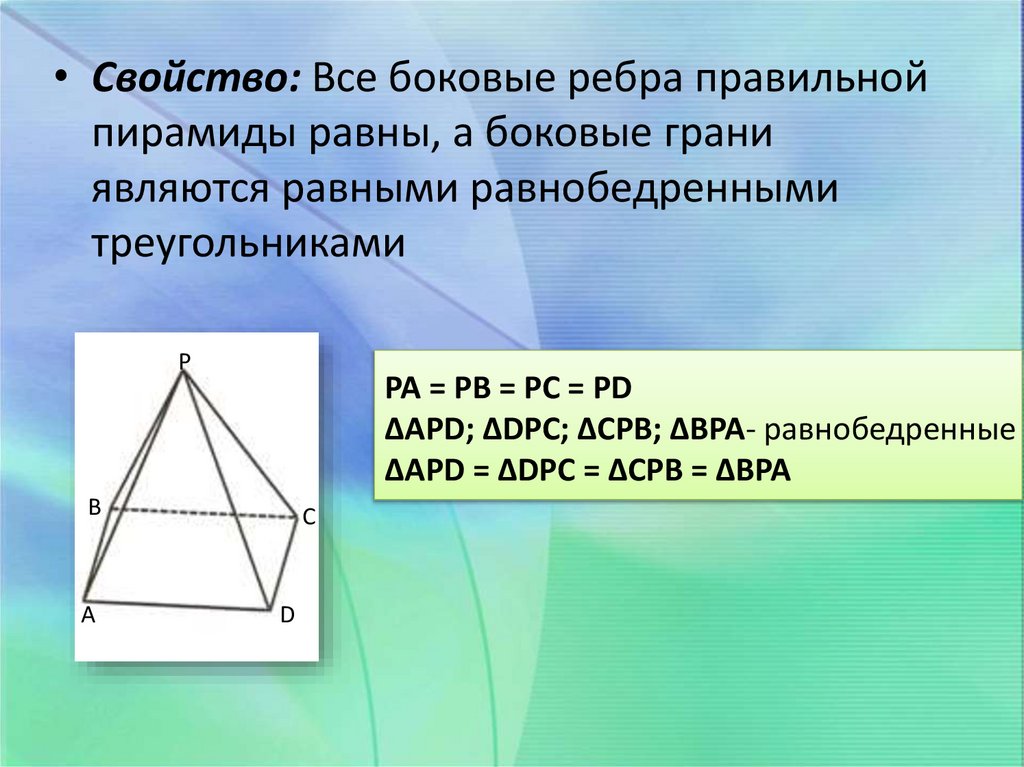
18.
• Свойство: Все боковые ребра правильнойпирамиды равны, а боковые грани
являются равными равнобедренными
треугольниками
P
PA = PB = PC = PD
ΔAPD; ΔDPC; ΔCPB; ΔBPA- равнобедренные
ΔAPD = ΔDPC = ΔCPB = ΔBPA
В
А
С
D
19.
• Теорема: Площадь боковой поверхностиправильной пирамиды равна половине
произведения периметра основания на
апофему*
*апофема-высота боковой грани правильной пирамиды, проведенная из ее
вершины
апофема
d
Sбок. = 1/2 Pосн. * d
20. Усеченная пирамида
Усеченная пирамида – многогранник, гранями которогоявляются n-угольники А1А2…Аn и В1В2…Вn (нижнее и верхнее
основания), расположенные в параллельных плоскостях, и
n четырехугольников А1А2B2B1, A2A3B3B2, …, AnA1B1B n
(боковые грани)
21.
• Свойство: боковые грани усеченнойпирамиды- трапеции
• Теорема: Площадь боковой поверхности
правильной усеченной пирамиды равна
произведению полусуммы периметров
оснований на апофему
l
22. Платоновы тела
Правильным называется
такой многогранник, все
грани которого равны (или
конгруэнтны) между собой
и при этом являются
правильными
многоугольниками.
(а)
(б)
(в)
(г)
(д)
Рис. Платоновы тела: (а) октаэдр («Огонь»), (б) гексаэдр или куб
(«Земля»),
(в) октаэдр («Воздух»), (г) икосаэдр («Вода»), (д) додекаэдр
(«Вселенский разум»)
23. Почему платоновы тела?
Правильные многогранники носят также название платоновых тел, т. к. занимают
важное место в философии Платона. Как и другие древние греки, он считал, что
существует 4 первоэлемента – земля, вода, воздух и огонь. Развивая пифагорейскую
концепцию о математическом устройстве Вселенной, Платон полагал, что каждый
элемент имеет форму того или иного правильного многогранника: земле как самому
устойчивому элементу соответствует куб, огню – самый «небольшой» многогранник с
самыми острыми вершинами и ребрами, то есть тетраэдр; воде соответствует икосаэдр,
а воздуху – октаэдр. Эти элементы – неделимые («атомы»), элементы могут
превращаться друг в друга по определенным законам, связанным с сохранением тех
треугольников, из которых сделаны: например, одно «тело» воздуха может
превратиться в два «тела» огня, а одно «тело» воды – в два «тела» воздуха и одно –
огня. (Сами треугольники при этом материальными не являются, поскольку плоские,
тогда как материальные тела должны быть трехмерными). Форма же всей Вселенной
соответствует пятому телу – додекаэдру. Таким образом, в пифагорейско-платоновском
космосе торжествует математическая гармония, выражаемая «золотым сечением»,
тесно связанным с правильным пятиугольником, который и лежит в основе додекаэдра.
24. Основными числовыми характеристиками платоновых тел является число граней F, число вершин V и число плоских углов E на
поверхности тела.Многогранник
F
E
Форма грани
Тетраэдр
4
4
6
Треугольник
Гексаэдр
6
8
12
Квадрат
Октаэдр
8
6
12
Треугольник
Икосаэдр
20
12
30
Треугольник
Додекаэдр
12
20
30
Пентагон
V
25. Архимедовы тела
Известно еще множество
совершенных тел, получивших
название полуправильных
многогранников или
Архимедовых тел. У них также
все многогранные углы равны и
все грани – правильные
многоугольники, но несколько
разных типов. Существует 13
полуправильных
многогранников, открытие
которых приписывается
Архимеду.
(а)
(б)
(в)
(г)
(д)
(е)
(ж)
(з)
(и)
Рис. Архимедовы тела: (а) усеченный тетраэдр, (б) усеченный куб, (в)
усеченный октаэдр, (г) усеченный додекаэдр, (д) усеченный икосаэдр
(е) кубооктаэдр, (ж) икосододекаэдр
(з) ромбокубооктаэдр, (и) ромбоикосододекаэдр
(к) курносый куб, (л) курносый додекаэдр
(к)
(л)
26.
Звёздчатые многогранникиКроме правильных и полуправильных многогранников
красивые формы имеют так называемые правильные
звездчатые многогранники. Они получаются из
правильных многогранников продолжением граней или
ребер.
Звёздчатый многогранник (звёздчатое тело) — это
невыпуклый многогранник, грани которого
пересекаются между собой. Как и у незвёздчатых
многогранников, грани попарно соединяются в рёбрах
(при этом внутренние линии пересечения не считаются
рёбрами).
Звёздчатой формой многогранника называется
многогранник, полученный путём продления граней
данного многогранника через рёбра до их следующего
пересечения с другими гранями по новым рёбрам.
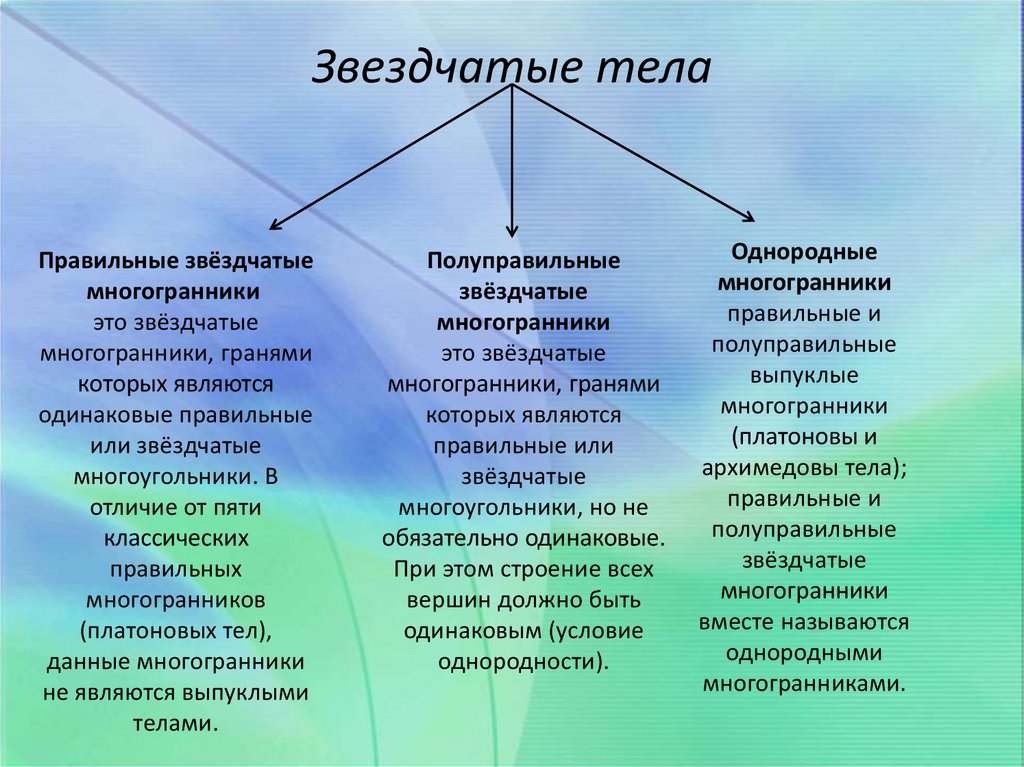
27. Звездчатые тела
Правильные звёздчатыемногогранники
это звёздчатые
многогранники, гранями
которых являются
одинаковые правильные
или звёздчатые
многоугольники. В
отличие от пяти
классических
правильных
многогранников
(платоновых тел),
данные многогранники
не являются выпуклыми
телами.
Полуправильные
звёздчатые
многогранники
это звёздчатые
многогранники, гранями
которых являются
правильные или
звёздчатые
многоугольники, но не
обязательно одинаковые.
При этом строение всех
вершин должно быть
одинаковым (условие
однородности).
Однородные
многогранники
правильные и
полуправильные
выпуклые
многогранники
(платоновы и
архимедовы тела);
правильные и
полуправильные
звёздчатые
многогранники
вместе называются
однородными
многогранниками.
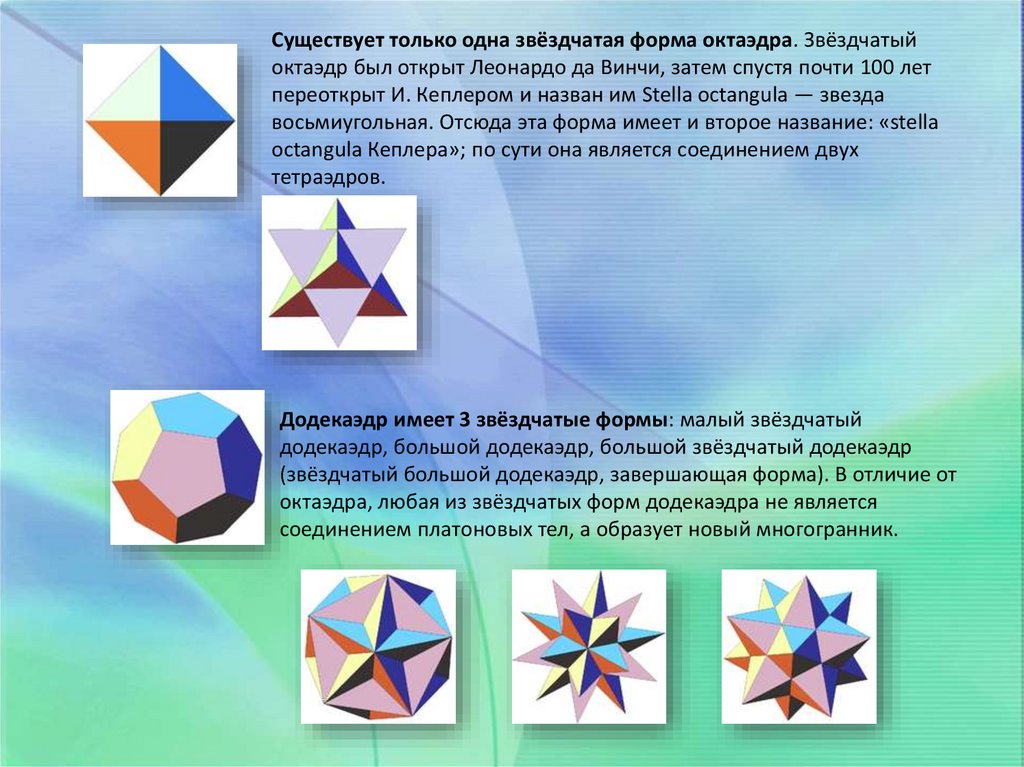
28.
Существует только одна звёздчатая форма октаэдра. Звёздчатыйоктаэдр был открыт Леонардо да Винчи, затем спустя почти 100 лет
переоткрыт И. Кеплером и назван им Stella octangula — звезда
восьмиугольная. Отсюда эта форма имеет и второе название: «stella
octangula Кеплера»; по сути она является соединением двух
тетраэдров.
Додекаэдр имеет 3 звёздчатые формы: малый звёздчатый
додекаэдр, большой додекаэдр, большой звёздчатый додекаэдр
(звёздчатый большой додекаэдр, завершающая форма). В отличие от
октаэдра, любая из звёздчатых форм додекаэдра не является
соединением платоновых тел, а образует новый многогранник.
29.
Икосаэдр имеет 59 звёздчатых форм, из которых 32 обладают полной, а 27 —неполной икосаэдральной симметрией. Одна из этих звёздчатых форм (20-я,
модель 41 по Веннинджеру), называемая большим икосаэдром, является
одним из четырёх правильных звёздчатых многогранников Кеплера —
Пуансо. Его гранями являются правильные треугольники, которые сходятся в
каждой вершине по пять; это свойство является у большого икосаэдра общим
с икосаэдром.
Среди звёздчатых форм также имеются: соединение пяти
октаэдров, соединение пяти тетраэдров, соединение десяти
тетраэдров. Первая звёздчатая форма — малый триамбический
икосаэдр.
Если каждую из граней продолжить неограниченно, то тело будет окружено
большим многообразием отсеков — частей пространства, ограниченных
плоскостями граней. Все звёздчатые формы икосаэдра можно получить
добавлением к исходному телу таких отсеков. Большой икосаэдр состоит из
всех этих кусков, за исключением последних шестидесяти. Следующая
звёздчатая форма — завершающая.
30.
Кубооктаэдр имеет 4 звёздчатые формы, удовлетворяющиеограничениям, введённым Миллером. Первая из них является
соединением куба и октаэдра.
Икосододекаэдр имеет множество звёздчатых форм, первая из
которых есть соединение икосаэдра и додекаэдра..
Икосододекаэдр имеет 32 грани, из которых 12 являются правильными
пятиугольными гранями, а остальные 20 — правильными треугольниками.
31. Развертки многогранников
Звёздчатый октаэдрКубо-октаэдр
Икосо-додекаэдр
32. Некоторые модели, выполненные авторами
33. Выводы
• Работая над проектом, мы:узнали новые виды многогранников;
научились делать модели многогранников;
подготовили слайды о многогранниках для использования в
урочной и во внеурочной деятельности;
• узнали, что в микромире многогранники встречаются в виде
молекул, вирусов и бактерий - простейших организмов. В различных
областях человеческой деятельности можно встретиться с
многогранниками: химии, технике, архитектуре, дизайне,
декоративном искусстве и др.
Многогранники привлекают взгляд своей
гармоничностью и совершенством.
И в их мире ещё есть место для открытий !
34. Многогранники вокруг нас
В природеВ искусстве
В архитектуре
35. Используемые информационные ресурсы:
• http://mnogogranniki.ru/vidy-mnogogrannikov.html• https://ru.wikipedia.org/wiki
• Учебник « Геометрия 10-11 класс»,
Авторы: Л.С.Атанасян, В.Ф.Бутузов, С.Б. Кадомцев, Л.С.Киселёв,
Э.Г.Позняк
• Энциклопедия для детей Аванта+



























 Математика
Математика








