Похожие презентации:
Системный анализ и принятие решений. Основы оптимального управления. Задача линейного программирования
1.
Системный анализ и принятиерешений.
Основы оптимального управления
Задача линейного программирования
2.
ЗАДАЧИ ЛИНЕЙНОГО ПРОГРАММИРОВАНИЯ (ЗЛП)Постановка и математическая модель
Методы решения
Экономический анализ результатов решения
ЗЛП специального вида
Постановка и математическая модель
Опр. Математическая модель – это математическое описание (с помощью
формул и неравенств) некоторого процесса или объекта.
1 1
n
n
→
Опр. Общей задачей линейного программирования (планирования) называется
задача отыскания оптимального решения
Х =( х1 , х2 , , хn )
Х =( х j )
такого, что
F = ∑ c j x j max( min )
F( X ) = c x + ... + c x
max( min )
→
при ограничениях
a11 x1 + ... + a1n x n ≤b1
..............................
a m1 x1 + ... + a mn x n ≤bm
x j ≥0, ∀j =1,2,..., n
∑aij x j ≤bi
x j ≥0
(1.1)
Слайд 2
3.
Неизвестные Х = ( х1 , х 2 , , х n ) , изменяя которые можно совершенствоватьсистему, называются управляющими переменными.
Опр. Совокупность неизвестных Х =( х1 , х2 , , хn ) , называется
допустимым
решением (планом) задачи, если они удовлетворяют системе ограничений (1.1)
Опр. Ограничения (1.1) характеризуют имеющиеся
возможности для выбора решения, называются
функциональными и задают область допустимых
решений D
Опр. Максимизируемая (минимизируемая) линейная функция F( X ) = c1 x1 + ... + c n x n
называется целевой функцией задачи.
Она представляет собой принятый критерий эффективности решения задачи,
соответствующий поставленной цели.
Допустимый план, доставляющий экстремальное значение (max, min) целевой
функции, называется оптимальным.
Рассмотренная модель ЗЛП является линейной, т.к. ее основу составляют
выражения линейного типа. Термин «программирование» означает поиск
оптимальной программы (решения).
Слайд 3
4.
ЗамечаниеПри решении задач математического программирования возможны особые
случаи:
Область допустимых решений является пустым множеством
(ограничения противоречивы).
Целевая функция является неограниченной на области допустимых
решений (математическая модель разработана некорректно и некоторые
существенные ограничения в ней отсутствуют).
Задача имеет множество решений, равноценных между собой, но
оптимальных по сравнению с другими допустимыми решениями.
Слайд 4
5.
Задачиоптимального
программирования
в
наиболее
общем
виде
классифицируют по следующим признакам.
1. По характеру взаимосвязи между переменными
a ) линейные,
б) нелинейные.
2. По характеру изменения переменных
а) непрерывные,
б) дискретные.
3. По учёту фактора времени
а) статические,
б) динамические.
4. По наличию информации о переменных
а) задачи в условиях полной определённости (детерминированные),
б) задачи в условиях неполной информации,
в) задачи в условиях неопределённости.
5. По числу критериев оценки альтернатив
а) однокритериальные задачи,
б) многокритериальные задачи.
Слайд 5
6.
Рассмотрим математические модели некоторых важных экономических задач.Задача об использовании ресурсов (задача планирования производства).
Для производства 2-х видов продукции Р1 и Р2 используют 4 вида ресурсов
r1, r2, r3 и r4. Запасы ресурсов и их расход для изготовления единицы продукции
каждого вида приведены в таблице:
Вид
ресурса
r1
r2
r3
r4
Количество ед. ресурса для
изготовления ед. продукции
Р1
Р2
1
2
3
3
1
1
-
Запас
ресурса
18
16
5
21
Прибыль, получаемая от реализации единицы продукции Р1 и Р2, равна
соответственно 2 и 3 ден. ед.
Требуется составить математическую модель задачи с целью найти такой
план производства продукции, при котором прибыль от ее реализации будет
наибольшей.
Слайд 6
7.
Решение.Для построения математической модели необходимо:
1. Введем управляющие переменные:
обозначим
x1 – количество единиц продукции Р1,
x2 – количество единиц продукции Р2.
По смыслу задачи переменные неотрицательны: x1 ≥0 , x 2 ≥0.
→
2. Построим функцию цели.
Прибыль от реализации продукции Р1 составит 2x1 ден. ед.,
прибыль от реализации продукции Р2 составит 3x 2 ден. ед.
Функция цели - суммарная прибыль - должна быть максимальной и описывается
выражением: F = 2 x1 +3 x 2 max
3. Построим систему функциональных ограничений.
Расход каждого ресурса для изготовления продукции Р1 и Р2 в количестве x1 и
x2 соответственно описывается выражением:
1x1 +3 x 2
ресурса r1 ресурса r2 -
2 x1 +1x 2
ресурса r3 -
0 x1 +1x 2
ресурса r4 -
3 x1 + 0 x 2
Слайд 7
8.
Потребление ресурсов не должно превышать их запасов, поэтому связь междупотреблением и запасами ресурсов выразится системой неравенств:
x1 + 3 x 2 ≤18
2 x1 + x 2 ≤16
x 2 ≤5
3 x1 ≤21
Найти такой план выпуска продукции
X =( x1 , x 2 )
при котором прибыль максимальна
F = 2 x1 +3 x 2
и выполнены ограничения
→
Таким образом, математическая модель задачи построена:
max
x1 + 3 x 2 ≤18
2 x1 + x 2 ≤16
x 2 ≤5
3 x1 ≤21
x1 ≥0 , x 2 ≥0
Слайд 8
9.
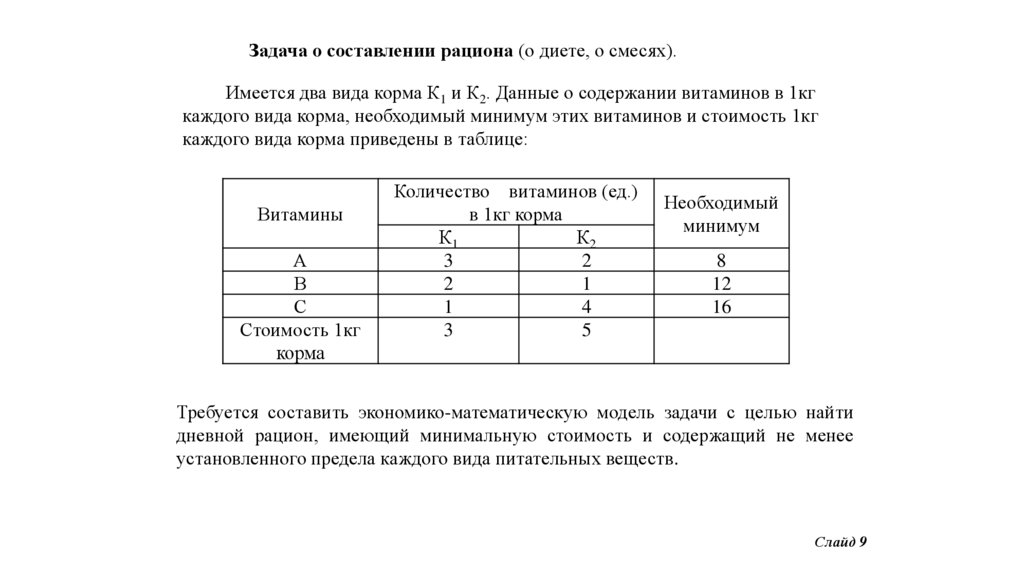
Задача о составлении рациона (о диете, о смесях).Имеется два вида корма К1 и К2. Данные о содержании витаминов в 1кг
каждого вида корма, необходимый минимум этих витаминов и стоимость 1кг
каждого вида корма приведены в таблице:
Витамины
А
В
С
Стоимость 1кг
корма
Количество витаминов (ед.)
в 1кг корма
К1
К2
3
2
2
1
1
4
3
5
Необходимый
минимум
8
12
16
Требуется составить экономико-математическую модель задачи с целью найти
дневной рацион, имеющий минимальную стоимость и содержащий не менее
установленного предела каждого вида питательных веществ.
Слайд 9
10.
Решение.1. Введем управляющие переменные:
Обозначим - x1 , x2 - количество кормов К1 и К2, входящих в дневной рацион.
По смыслу переменные неотрицательны: x1 ≥0 , x 2 ≥0.
→
2. Функция цели - общая стоимость дневного рациона питания – описывается
выражением F = 3x1 +5 x2
и должна быть минимальной:
F = 3 x1 +5 x2 min
3. Построим ограничений.
Рацион будет включать следующие количества витаминов:
3x1 + 2 x2 единиц витамина А,
2 x1 +1x2
единиц витамина В,
1x1 + 4 x2
единиц витамина С.
Учитывая установленные пределы содержания питательных веществ, получим
систему неравенств:
3x1 + 2 x2 ≥8
2 x1 + x2 ≥12
x1 + 4 x2 ≥16
Слайд 10
11.
Таким образом, экономико-математическая модель задачи получена:X = ( x1 , x 2 ),
стоимость которого минимальна
F = 3 x1 +5 x2
и выполнены заданные ограничения
→
Составить дневной рацион
min
3x1 + 2 x2 ≥8
2 x1 + x2 ≥12
x1 + 4 x2 ≥16
x1 ≥0 , x 2 ≥0
Слайд 11
12.
Графический метод решения ЗЛПF ( x1 , x2 ) = c1 x1 + c2 x2
найти
при ограничениях
→
Рассмотрим ЗЛП с двумя переменными в стандартной форме:
max
a11 x1 + a12 x2 ≤b1 ,
a21 x1 + a22 x2 ≤b2 ,
,
...
am1 x1 + am 2 x2 ≤bm
x1 ≥0 , x2 ≥0.
Алгоритм решения ЗЛП графическим методом
Графический способ решения состоит из следующих этапов:
1.
Строится многоугольная область допустимых решений ЗЛП – ОДР
2.
Строится целевая функция – линия уровня
3.
Строится вектор-градиент целевой функции
4.
Выбирается оптимальное решение.
Слайд 12
13.
• Теорема1. Множество всех допустимых решений системы ограничений ЗЛПявляется выпуклым и представляет собой выпуклый многогранник
(многогранник решений).
а) является выпуклым
б) не является выпуклым
• Теорема2. Если ЗЛП имеет оптимальное решение, то целевая функция
принимает оптимальное (максимальное или минимальное) значение в одной из
угловых точек многогранника решений. Если целевая функция принимает
оптимальное значение более чем в одной угловой точке, то она принимает его в
любой точке, являющейся выпуклой линейной комбинацией этих точек
(геометрически это представляет случай, когда прямая целевой функции
совпадает с одной из граней ОДР).
• Теорема3. Каждому допустимому базисному решению ЗЛП соответствует
угловая точка многогранника решений, и наоборот, каждой угловой точке
многогранника решений соответствует допустимое базисное решение.
Следствие из теорем 2 и 3.
Оптимум целевой функции ЗЛП следует искать среди конечного числа ее
допустимых базисных решений.
Слайд 13
14.
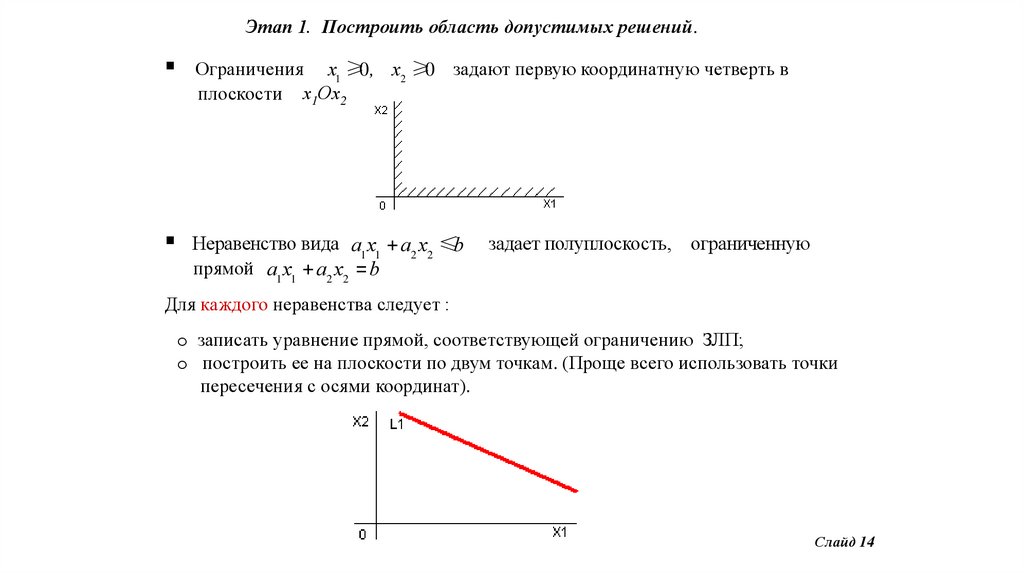
Этап 1. Построить область допустимых решений.Ограничения x1 ≥0 , x2 ≥0 задают первую координатную четверть в
плоскости х1Ох2
Неравенство вида a1 x1 + a2 x2 ≤b
прямой a1 x1 + a2 x2 = b
задает полуплоскость, ограниченную
Для каждого неравенства следует :
o записать уравнение прямой, соответствующей ограничению ЗЛП;
o построить ее на плоскости по двум точкам. (Проще всего использовать точки
пересечения с осями координат).
Слайд 14
15.
o выбрать на плоскости произвольную контрольную точку (КТ) A( x1 A ; x2 A ) иподставить ее координаты в правую часть неравенства a1 x1 A + a2 x2 A ≤b
.
Если неравенство верно, то искомая
полуплоскость находится с той же
стороны, что и контрольная точка:
В противном случае искомая
полуплоскость лежит с
противоположной стороны от прямой.
Замечание:
В качестве контрольной точки удобно брать О(0;0), т.е. x1 = 0, x 2 = 0.
Вместо начала координат можно использовать любую другую точку,
не лежащую на данной прямой.
Слайд 15
16.
Область пересечения всех найденных полуплоскостей определяетобласть допустимых решений D задачи.
Этап 2. Построить линию
уровня
F = c1 x1 +c2 x2
Рассмотрим целевую функцию
Выберем произвольное значение этой функции, например,
F =a
Тогда L : c x +c x = a уравнение прямой
0
1 1
2 2
линии (линии нулевого уровня), в точках
которой функция имеет одно и то же
постоянное (нулевое) значение.
Можно взять a = 0
Слайд 16
17.
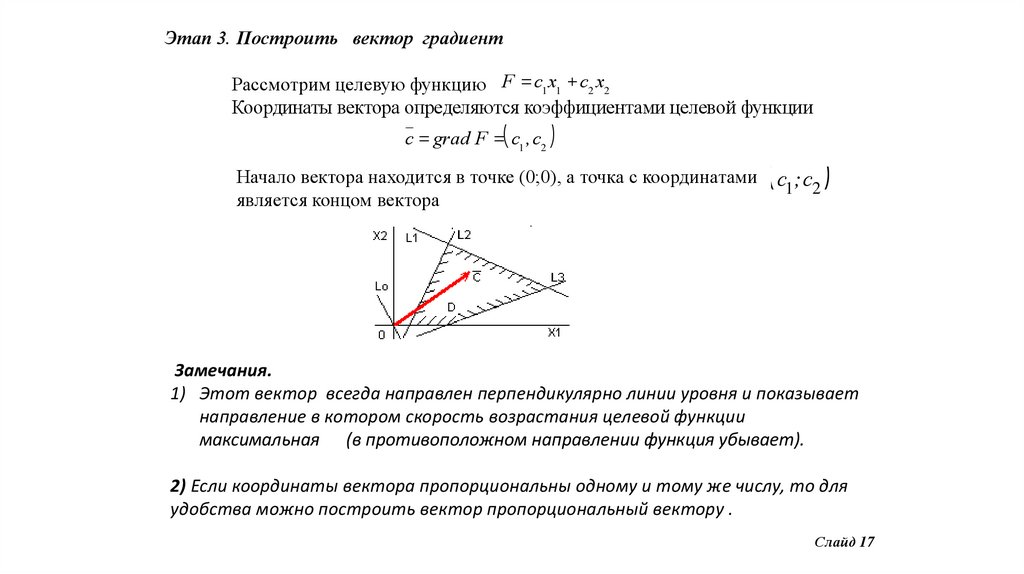
Этап 3. Построить вектор градиентРассмотрим целевую функцию F = c1 x1 + c2 x2
Координаты вектора определяются коэффициентами целевой функции
(
c = grad F = c1 , c2
)
Начало вектора находится в точке (0;0), а точка с координатами
является концом вектора
( c1; c2 )
.
Замечания.
1) Этот вектор всегда направлен перпендикулярно линии уровня и показывает
направление в котором скорость возрастания целевой функции
максимальная (в противоположном направлении функция убывает).
2) Если координаты вектора пропорциональны одному и тому же числу, то для
удобства можно построить вектор пропорциональный вектору .
Слайд 17
18.
Этап 4. Выбрать оптимальное решениеЕсли целевая функция ЗЛП ограничена на многограннике решений, то
существует такая угловая точка многогранника решений, в которой ЦФ достигает
своего оптимума.
При нахождении максимума целевой функции F ( x1 , x2 линию
уровня L0
)
надо передвигать параллельно самой себе в направлении вектораc до тех
пор, пока она не покинет пределов области допустимых решений D. Предельная
точка области при таком движении и является точкой максимума целевой
функции (точка М).
При нахождении минимума целевой функции линию уровня L0 надо
передвигать в направлении противоположном вектору градиенту c до
достижения предельной точки многоугольника. Точка К является точкой
минимума целевой функции.
Слайд 18
19.
(Координаты найденной предельной точки соответствуют оптимальному плану x1 , x2
*
*
*
*
Для нахождения значений переменных x1 и x2 достаточно решить систему
уравнений прямых, пересечением которых она является.
Подставляя найденные координаты в целевую функцию, получаем
экстремальное значение F * = c1 x* + c 2 x* , соответствующее оптимальному плану
x1* , x2*
(
)
1
2
Замечание. Недостатками графического метода являются:
• невозможность его применения к решению задач с тремя и более
неизвестными;
• необходимость выполнения аккуратного чертежа с соблюдением масштаба,
параллельности и перпендикулярности прямых.
Слайд 19
)
20.
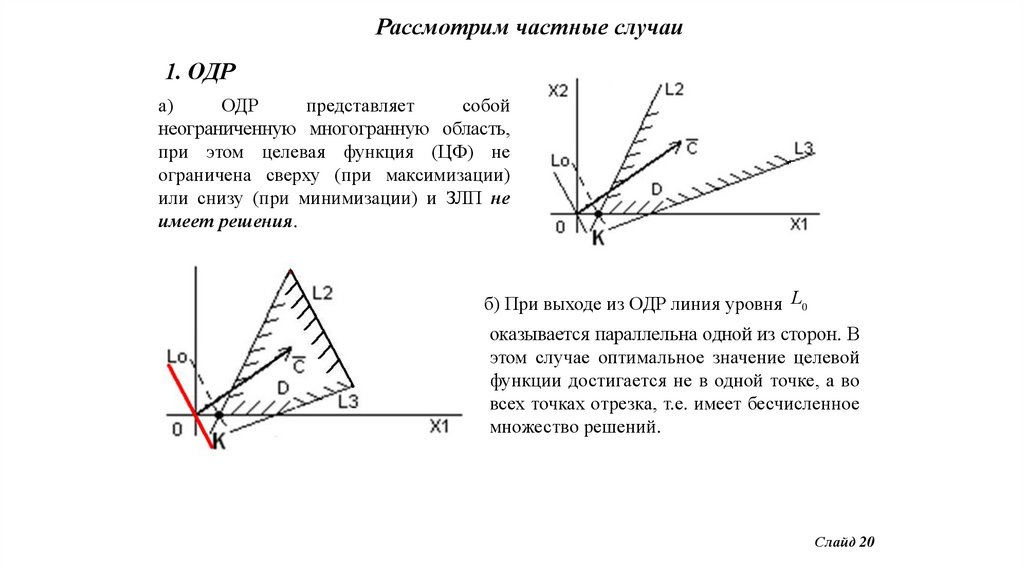
Рассмотрим частные случаи1. ОДР
а)
ОДР
представляет
собой
неограниченную многогранную область,
при этом целевая функция (ЦФ) не
ограничена сверху (при максимизации)
или снизу (при минимизации) и ЗЛП не
имеет решения.
б) При выходе из ОДР линия уровня L0
оказывается параллельна одной из сторон. В
этом случае оптимальное значение целевой
функции достигается не в одной точке, а во
всех точках отрезка, т.е. имеет бесчисленное
множество решений.
Слайд 20
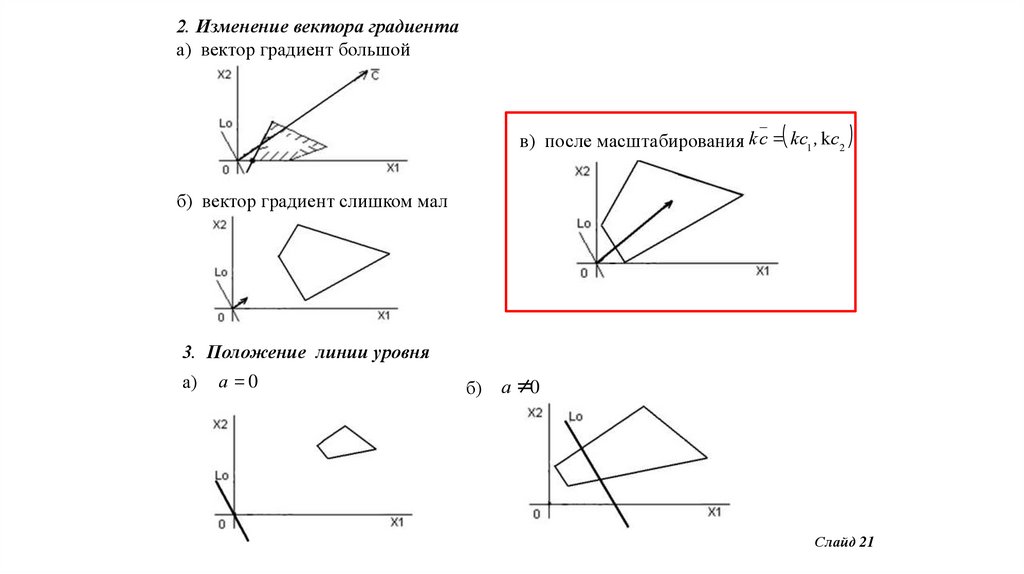
21.
2. Изменение вектора градиентаа) вектор градиент большой
(
в) после масштабирования k c = kc1 , kc2
)
б) вектор градиент слишком мал
3. Положение линии уровня
а)
a =0
б)
a ≠0
Слайд 21
22.
Задача.Найти
при ограничениях
F = 3x1 +1x2
→
Рассмотрим пример графического решения ЗЛП по заданной
математической модели
max
x1 + 2 x 2 ≤10
x1 + 2 x 2 ≥3
2 x1 + x 2 ≤11
x 2 ≤4
x1 ≥0, x 2 ≥0.
Решение.
1. Построим область допустимых решений
Ограничения x1 ≥0 , x2 ≥0 задают первую координатную четверть плоскости x1Ox2
Определим полуплоскость, соответствующую каждому неравенству
Неравенство x1 + 2 x2 ≤10 определяет полуплоскость,
ограниченную прямой L1 : x1 + 2 x2 =10
Она проходит через точки (0; 5) и (10; 0).
В качестве контрольной точки возьмем О(0;0), т.е.
x1 = 0 , x2 = 0 и подставим ее координаты в правую
часть неравенства: 0 ≤10 - истина, значит искомая
полуплоскость находится с той же стороны, что и
точка.
Слайд 22
23.
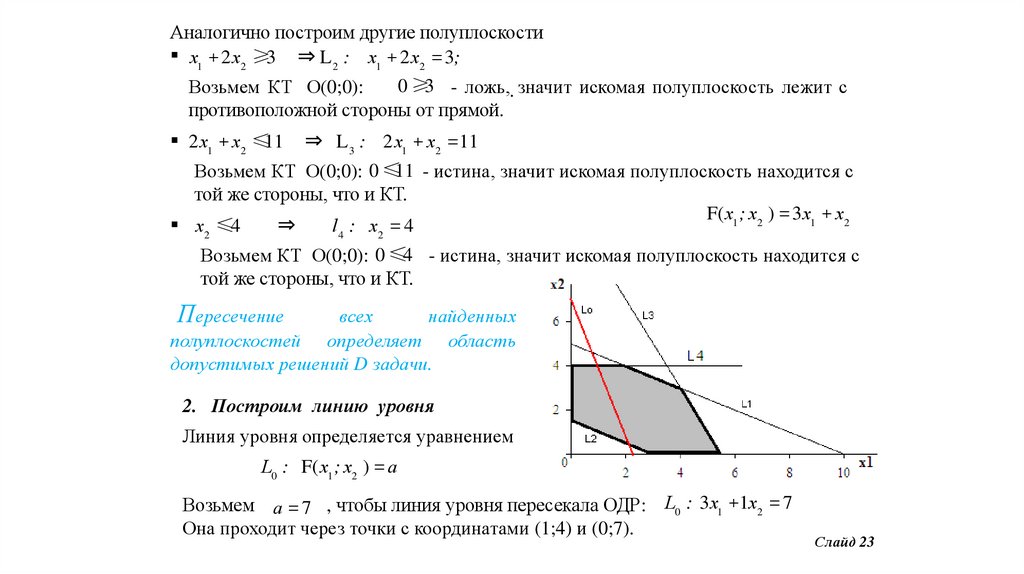
Аналогично построим другие полуплоскостиx1 + 2 x2 ≥3 ⇒ L 2 : x1 + 2 x2 = 3;
0 ≥3 - ложь,. значит искомая полуплоскость лежит с
Возьмем КТ О(0;0):
противоположной стороны от прямой.
2 x1 + x2 ≤11
⇒ L 3 : 2 x1 + x2 =11
Возьмем КТ О(0;0): 0 ≤11 - истина, значит искомая полуплоскость находится с
той же стороны, что и КТ.
F( x1 ; x2 ) = 3 x1 + x2
x2 ≤4
⇒
l 4 : x2 = 4
Возьмем КТ О(0;0): 0 ≤4 - истина, значит искомая полуплоскость находится с
той же стороны, что и КТ.
Пересечение
всех
найденных
полуплоскостей определяет область
допустимых решений D задачи.
2. Построим линию уровня
Линия уровня определяется уравнением
L0 : F( x1 ; x2 ) = a
Возьмем a = 7 , чтобы линия уровня пересекала ОДР: L0 : 3x1 +1x2 = 7
Она проходит через точки с координатами (1;4) и (0;7).
Слайд 23
24.
3. Построим вектор градиентКоординаты вектора определяются коэффициентами целевой функции F = 3 x1 +1x2
c =( 3,1)
Начало вектора находится в точке (0;0), а точка с координатами (3;1) является
концом вектора.
4. Найдем оптимальное решение
При нахождении максимума целевой функции линию уровня
передвигается параллельно самой себе в направлении вектора
до тех
пор,
пока не покинет пределов области допустимых решений D. Точка М является
является точкой максимума целевой функции.
Найдём координаты
2 x1 точки
+ x2 =М:
11
x1 = 5,5
M = L3 ∩( Ox1 ) ⇒
⇒ x =0
x2 = 0
2
Значение целевой функции в точке
M ( 5,5; 0 ) равно
Fmax ( M ) 3 5,5 1 0 16,5
Ответ:
Максимальное значение функции равно max F ( X ) =16,5 и
*
*
достигается при x1 = 5,5 и x2 = 0 .
Слайд 24


















 Математика
Математика








