Похожие презентации:
Сопротивление материалов
1.
РОССИЙСКИЙ ГОСУДАРСТВЕНЫЙ УНИВЕРСИТЕТ НЕФТИ И ГАЗА имени И.М. ГУБКИНА1
КАФЕДРА ТЕХНИЧЕСКОЙ МЕХАНИКИ
СОПРОТИВЛЕНИЕ МАТЕРИАЛОВ
2.
Литература2
Феодосьев В.И.
Сопротивление материалов: Учебное издание. – М: Изд-во МГТУ им.
Н.Э. Баумана, 2000. – 591 с.
Беляев Н.М.
Сопротивление материалов: Учебник. – М: Государственное изд-во
технико-теоретической литературы, 1958. – 856 с.
Писаренко Г.С., Яковлев А.П., Матвеев В.В.
Справочник по сопротивлению материалов: Справочное издание. – Киев:
Изд-во «Наукова Думка», 1988. – 734 с.
Романенко С.В.
Курс лекций по дисциплине «Сопротивление материалов»: Учебнометодическое пособие. – М: Изд-во «Нефть и газ», 2008. – 147 с.
3.
ЛЕКЦИЯ№13
Сопротивление материалов изучает методы расчета отдельных элементов
конструкций и сооружений на прочность, жесткость и устойчивость. Такие
расчеты необходимы, чтобы проектировать надежные и долговечные
конструкции при минимальной затрате материалов для их изготовления.
Прочность – это способность тела, не разрушаясь, сопротивляться воздействию
внешних сил.
Жесткость – это способность тела сопротивляться деформации (изменению формы и
размеров тела) при воздействии внешних сил, то есть способность конструкции или
элемента воспринимать нагрузку без существенного изменения геометрических
размеров.
Устойчивость – это способность тела сохранить исходную форму равновесия в
нагруженном состоянии (признак потери устойчивости – смена одной формы
равновесия другой формой равновесия).
4.
ВВЕДЕНИЕ4
Основные понятия сопротивления материалов опираются на законы и теоремы общей
механики и в первую очередь на законы статики.
Необходимо отметить, что первые заметки о прочности упоминаются в записках известного
художника ЛЕОНАРДО Де ВИНЧИ, а начало науки о сопротивлении материалов связывают с
именем знаменитого физика, математика и астронома ГАЛИЛЕО ГАЛИЛЕЯ.
В 1660 году Р. ГУК сформулировал закон, устанавливающий связь между нагрузкой и
деформацией: «Какова сила – таково и действие».
В XVIII веке необходимо отметить работы Л.ЭЙЛЕРА по устойчивости конструкций.
XIX – XX века являются временем наиболее интенсивного развития науки в связи с общим
бурным ростом строительства и промышленного производства при безусловно огромном
вкладе ученых-механиков России.
Итак, мы будем заниматься твердыми деформированными телами с изучением их
физических свойств.
5.
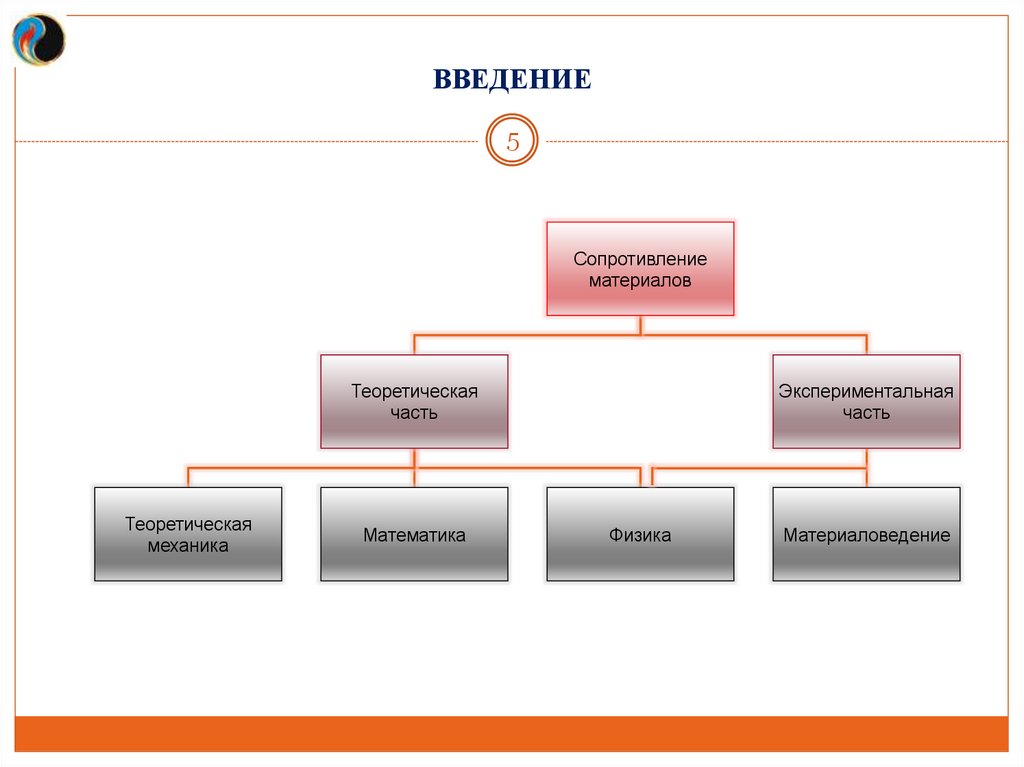
ВВЕДЕНИЕ5
Сопротивление
материалов
Теоретическая
часть
Теоретическая
механика
Математика
Экспериментальная
часть
Физика
Материаловедение
6.
СТРУКТУРА ДИСЦИПЛИН МЕХАНИЧЕСКОГО ЦИКЛА6
Физика
твердого тела
Сопротивление
материалов
Строительная
механика
разрушений
Механика твердого
деформируемого тела
Теория устойчивости
Теория колебаний
Механика жидких
сред
Теория ползучести
Теория пластичности
Теория упругости
Механика газовых
сред
Механика
Механика
сплошных сред
7.
РЕАЛЬНЫЙ ОБЪЕКТ И РАСЧЕТНАЯ СХЕМА7
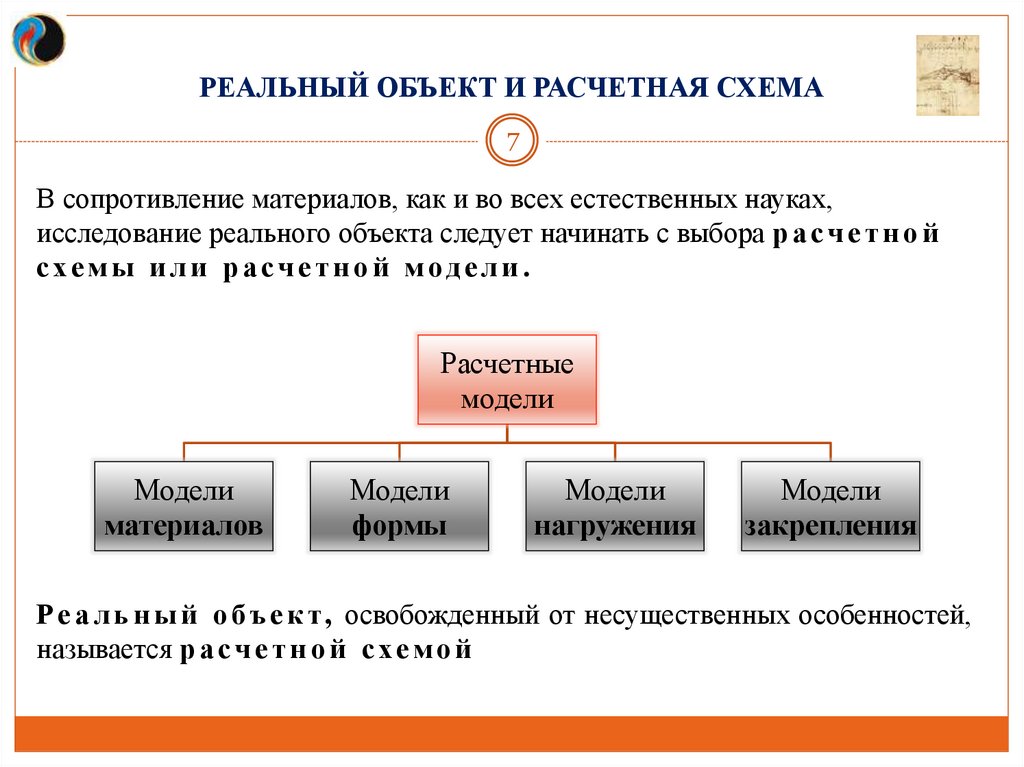
В сопротивление материалов, как и во всех естественных науках,
исследование реального объекта следует начинать с выбора р а с ч е т н о й
схемы или расчетной модели .
Расчетные
модели
Модели
материалов
Модели
формы
Модели
нагружения
Модели
закрепления
Р е а л ь н ы й о б ъ е к т, освобожденный от несущественных особенностей,
называется р а с ч е т н о й с х е м о й
8.
МОДЕЛИ МАТЕРИАЛОВ8
Построение расчетной схемы следует начинать со схематизации структуры и
свойств материала.
Допущения о свойствах материалов
Материал следует считать:
1. Сплошным
Сплошность – понятие, предполагающее, что материал полностью заполняет
занимаемый объем и распределен в нем без пустот и разрывов.
2. Однородным
Однородность – независимость механических характеристик от координат
частиц тела. Материал имеет одинаковые свойства во всех точках
образца.
3. Изотропным
Изотропность означает, что в одной и той же точке тела механические и
физические характеристики материала во всех направлениях одинаковы.
4. Идеально-упругим
Идеальная упругость – свойство полностью восстанавливать форму и размеры
после устранения причин, вызывающих это изменение.
9.
ДОПОЛНИТЕЛЬНЫЕ ГИПОТЕЗЫ СОПРОТИВЛЕНИЯ МАТЕРИАЛОВ9
1. Допущения о деформациях
Деформации подразделяются на:
Упругие деформации обратимы, то есть исчезают после устранения
причин, их вызывающих.
Пластические деформации необратимы, то есть остаются после
устранения причин, их вызвавших.
2. Гипотеза об отсутствии первоначальных внутренних усилий.
3. Принцип неизменности начальных размеров (принцип
отвердения).
4. Гипотеза о линейной деформируемости тел (закон Гука).
5. Гипотеза независимости действия сил (принцип суперпозиции).
6. Гипотеза плоских сечений (гипотеза Бернулли) – сечения,
перпендикулярные оси стержня и плоские до деформации, остаются
плоскими и перпендикулярными оси после деформации.
7. Принцип Сен-Венана – напряженное состояние тела на достаточном
удалении от области действия локальных нагрузок очень мало зависит от
способа их приложения.
10.
МОДЕЛИ ФОРМЫ10
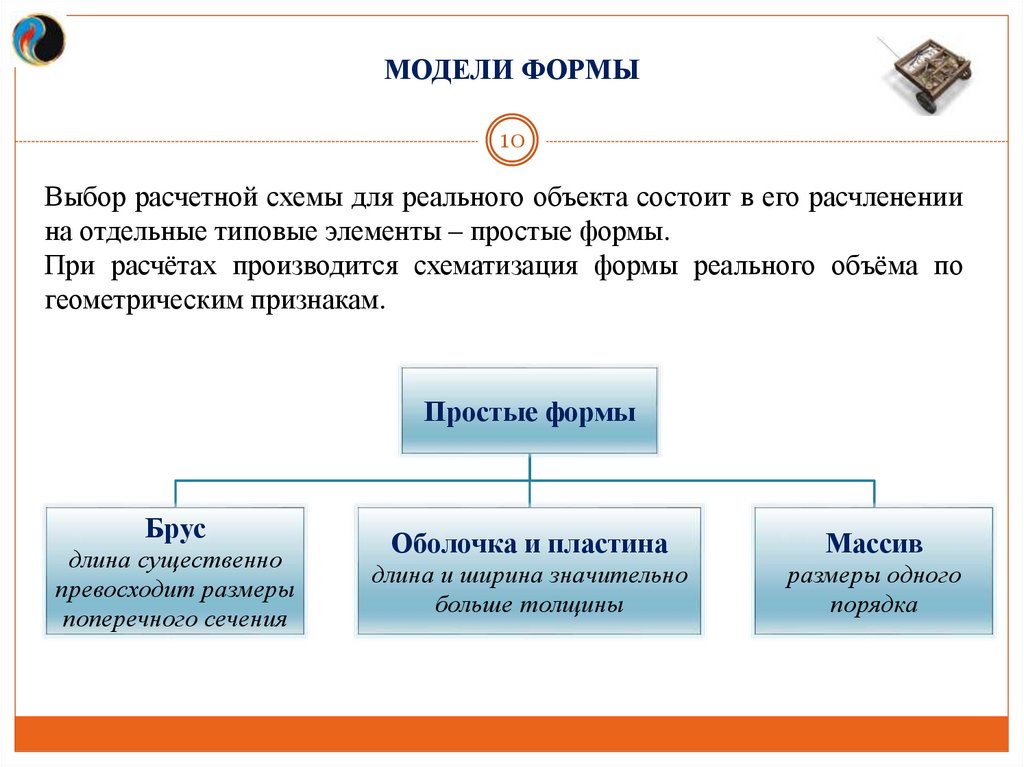
Выбор расчетной схемы для реального объекта состоит в его расчленении
на отдельные типовые элементы – простые формы.
При расчётах производится схематизация формы реального объёма по
геометрическим признакам.
Простые формы
Брус
длина существенно
превосходит размеры
поперечного сечения
Оболочка и пластина
Массив
длина и ширина значительно
больше толщины
размеры одного
порядка
11.
БРУС11
Брус – геометрическое тело, два размера которого намного меньше его
третьего размера.
Брусья бывают прямолинейные, криволинейные, постоянного сечения,
переменного сечения, комбинированные.
d
l
l
l
Балка – брус, работающий на изгиб.
Вал – брус, передающий вращательное движение.
Стержень – брус, работающий на растяжение-сжатие.
12.
ОБОЛОЧКА12
Оболочка – это конструкция, ограниченная двумя криволинейными
поверхностями, расстояние между которыми мало по сравнению с её
другими размерами.
Оболочки бывают тонкостенные и толстостенные.
По форме различают цилиндрические, конические, сферические оболочки.
Примеры: резервуары для хранения нефте-продуктов и газа, трубопроводы,
купола зданий, корпуса машин, самолетов, судов.
13.
ПЛАСТИНА13
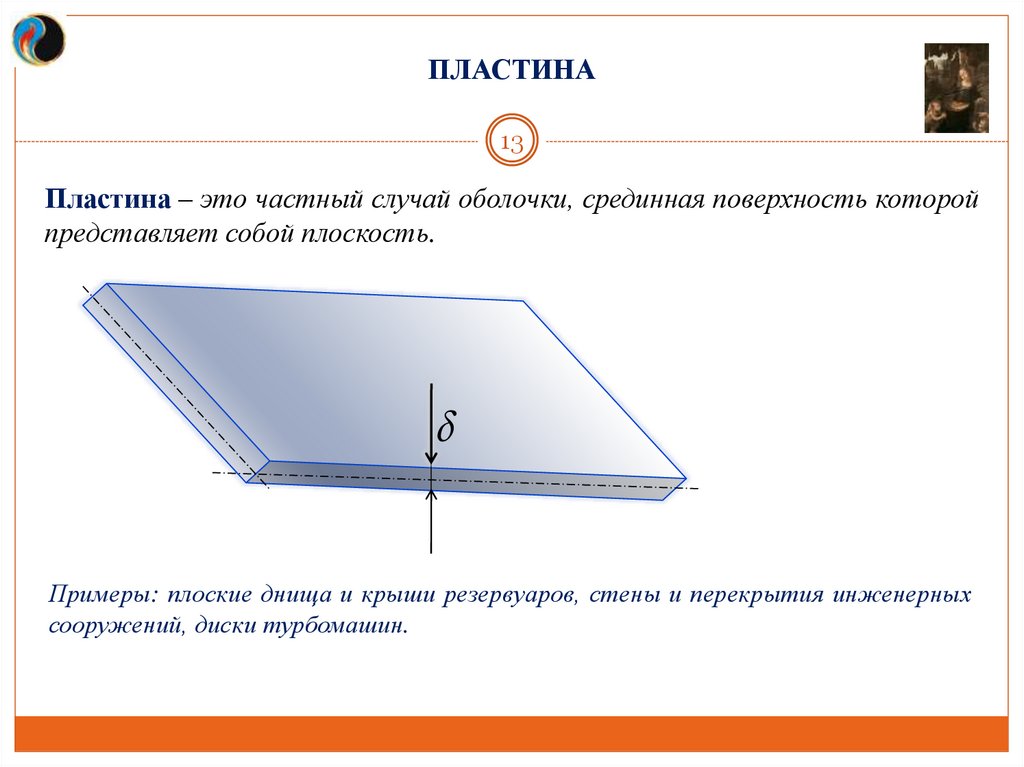
Пластина – это частный случай оболочки, срединная поверхность которой
представляет собой плоскость.
Примеры: плоские днища и крыши резервуаров, стены и перекрытия инженерных
сооружений, диски турбомашин.
14.
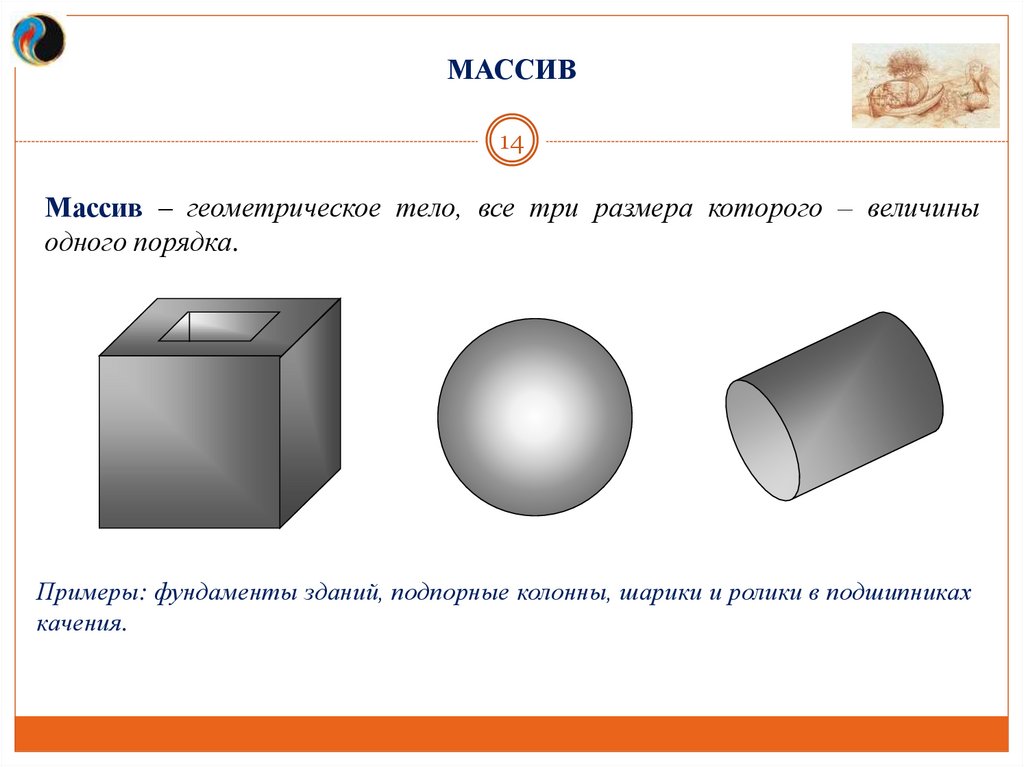
МАССИВ14
Массив – геометрическое тело, все три размера которого – величины
одного порядка.
Примеры: фундаменты зданий, подпорные колонны, шарики и ролики в подшипниках
качения.
15.
МОДЕЛИ НАГРУЖЕНИЯ15
Силы подразделяют на внешние, приложенные
внутренние, возникающие в элементах конструкции.
к
конструкции,
и
Внешние силы – силы, которые обусловлены действием на тело других
тел или внешней среды.
Внутренние силы – усилия или моменты, обусловленные действием
одной части тела на другую внутри какой-либо изолированной системы.
16.
УСЛОВНАЯ КЛАССИФИКАЦИЯ ВНЕШНИХ СИЛ16
- по характеру действия:
• статические;
• динамические (циклические, ударные, внезапно приложенные);
- по характеру приложения:
• сосредоточенные (силы Р [H] и моменты M [H·м]);
=
17.
УСЛОВНАЯ КЛАССИФИКАЦИЯ ВНЕШНИХ СИЛ17
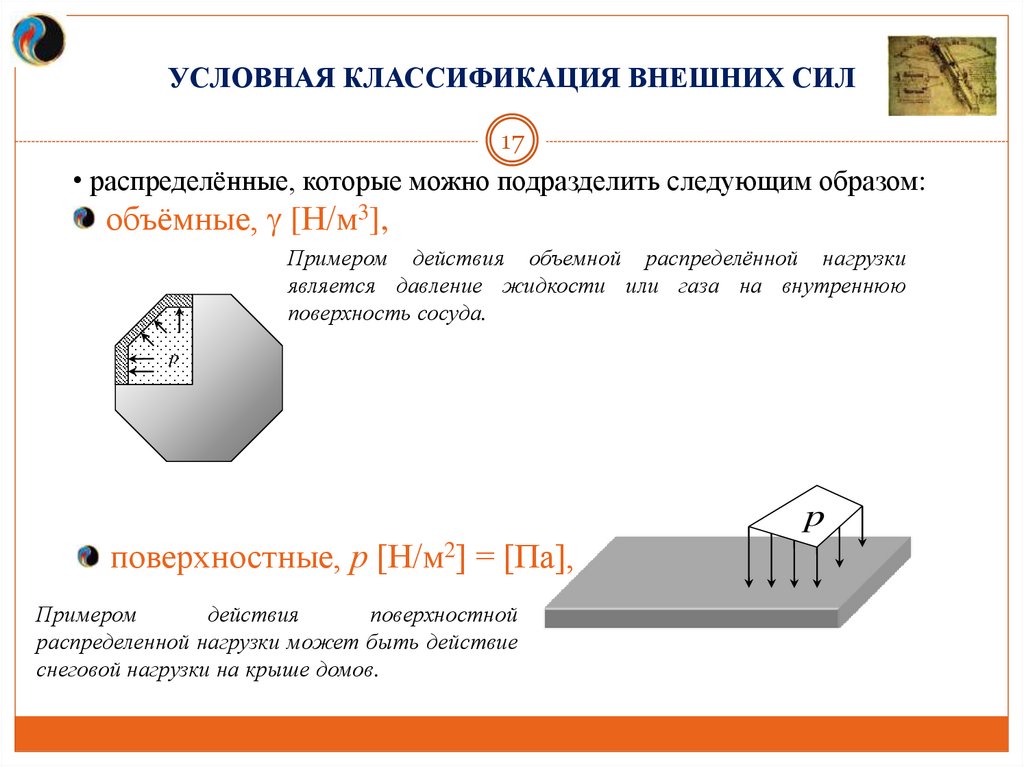
• распределённые, которые можно подразделить следующим образом:
объёмные, [Н/м3],
Примером действия объемной распределённой нагрузки
является давление жидкости или газа на внутреннюю
поверхность сосуда.
p
p
поверхностные, р [Н/м2] = [Па],
Примером
действия
поверхностной
распределенной нагрузки может быть действие
снеговой нагрузки на крыше домов.
18.
УСЛОВНАЯ КЛАССИФИКАЦИЯ ВНЕШНИХ СИЛ18
линейные, q [Н/м]; Примером действия линейной распределенной нагрузки
может быть нагрузка на балочные перекрытия.
y
P
ᾨ
b
q z P q z dz
z
a
b
- по возникновению:
• активные (силы P [H] и моменты M [H м])
• реактивные (реакции опор).
a
площадь фигуры, ограничивающей
влияние распределённой нагрузки.
19.
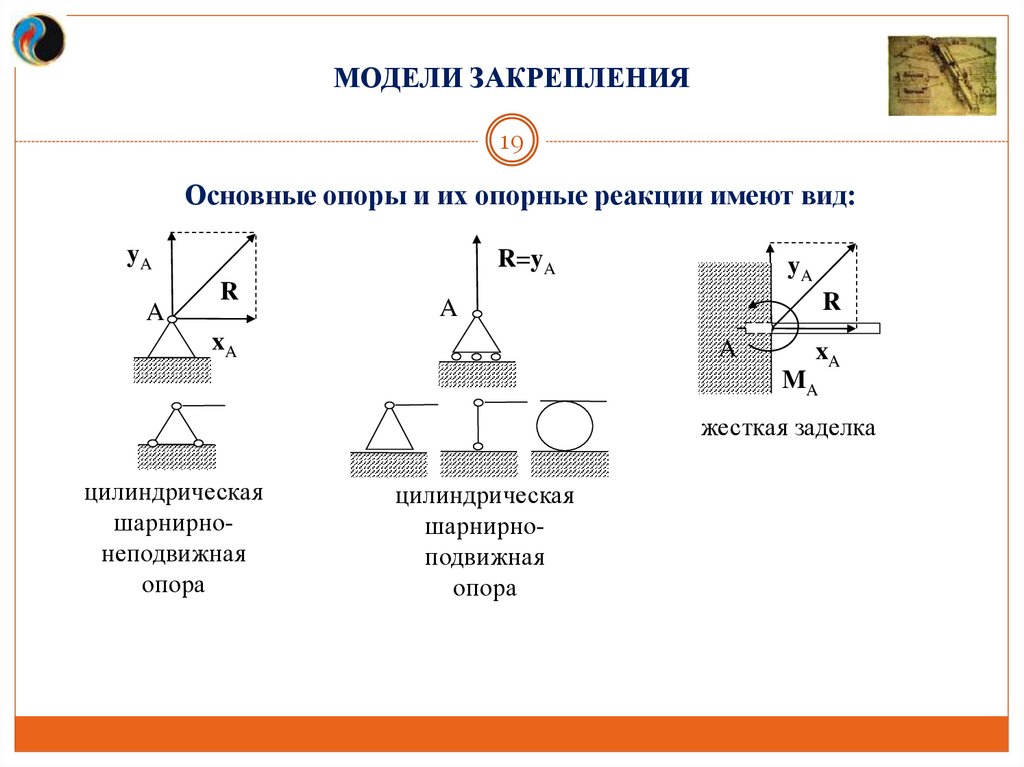
МОДЕЛИ ЗАКРЕПЛЕНИЯ19
Основные опоры и их опорные реакции имеют вид:
yA
A
R=yA
R
yA
R
A
xA
A
xA
MA
жесткая заделка
цилиндрическая
шарнирнонеподвижная
опора
цилиндрическая
шарнирноподвижная
опора
20.
ОПРЕДЕЛЕНИЕ ВНУТРЕННИХ СИЛОВЫХ ФАКТОРОВМЕТОД СЕЧЕНИЙ
20
Для проведения расчетов на прочность необходимо знать внутренние усилия, которые
определяются с помощью метода сечений.
РАЗРЕЗАЕМ БРУС ПЛОСКОСТЬЮ, ПЕРПЕНДИКУЛЯРНОЙ ЕГО ОСИ
P2
Pn
левая половина
I
правая половина
S
P2
Pi
II
P3
плоскость,
оси бруса
перпендикулярная
P4
21.
ОПРЕДЕЛЕНИЕ ВНУТРЕННИХ СИЛОВЫХ ФАКТОРОВМЕТОД СЕЧЕНИЙ
21
ОТБРАСЫВАЕМ ТУ ЧАСТЬ БРУСА, КОТОРАЯ СОДЕРЖИТ БОЛЬШЕЕ
КОЛИЧЕСТВО НЕИЗВЕСТНЫХ
P1
P2
P3
A
PA
Pn
A
PA
Pi
P4
22.
ОПРЕДЕЛЕНИЕ ВНУТРЕННИХ СИЛОВЫХ ФАКТОРОВМЕТОД СЕЧЕНИЙ
22
ЗАМЕНЯЕМ ДЕЙСТВИЕ ОТБРОШЕННОЙ ЧАСТИ РАВНОДЕЙСТВУЮЩИМИ
УСИЛИЯМИ
R Главный вектор системы внутренних сил;
My
y
Qy
Qx
x
Mx
R
M
z
y
Mz
M
Главный момент системы внутренних сил;
N
Нормальная (продольная) сила;
Qx , Q y
Mz
Поперечные силы;
Крутящий момент;
Mx,M y
Изгибающие моменты
Перечисленные силы и моменты являются внутренними силовыми факторами
23.
ОПРЕДЕЛЕНИЕ ВНУТРЕННИХ СИЛОВЫХ ФАКТОРОВМЕТОД СЕЧЕНИЙ
23
СОСТАВЛЯЕМ УРАВНЕНИЯ РАВНОВЕСИЯ ДЛЯ ОПРЕДЕЛЕНИЯ ВНУТРЕННИХ
СИЛОВЫХ ФАКТОРОВ (СИЛ И МОМЕНТОВ):
n
N Piz 0;
i 1
n
n
Qx Pix 0;
i 1
n
Q y Piy 0;
i 1
n
n
M k m0z Pi 0; M x m0x Pi 0; M y m0y Pi 0.
i 1
i 1
i 1
24.
НАПРЯЖЕНИЯ, ПЕРЕМЕЩЕНИЯ, ДЕФОРМАЦИИ24
Напряжением называется интенсивность внутренней силы в данной точке
поперечного сечения.
у
Размерность напряжения:
dR
dQy
p Н2 Па
м
dF
dQx
dN
х
z
Полным напряжением в точке называется векторная величина:
dR
dF 0 dF
p lim
где:
dR - равнодействующая сил;
dF - элемент площади поперечного сечения.
25.
НАПРЯЖЕНИЕ25
Разложим полное напряжение на нормальное напряжение и
касательные напряжения
Полное напряжение в точке определяется по формуле:
p
2
z
2
zx
2
zy
26.
ЗАВИСИМОСТИ МЕЖДУ НАПРЯЖЕНИЯМИ И ВНУТРЕННИМИСИЛОВЫМИ ФАКТОРАМИ
26
N dF M z ( y zx x zy )dF dF
F
F
Qx zx dF M y x z dF
F
F
Где:
ρ – полярный радиус (кратчайшее
расстояние от точки приложения
силы до центра тяжести
сечения).
dQ
τ - полное касательное
напряжение
dF
F
Q y zy dF M x y z dF
F
F
x2 y 2
2
dQy dQx
2
2
zy zx
dF dF
2
27.
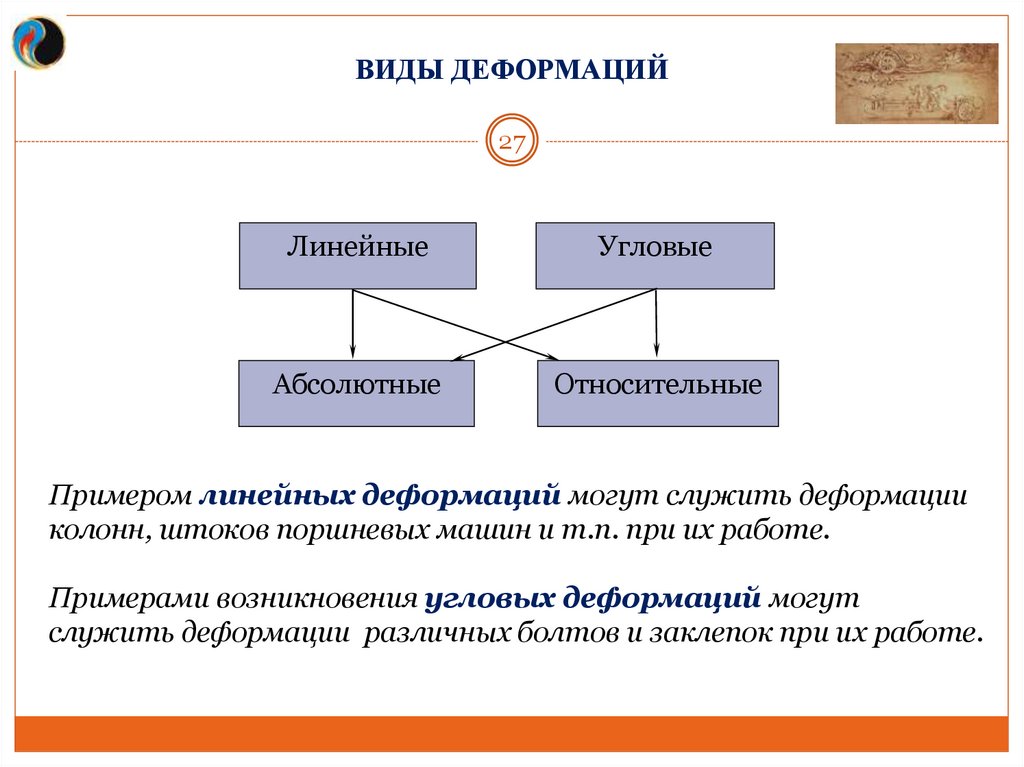
ВИДЫ ДЕФОРМАЦИЙ27
Линейные
Угловые
Абсолютные
Относительные
Примером линейных деформаций могут служить деформации
колонн, штоков поршневых машин и т.п. при их работе.
Примерами возникновения угловых деформаций могут
служить деформации различных болтов и заклепок при их работе.
28.
ЛИНЕЙНЫЕ ДЕФОРМАЦИИ28
A
B
деформация
A
B
Абсолютной линейной деформацией l
называется разность между конечной lк
и начальной длиной lн отрезка AB :
=
l lк lн
А В АВ
Относительной линейной деформацией в
точке А по направлению называется безразмерная
величина, равная:
A' B' AB
ε AB lim
AB 0
AB
29.
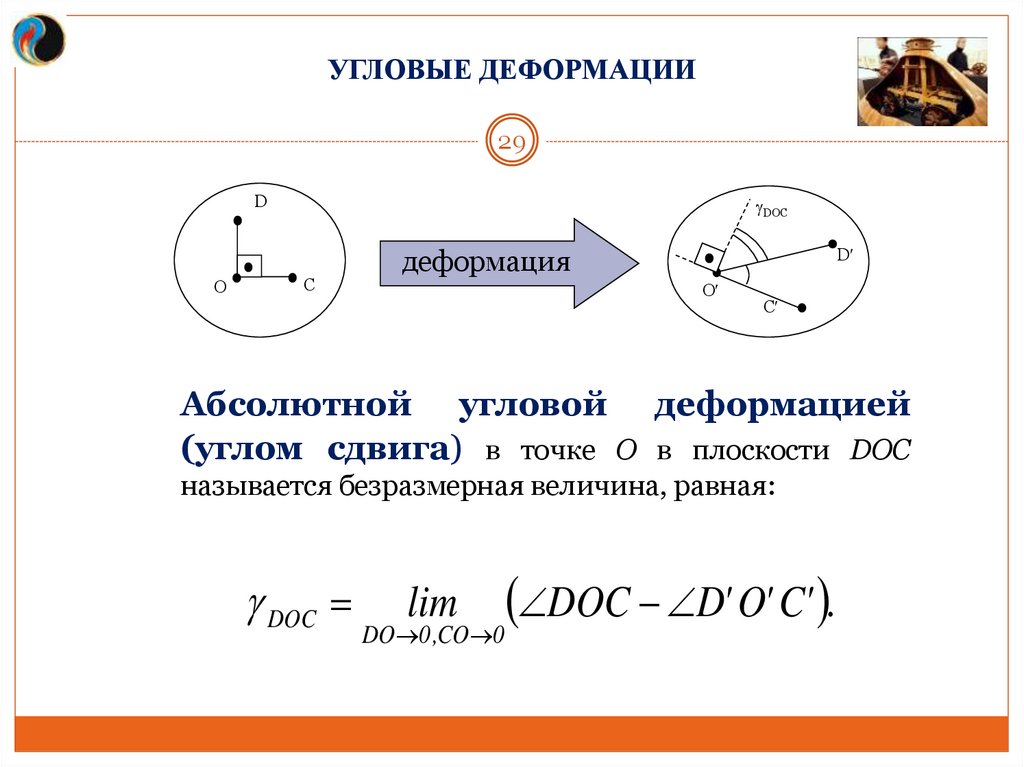
УГЛОВЫЕ ДЕФОРМАЦИИ29
D
O
DOC
C
деформация
D
O
C
Абсолютной угловой деформацией
(углом сдвига) в точке О в плоскости DOC
называется безразмерная величина, равная:
DOC
DOC D' O' C' .
DO 0 ,CO 0
lim
30.
УГЛОВЫЕ ДЕФОРМАЦИИS
a P
30
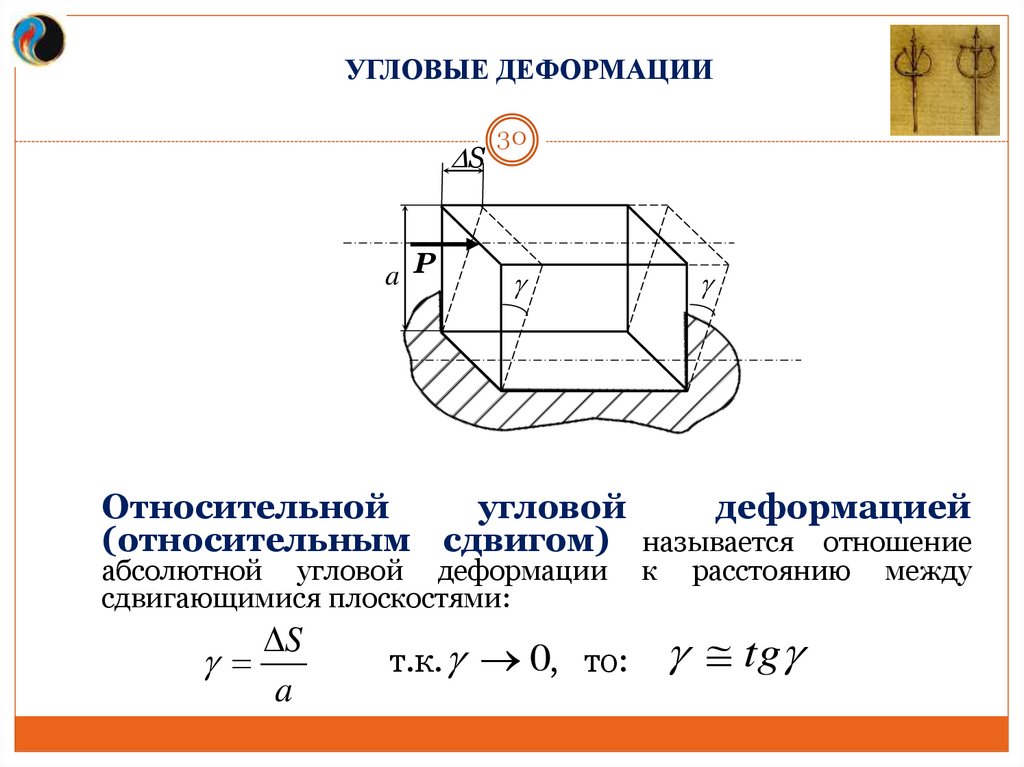
Относительной
угловой
деформацией
(относительным сдвигом) называется отношение
абсолютной угловой деформации
сдвигающимися плоскостями:
S
a
т.к. 0, то:
к
расстоянию
tg
между
31.
НАПРЯЖЕНИЯ, ПЕРЕМЕЩЕНИЯ, ДЕФОРМАЦИИ31
Совокупность напряжений для множества площадок, проходящих через
данную точку, образуют напряжённое состояние в точке.
Совокупность линейных и угловых деформаций по различным направлениям и
плоскостям для одной точки определяют деформированное состояние в
точке.
Деформированное состояние точки тела полностью определяется 6-ю
компонентами деформации:
Линейные ( εx; εy; εz )
Угловые ( γxy; γyz; γxz )
Перемещения являются абсолютными величинами, выражаемыми в
единицах длины или в радианах (Δl, f, , ).
Деформации являются относительными величинами, выражаемыми в
процентах, или безразмерными:
l l
к н 100%
lн
l
l





















 Механика
Механика








