Представление информации в ЭВМ

1.

2.

В важные эпохи жизни
иногда в самом обыкновенном
человеке разгорается искра
геройства, неизвестно доселе
тлевшая в груди его, и тогда
он совершает дела, о коих до
сих пор ему не случалось и
грезить, которым даже после
он сам едва верует.
Михаи́л Ю́рьевич
Ле́рмонтов (1814 - 1841) русский поэт, прозаик, драматург,
художник.
Михаил Лермонтов

3.  

Лекция 2
по дисциплине
«Организация ЭВМ и систем»
Тема:
Представление информации в
вычислительных машинах. Логические
основы построения ЭВМ
Демонстрируется видеоролик
«Двоичная система счисления» – 2 мин. 40 с.

4.

5. 1. Система счисления

6.

Информация в компьютере кодируется в двоичной,
восьмиричной, шестнадцатиричной или в двоичнодесятичной системах счисления.
Система счисления — способ именования и
изображения чисел с помощью символов, имеющих
определенные количественные значения.
В зависимости от способа изображения чисел,
системы счисления делятся:
• на позиционные;
• непозиционные.
В позиционной системе счисления количественное
значение каждой цифры зависит от ее места (позиции)
в числе.

7. Количество различных цифр (Р), используемых для изображения числа в позиционной системе счисления, называется основанием

системы счисления.
В общем случае запись любого смешанного числа
в системе счисления с основанием Р будет
представлять собой ряд вида
N = am-1Pm-1 + am-2Pm-2 + … + akPk + … + a0P0 + a-1P-1 + a-2P-2 + a-sP-s
Нижние индексы определяют местоположение цифры в числе:
- для целой части m-разрядов имеют положительные значения;
- для дробной части s-разрядов имеют отрицательные значения.

8. Максимальное целое число, которое может быть представлено в т разрядах, Минимальное значащее, не равное 0 число, которое можно

записать в s разрядах дробной части,
Имея в целой части числа т, а в дробной — s
разрядов, можно записать всего Pm+S разных чисел.

9. Максимальное целое число, которое может быть представлено в т разрядах, Минимальное значащее, не равное 0 число, которое можно

записать в s разрядах дробной части,
Имея в целой части числа т, а в дробной — s
разрядов, можно записать всего Pm+S разных чисел.

10. Представление числа 136046.625 в десятичной системе счисления

N = am-1Pm-1 + am-2Pm-2 + … + akPk + … + a0P0 + a-1P-1 + a-2P-2 + a-sP-s

11. Представление числа 46.625 в двоичной системе счисления

N = am-1Pm-1 + am-2Pm-2 + … + akPk + … + a0P0 + a-1P-1 + a-2P-2 + a-sP-s

12. Представление числа 46.625 в восьмиричной системе счисления

N = am-1Pm-1 + am-2Pm-2 + … + akPk + … + a0P0 + a-1P-1 + a-2P-2 + a-sP-s

13. Представление числа 46.625 в шестнадцатиричной системе счисления

N = am-1Pm-1 + am-2Pm-2 + … + akPk + … + a0P0 + a-1P-1 + a-2P-2 + a-sP-s

14.

Итоговая запись числа в общем виде и различных
системах счисления имеют вид:
N = am-1Pm-1 + am-2Pm-2 + … + akPk + … + a0P0 + a-1P-1 + a-2P-2 + a-sP-s
N(дес) = 100000·1 + 10000·3 + 1000·6 + 100·0 + 10·4 + 1·6 + 0.1·6 + 0.01·2
+ 0.001·5 = 136046.625
N(дв) = 32·1 + 16·0 + 8·1 + 4·1 + 2·1 + 1·0 + 0.5·1 + 0.25·0 + 0.125·1 =
46.625
N(в) = 8·5 + 1·6 + 0.125·5 = 46.625
N(ш) = 16·2 + 1·e + 0.01625·a = 46.625

15.

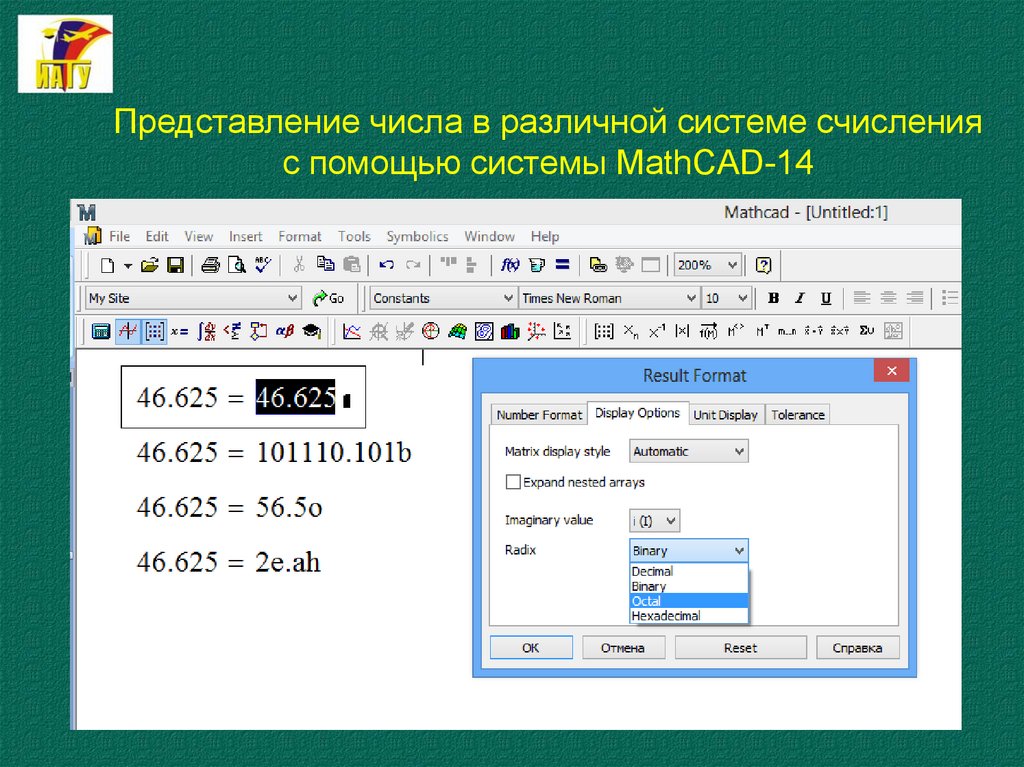
Представление числа в различной системе счисления с
помощью системы MathCAD-14

16.

Представление числа в различной системе счисления
с помощью системы MathCAD-14

17. В вычислительных машинах применяются две формы представления двоичных чисел: - естественная форма, или форма с фиксированной

запятой ;
- нормальная форма, или форма с плавающей запятой.
Знак числа обычно кодируется двоичной цифрой,
при этом код 0 означает знак (плюс), код 1 — знак (минус).

18. 2. Выполнение арифметических операций в компьютере

19. Правила выполнения арифметических операций в двоичной системе счисления аналогичны правилам выполнения операций в десятичной

системе
счисления. Например:

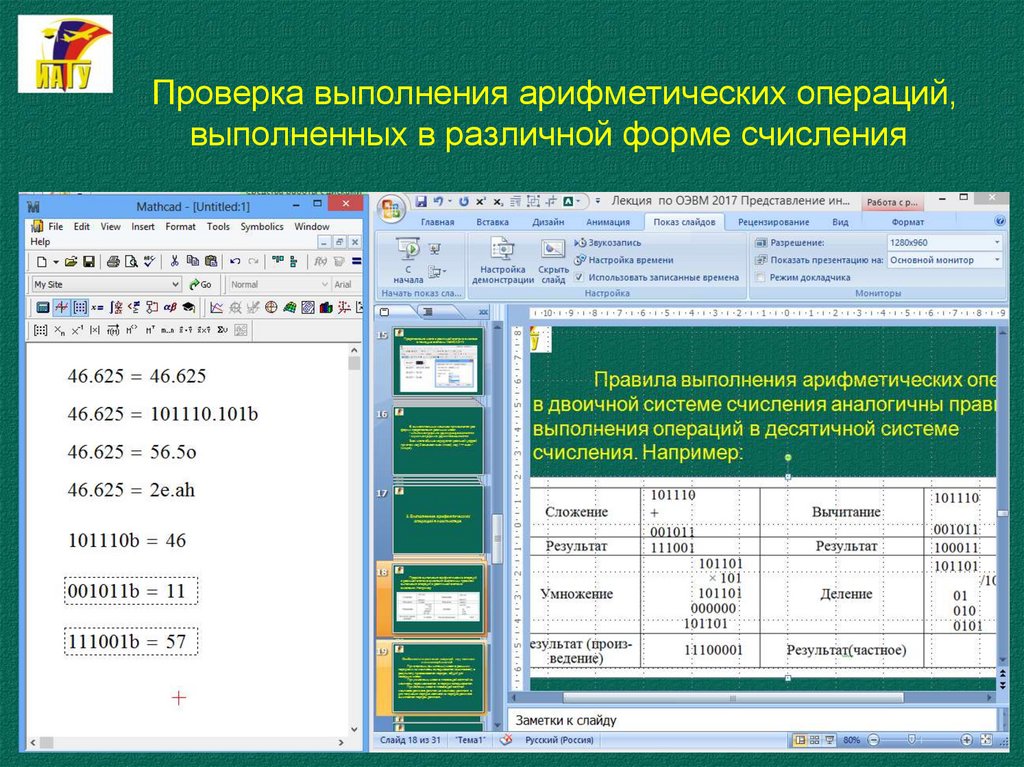
20.

Проверка выполнения арифметических операций,
выполненных в различной форме счисления

21. Особенности выполнения операций над числами с плавающей запятой При сложении (вычитании) чисел с разными порядками их мантиссы

складываются (вычитаются), а
результату присваивается порядок, общий для
исходных чисел.
При умножении чисел с плавающей запятой их
мантиссы перемножаются, а порядки складываются.
При делении чисел с плавающей запятой
мантисса делимого делится на мантиссу делителя, а
для получения порядка частного из порядка делимого
вычитается порядок делителя.

22. 3. Элементы алгебры логики

23.

Алгебра логики — это раздел математической
логики, значения всех элементов (функций и
аргументов) которой определены в двухэлементном
множестве: 0 и 1.
Алгебра логики оперирует с логическими
высказываниями.

24. Высказывание — это любое предложение, в отношении которого имеет смысл утверждение о его истинности или ложности. При этом

считается, что
высказывание удовлетворяет закону исключенного
третьего, то есть каждое высказывание или истинно,
или ложно, и не может быть одновременно и истинным
и ложным.
Высказывания:
- «Сейчас идет снег» — это утверждение может быть истинным
или ложным;
- «Москва — столица России» — истинное утверждение;
- «Частное от деления 10 на 2 равно 3» — ложное утверждение.

25. В алгебре логики все высказывания обозначают буквами a, b, c и т. д. В дальнейшем над ними можно производить любые действия,

предусмотренные
алгеброй логики (алгебра Буля).
Простейшими операциями в алгебре логики являются операции
логического сложения (иначе — операция ИЛИ (OR), операция дизъюнкции
(функция Шеффера)) и логического умножения (иначе — операция И (AND),
операция конъюнкции (функция Пирса)).
Для обозначения операции логического сложения
используют символ + или ˅, а логического умножения —
символ · или ˄.
Правила выполнения операций в алгебре логики определяются
рядом аксиом, теорем и следствий. В частности, для алгебры логики
применимы следующие законы:

26.

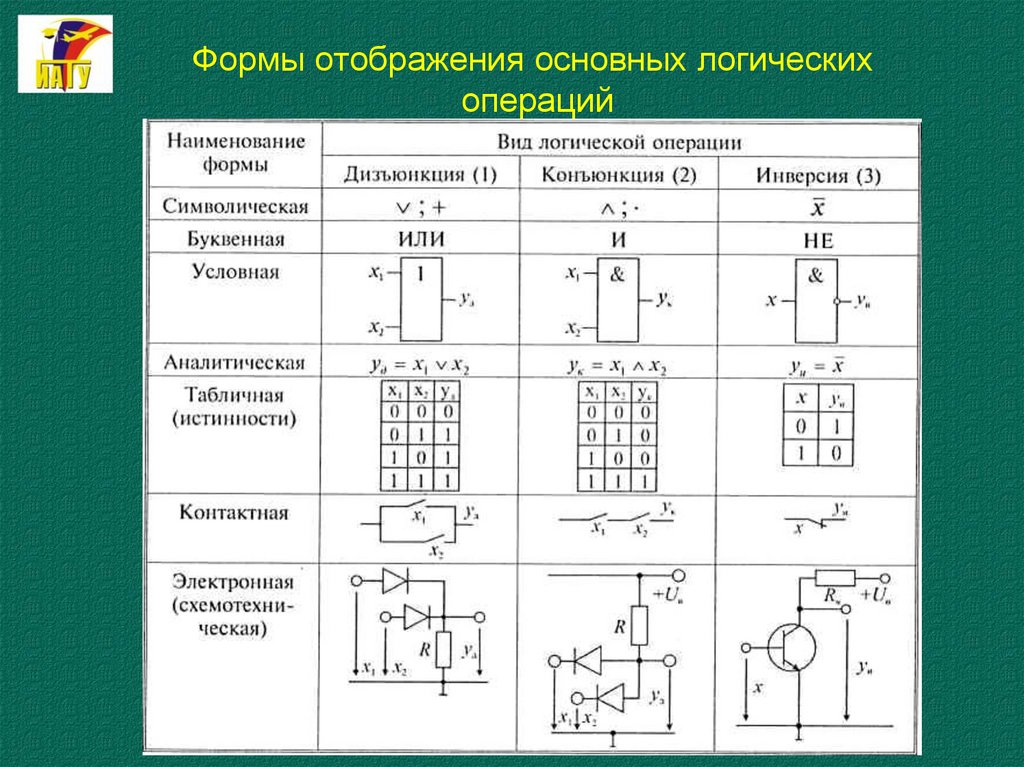
27. Формы отображения основных логических операций

28.

Микросхема К155ЛЛ1 представляет собой четыре
логических элемента 2ИЛИ. Корпус типа 201.14-1,
масса не более 1 г.

29. Формы отображения основных логических операций

O
O

30. Внешний вид и цоколевка микросхемы К155ЛА3

Микросхема К155ЛА3 представляет собой четыре логических элемента 2И-НЕ.
Корпус К155ЛЛ1 типа 201.14-1, масса не более 1

31.

4. Особенности представления
информации в ПК

32.

Числовая информация внутри ПК кодируется в
двоичной, восьмиричной , шестнадцатиричной или в
двоично-десятичной системах счисления.
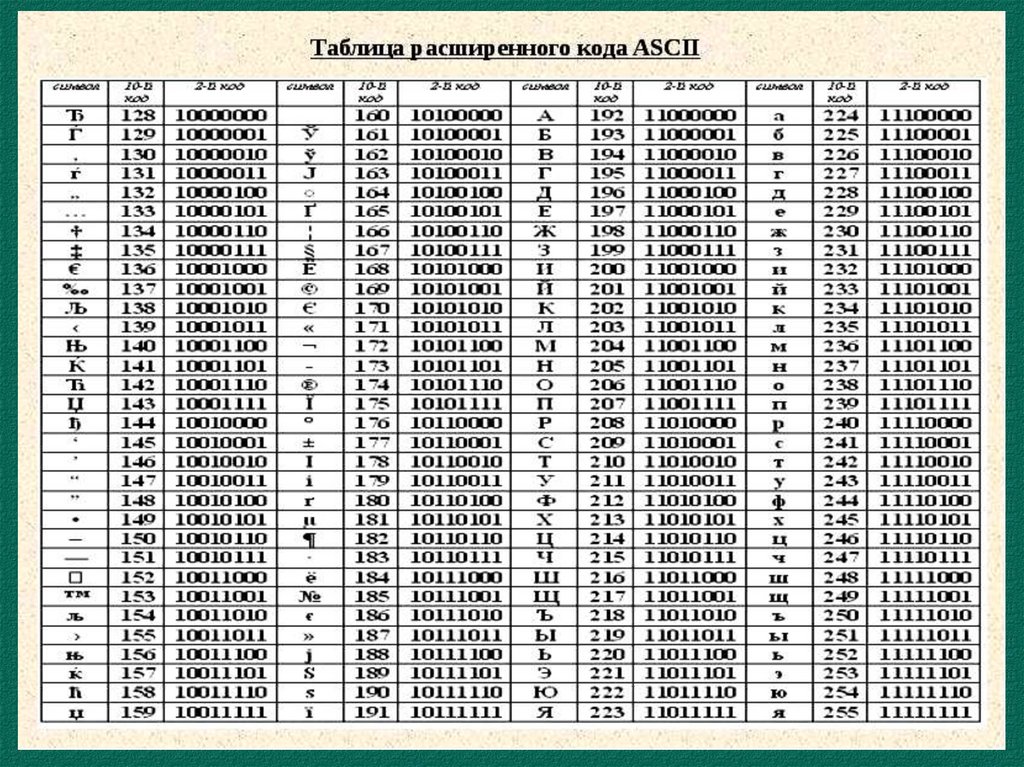
При вводе и выводе любой информации используются специальные шестнадцатиричные коды представления информации — коды ASCII. Эти же коды
применяются для кодирования буквенной и символьной информации и внутри ПК.

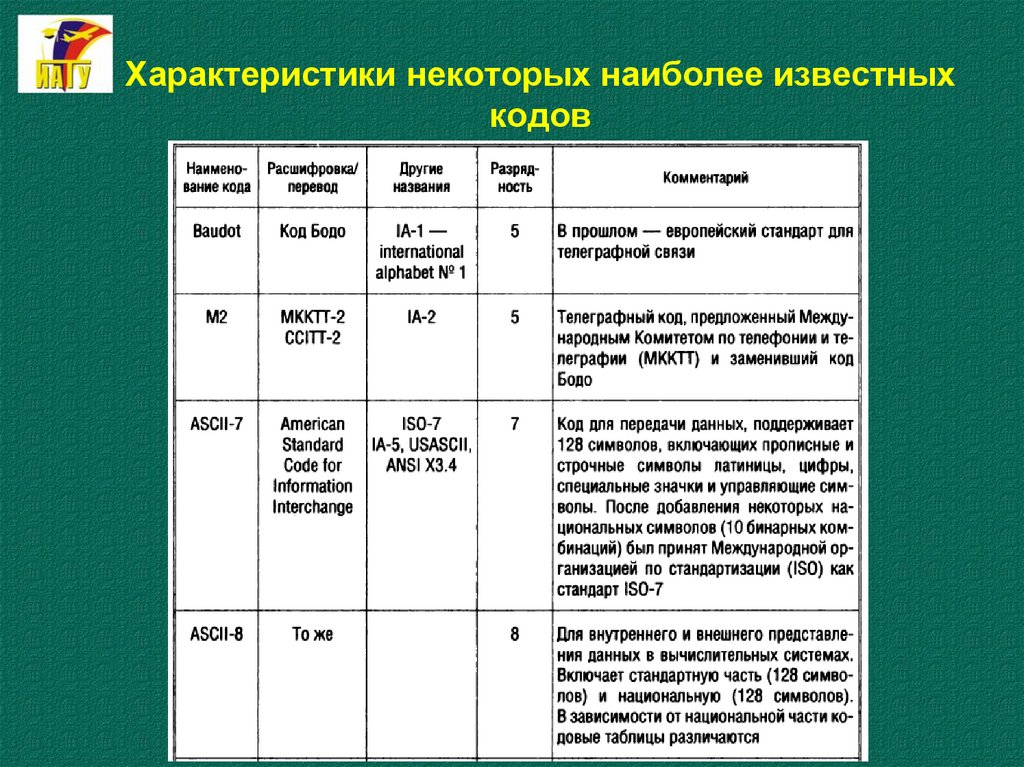
33. Характеристики некоторых наиболее известных кодов

34.

35.

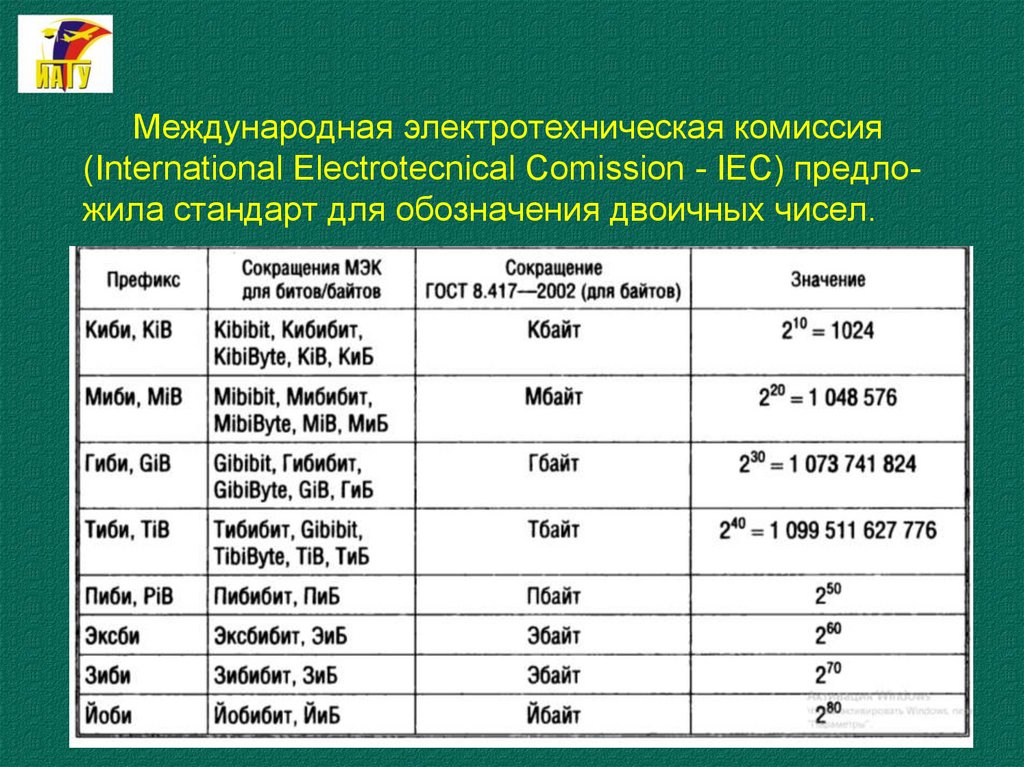
Международная электротехническая комиссия
(International Electrotecnical Comission - IEC) предложила стандарт для обозначения двоичных чисел.

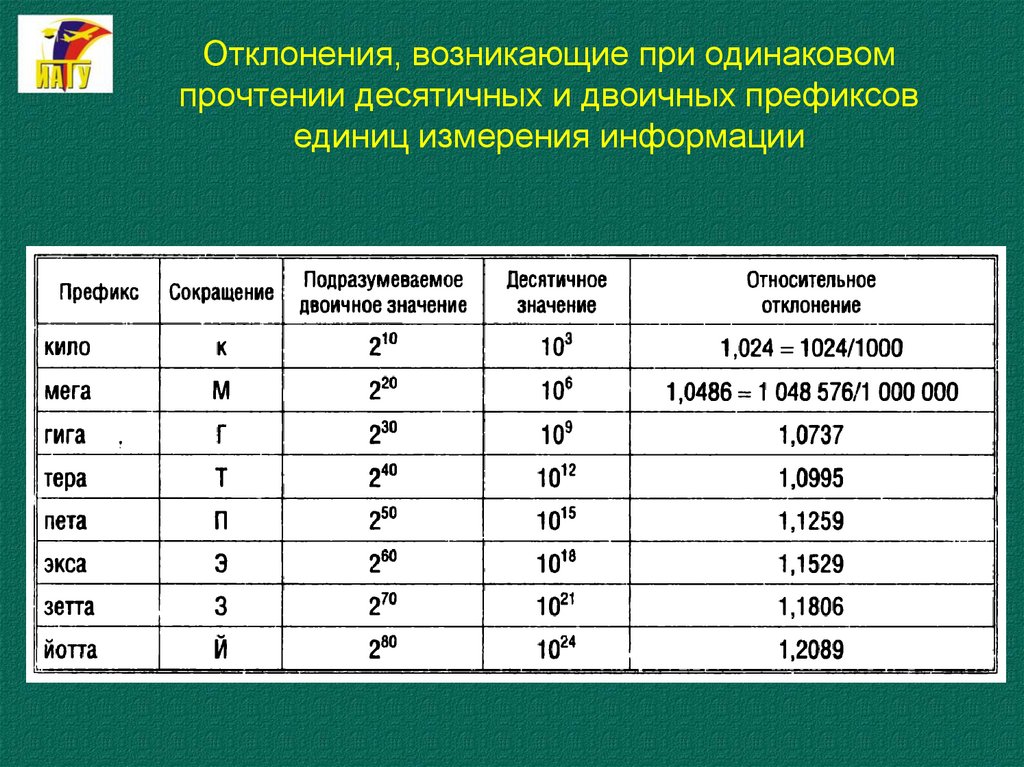
36. Отклонения, возникающие при одинаковом прочтении десятичных и двоичных префиксов единиц измерения информации

37.

Биты в числе нумеруются справа налево,
начиная с 0-го разряда. В ПК могут обрабатываться
поля постоянной и переменной длины.
Поля постоянной длины для ПК :
- полуслово — 1 байт;
- слово — 2 байта;
- двойное слово — 4 байта;
- расширенное слово — 8 байт.
Числа с фиксированной запятой чаще всего имеют
формат слова и полуслова; числа с плавающей запятой
— формат двойного и расширенного слова.

38.

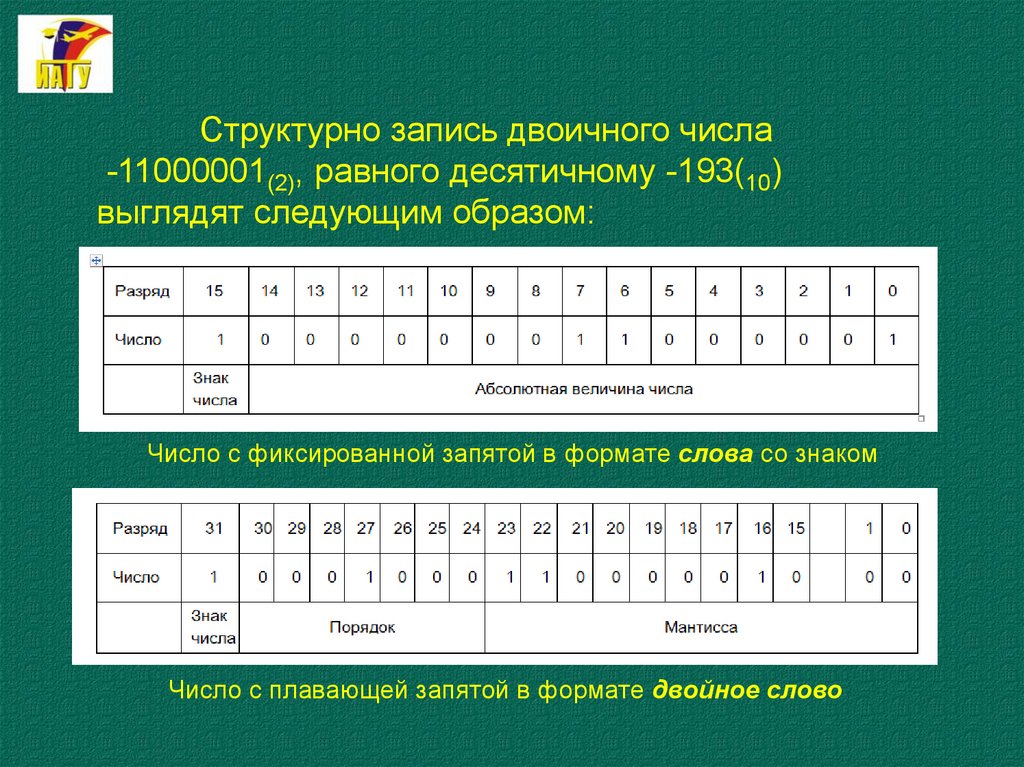
Структурно запись двоичного числа
-11000001(2), равного десятичному -193(10)
выглядят следующим образом:
Число с фиксированной запятой в формате слова со знаком
Число с плавающей запятой в формате двойное слово

39. 5. Логический синтез вычислительных схем

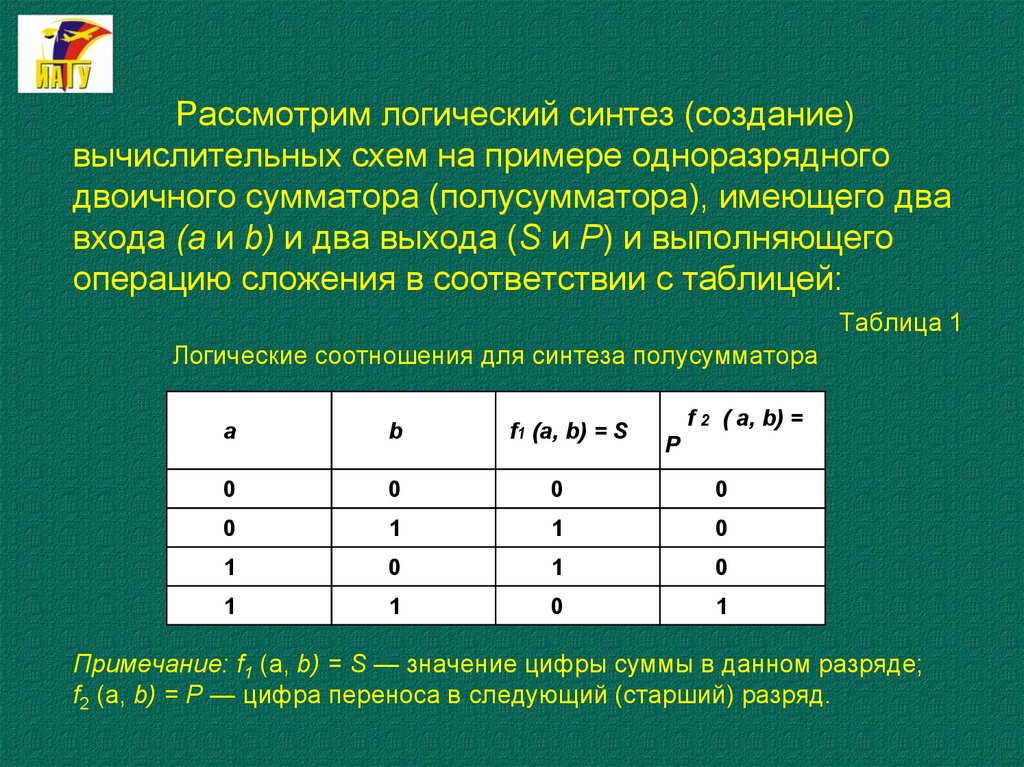
40. Рассмотрим логический синтез (создание) вычислительных схем на примере одноразрядного двоичного сумматора (полусумматора),

имеющего два
входа (а и b) и два выхода (S и Р) и выполняющего
операцию сложения в соответствии с таблицей:
Таблица 1
Логические соотношения для синтеза полусумматора
f 2 ( а, b) =
a
b
f1 (a, b) = S
0
0
0
0
0
1
1
0
1
0
1
0
1
1
0
1
Р
Примечание: f1 (a, b) = S — значение цифры суммы в данном разряде;
f2 (а, b) = Р — цифра переноса в следующий (старший) разряд.

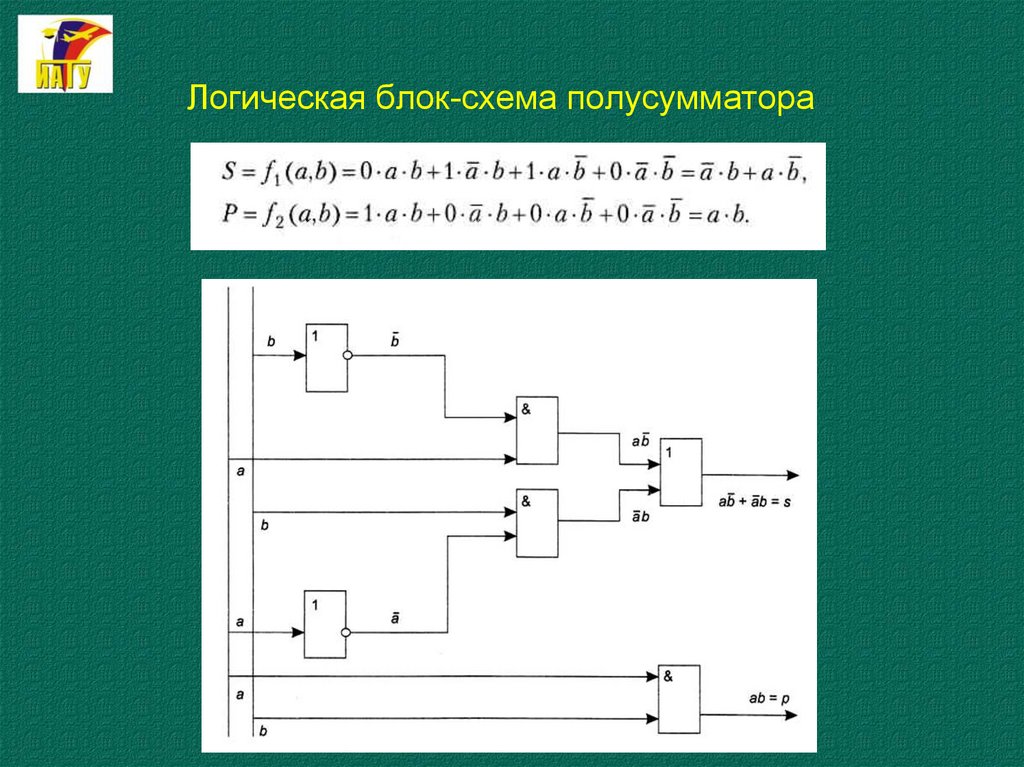
41.

Согласно таблицы можно записать
a
b
f1 (a, b) = S
f 2 ( а, b) = Р
0
0
0
0
0
1
1
0
1
0
1
0
1
1
0
1