Похожие презентации:
XXIV Всероссийская олимпиада школьников по астрономии
1.
Министерство образования и науки Российской ФедерацииАкадемия повышения квалификации и профессиональной
переподготовки работников образования
XXIV Всероссийская олимпиада школьников
по астрономии
Заключительный этап
г. Смоленск, 20-26 марта 2017 г.
Практический тур
2.
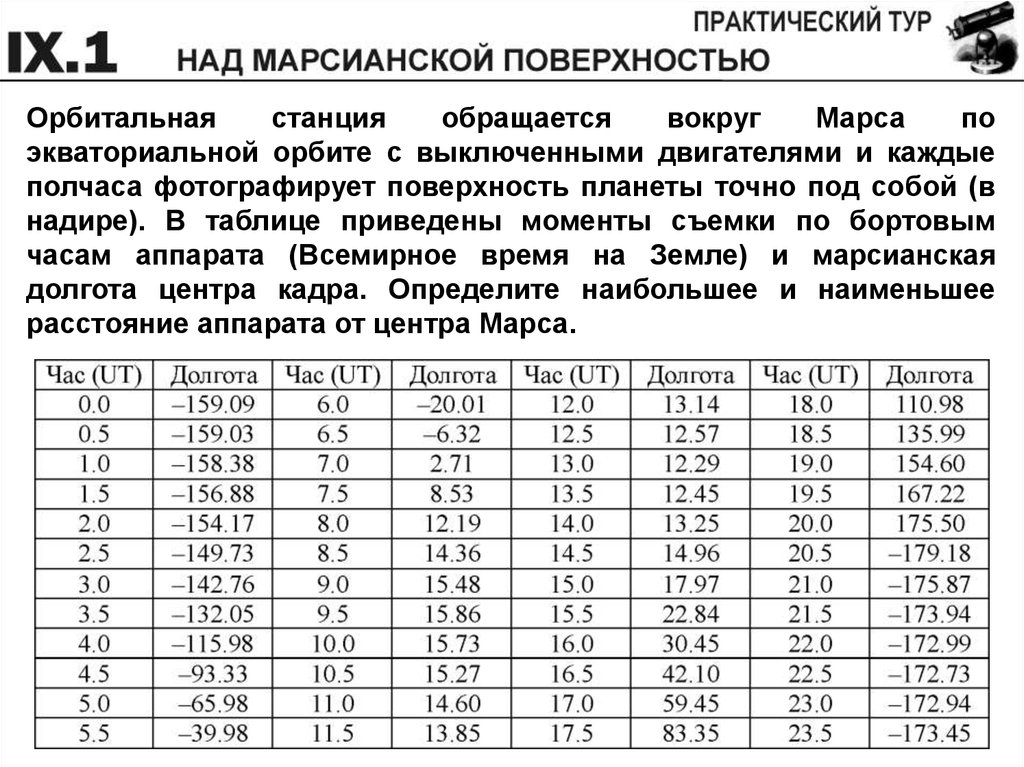
Орбитальнаястанция
обращается
вокруг
Марса
по
экваториальной орбите с выключенными двигателями и каждые
полчаса фотографирует поверхность планеты точно под собой (в
надире). В таблице приведены моменты съемки по бортовым
часам аппарата (Всемирное время на Земле) и марсианская
долгота центра кадра. Определите наибольшее и наименьшее
расстояние аппарата от центра Марса.
3.
Минимальное время облета Марса:На каждом интервале аппарат совершал малую часть оборота.
4.
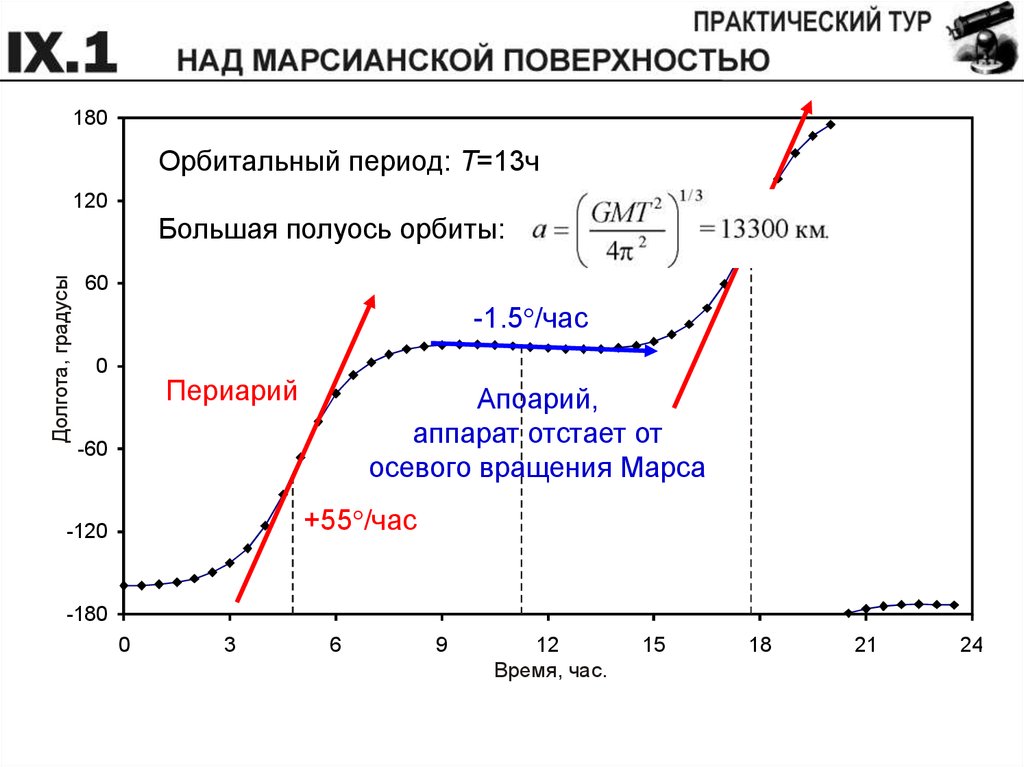
180Орбитальный период: T=13ч
120
Долгота, градусы
Большая полуось орбиты:
60
-1.5 /час
0
Периарий
Апоарий,
аппарат отстает от
осевого вращения Марса
-60
+55 /час
-120
-180
0
3
6
9
12
Время, час.
15
18
21
24
5.
Осевое вращение Марса: S=24.623 ч.Угловые скорости аппарата в периарии и апоарии:
II закон Кеплера:
e = 0.4.
Искомые расстояния:
dMIN = a (1–e) ~8.0 тыс.км; dMAX = a (1+e) ~18.6 тыс.км.
6.
Система оценивания:Интервал существенно короче орб.периода
Орбитальный период
Большая полуось
Соотношение угловых скоростей
2
4
2
8
(либо одной угловой скорости и периода)
Эксцентриситет
Максимальное и минимальное расстояния
4
4
ИТОГО
24
Нет учета вращения Марса
8
7.
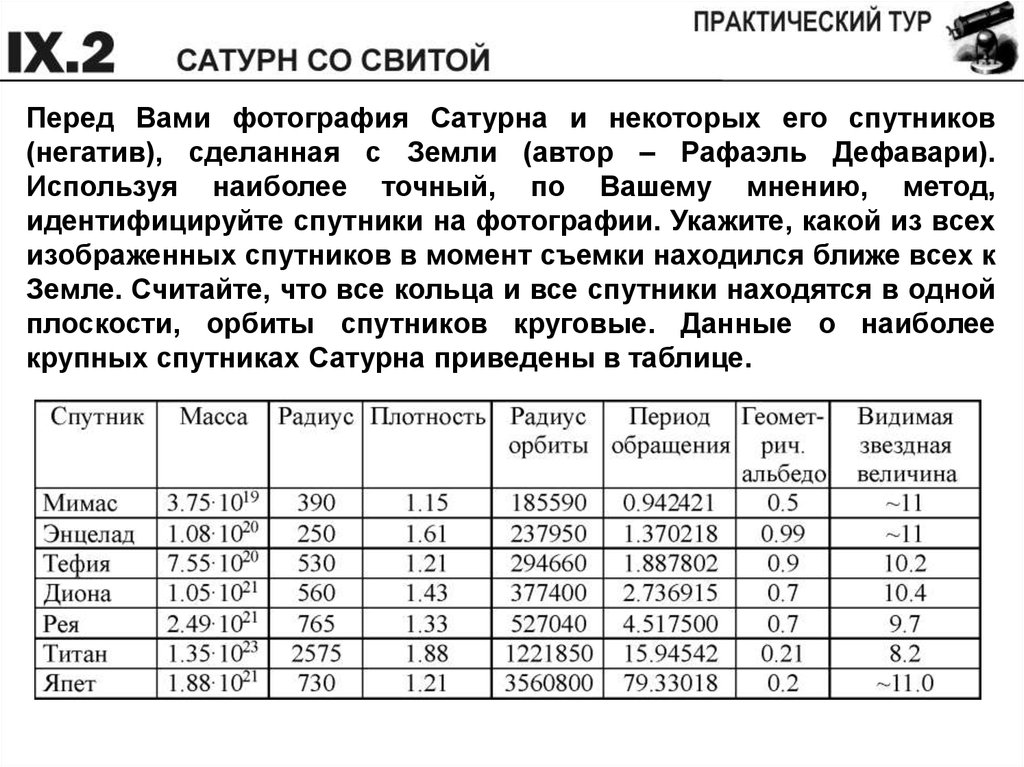
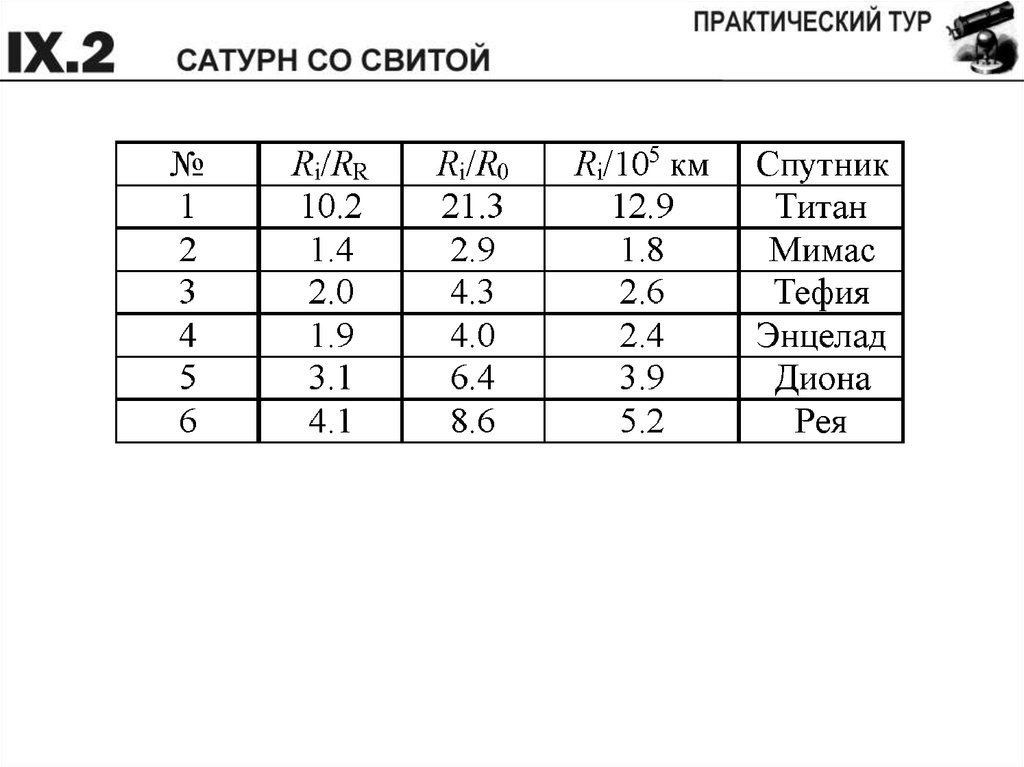
Перед Вами фотография Сатурна и некоторых его спутников(негатив), сделанная с Земли (автор – Рафаэль Дефавари).
Используя наиболее точный, по Вашему мнению, метод,
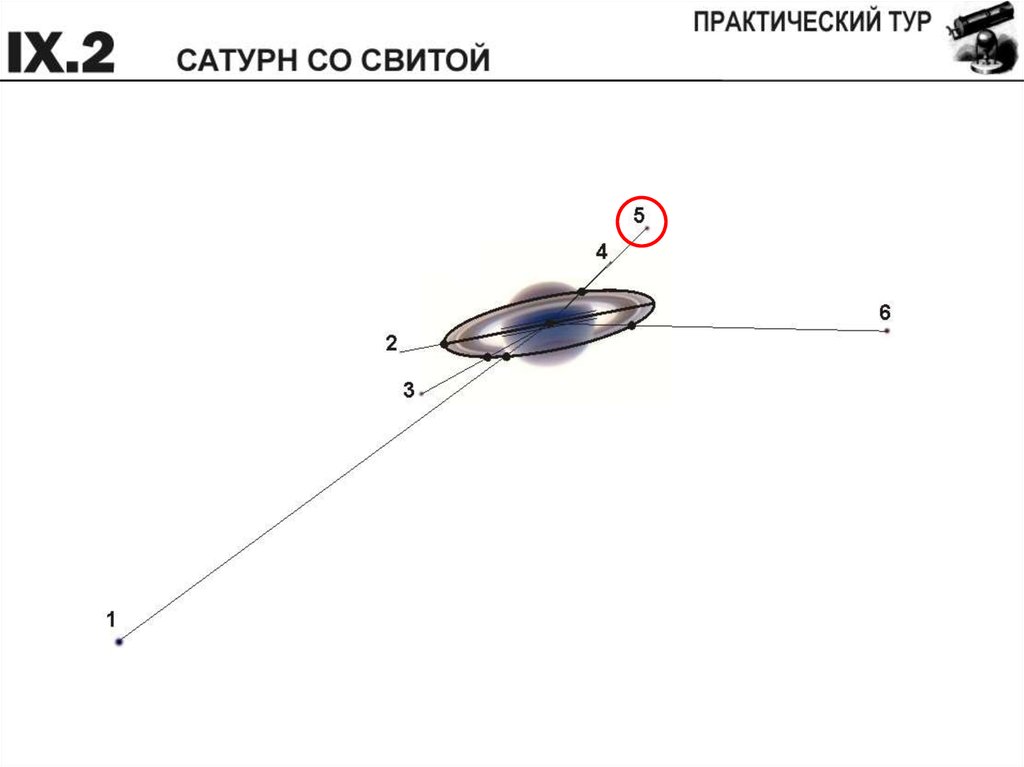
идентифицируйте спутники на фотографии. Укажите, какой из всех
изображенных спутников в момент съемки находился ближе всех к
Земле. Считайте, что все кольца и все спутники находятся в одной
плоскости, орбиты спутников круговые. Данные о наиболее
крупных спутниках Сатурна приведены в таблице.
8.
Кольцо и спутники – в одной плоскости!9.
10.
11.
Система оценивания:Построение метода вычисления расстояний
8
(плоскость рисунка или яркость)
(2)
Отождествление спутников
Определение ближайшего спутника
12 (6x2)
4
ИТОГО
24
12.
Астрономы из команды ASAS-SN, патрулирующие небо в поискахсверхновых звезд, обнаружили на снимке 5 июля 2016 года объект,
которого не было на снимке от 26 июня 2016 года. В первом
сообщении было объявлено, что найдена новая сверхновая в
далекой галактике NGC 4725, но позже оказалось, что
обнаруженный объект – это карликовая планета Макемаке. По
предоставленной фотографии определите, за сколько дней до
обнаружения Макемаке появилась в кадре? Считать, что во время
наблюдений Макемаке была в противостоянии с Солнцем на
расстоянии 51 а.е. от Земли.
13.
Орбитальная скоростьМакемаке: v < v0/7.
Угловая скорость
в противостоянии:
w = v0/L = 0.02 в день.
T = 4 дня.
4.5’
14.
Система оценивания:Определение угловой скорости
12
(Учет орбитального движения Макемаке)
(=)
Размер поля зрения кадра
Определение времени
6
6
ИТОГО
24
Гелиоцентрическая угл.скорость
Движение по диагонали
10
18
15.
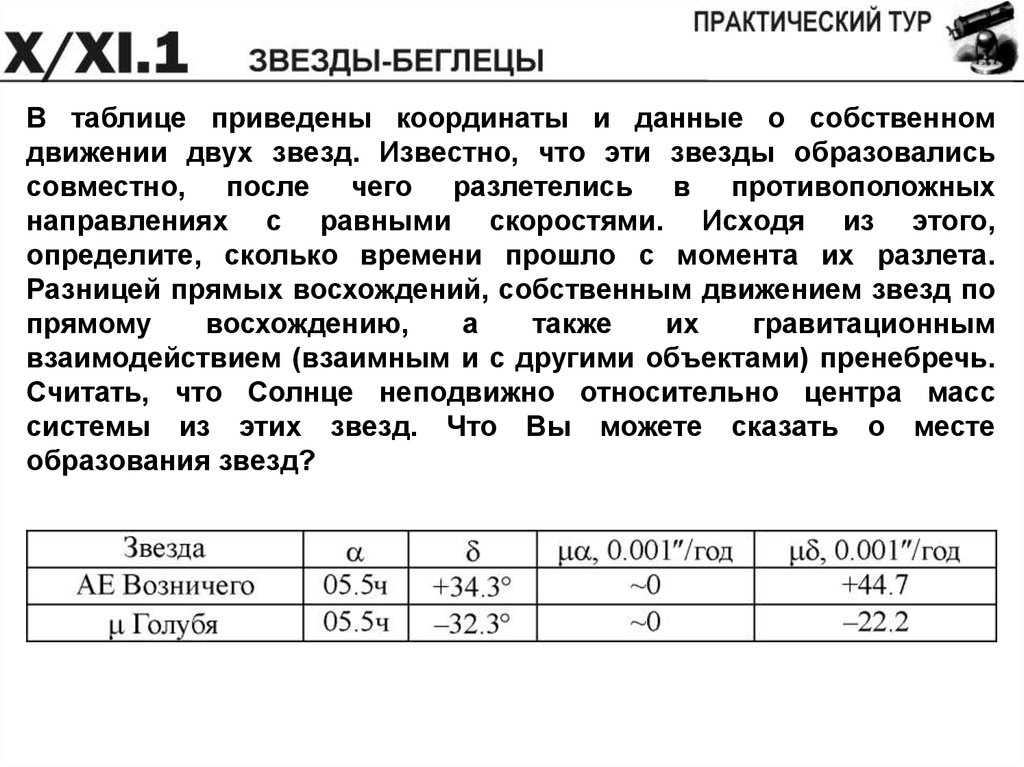
В таблице приведены координаты и данные о собственномдвижении двух звезд. Известно, что эти звезды образовались
совместно, после чего разлетелись в противоположных
направлениях с равными скоростями. Исходя из этого,
определите, сколько времени прошло с момента их разлета.
Разницей прямых восхождений, собственным движением звезд по
прямому
восхождению,
а
также
их
гравитационным
взаимодействием (взаимным и с другими объектами) пренебречь.
Считать, что Солнце неподвижно относительно центра масс
системы из этих звезд. Что Вы можете сказать о месте
образования звезд?
16.
AE Aur??
m Col
17.
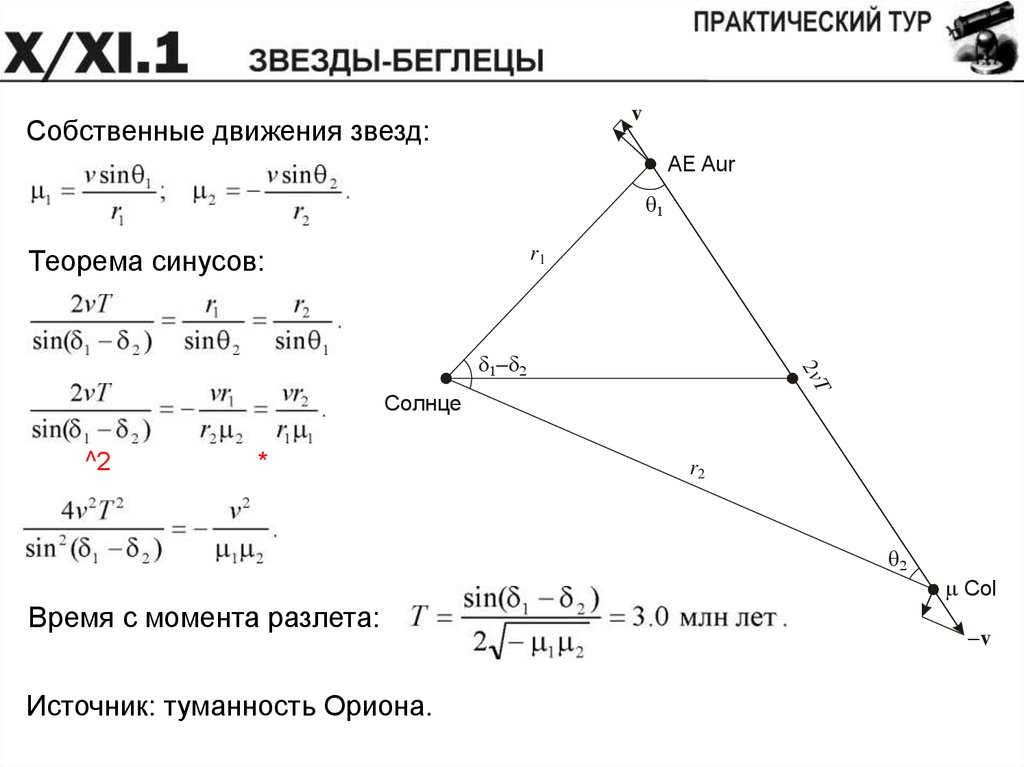
vСобственные движения звезд:
AE Aur
r1
Теорема синусов:
2vT
Солнце
^2
*
r2
m Col
Время с момента разлета:
Источник: туманность Ориона.
v
18.
Система оценивания:Правильная геометрическая картина
12
(Постоянное собственное движение)
(0)
Вычисление времени
Определение места происхождения
8
4
ИТОГО
24
Указание правильной картины,
но вычисление из m=const, 1-2 этапы
≤12
19.
Перед Вами фотография, сделанная с борта АМС "Кассини". Наней видны три спутника Сатурна – Титан, Мимас и Рея. Оцените по
фотографии длительность сумерек (в земных часах) на экваторе
Титана.
20.
Эффект 1: увеличение фазыd
Рея:
x
Рея
l0
Титан:
D
A
Титан
L0
L1
21.
Солн
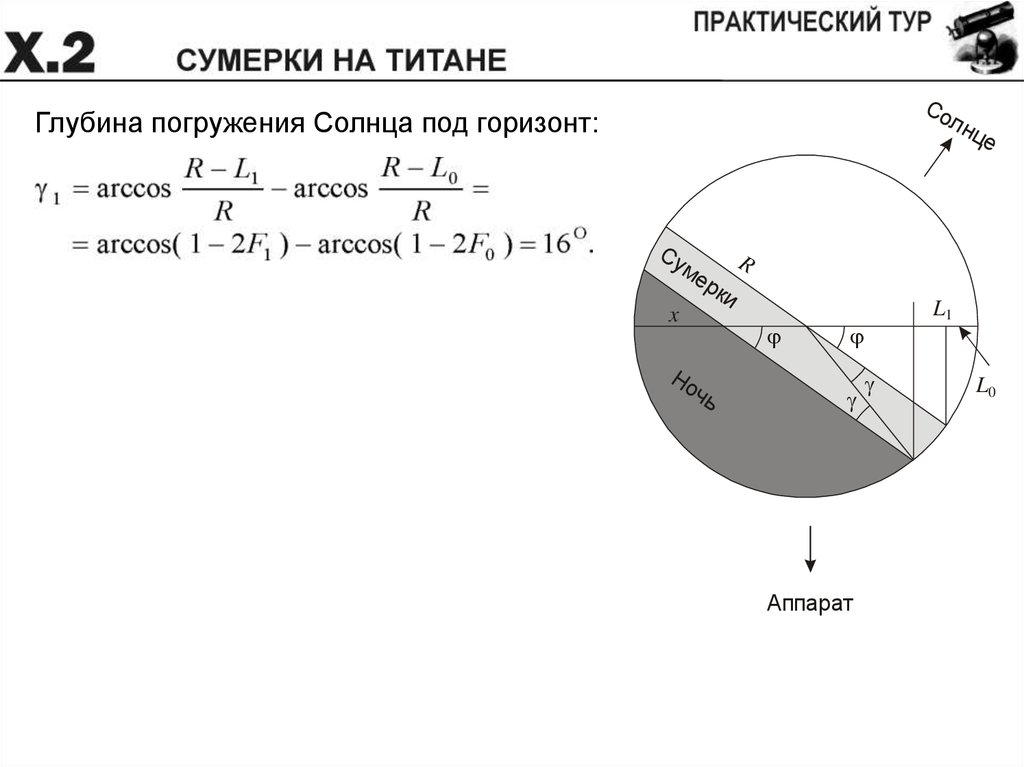
Глубина погружения Солнца под горизонт:
Су
ме
р
x
Но
чь
це
R
ки
L1
Аппарат
L0
22.
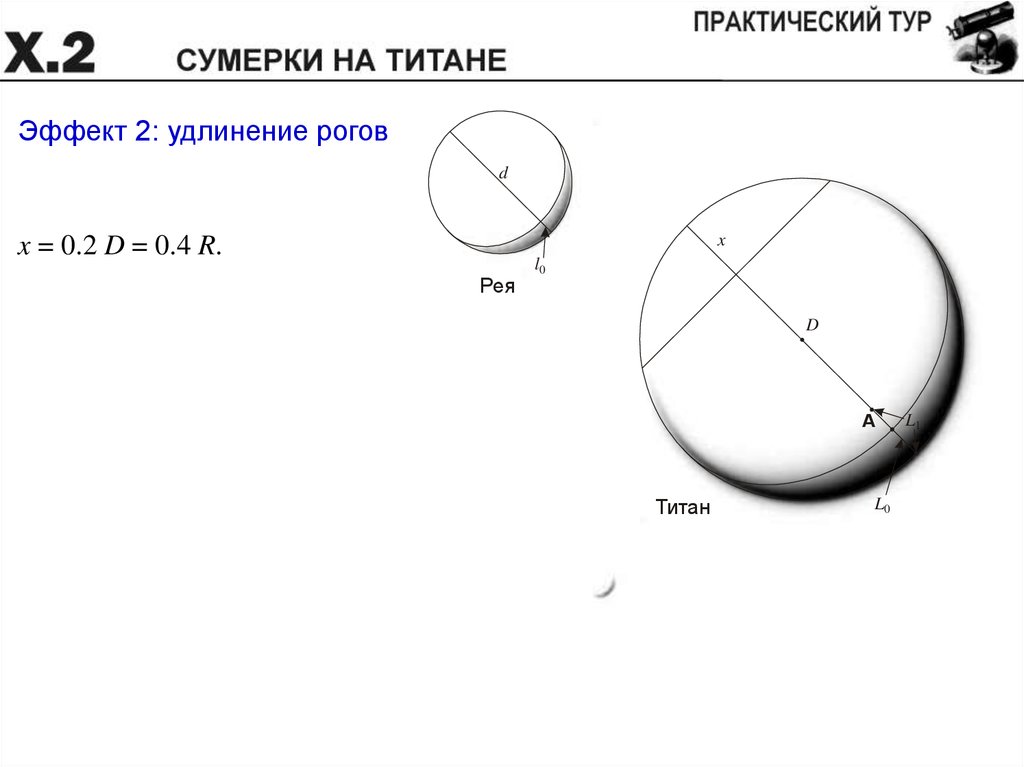
Эффект 2: удлинение роговd
x
x = 0.2 D = 0.4 R.
Рея
l0
D
A
Титан
L0
L1
23.
Солн
Глубина погружения Солнца под горизонт:
Су
ме
р
x
= 18 , T = 16 дней
Но
чь
R
ки
L1
Равноденствие:
Солнцестояние: *1/cos(27 ) → 21.5 час.
це
Аппарат
L0
24.
Система оценивания:Указание Титана
Угол погружения Солнца
4
12
(Описание – 6, вычисления – 6)
Осевой и орбитальный период равны
Длительность сумерек: равноденствие
Длительность сумерек: солнцестояние
2
4
2
ИТОГО
24
25.
Перед Вами карта видимости покрытия звезды TYC 2428-01094-1(видимая величина 11.5m) астероидом Каллиопа 24 марта 2017 года
с 16ч57м до 17ч08м по Всемирному времени, видимого на
территории России (моменты времени в минутах указаны на
карте). Земля изображена, как она наблюдается со стороны
астероида. Дневная часть поверхности Земли заштрихована
сплошными линиями, сумеречная – пунктирными линиями.
Координаты звезды: a=6ч17.6м, =+34 39 . Астероид принадлежит
главному поясу. Считая его орбиту круговой, определите
расстояние от Земли до астероида в момент покрытия.
26.
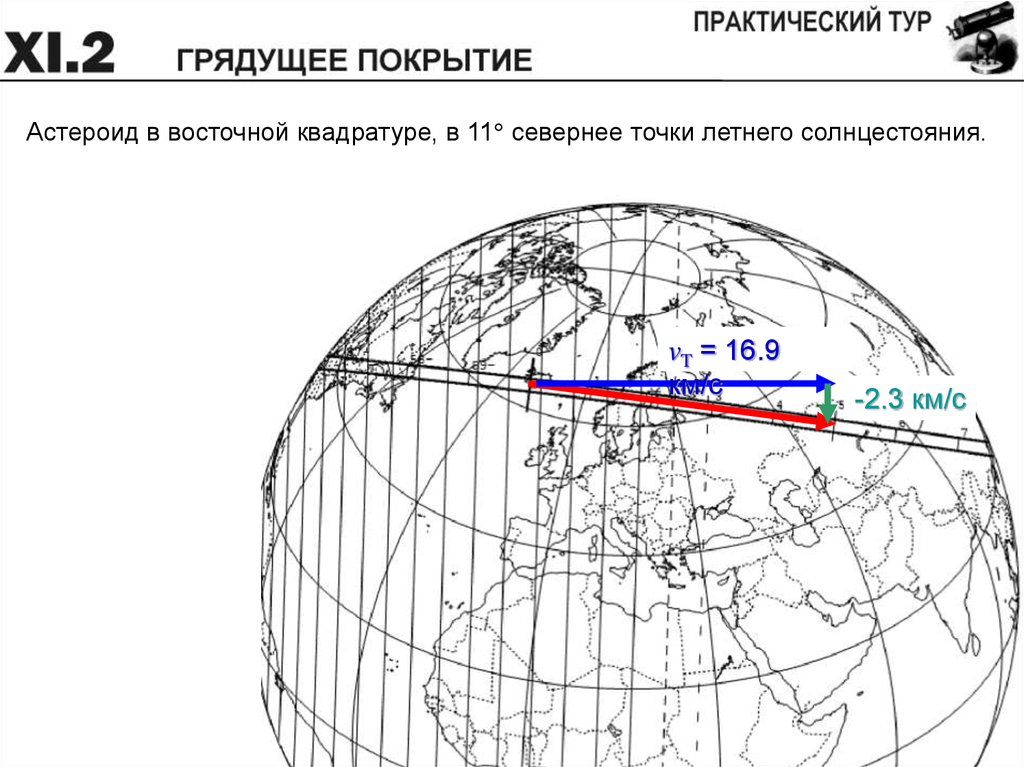
Астероид в восточной квадратуре, в 11 севернее точки летнего солнцестояния.vT = 16.9
км/c
-2.3 км/с
27.
vVvR
vT
Астероид
ка
и
т
п
Экли
Эк
ва
то
р
Звезда
Солнце
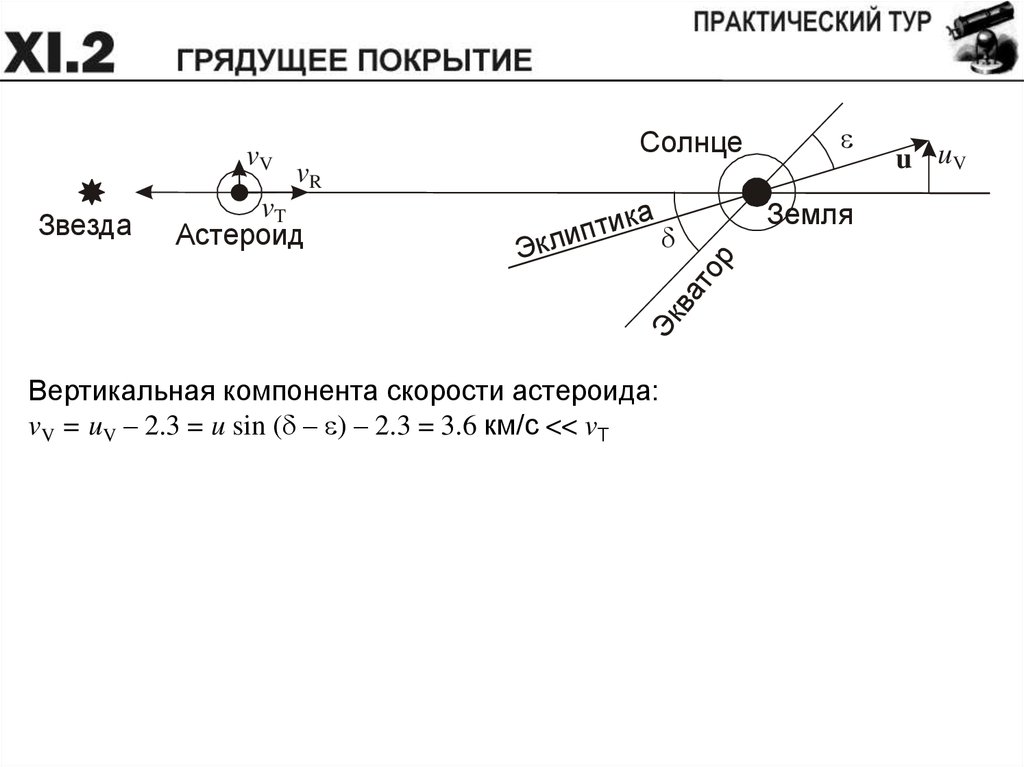
Вертикальная компонента скорости астероида:
vV = uV – 2.3 = u sin ( – ) – 2.3 = 3.6 км/c << vT
Земля
u uV
28.
СолнцеКруговые орбиты:
L
Астероид
vT
x3 – x + C = 0.
x<1: x0 = C = 0.32,
Расстояние до астероида:
Реально: 2.54 а.е.
vR a
l
D
Земля
v
x = 0.37.
29.
Система оценивания:Астероид в квадратуре
4
(либо нахождение углового расстояния от Солнца)
Геоцентрическая скорость астероида
6
(только горизонтальная)
(4)
Гелиоцентрическая скорость (выражение)
Вычисление расстояния до астероида
6
8
ИТОГО
24
v = vT, a = 0
14
30.
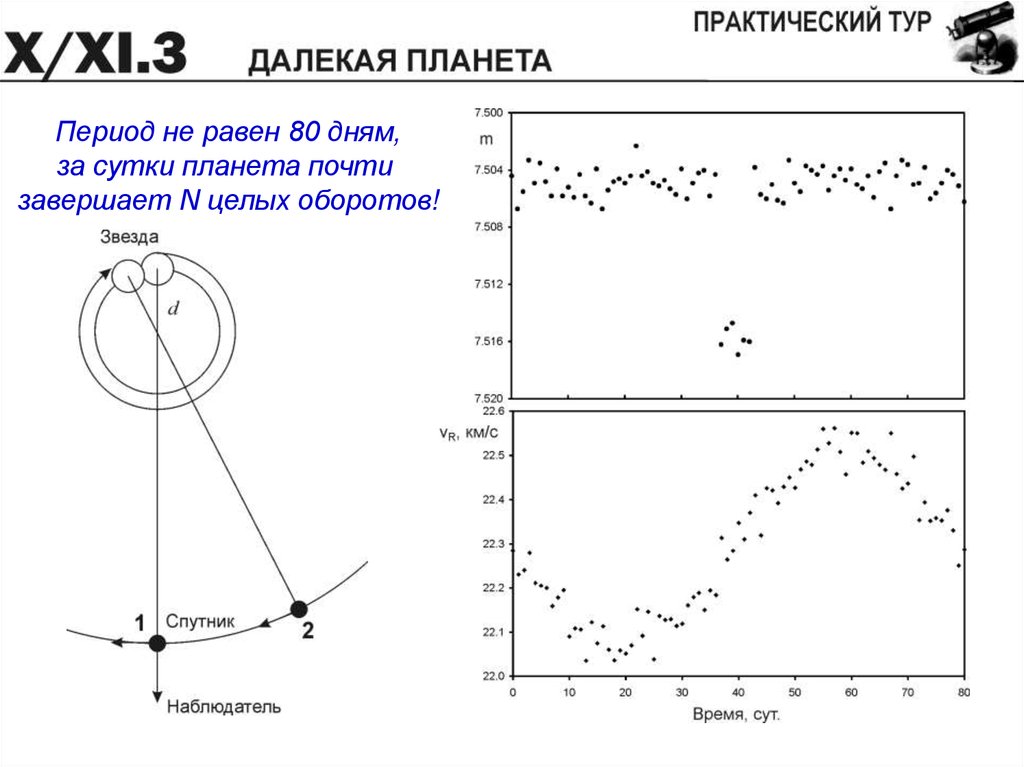
Около звезды с массой, равной массе Солнца, был обнаружентемный спутник. В некоторой обсерватории с интервалом ровно в
1 сутки производились одновременные измерения видимой
звездной величины и гелиоцентрической лучевой скорости
звезды, результаты представлены на графиках. Определите
радиус звезды, массу и радиус спутника. Считать, что
наблюдатель располагается в плоскости круговых орбит системы,
а оба тела имеют сферическую форму. Других массивных тел в
этой системе нет. Эффект потемнения звезды к краю не учитывать.
Что из себя представляет эта звезда и чему равно расстояние до
нее?
31.
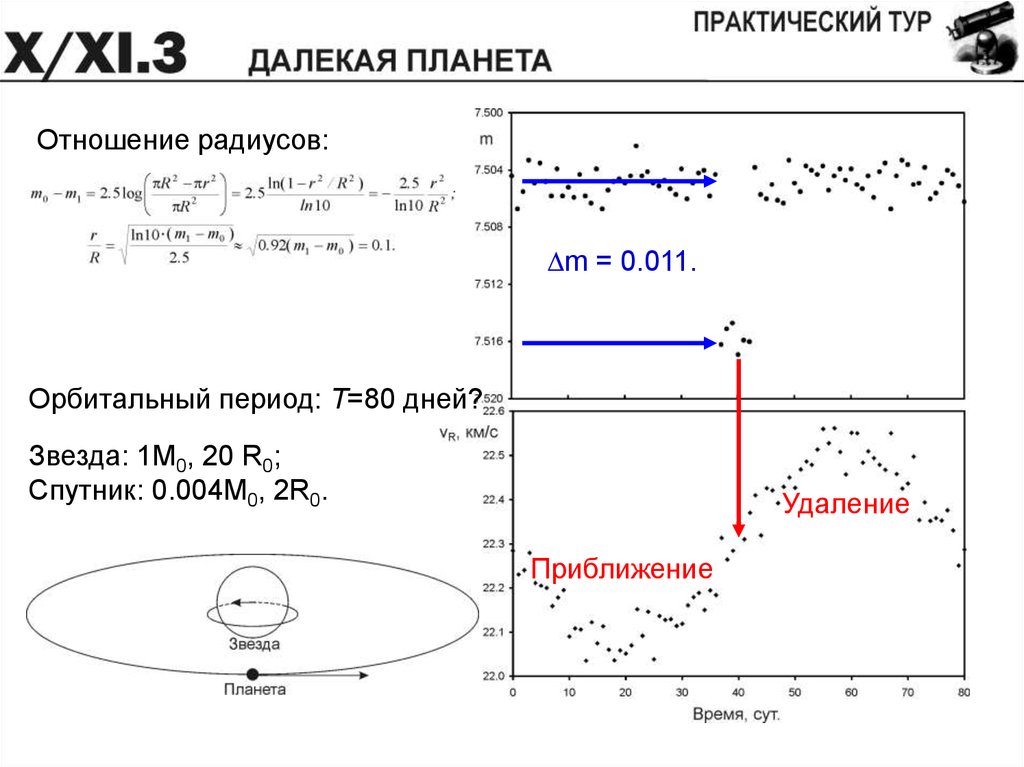
Отношение радиусов:Dm = 0.011.
Орбитальный период: T=80 дней?
Звезда: 1M0, 20 R0;
Спутник: 0.004M0, 2R0.
Удаление
Приближение
32.
Период не равен 80 дням,за сутки планета почти
завершает N целых оборотов!
33.
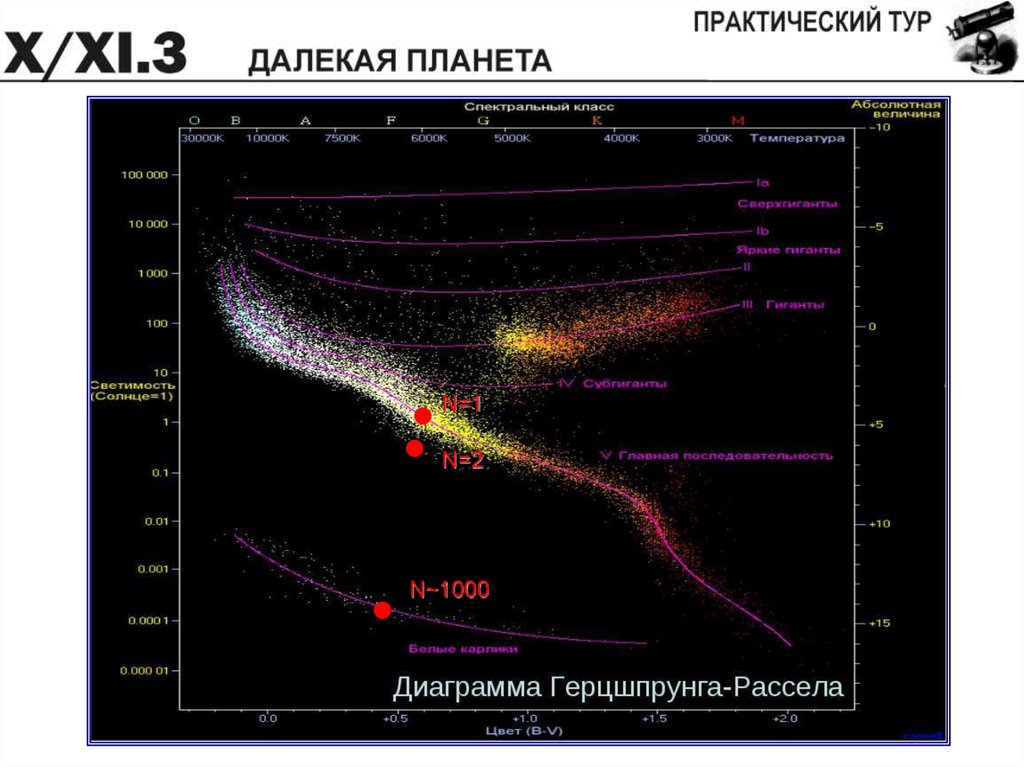
Орбитальный период:Радиус орбиты спутника: a = (T, годы)2/3 = 3 млн км / N2/3.
Затмение: 6/80 от орбитального периода. Радиус звезды:
34.
N=1N=2
N~1000
35.
Орбитальная скорость звезды: v ~ 0.2 км/сРадиус орбиты звезды:
Отношение масс:
N~1000: Спутник с радиусом 600 км и массой 0.1 массы Юпитера!
N=1: Спутник совпадает с Юпитером по массе и радиусу,
звезда аналогична Солнцу.
Видимая звездная величина +7.5: расстояние – 35 пк.
36.
Система оценивания:Возможные значения орбитального периода
8
(T = 80 сут)
(T = 1 сут, N=1)
(0)
(6)
Соотношение радиусов
Выражение для радиуса звезды
2
Выражение для массы планеты
Анализ возможных чисел N
Тип звезды (Солнце, только при правильных выводах)
Расстояние до системы (только при правильных выводах)
2
ИТОГО
24
Т=80 сут (только этапы 2-4)
Т=1 сут (N=1 без обоснования)
8
18
4
4
2
2






















 Астрономия
Астрономия








