Похожие презентации:
Неопределенный интеграл
1.
§30. Неопределенныйинтеграл
п.1. Первообразная.
Функция
называется первообразной
для функции
на интервале
, если
x (a; b)
F '(x) f (x)
Пример. (?)' 2 x
x ; x 1; x 2
2
f ( x) 2 x F (x) x C
2
2
2
2.
Теорема 1. Если функция F ( x ) являетсяпервообразной для функции f ( x )
на интервале ( a ; b ), то множество
всех первообразных задается
формулой
F (x) C ,
C ― произвольная постоянная
3.
Доказательство.( F ( x ) C )' F ' ( x ) ( C )' f ( x )
F ( x ) C ― первообразная для f ( x )
( x ) ― первообразная для f ( x )
(x) F (x)
( ( x ) F ( x ))' ' ( x ) F ' ( x ) f ( x ) f ( x ) 0
(x) F (x) C
4.
Неопределенным интеграломот функции f ( x ) называется множество всех
первообразных этой функции.
f ( x ) dx F ( x ) C
Всякая непрерывная функция на
интервале ( a ; b ) имеет на этом интервале
первообразную, а значит и неопределенный
интеграл.
5.
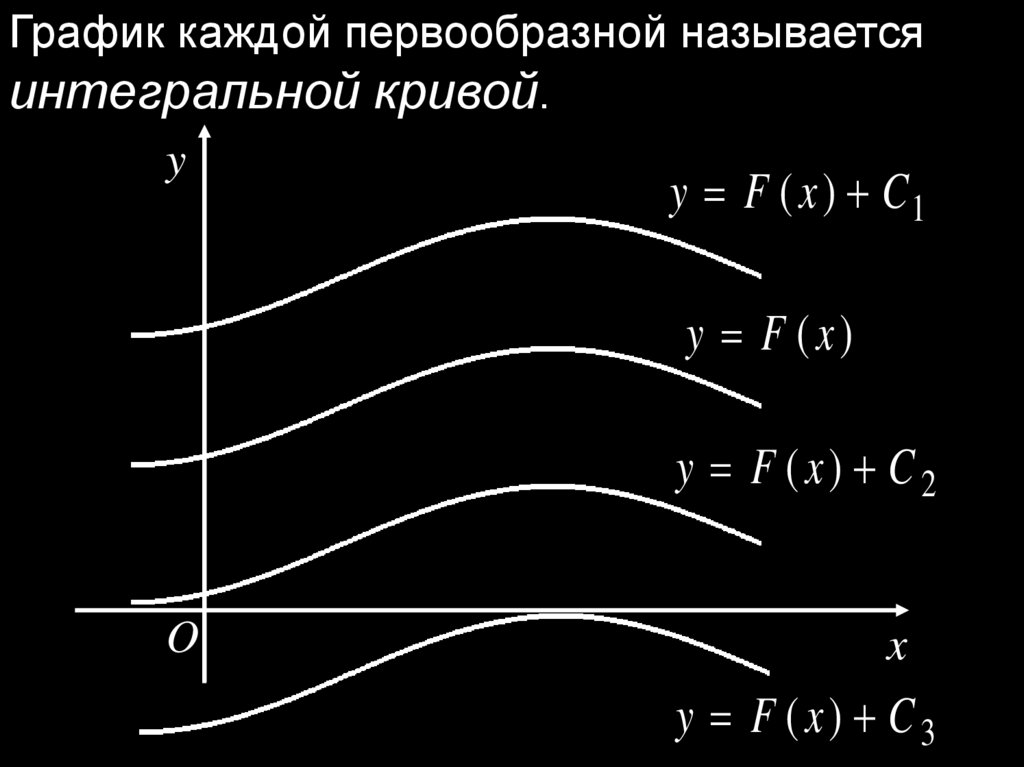
График каждой первообразной называетсяинтегральной кривой.
y
y F ( x ) C1
y F (x)
y F (x) C 2
O
x
y F (x) C3
6.
п.2. Свойства неопределенногоинтеграла.
1. Производная от неопределенного интеграла
равна подынтегральной функции.
f ( x ) dx f ( x )
'
Доказательство.
f ( x ) dx F ( x ) C F ' ( x ) (C )' f ( x )
'
'
7.
2. Дифференциал от неопределенногоинтеграла равен подынтегральному
выражению.
d f ( x ) dx f ( x ) dx
Доказательство.
d f ( x ) dx d F ( x ) C dF ( x ) d ( C )
F '( x)dx f ( x)dx
§9 п.2
8.
3. Неопределенный интеграл отдифференциала некоторой функции равен
сумме этой функции и произвольной
константы.
dF
(
x
)
F
(
x
)
C
Доказательство.
dF ( x ) F ' ( x ) dx f ( x ) dx F ( x ) C
9.
4. Постоянный множитель можно выносить зазнак интеграла.
5. Неопределенный интеграл от суммы
конечного числа функций равен сумме
интегралов от слагаемых функций.
( af ( x ) bg ( x )) dx a f ( x ) dx b g ( x ) dx ,
a,b R
Пример.
(
3
x
7
e
4
)
dx
3
x
dx
7
e
dx
4
dx
2
x
2
x
x 7e 4 x C
3
x
10.
п.3. Таблица интегралов.a 1
x
sin x dx cos x C
a
1
x
dx
C
,
a 1
dx
cos
x
dx
sin
x
C
ln
|
x
|
C
x
x
a
dx
a
0
,
x
tg
x
C
a
dx
C
,
2
a
1
ln a
cos x
dx
x
x
sin 2 x ctg x C
e dx e C
a
11.
dx1
x
a 2 x 2 a arctg a C , a 0
dx
x
a 2 x 2 arcsin a C , a 0
1
x a
ln
C
,
a
0
x 2 a 2 2a x a
dx
dx
x 2 a 2 ln x x a C , a 0
2
2
12.
п.4. Простейшие методыинтегрирования.
I. Метод интегрирования подстановкой
(замена переменной).
x 2 t
( x 2)' dx dt
100
100
100
(t 2)t dt
x( x 2) dx dx dt
x t 2
Пример.
102
101
102
101
t
t
(
x
2
)
(
x
2
)
101
100
t 101
dt 2 t 100
dt
2
C
2
C
102
101
102
101
13.
Теорема 2. (О замене переменной внеопределенном интеграле)
Пусть
функция x (t ) определена и
дифференцируема на промежутке T и X ―
множество ее значений,
функция y f ( x ) определена на множестве X
и имеет на этом множестве первообразную.
Тогда
f
(
x
)
dx
x ( t )
f ( ( t )) ' ( t ) dt .
14.
Доказательство.F ( x ) ― первообразная для f ( x )
f ( x ) dx x ( t ) F ( x ) C x ( t ) F ( (t )) C
F ( ( t )) F ' ( x ) ' ( t ) f ( x ) ' ( t )
'
Теорема 4 §8
F ( ( t )) ― первообразная для f ( x ) ' ( t )
f ( ( t )) ' ( t ) dt F ( ( t )) C
15.
II. Метод интегрирования по частям.Теорема 3.
Пусть
функции u u ( x ) и v v ( x ) дифференцируемы
на промежутке X,
существует
.
v
(
x
)
u
'
(
x
)
dx
Тогда
существует u ( x ) v ' ( x ) dx
и справедлива формула
dv v ' dx
udv uv v du. du u ' dx
16.
Доказательство.( u v )' u ' v u v ' u v ' ( u v )' u ' v
(uv )' имеет первообразную uv
u' v
имеет первообразную
u
'
v
dx
uv ' имеет первообразную uv 'dx
uv
uv'
'
dx
(
uv
)'
(
u
'
v
)
dx
(
uv
)'
dx
(
u
'
v
)
dx
uv u ' vdx
dv v ' dx
du u ' dx
udv uv v du
17.
Пример.u ln x
u ln x
udv lnxdx
x
dv xdx
2
2
dv xdx
x
x 1
1
dx
x dx du (ln x )' dx 1 dx ln x
x ln xdx
2
2 x
du (ln x )' dx x dx
2 x
udv v xdx x
uv v du
2
2
2
2
x
x
x
ln x xdx ln x
C
2
2
4















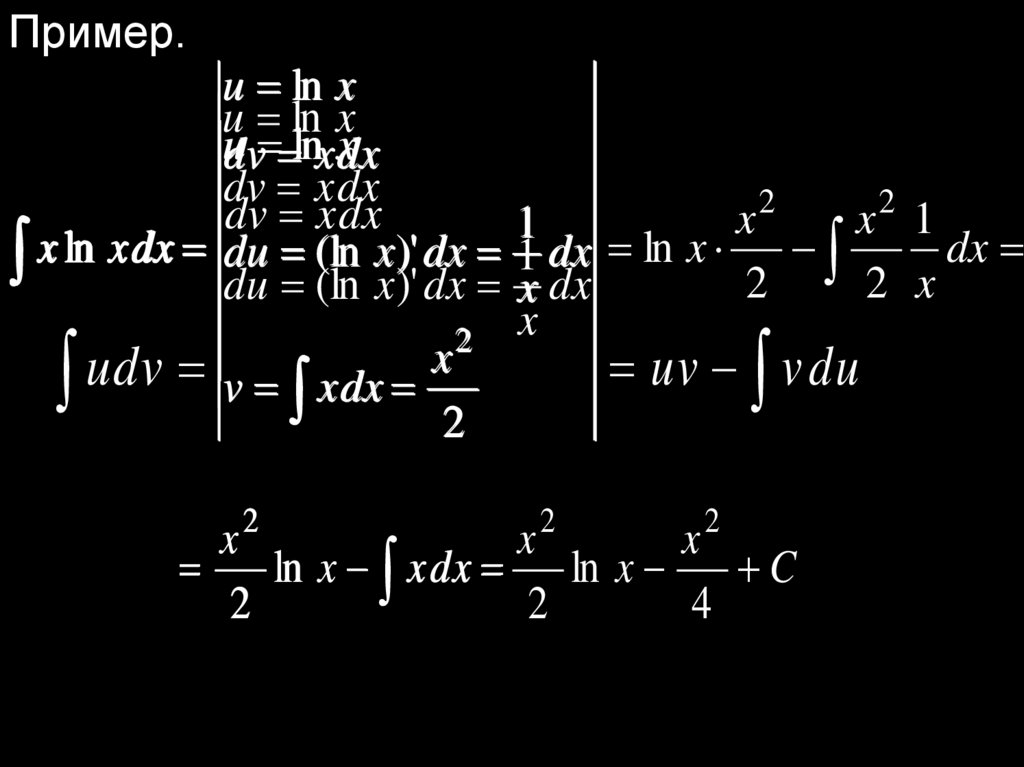
 Математика
Математика








