Эйлеров граф

1.

Эйлеров граф
Выполнил студент 4 курса
Пронин Кирилл Дмитриевич

2.

На вебинаре мы с вами рассмотрим:
1. Что такое граф
2. Применения теории графов
3. Графы, которые можно нарисовать одним росчерком
– не отрывая карандаша от бумаги.
4. Некоторые задачи по теме

3.

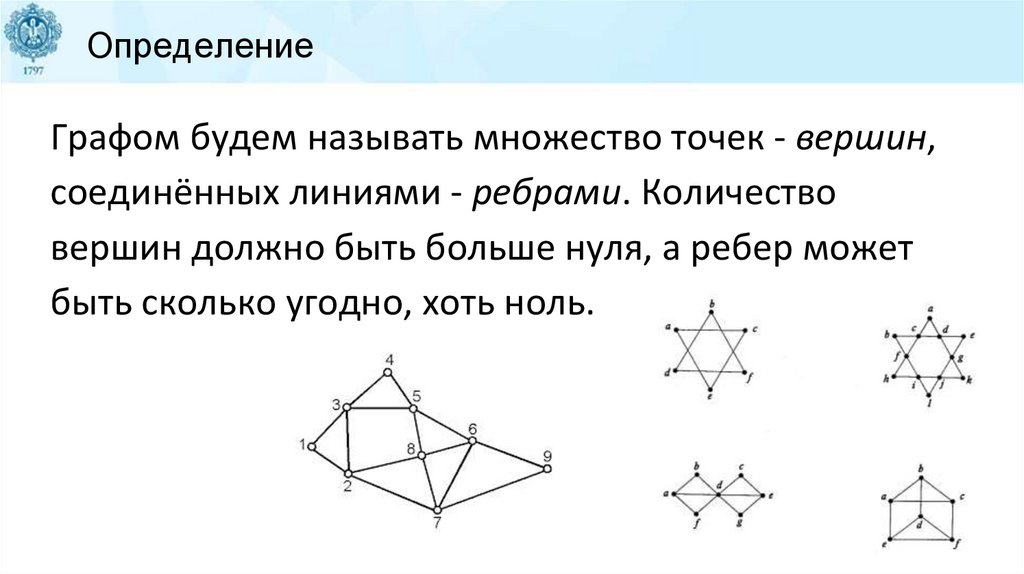
Определение
Графом будем называть множество точек - вершин,
соединённых линиями - ребрами. Количество
вершин должно быть больше нуля, а ребер может
быть сколько угодно, хоть ноль.

4.

Историческая справка
Швейцарский, прусский и российский математик Леонард Эйлер в статье о
решении знаменитой задачи о кёнигсбергских мостах, датированной 1736
годом, первым применил идеи теории графов при доказательстве
некоторых утверждений. Именно он считается отцом теории графов,
открывшим понятие графа, а 1736 - год рождения теории графов.

5.

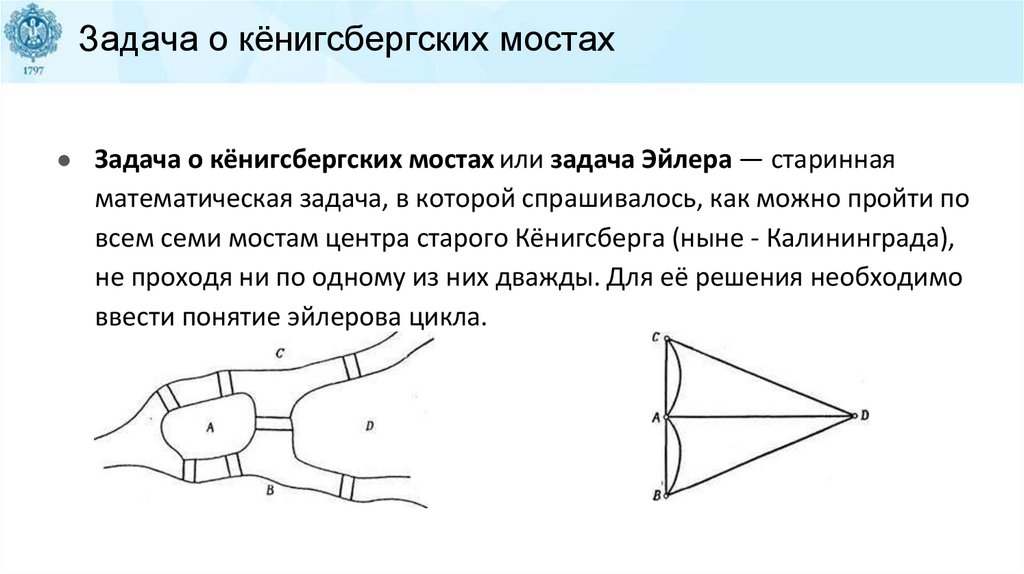
Задача о кёнигсбергских мостах
● Задача о кёнигсбергских мостах или задача Эйлера — старинная
математическая задача, в которой спрашивалось, как можно пройти по
всем семи мостам центра старого Кёнигсберга (ныне - Калининграда),
не проходя ни по одному из них дважды. Для её решения необходимо
ввести понятие эйлерова цикла.

6.

Эйлеров цикл
Эйлеров цикл — это маршрут по вершинам и рёбрам графа, который
проходит по каждому ребру ровно один раз и возвращается в исходную
вершину.
Граф, содержащий Эйлеров цикл называется “эйлеровым графом”.

7.

Теорема
Необходимое условие: В Эйлеровом графе каждая вершина является
концом чётного числа рёбер.
Доказательство: Если граф Эйлеров, то начав в любой его вершине, мы
сможем обойти все рёбра. Посетив очередную вершину маршрута, мы
должны будем покинуть её, пока не вернёмся в исходную вершину. Таким
образом, каждая вершина будет посещена чётное количество раз на
пути. Исходная же вершина помимо этого будет являться концом ребра
из которого мы начинали маршрут и концом ребра, на котором мы его
закончили, а значит тоже будет концом чётного числа рёбер.

8.

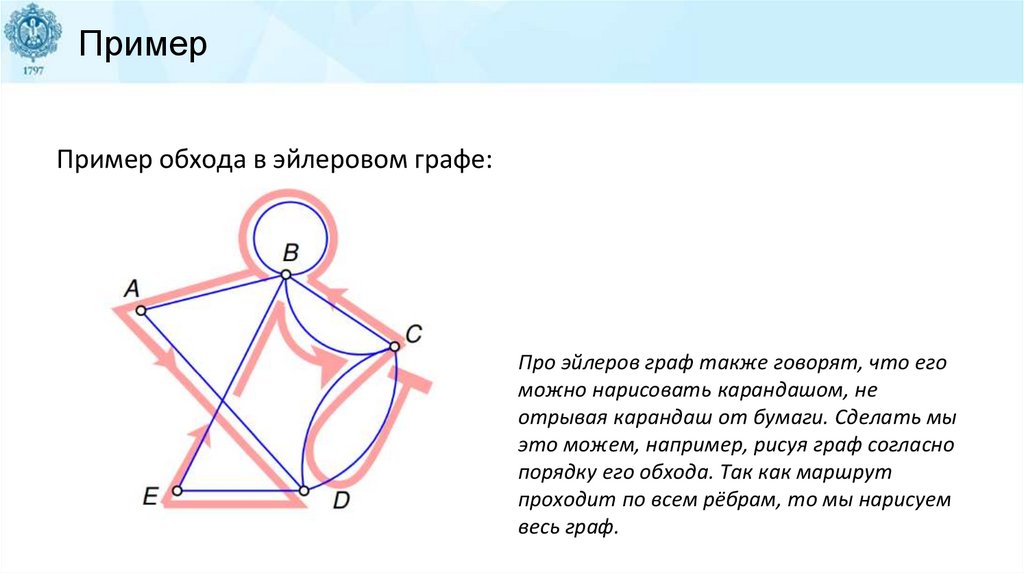
Пример
Пример обхода в эйлеровом графе:
Про эйлеров граф также говорят, что его
можно нарисовать карандашом, не
отрывая карандаш от бумаги. Сделать мы
это можем, например, рисуя граф согласно
порядку его обхода. Так как маршрут
проходит по всем рёбрам, то мы нарисуем
весь граф.

9.

Задачи
Дана проволока длиной 12 см. Можно ли сложить из нее каркас куба с ребром в 1 см?
Проволоку нельзя резать.
Решение: У куба 12 рёбер по 1 см, а у нас есть ровно 12 см проволоки. Значит, делать
двойные рёбра нельзя, иначе нам не хватит проволоки. Каркас куба можно изобразить в виде
графа (см. рис.) Если бы каркас можно было сложить из проволоки, не разрезая её, то и граф
можно было бы нарисовать, не отрывая карандаша от бумаги (рисуя рёбра в том порядке, в
котором мы делаем их из проволоки). А это невозможно в силу предыдущей задачи: ведь у
этого графа целых восемь вершин степени 3.

10.

Задачи
Дан план квартиры: комнаты и двери. Можно ли обойти квартиру так, чтобы через каждую дверь
пройти ровно по одному разу?
Решение: Комната — вершина, двери — ребра. Тогда степени вершин: 5, 5, 5, 4, 4. Есть
еще одна вершина - наружное пространство. Туда выходит 9 дверей - 9 ребер. Это еще
одна вершина, со степенью 9. Больше двух вершин не чётные, значит нельзя.

11.

Итоги нашего вебинара
1. Мы познакомились с понятием графа и эйлерова графа.
2. Разобрали теорему Эйлера и задачу о Кёнигсбергских мостах.
3. Решили несколько задач с применением теории графов.

12.

Спасибо за внимание!!!