Похожие презентации:
Методы компиляции. Лекция 2
1.
ТОМСКИЙ ГОСУДАРСТВЕННЫЙ УНИВЕРСИТЕТКостюк Ю. Л.
МЕТОДЫ КОМПИЛЯЦИИ
Лекция 2
1
2.
АВТОМАТНЫЕ ГРАММАТИКИ И ЯЗЫКИКласс 3: автоматные грамматики (А-грамматики).
Вид порождающих правил:
A → aB или A → a
где A, В – нетерминалы, a – терминал.
Пример автоматной грамматики
Грамматика: G2(L) = {∑, N, S, P}
∑ = {a, b}, N = {S, T}, S = {S},
P = {S → aS, S → bT, T → bT, T → a}.
Процесс порождения:
S => aS => abT => aba,
S => bT => bbT => bbbT => bbba , . . .
Со второго шага порождения цепочка имеет вид:
γA,
где γ – терминальная цепочка, A – нетерминал, на последнем
шаге нетерминал А заменяется на терминал.
2
3.
РАСПОЗНАВАТЕЛЬ АВТОМАТНОЙГРАММАТИКИ – КОНЕЧНЫЙ АВТОМАТ
Конечный автомат – это частный вид машины Тьюринга, в
которой:
1) лента является входной, на каждом шаге работы
автомата с неё считывается очередной символ;
2) на каждом шаге работы автомата устройство
управления делает переход в новое состояние в
соответствии с правилами перехода.
Устройство
управления
3
4.
Конечный автомат задается пятеркой множеств:{Σ, Q, q0, F, δ},
где Σ – множество (алфавит) входных символов;
Q – множество состояний автомата;
q0 – начальное состояние q0 Q ;
F – множество заключительных состояний F Q ;
δ – множество правил перехода, имеющих вид:
(a, qi) → qj,
Правило перехода задаёт переход из состояния qi,
когда на входе читается символ a, в состояние qj.
5.
РАСПОЗНАВАТЕЛЬ АВТОМАТНОЙГРАММАТИКИ – КОНЕЧНЫЙ АВТОМАТ
Начало работы: считывающая головка автомата
обозревает самый левый символ на ленте;
автомат находится в начальном состоянии q0.
На очередном шаге – переход в новое состояние в
соответствии с правилом перехода:
(a, qi) → qj,
лента продвигается влево на один символ.
Если прочитаны все символы на ленте и автомат
находится в заключительном состоянии, то говорят,
что входная цепочка успешно распознана (допущена)
автоматом.
В противном случае - цепочка не допущена.
5
6.
КОНЕЧНЫЙ АВТОМАТ: РЕАЛИЗАЦИЯ1. Справа после входных символов на ленте автомата –
«пустая» клетка (символ «┴»), не принадлежащий
алфавиту ∑.
2. Каждому нетерминалу грамматики соответствует
одно состояние конечного автомата.
3. В грамматику добавляется еще один нетерминал Z,
ему соответствует заключительное состояние.
Правила вида: A → a заменяются на: A → aZ,
кроме того, добавляется правило: Z → ┴.
4. Успешному распознаванию в работе конечного
автомата соответствует следующая ситуация:
• головка автомата обозревает символ «┴»;
• автомат находится в заключительном
состоянии.
Тогда входная цепочка допущена автоматом. 6
7.
ПРИМЕР КОНЕЧНОГО АВТОМАТАГрамматика: G2(L) = {∑, N, S, P}
∑ = {a, b}, N = {S, T },
S = {S},
P = {S → aS, S → bT, T → bT, T → a}. Замена T → a на T → aZ .
Добавление: Z → ┴. Автомат в виде таблицы:
Входной символ_
Состояние
a
b
S
T
Z
S
Z
T
T
┴
допуск
Примеры: a a a b b a ┴
a b ┴
↑ ↑ ↑
↑ ↑
SSSSTT Z
S ST
S S T Z
↑ ↑ ↑ ↑ ↑ ↑
↑
a b a a ┴
↑
↑
7
8.
РЕАЛИЗАЦИЯ ДЕТЕРМИНИРОВАННОГОКОНЕЧНОГО АВТОМАТА
Входная цепочка: массив C,
Номер текущего символа: i,
Состояние s: 1, 2, . . . , k, k+1.
Начальное: 1, заключительное: k, ошибочное: k+1.
Матрица переходов: массив M.
Таблица перекодировки (символ -> номер столбца): T.
i:=1; s:=1;
while s<k do begin
{i <= длины строки С}
j:=T[ord(C[i])];
s:=M[s,j];
i:=i+1
end;
if (s=k)and(C[i]=’┴’) then «допуск» else «нет»
Трудоемкость: O(n)
8
9.
НЕДЕТЕРМИНИРОВАННЫЙ КОНЕЧНЫЙАВТОМАТ
Грамматика: G3(L) = {∑, N, S, P}
∑ = {a, b}, N = {S, T, C},
S = {S},
P = {S → aT, S → aC, T → aT, T → aC, T → bC, C → bC, C → b}.
Замена: C → b на C → bZ.
Входной символ_
Добавление: C → ┴
┴
a
b
Состояние
Недетерминированности:
S
T/C
{S → aT, S → aC},
T
T/C C
{T → aT, T → aC},
{C → bC, C → bZ}
C
C/Z
Z
Примеры: a
a
b
b
↑
↑
↑
↑
S
T/C T/C C/Z C/Z
допуск
┴
↑
9
10.
РЕАЛИЗАЦИЯ НЕДЕТЕРМИНИРОВАННОГОКОНЕЧНОГО АВТОМАТА
Входная цепочка: массив C, Номер текущего символа: i,
Состояние s: битовый вектор длиной k бит.
Начальное: (1,0,0, . . . 0) заключительное: (?, ?, ?, . . . , ?, 1)
ошибочное: (0,0,0, . . . 0)
Матрица переходов: массив M из битовых векторов длиной k.
Таблица перекодировки (символ -> номер столбца): T.
i:=1; s:=(1,0,0, . . . 0);
while (s<>(0,0,0, . . . 0))and(C[i]<>’┴’) do {i<=длины строки С}
begin
j:=T[ord(C[i])];
s1:=(0,0,0, . . . 0);
for p:=1 to k do
if s[p]=1 then s1:=s1 or M[p,j];
s:=s1;
i:=i+1
end;
if (s[k]=1)and(C[i]=’┴’) then «допуск» else «нет»
Трудоемкость: O(k2 n) или O(k n)
10
(при использовании битово-векторных операций)
11.
ПРЕОБРАЗОВАНИЕ НЕДЕТЕРМИНИРОВАННОЙАВТОМАТНОЙ ГРАММАТИКИ К ДЕТЕРМИНИРОВАННОЙ
Пусть в грамматике (с добавленным нетерминалом Z) есть
недетерминированность:
{A → bB1, A → bB2, . . . , A → bBn}.
(*)
Обозначим: B*={B1, B2, . . . , Bn}.
Вместо порождающих правил (*) добавим правило:
A → bB*
В дополнение к правилам {B1→β1, B2→β2, . . . , Bn→βn} добавим правила:
{B*→β1, B*→β2, . . . , B*→βn}.
Преобразованная грамматика будет порождать в точности то же самое
множество цепочек, что и исходная грамматика, т.е. язык не изменится.
Применим такое же преобразование ко всем другим недетерминированностям, в результате грамматика станет детерминированной. Общее количество имевшихся в исходной грамматике нетерминалов и вновь добавленных не более чем 2k, где k – количество имевшихся в исходной грамматике нетерминалов.
____________________________________________________________________________________________________________________________________
Теорема: любую недетерминированную автоматную грамматику
можно преобразовать к эквивалентной детерминированной.
Следствие: Все автоматные языки детерминированные.
11
12.
Пример преобразованияГрамматика: G3(L) = {∑, N, S, P}
∑ = {a, b}, N = {S, T, C}, S = {S},
P = {S → aT, S → aC, T → aT, T → aC, T → bC, C → bC, C → b}.
Замена: C → b на C → bZ, добавление: Z → ┴
Недетерминированности:
{S → aT, S → aC}, D = {T, C}
{T → aT, T → aC}, то же самое,
{C → bC, C → bZ}, E = {C, Z}. Здесь E – заключительный
нетерминал.
Преобразованные правила:
P ={S → aD, D → aD, D → bE, T → aD, T → bC, C → bE, E → bE,
Z → ┴, E → ┴}
Преобразованные правила без лишних правил:
P = {S → aD, D → aD, D → bE, E → bE, E → ┴},
Так как нетерминалы Т и С не смогут появиться при любом
12
порождении, начиная с начального нетерминала S.
13.
После преобразования в грамматике могут появитьсябесполезные порождающие правила и бесполезные
нетерминалы. Они не влияют на процесс порождения (и,
соответственно, на процесс распознавания), поэтому их
можно удалить, не изменяя сам язык.
Алгоритм 1. Обнаружение бесполезных нетерминалов 1 типа
(таких, которые не могут быть порождены, начиная с
начального нетерминала).
1. Начальный нетерминал помечается как «полезный».
2. Просматриваются все порождающие правила, у которых в
левой части имеются нетерминалы, помеченные как
«полезные». Нетерминалы в правых частях таких правил
также помечаются как «полезные».
3. 2-й шаг повторяется до тех пор, пока не останется
непросмотренных правил.
4. Нетерминалы, не помеченные как «полезные», считаются
бесполезными.
13
14.
Алгоритм 2. Обнаружение бесполезных нетерминалов 2 типа(таких, из которых не может быть порождена терминальная
цепочка).
1. Просматриваются все порождающие правила, у которых в
правой части имеются только терминалы. Нетерминалы в
левых частях таких правил помечаются как «полезные».
2. Просматриваются все порождающие правила, у которых в
правой части имеются нетерминалы, помеченные как
«полезные». Нетерминалы в левых частях таких правил также
помечаются как «полезные».
3. 2-й шаг повторяется до тех пор, пока не останется
непросмотренных правил.
4. Нетерминалы, не помеченные как «полезные», считаются
бесполезными.
После завершения обоих алгоритмов из грамматики необходимо
удалить все бесполезные нетерминалы и все порождающие
правила, где встречаются эти нетерминалы (как в левой, так и
в правой части).
14
15.
Автоматный язык с несколькими видамицепочек и с символом «┴»
Дана автоматная грамматика, порождающая цепочки нескольких
видов, в конце цепочки имеется символ «┴». Для каждого вида
цепочек предусмотрен отдельный заключительный нетерминал.
Виды цепочек:
• имена (идентификаторы языков программирования);
• целые числа без знака;
• числа с десятичной точкой без знака.
Для сокращения записи вместо отдельных цифр 0,1,. . .,9 будем
писать <ц>, а вместо отдельных букв A,B,. . .,Z будем писать <б>.
Символ «точка» запишем в кавычках: «.».
Правила грамматики (различные правые части при одинаковой
левой части разделены вертикальной чертой):
{S → <б>I | <ц>C, I → <б>I | <ц>I | ┴, C → <ц>C | «.»D | ┴ ,
D → <ц>E,
E → <ц>E | ┴}.
Заключительные нетерминалы: I, C, E.
15
16.
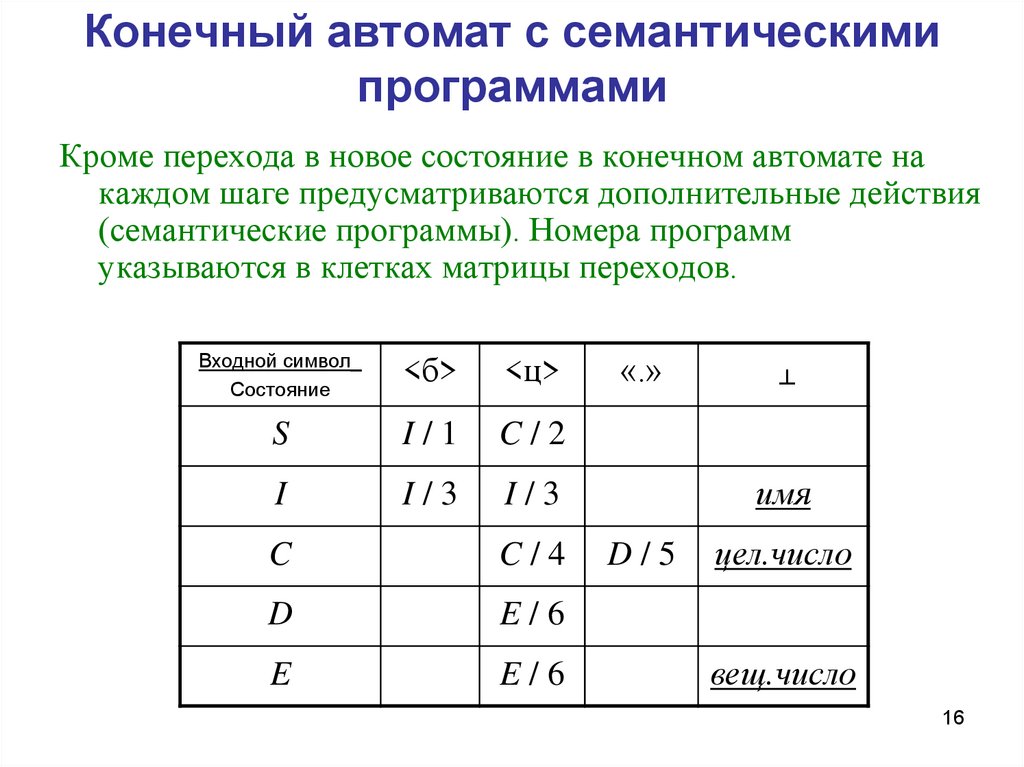
Конечный автомат с семантическимипрограммами
Кроме перехода в новое состояние в конечном автомате на
каждом шаге предусматриваются дополнительные действия
(семантические программы). Номера программ
указываются в клетках матрицы переходов.
Входной символ_
Состояние
<б>
<ц>
S
I/1
C/2
I
I/3
I/3
C
C/4
D
E/6
E
E/6
«.»
┴
имя
D/5
цел.число
вещ.число
16
17.
Семантические программыC[i] – текущий входной символ; name – символьная
строка; n – целочисленная переменная; x, d –
вещественные переменные.
1. name := C[i];
2. n := ord(C[i]) – ord(’0’) ;
3. name := name + C[i];
4. n := n * 10 + ord(C[i]) – ord(’0’);
5. d := 1; x := n;
6. d := d * 0.1; x := x + (ord(C[i]) – ord(’0’)) * d;
17
18.
Лексический анализатор для языкапрограммирования
Лексемы, выделяемые лексическим анализатором:
• имена (идентификаторы),
• ключевые (служебные) слова,
• целые числа,
• вещественные числа (с десятичной точкой и/или с
показателем степени),
• символьные строки,
• составные символы (:= и др.),
• отдельные символы (скобки, знаки операций из одного
символа и т.п.).
Лексемы, пропускаемые лексическим анализатором:
• пробелы и символы конца строки,
• комментарии.
18
19.
Лексический анализатор реализуется как процедура,вызываемая всякий раз, как требуется из входной строки
символов выделить очередную лексему.
Пример входа:
C – входная строка символов.
i – номер текущего входного символа в строке C, с него
начинается анализ; после окончания анализа i – номер
входного символа после лексемы.
Пример выхода:
a – номер распознанной лексемы.
name – символьная строка, содержащая имя, если лексема –
имя или строка символов.
n – значение целого числа, если лексема – целое число.
x – значение вещественного числа, если лексема –
вещественное число.
19
20.
Пример. Анализируемая входная строка символов содержитлексемы:
• имена (идентификаторы),
• служебные слова,
• целые числа без знака,
• числа с десятичной точкой без знака,
• символьные строки в одиночных кавычках,
• отдельные символы языка (такие, как +, *, скобки и др.),
• составной символ (:=),
• пробелы, переводы строк (должны пропускаться) ,
• комментарии, начало - символы (/*), конец - символы (*/)
(должны пропускаться),
• концевой ограничитель - символ (┴),
• все другие символы, которые могут встречаться внутри
комментария (не символы языка).
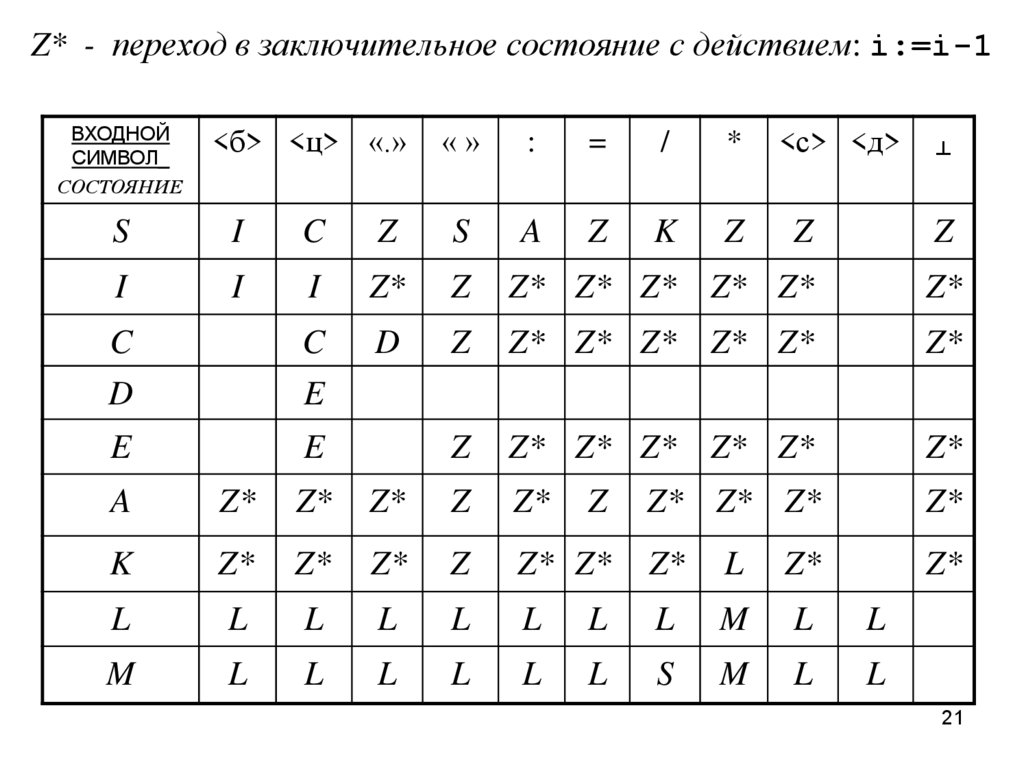
Обозначения входных символов: <ц> – цифра, <б> – буква,
«.» – точка, « » – пробел, <с> – отдельные символы, ┴ –
концевой ограничитель, <д> – другие символы (не символы
20
языка).
21.
Z* - переход в заключительное состояние с действием: i:=i-1ВХОДНОЙ
СИМВОЛ_
СОСТОЯНИЕ
<б> <ц> «.»
«»
:
=
/
*
<с> <д>
S
I
C
Z
S
A
Z
K
Z
Z
Z
I
I
I
Z*
Z
Z* Z* Z* Z* Z*
Z*
C
D
C
E
D
Z
Z* Z* Z* Z* Z*
Z*
E
E
Z
Z* Z* Z* Z* Z*
Z*
Z* Z* Z*
Z*
Z*
A
Z*
Z*
Z*
Z
Z*
Z
K
Z*
Z*
Z*
Z
Z* Z*
Z*
L
Z*
L
L
L
L
L
L
L
L
M
L
L
M
L
L
L
L
L
L
S
M
L
L
┴
21
22.
ПРАВОЛИНЕЙНЫЕ ГРАММАТИКИОбобщение автоматных грамматик. Порождающие
правила в виде:
A → ωB или A → ω
где A, В – нетерминалы, ω – терминальная цепочка,
допустимо: ω = λ.
Пример праволинейной грамматики
Грамматика: G4(L) = {∑, N, S, P}
∑ = {a, b}, N = {S, T, C},
S = {S},
P = {S → aaT, T → aT, T → bbC, T → C, C → a}.
Процесс порождения:
S => aaT => aaC => aaa,
S => aaT => aabbC => aabba,
S => aaT => aaaT => aaaC => aaaa,
S => aaT => aaaT => aaabbC => aabba, . . .
22
23.
Преобразование праволинейной грамматикик автоматной грамматике
1. Пусть в грамматике имеется правило:
A → a1a2. . .anB,
где n > 1.
(*)
Добавим в грамматику новые нетерминалы:
B1, B2, . . . , Bn-1
И вместо правила (*) добавим правила:
A → a1B1, B1 → a2B2, . . . , Bn-1 → anB
23
24.
2. Пусть в грамматике имеется правило:A → B,
(**)
а также правила: B → β1, B → β2, . . . , B → βm,
Вместо правила (**) добавим правила:
A → β1, A → β2, . . . , A → βm
3. Пусть в грамматике имеется правило:
A → λ,
(***)
а также правила: B1 → ω1 A, B2 → ω2 A, . . . , Bk → ωkA,
Вместо правила (***) добавим правила:
B1 → ω1 , B2 → ω2 , . . . , Bk → ωk,
4. Пусть в грамматике имеется правило:
S → λ,
(****)
где S – начальный нетерминал.
Это порождающее правило оставляем без изменения.
24
25.
В результате преобразований язык не изменится.Трудоёмкость преобразования определяется
количеством новых нетерминалов.
Если в языке не было правила S → λ и оно не
появилось после всех преобразований, то
получившаяся грамматика будет автоматной.
Теорема.
Любая праволинейная грамматика эквивалентна автоматной грамматике, к которой
(возможно) добавлено порождающее правило:
S → λ.
Следствие: множество праволинейных языков
почти совпадает с множеством автоматных
языков.
25
26.
Пример преобразованияправолинейной грамматики
Грамматика:
G4(L) = {∑, N, S, P},
∑ = {a, b}, N = {S, T, C},
S = {S},
P = {S → aaT, T → aT, T → bbC, T → C, C → a}.
Автоматная грамматика: G5(L) = {∑, N, S, P},
∑ = {a, b}, N = {S, T, A, B, C},
S = {S},
P = {S → aA, A → aT, T → aT, T → bB, T → a,
B → bC, C → a}.
26
27.
Регулярные множестваРегулярные множества – это следующие множества цепочек
символов из некоторого алфавита Σ:
• Пустое множество Ø.
• Множество из пустой цепочки {λ}.
• Множество из любого символа {a} алфавита Σ.
• Множество всех возможных цепочек вида αβ (конкатенация);
α Є A, β Є B, где A, B – регулярные множества.
• Объединение множеств A U B, где A, B – регулярные
множества.
• Объединение множеств всех возможных цепочек вида
λ, α1, α1α2, α1α2α3, . . . и т.д., где все α1, α2, α3, . . . принадлежат
регулярному множеству A (A* – транзитивное замыкание A ).
27
28.
Регулярные выраженияРегулярное выражение – это шаблон для задания регулярного
множества цепочек символов из некоторого алфавита Σ.
Кроме символов алфавита Σ в регулярное выражение могут входить
вспомогательные метасимволы: Ø (пустое множество), λ (пустая
строка), скобки { }, скобки { }*, вертикальная черта |.
• Пустое множество обозначается знаком Ø.
• Пустая цепочка обозначается знаком λ.
• Символ алфавита Σ обозначает себя сам.
• Если α и β – оба регулярные выражения, то запись вида αβ –
регулярное выражение, конкатенация цепочек из α и β ;
• Если α и β – оба регулярные выражения, то запись вида α | β –
регулярное выражение, обозначающее объединение множеств
цепочек из α и β ;
• Если α – регулярное выражения, то запись вида {α} – то же самое
регулярное выражение, рассматриваемое, как единое целое;
• Если α – регулярное выражения, то запись вида {α}* – регулярное
выражение, обозначающее объединение множеств цепочек из:
λ, α, αα, ααα, . . .
и т.д., ({α}* – транзитивное замыкание α).
28
29.
Примеры1. Регулярное выражение:
{λ|+|–}{0|1|2|3|4|5|6|7|8|9}{0|1|2|3|4|5|6|7|8|9}*
задает запись целого числа без знака или со знаком «+» или «–».
____________________________________________________________________________________________________________________________________
Для краткости вместо явного перечисления цифр или букв через
символ «|», будем использовать многоточие.
____________________________________________________________________________________________________________________________________
2. Регулярное выражение:
{0|1|. . . |9}{0|1|. . . |9}* .{0|1|. . . |9}{0|1|. . . |9}*
задает запись беззнакового десятичного числа с дробной частью.
____________________________________________________________________________________________________________________________________
3. Регулярное выражение:
{A|B|. . .|Z}{0|1|. . . |9|A|B|. . .|Z}*
задает запись идентификатора (имени) для языка
программирования.
29
30.
Преобразование регулярного выражения кправолинейной грамматике
1. Пусть задано регулярное выражение α. Запишем прообраз
порождающего правила в виде: S → α, где S – начальный нетерминал.
2. Пусть прообраз порождающего правила имеет вид: A → aβ,
где A – некоторый нетерминал, a – терминал. Заменим это правило на
следующие: A → aB, B → β, где B – новый нетерминал.
3. Пусть прообраз порождающего правила имеет вид:
A → {α1|α2}β, где A – некоторый нетерминал. Заменим это правило на
следующие: A → α1β, A → α2β.
4. Пусть прообраз порождающего правила имеет вид:
A → {α}*β, где A – некоторый нетерминал. Заменим это правило на
два прообраза: 1) A → β, 2) A → α A.
Преобразования проводятся до тех пор, пока все полученные
порождающие правила не станут праволинейными.
Регулярные множества есть множество автоматных языков!
30
31.
Примеры преобразованияРегулярное выражение:
{λ|+|–}{0|1| . . . |9}{0|1| . . . |9}*
преобразуется в праволинейную грамматику с правилами:
{S → T, S → –T, S → +T, T → <ц>C, C → <ц>C, C → λ}.
Регулярное выражение:
{0|1| . . . |9}{0|1| . . . |9}*.{0|1| . . . |9}{0|1| . . . |9}*
преобразуется в праволинейную грамматику с правилами:
{S → <ц>T, T → <ц>T, T → «.»C, C → <ц>D, D → λ, D → <ц>D}.
Регулярное выражение:
{A|B| . . . |Z}{0|1| . . . |9|A|B| . . . |Z}*
преобразуется в праволинейную грамматику с правилами:
{S → <б>I, I → <б>I, I → <ц>I, I → λ}.
31





























 Программирование
Программирование








