Похожие презентации:
Основы алгебры логики
1.
Основы алгебры логикиШабалдина Н. В.
2.
Отцом алгебры логики по праву считаетсяанглийский математик XIX столетия
Джордж Буль (1815 – 1864).
В его честь алгебра логики названа булевой
алгеброй высказываний
Алгебра логики изучает строение (форму структуру)
сложных логических высказываний и способы
установления их истинности с помощью
алгебраических методов.
3.
Логическое высказывание – это повествовательноепредложение, про которое однозначно можно
сказать: истинно оно или ложно
Будут ли высказыванием следующие предложения?
Пятью пять – двадцать пять.
Пекин – столица Японии.
Информатика – любимый предмет.
Х+3=5
Победа!
Который час?
Ты сегодня пойдёшь в школу?
4.
Составное высказывание – логическая функция, которая содержитнесколько простых мыслей, соединенных между собой с помощью
логических операций. Символическое обозначение – F(A,B,…).
Логические операции – логическое действие
Если составное высказывание (логическую функцию)
выразить в виде формулы, в которую войдут
логические переменные и знаки логических операций,
то получится логическое выражение, значение
которого можно вычислить.
Значением логического выражения могут быть только
ИСТИНА (1) или ЛОЖЬ (0).
5.
Простые высказыванияА={Луна – планета};
В={2*2=4};
Любое высказывание либо истинно (1), либо ложно (0)
6.
Составные высказыванияА={Луна – планета};
В={2*2=4};
А или В - Луна – планета или 2*2=4;
А и В - Луна – планета и 2*2=4;
не А и не В - Луна не планета и 2*2не равно 4;
7.
Таблицы истинности – таблицы, в которых по действиямпоказано, какие значения принимает логическое выражение
при всех возможных наборах его переменных
Причем, количество строк в таблице истинности
вычисляется как 2n, где n – количество переменных, а
количество столбцов = количество переменных +
количество логических операций.
8.
Алгоритм построения таблицы истинности1.
2.
3.
4.
N - количество переменных.
M - количество операций.
Число столбцов = (N+M).
Число строк =2N.
9.
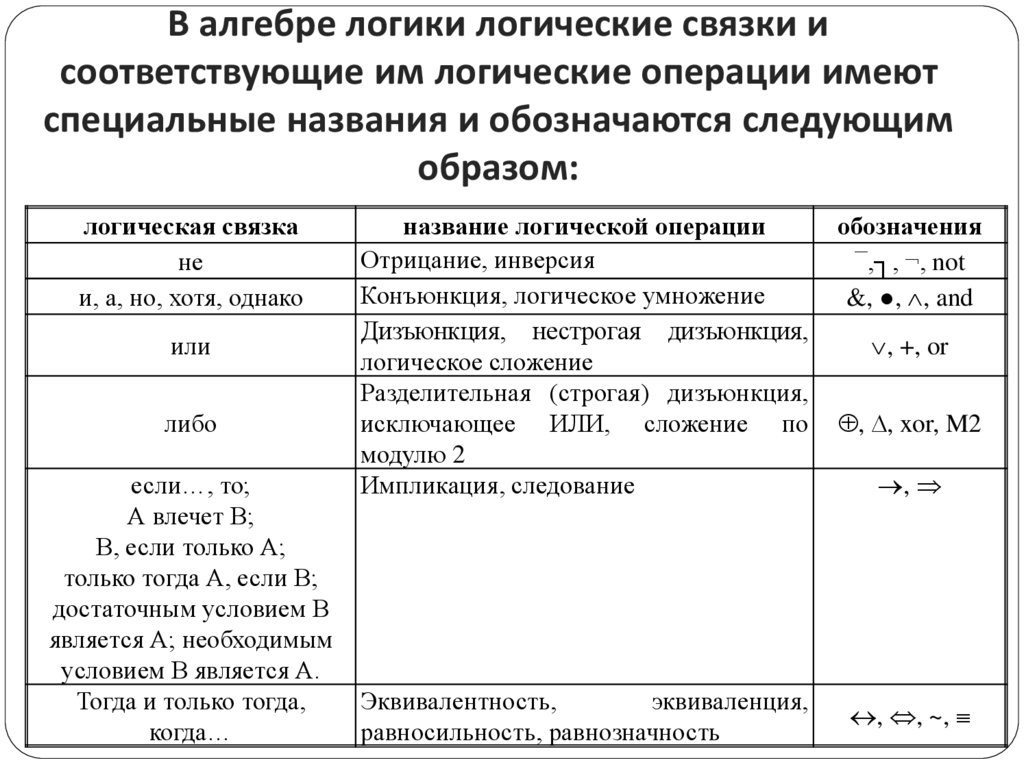
В алгебре логики логические связки исоответствующие им логические операции имеют
специальные названия и обозначаются следующим
образом:
логическая связка
не
и, а, но, хотя, однако
или
либо
если…, то;
А влечет В;
В, если только А;
только тогда А, если В;
достаточным условием В
является А; необходимым
условием В является А.
Тогда и только тогда,
когда…
название логической операции
Отрицание, инверсия
Конъюнкция, логическое умножение
Дизъюнкция, нестрогая дизъюнкция,
логическое сложение
Разделительная (строгая) дизъюнкция,
исключающее ИЛИ, сложение по
модулю 2
Импликация, следование
обозначения
¯,┐, ¬, not
&, ●, , and
Эквивалентность,
эквиваленция,
равносильность, равнозначность
, , ~,
, +, or
, , xor, M2
,
10.
Конъюнкция (логическое умножение) – это логическаяоперация, ставящая в соответствие каждым двум
простым высказываниям составное высказывание,
являющееся истинным тогда и только тогда, когда оба
исходных высказывания истинны.
Таблица
Диаграмма
истинности
Эйлера – Венна
А
B A&B
0
0
0
0
1
0
1
0
0
1
1
1
11.
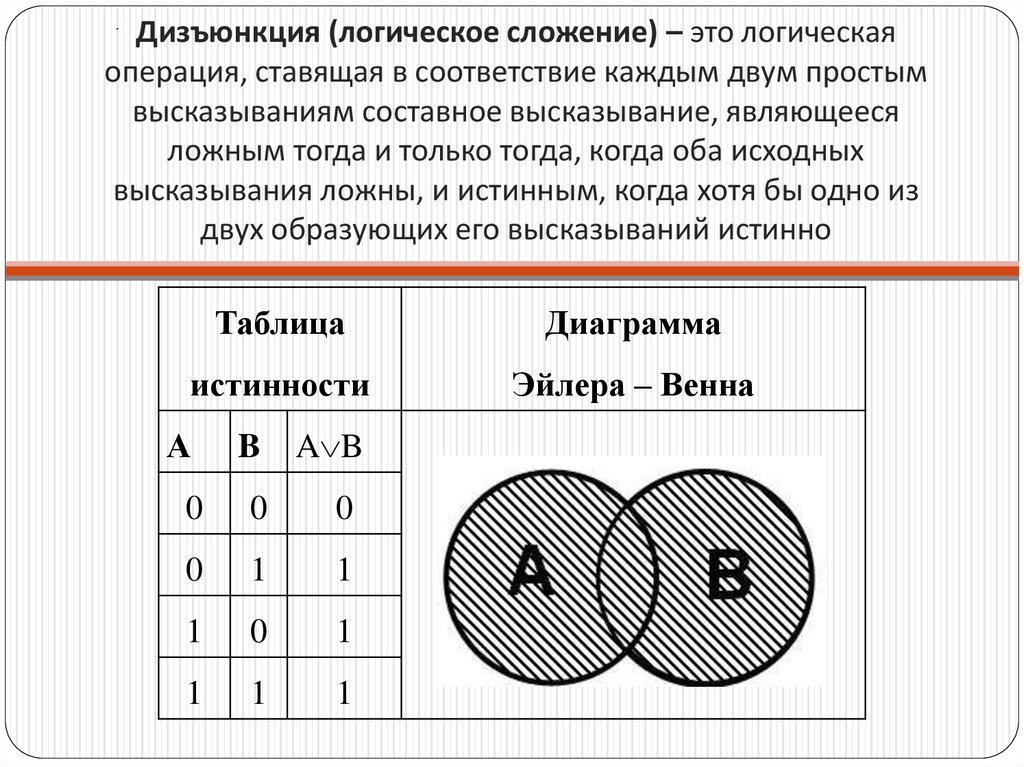
Дизъюнкция (логическое сложение) – это логическаяоперация, ставящая в соответствие каждым двум простым
высказываниям составное высказывание, являющееся
ложным тогда и только тогда, когда оба исходных
высказывания ложны, и истинным, когда хотя бы одно из
двух образующих его высказываний истинно
Таблица
Диаграмма
истинности
Эйлера – Венна
А
B A B
0
0
0
0
1
1
1
0
1
1
1
1
12.
Инверсия (отрицание) – это логическая операция,которая каждому простому высказыванию ставит в
соответствие составное высказывание,
заключающееся в том, что исходное высказывание
отрицается.
Таблица
Диаграмма
истинности
Эйлера – Венна
А
А
0
1
1
0
13.
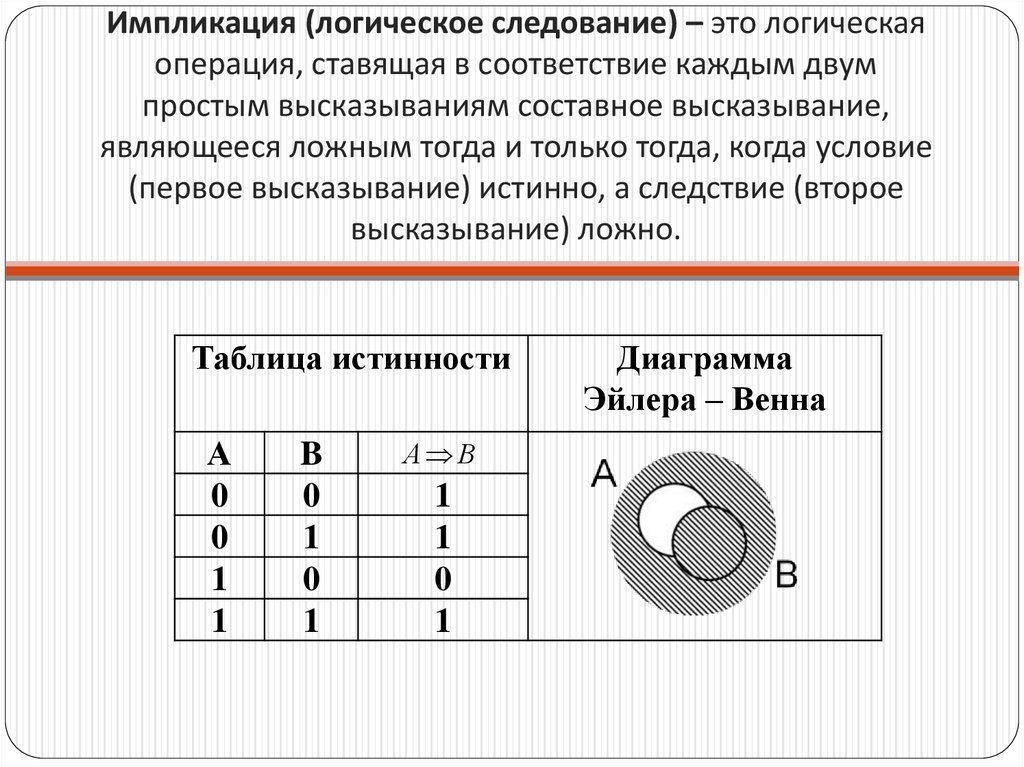
Импликация (логическое следование) – это логическаяоперация, ставящая в соответствие каждым двум
простым высказываниям составное высказывание,
являющееся ложным тогда и только тогда, когда условие
(первое высказывание) истинно, а следствие (второе
высказывание) ложно.
Таблица истинности
А
0
0
1
1
B
0
1
0
1
А В
1
1
0
1
Диаграмма
Эйлера – Венна
14.
Свойства импликацииA 0 A
A A 1
0 A 1
1 A A
15.
Эквиваленция (равнозначность) – это логическаяоперация, ставящая в соответствие каждым двум
простым высказываниям составное высказывание,
являющееся истинным тогда и только тогда, когда оба
исходных высказывания одновременно истинны или
одновременно ложны.
Таблица истинности
Диаграмма
Эйлера – Венна
А В
А
B
0
0
1
0
1
0
1
0
0
1
1
1
16.
Свойства эквивалентности:A A 0
A A 1
A 0 A
A 1 A
17.
Строгая или разделительная дизъюнкция(исключающее ИЛИ, сложение по модулю 2) – это
логическая операция, ставящая в соответствие каждым
двум простым высказываниям составное высказывание,
являющееся истинным тогда и только тогда, когда ровно
одно из исходных высказываний является истинным.
Таблица истинности
Диаграмма
Эйлера – Венна
А В
А
B
0
0
0
0
1
1
1
0
1
1
1
0
18.
Свойства строгой дизъюнкции:A A 1
A A 0
A 0 A
A 1 A
19.
Стрелка Пирса (символ Лукашевича, ИЛИ-НЕ) – этологическая операция, ставящая в соответствие каждым
двум простым высказываниям составное высказывание,
являющееся истинным тогда и только тогда, когда оба
высказывания ложны. Соответствует обороту речи
«ни…,ни…».
Таблица истинности
А В
А
B
0
0
1
0
1
0
1
0
0
1
1
0
Обозначается:
A В А В
20.
Стрелка Пирса обладает тем свойством, что через нееодну выражаются все другие логические операции.
Например:
А A А
А & B A А B B
А B A B A B
21.
Свойства Стрелки Пирса:A A 0
A A A
A 0 A
A 1 0
22.
Штрих Шеффера (И-НЕ) – это логическая операция,ставящая в соответствие каждым двум простым
высказываниям составное высказывание, являющееся
ложным тогда и только тогда, когда оба высказывания
истинны. Соответствует обороту речи «не…или не…».
Таблица истинности
Обозначается:
АВ
А
B
0
0
1
0
1
1
1
0
1
1
1
0
AВ А& В
23.
Штрих Шеффера как и стрелка Пирса обладает.
тем свойством,
что через нее одну выражаются все
другие логические операции.
Например:
А AА
А & B А B A В
А B A А В B
24.
;;
;
.
Свойства штриха Шеффера:
A A 1
AA A
A0 1
A1 А
25.
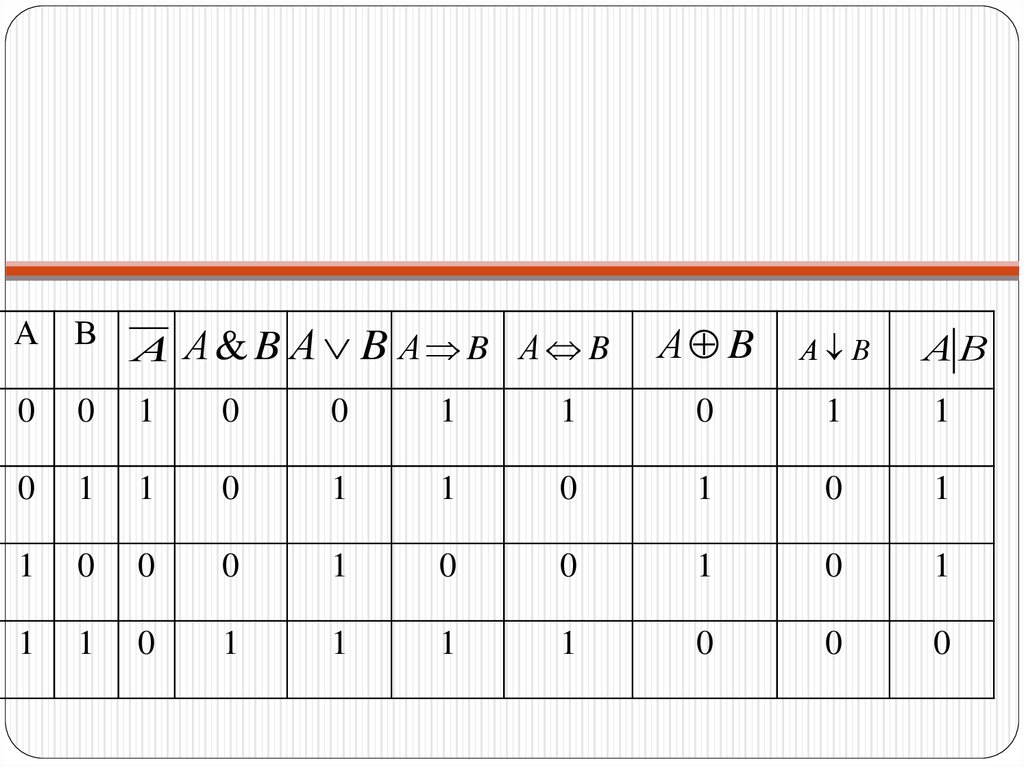
АВ
А А& B А B А B А B
0
0
1
0
0
1
0
1
1
0
1
1
0
0
0
1
1
0
1
А B
А В
1
0
1
1
1
0
1
0
1
1
0
0
1
0
1
1
1
1
0
0
0
АВ
26.
При составлении логического выражениянеобходимо учитывать порядок выполнения
логических операций:
•Действия в скобках;
•Инверсия;
•Конъюнкция;
• Дизъюнкция (строгая и нестрогая);
• Импликация;
•Эквивалентность.
27.
Основные операции: и, или, неА В B A
A B A B
A B A& B A& B
A B ( A B) & ( B A)
A B ( A B) ( A B)
А В А B & B A
А В A B
28.
A B B AAB BA
A ( B С ) ( A B) AC
A ( B С ) AB AC
29.
Законы логикиЗакон
переместительный
распределительный
Сочетательный
Идемпотенции
Поглощения
Операция с
инверсией
Операция с
константами
Для или
Для и
A B B A
AB BA
A (B С) A B A C
A B С ( A B) ( A C )
A ( B С ) ( A B) AC
A ( B С ) ( A B) AC
A A A
A A В A
A А 1
A 0 А
A 1 1
A A A
A ( A В) A
A А 0
A 0 0
A 1 А
30.
Законы для отрицанияЗакон
Правило де Моргана
Для или
Для и
A B A B
Двойное отрицание
А А
A B A B
31.
Закон исключения (склеивания)( A B) ( А B) В
A B А B В
32.
Иногда при решении задач полезныформулы де Моргана:
¬ (A B) = ¬ A ¬ B
¬ (A B) = ¬ A ¬ B
A B A B
A B A B
Огастес (Август) де Морган – шотландский математик и логик.
33.
1. Является ли данная функциятождественно-истинной?
( A C ) (C A B)
Способы решения:
Упрощение функции
Построение таблицы истинности
34.
( A C ) (C A B)( A C ) (C A B )
( A C ) (C A B )
( A C ) ( A C ) (C A B )
( A C ) ( A C) C ( A B )
C
(A C ) C (A B)
A C
C A (A B) A B C
A B
1 способ
35.
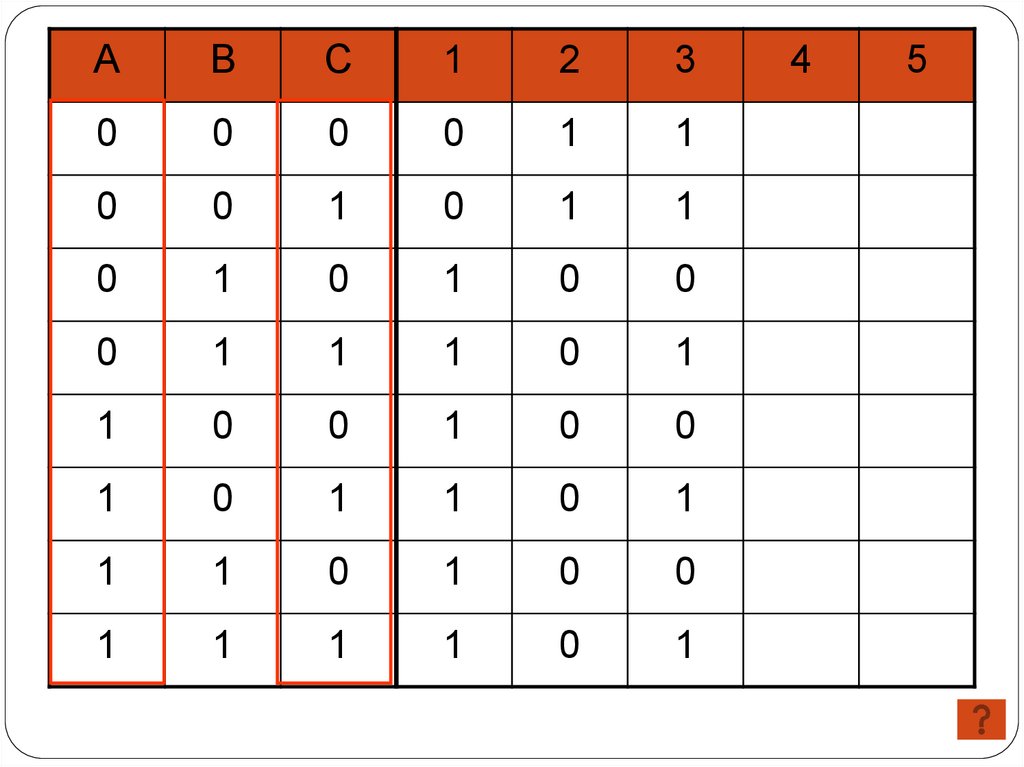
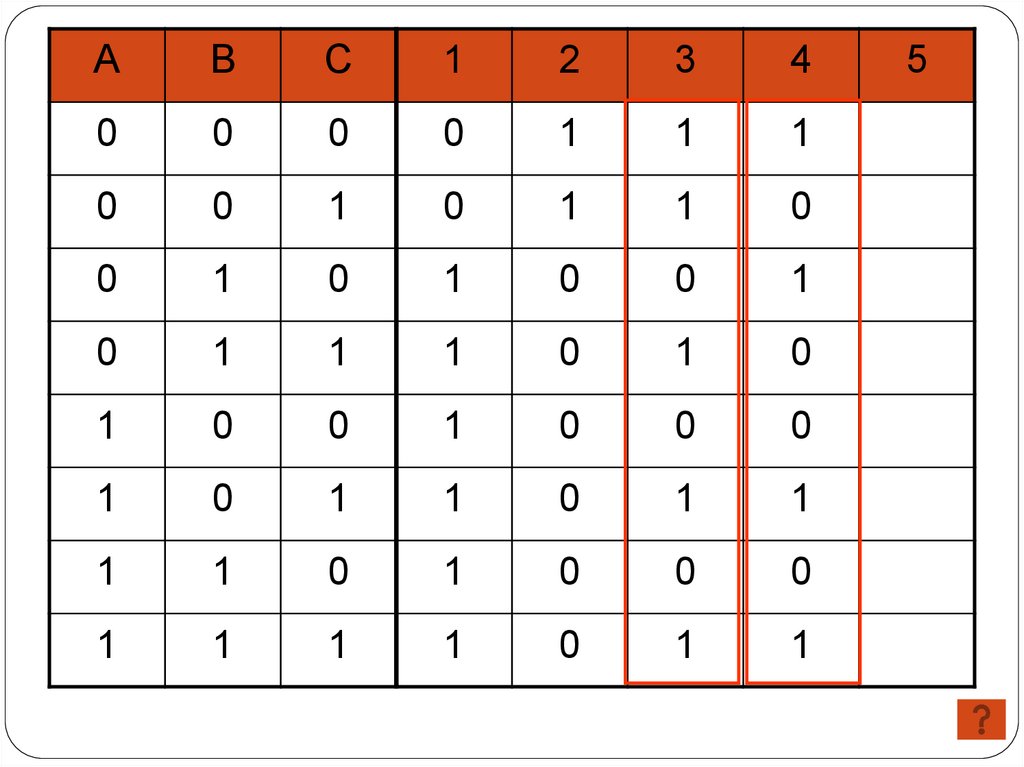
2 способ4
5
3
2
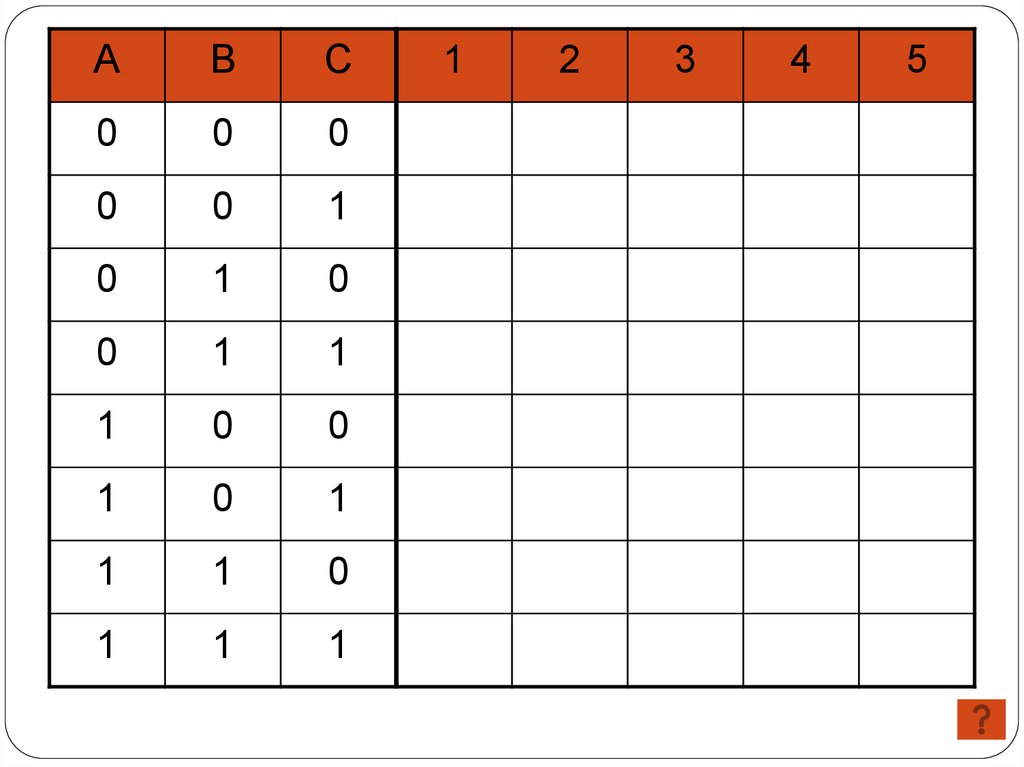
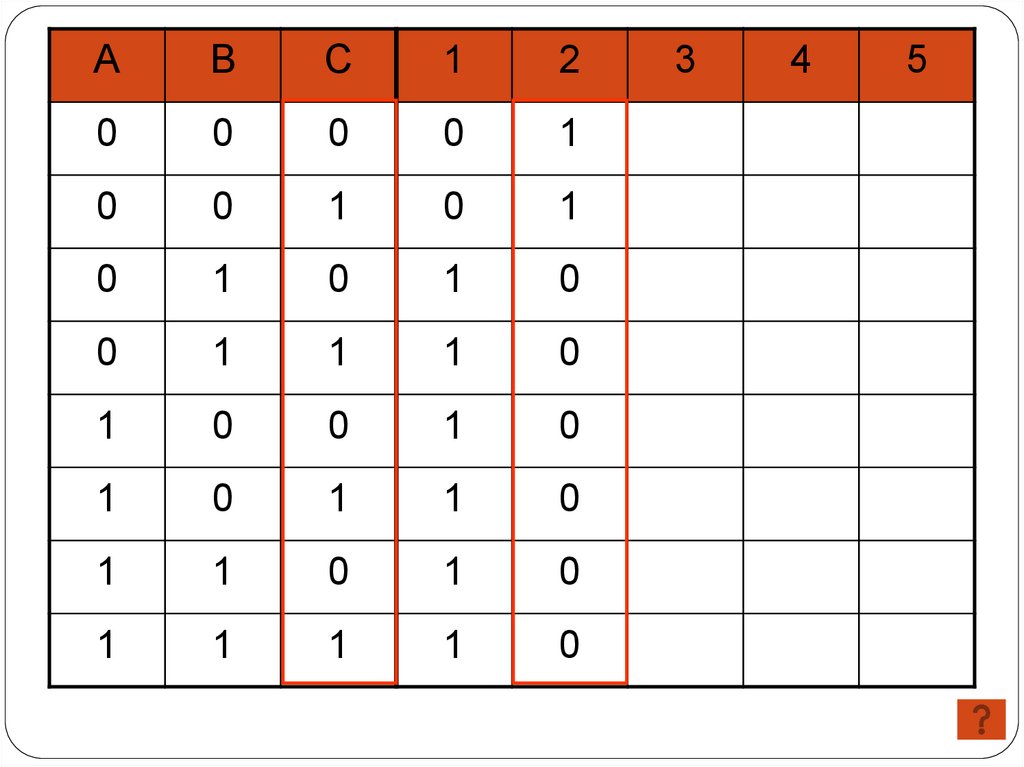
( A C ) (C A B)
1
36.
AB
C
0
0
0
0
0
1
0
1
0
0
1
1
1
0
0
1
0
1
1
1
0
1
1
1
1
2
3
4
5
37.
AB
C
1
0
0
0
0
0
0
1
0
0
1
0
1
0
1
1
1
1
0
0
1
1
0
1
1
1
1
0
1
1
1
1
1
2
3
4
5
38.
AB
C
1
2
0
0
0
0
1
0
0
1
0
1
0
1
0
1
0
0
1
1
1
0
1
0
0
1
0
1
0
1
1
0
1
1
0
1
0
1
1
1
1
0
3
4
5
39.
AB
C
1
2
3
0
0
0
0
1
1
0
0
1
0
1
1
0
1
0
1
0
0
0
1
1
1
0
1
1
0
0
1
0
0
1
0
1
1
0
1
1
1
0
1
0
0
1
1
1
1
0
1
4
5
40.
AB
C
1
2
3
4
0
0
0
0
1
1
1
0
0
1
0
1
1
0
0
1
0
1
0
0
1
0
1
1
1
0
1
0
1
0
0
1
0
0
0
1
0
1
1
0
1
1
1
1
0
1
0
0
0
1
1
1
1
0
1
1
5
41.
AB
C
1
2
3
4
5
0
0
0
0
1
1
1
1
0
0
1
0
1
1
0
1
0
1
0
1
0
0
1
0
0
1
1
1
0
1
0
1
1
0
0
1
0
0
0
1
1
0
1
1
0
1
1
1
1
1
0
1
0
0
0
1
1
1
1
1
0
1
1
1
42.
2. Следующие два высказывания истинны:«неверно, что если магазин А организует
распродажу, то магазин С тоже»;
«из двух магазинов В и С организует распродажу
только один».
Какие магазины организуют распродажу?
43.
«Если магазин А организует распродажу, томагазин С тоже»
A→C
«Неверно, что если магазин А организует
распродажу, то магазин С тоже»
A C
Из условия известно, что это высказывание
истинно. Следовательно:
A C 1
44.
«Из двух магазинов В и С организует распродажутолько один»
B C 1
45.
( A C )( B C ) 1( A C )(( BC ) ( B C ))
AC (( BC ) ( B C ))
C ABC 1
AC B
AC BC
0
Это возможно только в одном случае, когда A=1,
B=1, С=0.
То есть, магазины A и B проводят распродажу, а
магазин С – нет.
46.
3. На олимпиаде по информатике студенты A, B, C и Dзаняли первые четыре места. Когда их спросили
о распределении мест, они дали три ответа: D –
первый или B – второй; C – первый или A –
четвертый; D – второй или B – третий. Как
распределились места, если в каждом ответе
только одно утверждение истинно?
47.
D – первый или B – второй: D1 B2=1C – первый или A – четвертый: C1 A4=1
D – второй или B – третий: D2 B3=1
(D1 B2)(C1 A4)(D2 B3)=1
(D1C1 B2C1 D1A4 B2A4)(D2 B3)=1
B2C1D2 D1A4D2 B2A4D2 B2C1B3 D1A4B3 B2A4B3=1
D1A4B3=1
Следовательно, D – первый, С – второй,
B – третий, A – четвертый.
48.
3. Сформулируйте на естественном языке отрицаниеследующего высказывания:
"Виктор пойдет на рыбалку только при солнечной
погоде, если не будет жарко".
49.
«Виктор пойдет на рыбалку» - A«Будет солнечная погода» - B
«Будет жарко» - C
Перефразируем высказывание:
«Если будет солнечная погода
и не будет жарко, то Виктор пойдет на рыбалку».
Тогда исходное высказывание имеет вид:
BC A
50.
BC A BC AB C A
Будет солнечная погода и нежарко, а Виктор
не пойдет на рыбалку.
51.
Дизъюнктивно-нормальная формаДНФ — является логической суммой
элементарных конъюнкций.
Совершенная ДНФ – логическая сумма
элементарных конъюнкций, в каждой из
которых присутствуют все переменные данной
функции.
52.
Конъюнктивно-нормальная формаКНФ — является логическим произведением
элементарных дизъюнкций.
Совершенная КНФ – логическое произведение
элементарных дизъюнкций, в каждой из
которых присутствуют все переменные данной
функции.
53.
Табличный способ приведения кСДНФ
Составляем таблицу истинности данной
функции.
Рассматриваем только те строки таблицы, в
которых функция принимает значение 1.
Каждой такой строке соответствует
конъюнкция всех аргументов (без
повторений). Причем аргумент,
принимающий значение 0, входит в нее с
отрицанием; значение 1 – без отрицания.
Наконец, образуем дизъюнкцию всех
полученных конъюнкций.
54.
Табличный способ приведения кСКНФ
Составляем таблицу истинности данной
функции.
Рассматриваем только те строки таблицы, в
которых функция принимает значение 0.
Каждой такой строке соответствует
дизъюнкция всех аргументов (без
повторений). Причем аргумент,
принимающий значение 0, входит в нее без
отрицания; значение 1 – с отрицанием.
Наконец, образуем конъюнкцию всех
полученных дизъюнкций.
55.
Если условится из двух форм, СДНФ и СКНФ,отдавать предпочтение той, которая содержит
меньше букв, то
СДНФ предпочтительней, если в столбце значений
функции таблицы истинности меньше единиц;
СКНФ – если в этом столбце меньше нулей.
56.
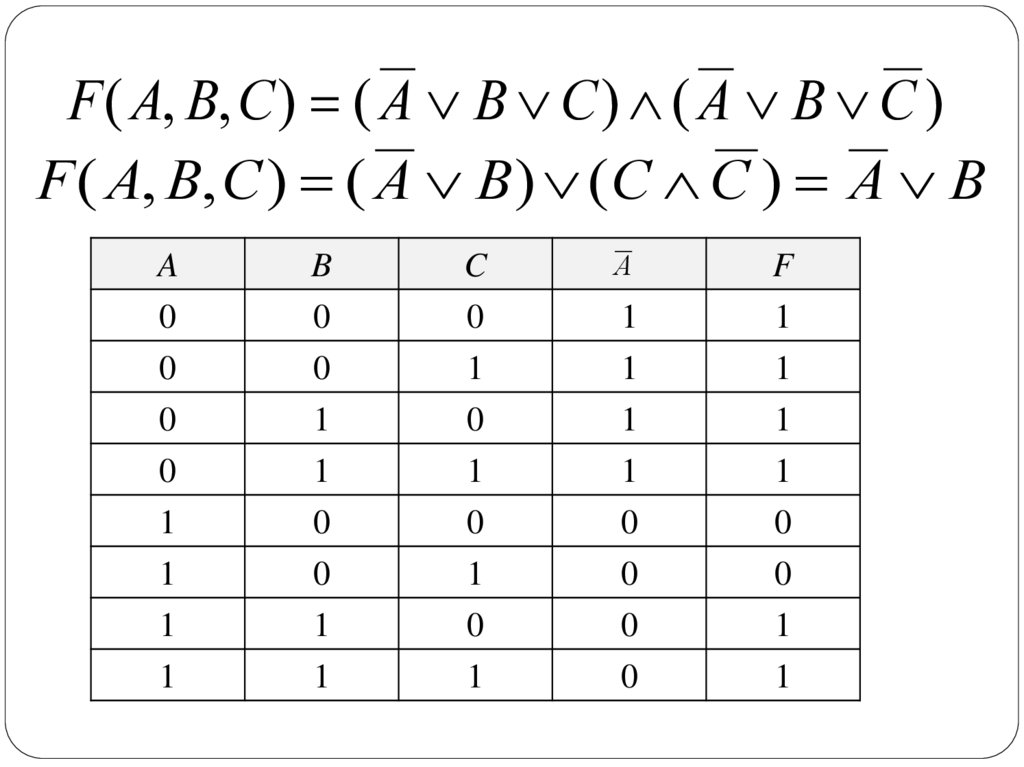
Дана таблица истинности логической функции оттрех переменных. Построить логическую формулу,
реализующую эту функцию.
A
B
C
F(A, B, C)
0
0
0
1
0
0
1
1
0
1
0
1
0
1
1
1
1
0
0
0
1
0
1
0
1
1
0
1
1
1
1
1
57.
F ( A, B, C ) ( A B C ) ( A B C )F ( A, B, C ) ( A B ) ( C C ) A B
A
0
B
0
C
0
A
1
F
1
0
0
1
1
1
0
0
1
1
0
1
1
1
1
1
1
1
1
0
0
1
0
1
0
0
0
0
0
0
1
1
1
1
0
1
58.
4. Построить схему электрической цепидля подъезда трехэтажного здания, чтобы
выключателем на любом этаже можно было бы
включить и выключить свет во всем подъезде.
59.
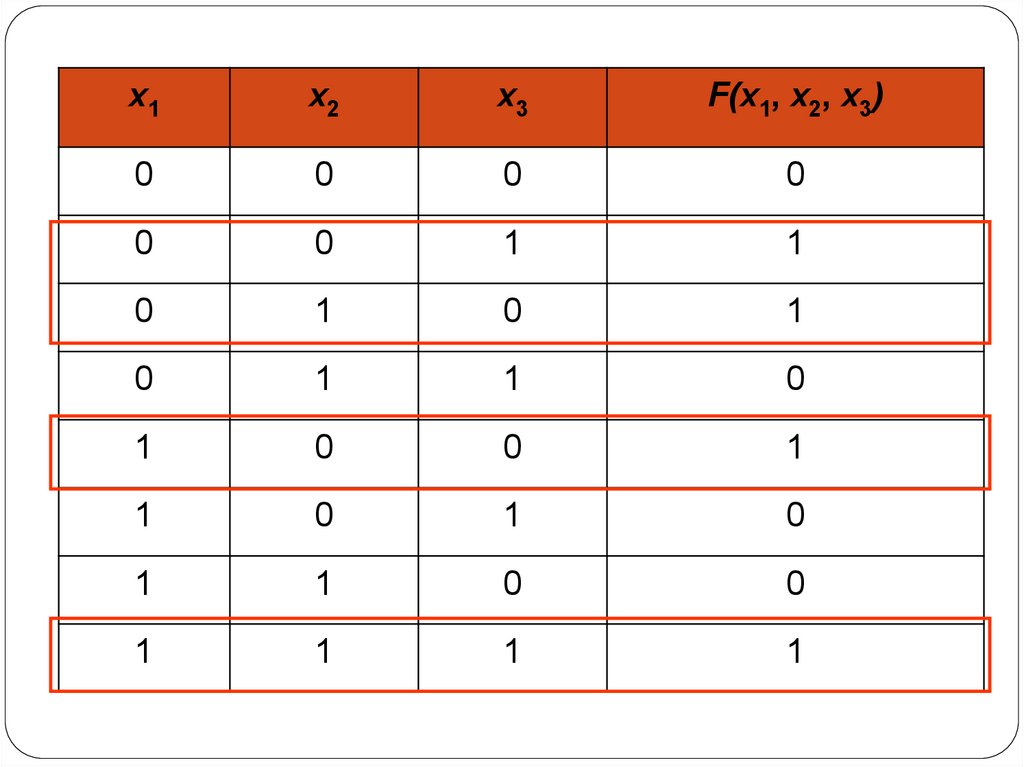
Сначала построим таблицу истинности длятребуемой функции.
Переменными функции будут выключатели на
каждом этаже подъезда.
Свет будет включаться при условии, что во
включенном состоянии находятся нечетное
количество выключателей.
Свет будет выключен, если во включенном
состоянии будут четное количество выключателей
или ни одного.
60.
x1x2
x3
F(x1, x2, x3)
0
0
0
0
0
0
1
1
0
1
0
1
0
1
1
0
1
0
0
1
1
0
1
0
1
1
0
0
1
1
1
1
61.
Теперь по таблице истинности построимдизъюнктивно-нормальную форму.
Отберем те строки в таблице истинности, которые в
результате дают единицу.
Для каждой строки строится конъюнкция всех
переменных.
Если переменная в этой строке равна нулю, то она
берется с отрицанием, если единице – без
отрицания.
Затем соединим все полученные конъюнкции
операциями дизъюнкции.
62.
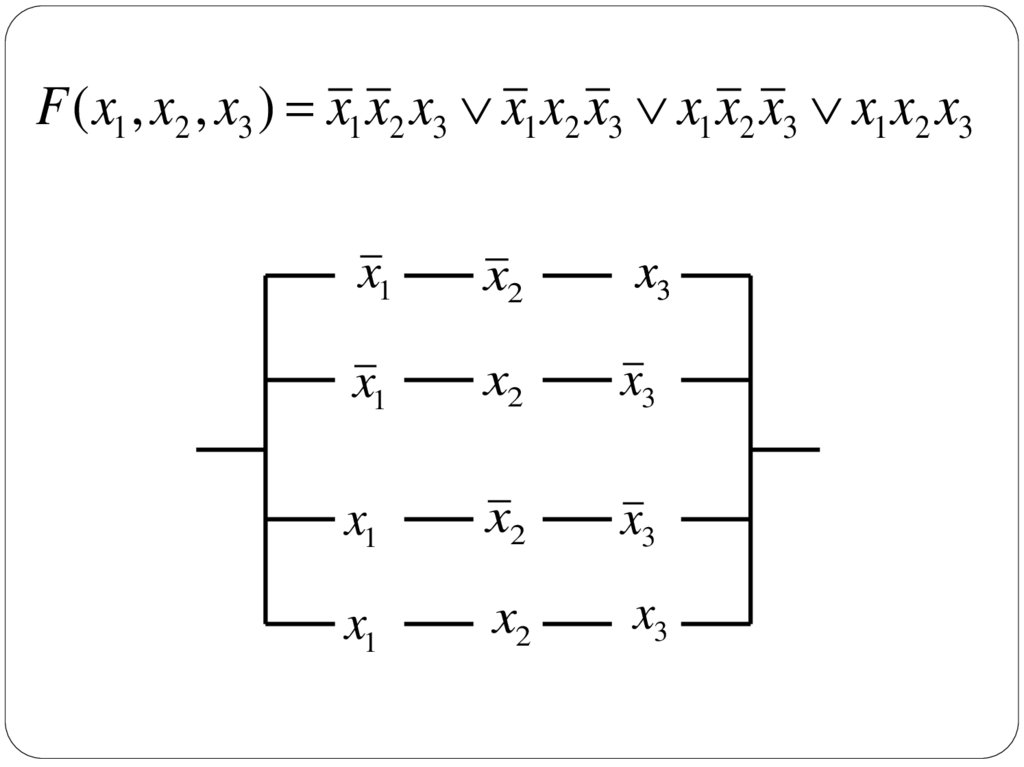
F ( x1 , x2 , x3 ) x1 x2 x3 x1 x2 x3 x1 x2 x3 x1 x2 x3x1
x2
x1
x2
x3
x1
x2
x3
x1
x2
x3
x3
63.
5. После традиционного вечера встречи с выпускникамишколы в стенгазете появилась заметка о трех наших
бывших учениках. В ней было сказано, что Иван,
Андрей и Борис стали учителями. Теперь они
преподают разные дисциплины: один из них –
математику, второй – физику, а третий – химию.
Живут они тоже в разных городах: Минске, Витебске,
Харькове. В заметке было также написано, что их
первоначальные планы осуществились не
полностью:
Иван живет не в Минске.
Андрей – не в Витебске.
Житель Минска преподает не математику.
Андрей преподает не физику.
Повезло только жителю Витебска: он преподает любимую
им химию.
Можно ли по этим данным определить, кто где живет и
что преподает?
64.
Алгоритм решения задач на приведениемножеств во взаимно-однозначное
соответствие
1.
2.
3.
4.
5.
6.
Строится пространственная система координат XYZ, на осях
проставляются названия множеств и элементы этих множеств.
Читается условие задачи. Если пара элементов в двух
множествах находится в соответствии, то точка, лежащая на
пересечении соответствующих прямых становится центром
темного кружка, в противном случае – белого кружка.
Применяется правило экстраполяции.
Применяется правило проектирования.
Повторять шаги 3)-4) пока это возможно.
Если в сложившейся ситуации возможности экстраполяции и
проектирования исчерпаны, а задача не решена, то делается
допущение о цвете фигуры в какой-либо свободной вершине
сетки. В случае противоречия допущение отклоняется цвет
фигуры в данной точке меняется на противоположный.
65.
Правила экстраполяции вплоскости
«Темная» экстраполяция. Если на горизонтали
(вертикали) все фигуры, кроме одной, светлы, то
свободная занимается темной фигурой.
«Светлая» экстраполяция. Если на горизонтали
(вертикали) имеется «темная» фигура, то все
фигуры на ней – светлые.
Множественная экстраполяция. Если две (n)
параллели в плоскости одинаково светло
раскрашены везде за исключением двух (n)
неокрашенных вершин, то на двух (n) параллелях
другого направления, проходящих через эти
вершины вне данных прямых вставляются
светлые фигуры.
66.
Правило множественногопроектирования
«Темная» фигура в своей плоскости
проектируется на координатные оси. Прямые,
проведенные через проекции в двух других
плоскостях, раскрашиваются одинаково.
67.
ПредметФ
Х
М
И
М
В
Х
Город
А
Б
Имена
68.
Иван преподает химию и живет в Витебске.Андрей преподает математику и живет в Харькове.
Борис преподает физику и живет в Минске.























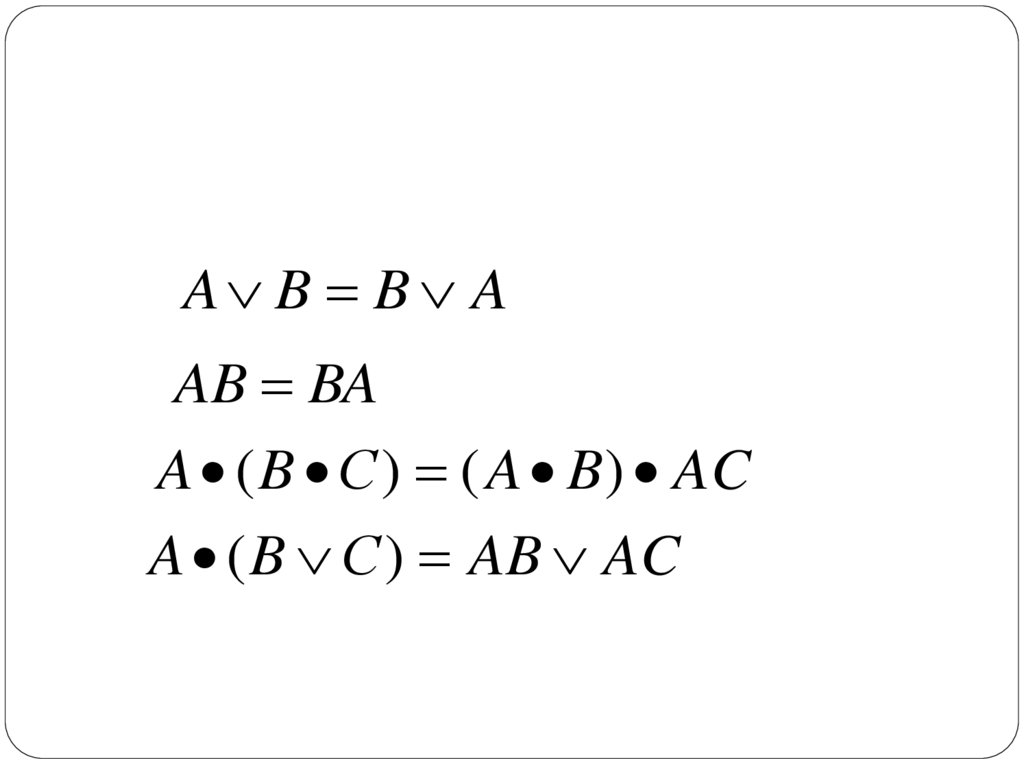

































 Математика
Математика