Похожие презентации:
КЕГЭ по информатике 2023. Решение заданий №3 и №14
1.
Решение заданий №3 и №14КЕГЭ по информатике 2023
Подготовил: учитель информатики МБОУ СШ № 3 гог Выкса
Гусева Марина Валентиновна
2.
Задание № 3Базовый уровень
Время выполнения – 3 минуты
3.
Задание № 3Демонстрационный
вариант ЕГЭ 2023
4.
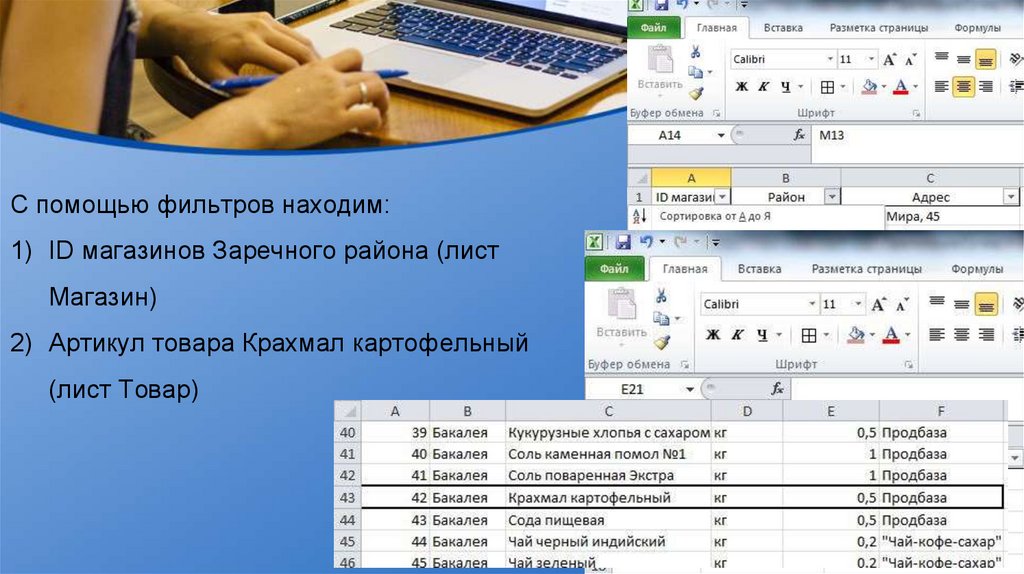
С помощью фильтров находим:1) ID магазинов Заречного района (лист
Магазин)
2) Артикул товара Крахмал картофельный
(лист Товар)
5.
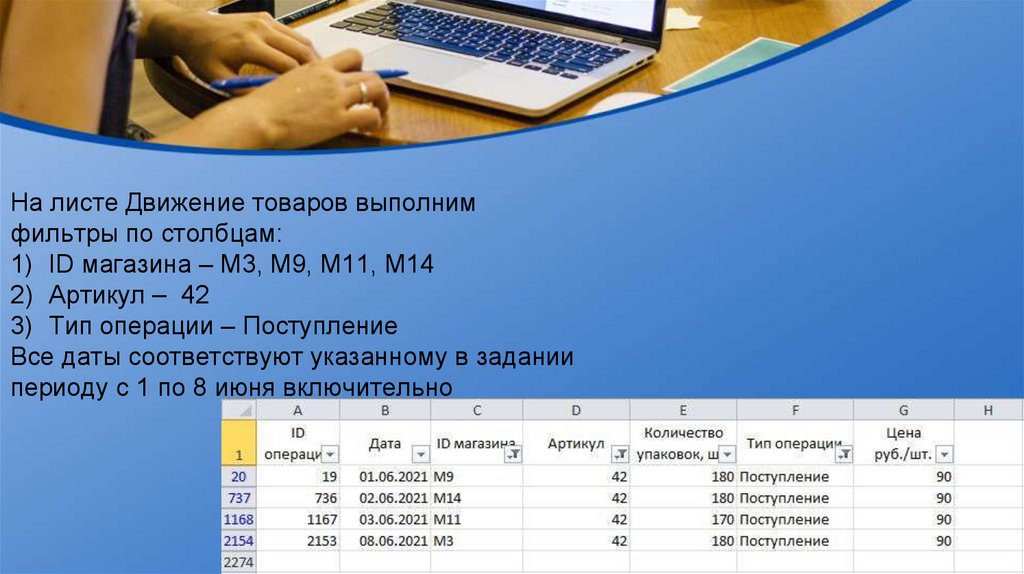
На листе Движение товаров выполнимфильтры по столбцам:
1) ID магазина – М3, М9, М11, М14
2) Артикул – 42
3) Тип операции – Поступление
Все даты соответствуют указанному в задании
периоду с 1 по 8 июня включительно
6.
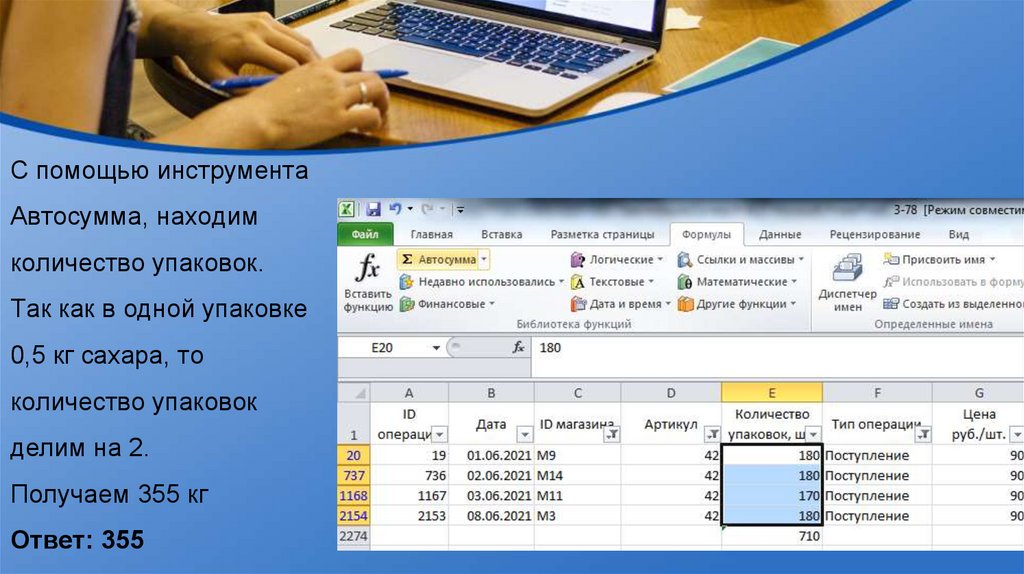
С помощью инструментаАвтосумма, находим
количество упаковок.
Так как в одной упаковке
0,5 кг сахара, то
количество упаковок
делим на 2.
Получаем 355 кг
Ответ: 355
7.
Движение товаровЗадание № 3
Досрочный этап
ЕГЭ 2022
ID операции
Дата
ID магазина
Артикул
Тип операции
Количество упаковок
Магазин
ID
Район
Адрес
Товар
Артикул
Отдел
Наименование
Единица измерения
Количество в упаковке
Производитель
Используя информацию из базы данных в файле 3-78.xls, определите на
сколько увеличилось количество упаковок яиц диетических, имеющихся в
наличии в магазинах Заречного района, за период с 1 по 5 июня
включительно.
8.
С помощью фильтров находим:1) ID магазинов Заречного района (лист
Магазин)
2) Артикул товара Яйцо диетическое (лист
Товар)
9.
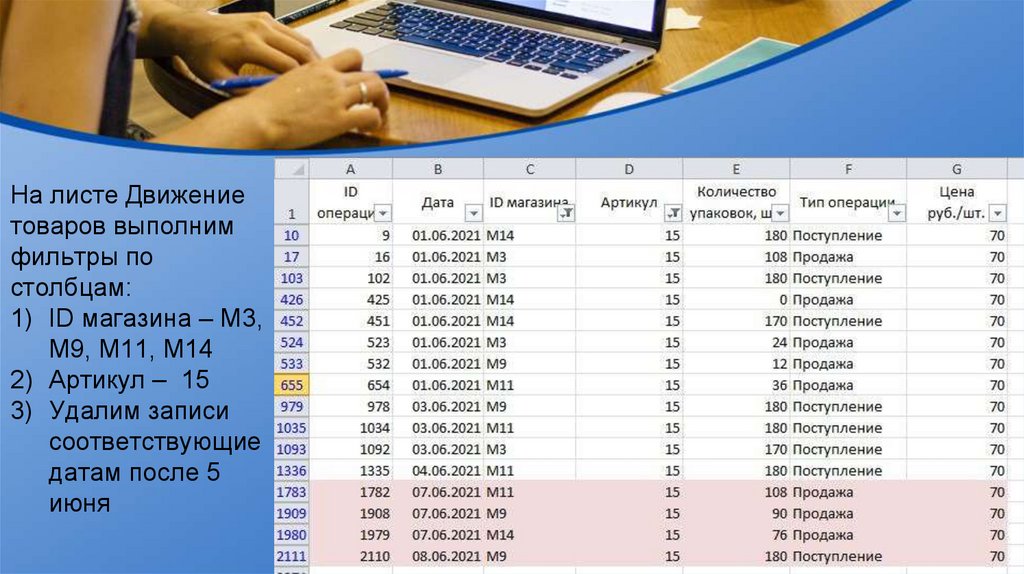
На листе Движениетоваров выполним
фильтры по
столбцам:
1) ID магазина – М3,
М9, М11, М14
2) Артикул – 15
3) Удалим записи
соответствующие
датам после 5
июня
10.
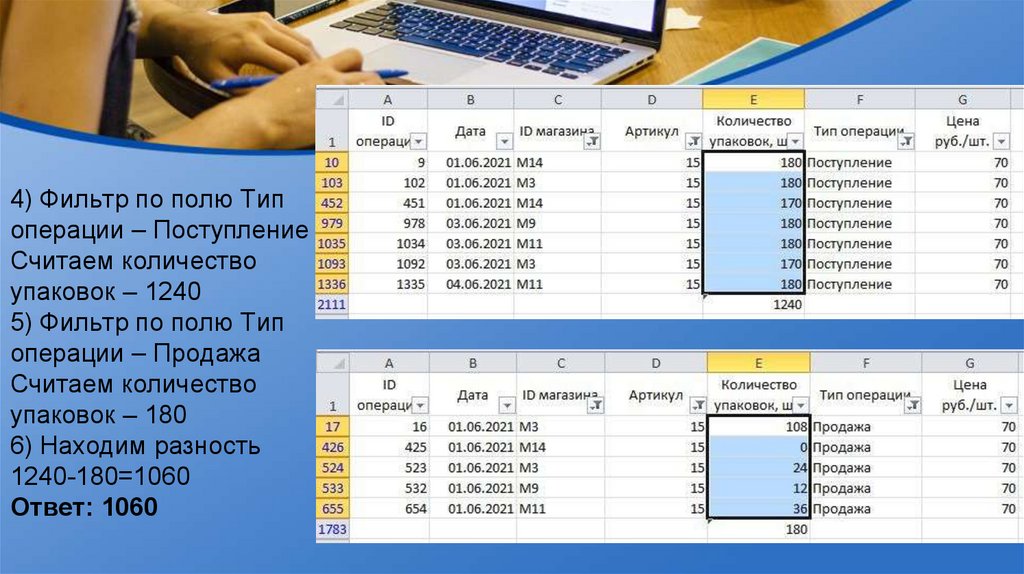
4) Фильтр по полю Типоперации – Поступление
Считаем количество
упаковок – 1240
5) Фильтр по полю Тип
операции – Продажа
Считаем количество
упаковок – 180
6) Находим разность
1240-180=1060
Ответ: 1060
11.
Движение товаровЗадание № 3
ЕГЭ 2022
ID операции
Дата
ID магазина
Артикул
Тип операции
Количество упаковок
Магазин
ID
Район
Адрес
Товар
Артикул
Отдел
Наименование
Единица измерения
Количество в упаковке
Производитель
Используя информацию из базы данных в файле 3-0.xls, определите, на
сколько увеличилось количество упаковок всех видов макарон производителя
«Макаронная фабрика», имеющихся в наличии в магазинах Первомайского
района, за период с 1 по 8 июня включительно.
12.
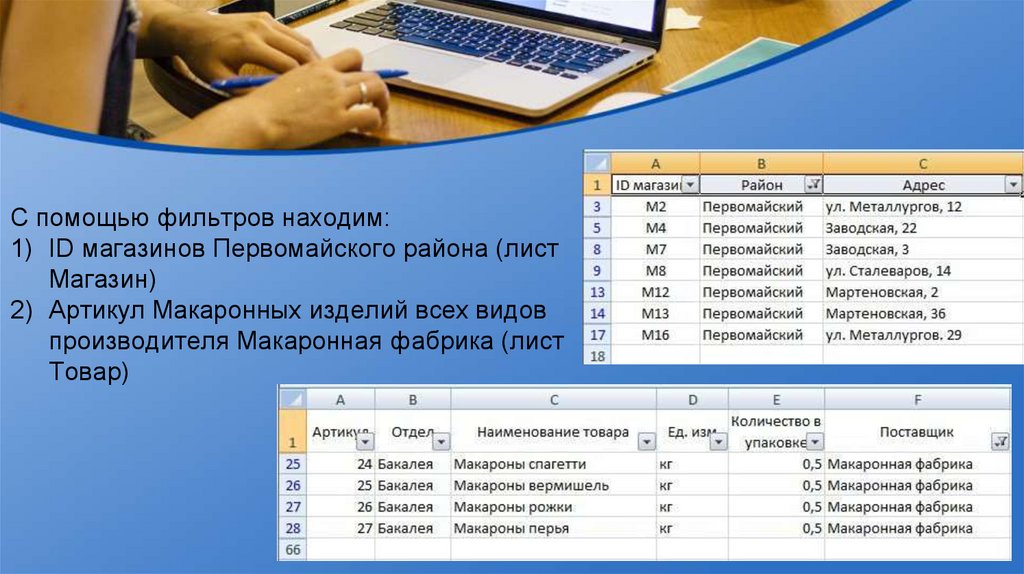
С помощью фильтров находим:1) ID магазинов Первомайского района (лист
Магазин)
2) Артикул Макаронных изделий всех видов
производителя Макаронная фабрика (лист
Товар)
13.
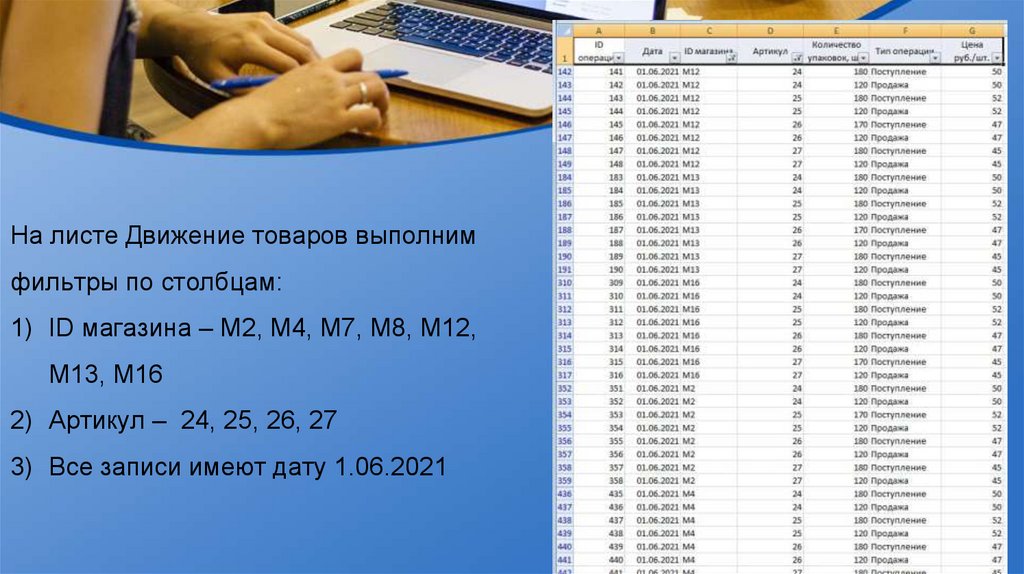
На листе Движение товаров выполнимфильтры по столбцам:
1) ID магазина – М2, М4, М7, М8, М12,
М13, М16
2) Артикул – 24, 25, 26, 27
3) Все записи имеют дату 1.06.2021
14.
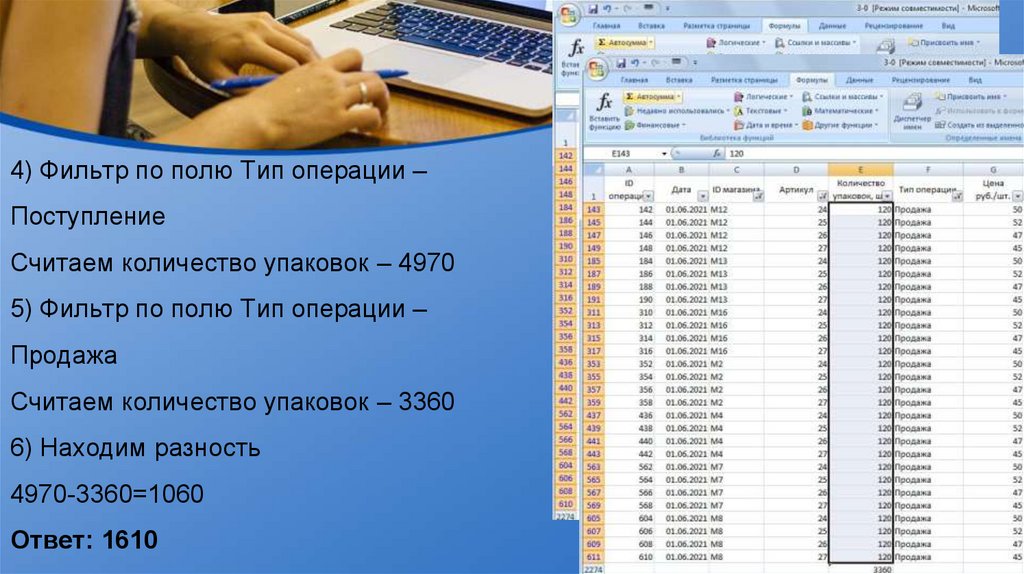
4) Фильтр по полю Тип операции –Поступление
Считаем количество упаковок – 4970
5) Фильтр по полю Тип операции –
Продажа
Считаем количество упаковок – 3360
6) Находим разность
4970-3360=1060
Ответ: 1610
15.
Задание № 14Повышенный уровень
Время выполнения – 3 минуты
16.
Задание № 14Демонстрационный
вариант ЕГЭ 2023
17.
Что нужно знать:• принципы кодирования чисел в позиционных системах счисления
• чтобы перевести число, скажем, 12345N, из системы счисления с
основанием N в десятичную систему, нужно умножить значение каждой
цифры на N в степени, равной ее разряду:
4 3 2 1 0 ← разряды
• 1 2 3 4 5N = 1·N4 + 2·N3 + 3·N2 + 4·N1 + 5·N0
18.
Запишем оба слагаемых в развернутой форме в системе счисления соснованием 15:
123x515 + 1x23315 =
(1·154+2·153+3·152+x·15+5) + (1·154+x·153+2·152+3·15+3) =
=(2·154+2·153+5·152+ 3·15+8) + (x·153 +x·15)=
= (101250 + 6750 + 1125 + 45 + 8) + x · (3375 + 15) = 109178 + 3390·x
Вычисления удобно выполнять в электронных таблицах
19.
Нам нужно, чтобы выражение Y = 109178 + 3390·x делилось на 14.Остаток от деления 109178 на 14 равен 6;
остаток от деления 3390 на 14 равен 2.
Для того чтобы Y делилось на 14, остаток от деления Y на 14 должен быть
равен 0 (14, 28 и т.д.)
Попробуем сложить остатки.
Уравнение 6+2*x = 0, даст нам отрицательное значение x, значит нужно
взять следующее значение остатка 6+2*x = 14 <=> 2*x = 8 <=> x =4.
Y = 109178 + 3390·4 = 122738. В качестве ответа нужно поделить Y на 14,
получим 8767
Ответ: 8767.
20.
Задание № 14 (А. Богданов)Операнды арифметического выражения записаны в системе счисления с
основанием 17.
66x63₁₇ – 5x810₁₇
В записи чисел переменной x обозначена неизвестная цифра из алфавита 17ричной системы счисления. Определите наименьшее значение x, при котором
значение данного арифметического выражения кратно 11. Для найденного
значения x вычислите частное от деления значения арифметического
выражения на 11 и укажите его в ответе в десятичной системе счисления.
Основание системы счисления в ответе указывать не нужно.
21.
Запишем оба операнда арифметического выражения в развернутой формев системе счисления с основанием 17:
66x6317 - 5x81017 =
(6·174+6·173+x·172+6·17+3) - (5·174+x·173+8·172+1·17) =
=(174+6·173-8·172+ 5·17+3) + x·(172 -173)= 110775-4624 x
22.
Остаток от деления 110775 на 11 равен 5;остаток от деления 4624 на 11 равен 7.
Для того чтобы наша разность делилась на 11, остаток от деления должен
быть равен 0 (11, 22 и т.д.)
Попробуем сложить остатки.
Уравнения 5+7*x = 0; 5+7*x = 11; 5+7*x = 22 не дадут нам натурального
значения x, значит нужно взять следующее значение остатка
5+7*x = 33 <=> 7*x = 28 <=> x =4.
(110775 - 4624·4)/11 = 8389.
Ответ: 8389
23.
Задание № 14 (А. Богданов)Операнды арифметического уравнения записаны в разных системах
счисления.
3364x₁₁ + x7946₁₂ = 55x87₁₄
В записи чисел переменной x обозначена неизвестная цифра. Определите
наименьшее значение x, при котором данное уравнение обращается в
тождество. В ответе укажите значение правой части уравнения в десятичной
системе счисления. Основание системы счисления в ответе указывать не
нужно.
24.
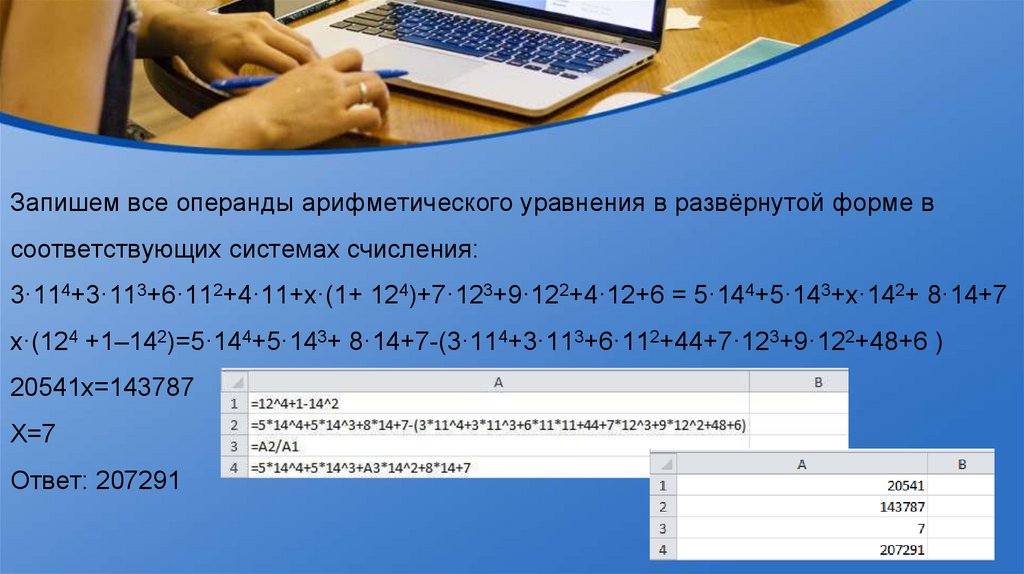
Запишем все операнды арифметического уравнения в развёрнутой форме всоответствующих системах счисления:
3·114+3·113+6·112+4·11+x·(1+ 124)+7·123+9·122+4·12+6 = 5·144+5·143+x·142+ 8·14+7
x·(124 +1–142)=5·144+5·143+ 8·14+7-(3·114+3·113+6·112+44+7·123+9·122+48+6 )
20541x=143787
X=7
Ответ: 207291
25.
Задание № 14 (В. Шубинкин)Операнды арифметического выражения записаны в системах счисления с
основаниями 15 и 17.
123x515 + 67y917
В записи чисел переменными x и y обозначены неизвестные цифры из
алфавитов 15-ричной и 17-ричной систем счисления соответственно.
Определите значения x, y, при которых значение данного арифметического
выражения кратно 131. Для найденных значений x, y вычислите частное от
деления значения арифметического выражения на 131 и укажите его в ответе
в десятичной системе счисления. Если можно выбрать x, y не единственным
образом, возьмите ту пару, в которой значение y меньше. Основание системы
счисления в ответе указывать не нужно.
26.
Запишем все слагаемые в развёрнутой форме в соответствующих системахсчисления: 154+2·153+3·152+x·15+5+6·173+7·172+y·17+9 = 89565+15x+17y
Складываем остатки от деления на 131. Чтобы исходная сумма делилась на 131,
сумма остатков должна быть равна 0, 131, 262, 393…
92+15x+17y=0, (131, 262, 393..)
Очевидно, что уравнение 92+15x+17y=0 натуральных решений не имеет.
Каким способом можно подобрать натуральные x и y удовлетворяющие одному
из уравнений?
27.
Я предлагаю построить матрицу значений в ЭТ.Так как x - это цифра 15 системы счисления, то его значения задаём от 0 до
14, а y – цифра 17 системы счисления, её значение от 0 до 16. В формуле
для вычисления значения суммы используем смешанные ссылки
28.
Будем искать в матрице нужные нам значения: 131, 262, 393, 524Таким образом x=11, y=8
29.
Осталось сосчитать частное от деления значения арифметическоговыражения на 131:
(89565+15∙11+17∙8)/131=686
Ответ: 686
30.
В работе использованыматериалы сайтов:
• https://4ege.ru/informatika/65775demoversija-ege-2023-poinformatike.html
• https://kpolyakov.spb.ru/school/ege
.htm
31.
Спасибо завнимание!






















 Информатика
Информатика








