Задача классическая

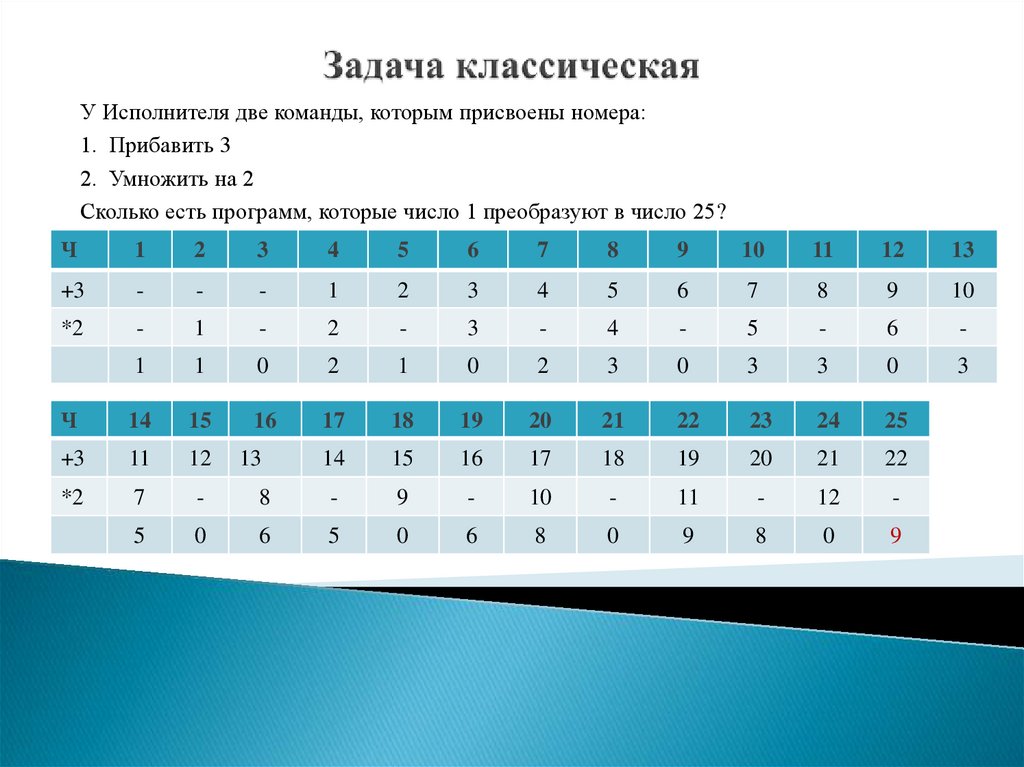
У Исполнителя две команды, которым присвоены номера:
1. Прибавить 3
2. Умножить на 2
Сколько есть программ, которые число 1 преобразуют в число 25?
Ч
1
2
3
4
5
6
7
8
9
10
11
12
13
+3
-
-
-
1
2
3
4
5
6
7
8
9
10
*2
-
1
-
2
-
3
-
4
-
5
-
6
-
1
1
0
2
1
0
2
3
0
3
3
0
3
Ч
14
15
16
17
18
19
20
21
22
23
24
25
+3
11
12
14
15
16
17
18
19
20
21
22
*2
7
-
8
-
9
-
10
-
11
-
12
-
5
0
6
5
0
6
8
0
9
8
0
9
13

3.

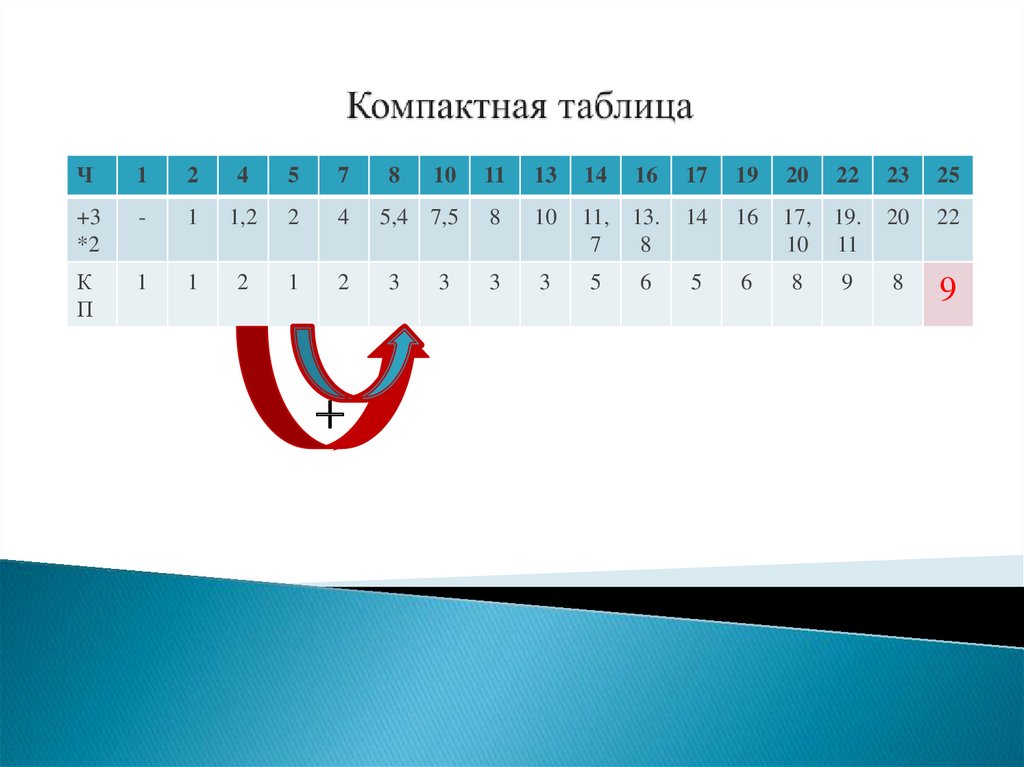
Ч
1
2
4
5
7
+3
*2
-
1
1,2
2
4
К
П
1
1
2
1
2
+
8
10
11
13
14
16
17
19
20
22
23
25
5,4 7,5
8
10
11, 13.
7
8
14
16
17, 19.
10 11
20
22
3
3
5
6
8
9
3
3
5
6
8
9

4.

У Исполнителя две команды, которым присвоены номера:
1. прибавь 1
2. сделай нечётное (2x+1)
Сколько существует таких программ, которые число 1 преобразуют в число 25, причём
траектория вычислений не содержит число 24?
Ч
1
2
3
4
5
6
7
8
9
10
11
12
+1
-
1
2
3
4
5
6
7
8
9
10
11
2х+1
-
-
1
-
2
-
3
-
4
-
5
-
КП
1
1
2
2
3
3
5
5
7
7
10
10
24 -> 25
1 ………………12

5.

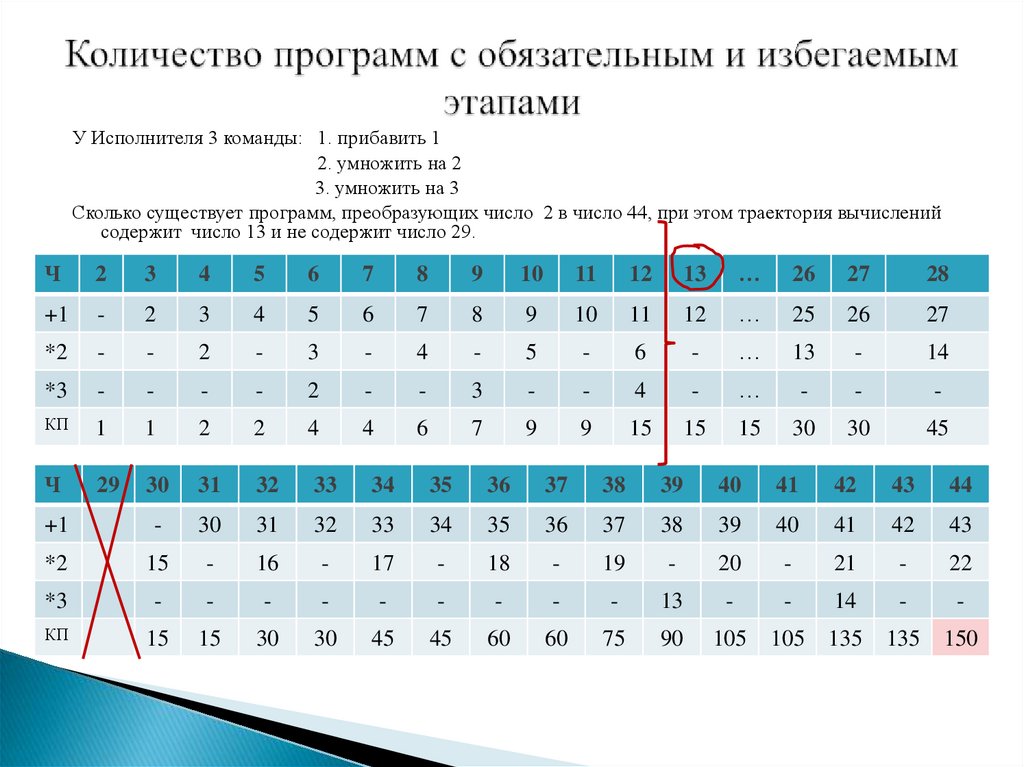
У Исполнителя 3 команды: 1. прибавить 1
2. умножить на 2
3. умножить на 3
Сколько существует программ, преобразующих число 2 в число 44, при этом траектория вычислений
содержит число 13 и не содержит число 29.
Ч
2
3
4
5
6
7
8
9
10
11
12
13
…
26
27
28
+1
-
2
3
4
5
6
7
8
9
10
11
12
…
25
26
27
*2
-
-
2
-
3
-
4
-
5
-
6
-
…
13
-
14
*3
-
-
-
-
2
-
-
3
-
-
4
-
…
-
-
-
КП
1
1
2
2
4
4
6
7
9
9
15
15
15
30
30
45
Ч
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
+1
-
30
31
32
33
34
35
36
37
38
39
40
41
42
43
*2
15
-
16
-
17
-
18
-
19
-
20
-
21
-
22
*3
-
-
-
-
-
-
-
-
-
13
-
-
14
-
-
КП
15
15
30
30
45
45
60
60
75
90
105
105
135
135
150

6.

У исполнителя Калькулятор две команды:
1. прибавь 4,
2. вычти 3.
Сколько различных чисел можно получить из числа 1 с помощью программы, которая содержит ровно 7
команд?
1 1 1 1 1 1 1
2 1 1 1 1 1 1
2 2 1 1 1 1 1
2 2 2 1 1 1 1
2 2 2 2 1 1 1
2 2 2 2 2 1 1
2 2 2 2 2 2 1
2 2 2 2 2 2 2
Всего 8 программ, дающие 8
различных чисел.

7.

У исполнителя есть две команды, которым присвоены номера:
1. Прибавить 1
2. Умножить на 2
Укажите наименьшее натуральное число, которое нельзя получить из исходного числа 1, выполнив
программу исполнителя, содержащую не более четырёх команд.
1
2
3
4
5
8
4
7
12
8
5
6
6
10
9
16

8.

У исполнителя Калькулятор есть три команды, которым присвоены номера:
1. Прибавить 1
2. Прибавить 5
3. Умножить на 3
Сколько программ можно составить из 7 команд при получении числа 27 из числа 3?
start = 3
steps = 7
result = 27
operations = [
lambda x:x+1,
lambda x:x+5,
lambda x:x*3
]
counter = 0
for i1 in range(3):
for i2 in range(3):
for i3 in range(3):
for i4 in range(3):
for i5 in range(3):
for i6 in range(3):
for i7 in range(3):
a=
operations[i7](operations[i6](operations[i5](operations[i4](operations[i3](operations[i2]((operations[i1](start))
))))))
if a == result:
#print(i1,i2,i3,i4,i5,i6,i7)
counter += 1
print(counter)

9.

У исполнителя Калькулятор есть три команды, которым присвоены номера:
1. Прибавить 1
2. Прибавить 5
3. Умножить на 3
Сколько программ можно составить из 7 команд при получении числа 27 из числа 3?
#include <iostream>
#include <vector>
using namespace std;
bool can(int a)
{
}
if(a + 1 == 27)
{
return 1;
}
else if(a + 5 == 27)
{
return 1;
}
else if(a * 3 == 27)
{
return 1;
}
return 0;
int ways(int a, int c)
{
if(c == 7)
{
if(can(a))
{
}
else
{
}
}
}
return 0;
return (ways(a + 1, c+1) + ways(a + 5, c+1) + ways(a * 3, c+1));
int main(int argc, char** argv) {
}
return 1;
std::cout<<ways(3,1);
return 0;

English Русский Правила