27.30M

Категория: $Математика$ Математика

Похожие презентации:

История математики

История математики. Развитие и становление. Возникновение арифметики и геометрии

Математика в истории

Великие математики

История развития математики

История появления математики

Из истории математики

Великие математики

История возникновения и развития математики

История математики

1.

ГПОУ ТО Тульский педагогический колледж
Презентация к индивидуальному проекту
Автор проекта: студентка группы 1 А
Корешкова Александра
Руководитель проекта: Морозова Елена
Константиновна
г. Тула 2023-2024 гг.

2.

3.

Более 4000 лет до нашей эры самой
древней математической
деятельностью был счет.
Он был необходим для
подсчета добычи, для обмена и
для торговли, для учета
поголовья скота.

4.

Племена в разных
уголках мира вели счет
по-разному.
Кто-то сопоставлял
количество предметов с
пальцами рук и ног.
Кто пользовался
камешками или
палочками, в дальнейшем
зарубками или узелками.

5.

Первые клинописные
таблички относятся к 2-му
тыс. до нашей эры.
Математические расчеты
на табличках связаны с
ведением хозяйства,
расчеты за товары,
вычисления процентов,
расчет налогов.

6.

7.

Название периода
Длительность
Начальный период,
или период зарождения
математики
Он продолжался со времени
появления человека разумного и
закончился примерно в VII в. до
н.э.
Период элементарной
математики, или математики
постоянных величин
Он охватывает период с VI в. до
н. э. по XVI в. н.э.
Период математики
переменных величин
В XVII–XVIII веках в Европе
устанавливается новый
общественный строй –
капитализм. Время эпохи научной
революции
Период современной
математики
XIX-XX вв., математика
развивается по разным
направлениям. Появляются новые
области математики

8.

9.

«Папирус Ахмеса», найден в 1858
году египтологом Риндом.
Длина 525 см и ширина 33 см, он
содержит 84 решенные задачи.
Десятичная непозиционная система
счисления. Каждый знак в записи
числа повторяется столько раз,
сколько в данном числе единиц
соответствующего разряда. Записи
выполняются справа налево.
Греческий алфавит состоял из 27
символов. Эти 27 символов
использовались в их истеме
счисления. Позже символы
Vau, Koppa и Sampi, устарели,
они использовались только для
математики. В Греческом
алфавите теперь 24 символа.

10.

Египтяне дроби записывали как
суммы единичных дробей (долей).
Например, вместо 8/15 они писали
1/3 + 1/5. Дробь 7/8 записывали в
виде долей: 1/2 + 1/4 + 1/8.
Египтяне следовали солнечному
календарю, был связан с циклом
разливов Нила и включал в себя три
сезона – разлив, посев, жатву.
В году 365 дней = 360 + 5 священных дней, год поделен на 12 месяцев. 4 месяца
– 1 сезон, 3 сезона – 1 год. 3 недели – 1 месяц, 10 дней – 1 неделя, 24 часа – 1
сутки.

11.

12.

Вавилоняне (шумеры) в математике
писали «тексты» на глиняных
табличках клинописью.
Самая знаменитая математическая
Старовавилонская табличка
Содержит перечень прямоугольных
треугольников с рациональными
сторонами, то есть троек
пифагоровых чисел x2 + y2 = z2 и
свидетельствует о том, что теорема
Пифагора была известна
вавилонянам не менее чем за тысячу
лет до рождения её автора.
Шумерская клинописная табличка.
Записи на клинописных табличках в
основном были связаны с ведением
хозяйства и строительством.

13.

Числа менее 60 обозначались с
помощью двух знаков. Они имели
клинообразный вид и повторялись
нужное число раз.
При вычислениях умножения
вавилоняне пользовались готовыми
таблицами умножения. Так же как
мы пользуемся таблицами
логарифмов.
Шестидесятеричная система вавилонян. В наше время мы так же делим час
на 60 минут, минуту на 60 секунд. Так же, как и вавилоняне, мы делим
окружность на 360 равных частей (градусов).

14.

В случае двух неизвестных одно называлось длиной (х), другое — шириной (у),
их произведение —«площадью»; «полем» или «длиной— шириной»;
говорилось также о «сторонах моих квадратов» (т.е. x2 и y2). При этом в
примерах всегда «длина» больше «ширины» (x > у).
В задачах, приводящихся к кубическому уравнению, встречалась третья
неизвестная — «глубина» (z), а произведение трех неизвестных именовалось
«объемом».
Область, в которой
вавилонянам принадлежит
основной успех—это решение
задач на квадратные
уравнения и системы,
сводящиеся к ним
ax^2 + bx + с = 0
Учение о квадратных уравнениях явилось основой нового этапа в развитии
математики, когда наряду с арифметикой и измерением фигур ее полноправной
частью стала алгебра.

15.

В геометрии рассматривались те же фигуры, что
и в Египте, плюс сегмент круга и усечённый
конус.
Вавилоняне умели вычислять площади
правильных многоугольников; им был знаком
принцип подобия.
Длину окружности вычисляли, утраивая диаметр;
с таким же значением π: = 3 определяли площадь
круга. Однако эта площадь S выражается не
непосредственно через диаметр, а через длину
окружности С по правилу S = С^2/12.
В клинописных текстах впервые появляется теорема
Пифагора.

16.

17.

Считается, что математика как наука
с теоремами и доказательствами,
зародилась именно в Древней
Греции. Великие математики
древности были греками.
Пифагора сказал - «Числа правят
миром». Спустя два тысячелетия
Галилей переформулировал
выражение «Природа разговаривает
с нами на языке математики». Греки
смогли подтвердить справедливость
этого высказывания.
Ионийская школа Древней Греции
считается родоначальницей
дедуктивной математики как науки.

18.

Появился ионийский способ записи
чисел, от 1 до 9 обозначали первые
девять букв греческого алфавита,
следующие девять – десятки, потом
сотни. Числа больше тысячи
обозначали те же буквы, но со
специальными знаками.
Первые математические доказательства
в Древней Греции принадлежат Фалесу
Милетскому VI век до н.э. Он доказал,
что величины вертикальных углов
равны, диаметр делит круг пополам,
треугольники равны по стороне и
прилежащим к ней углам.

19.

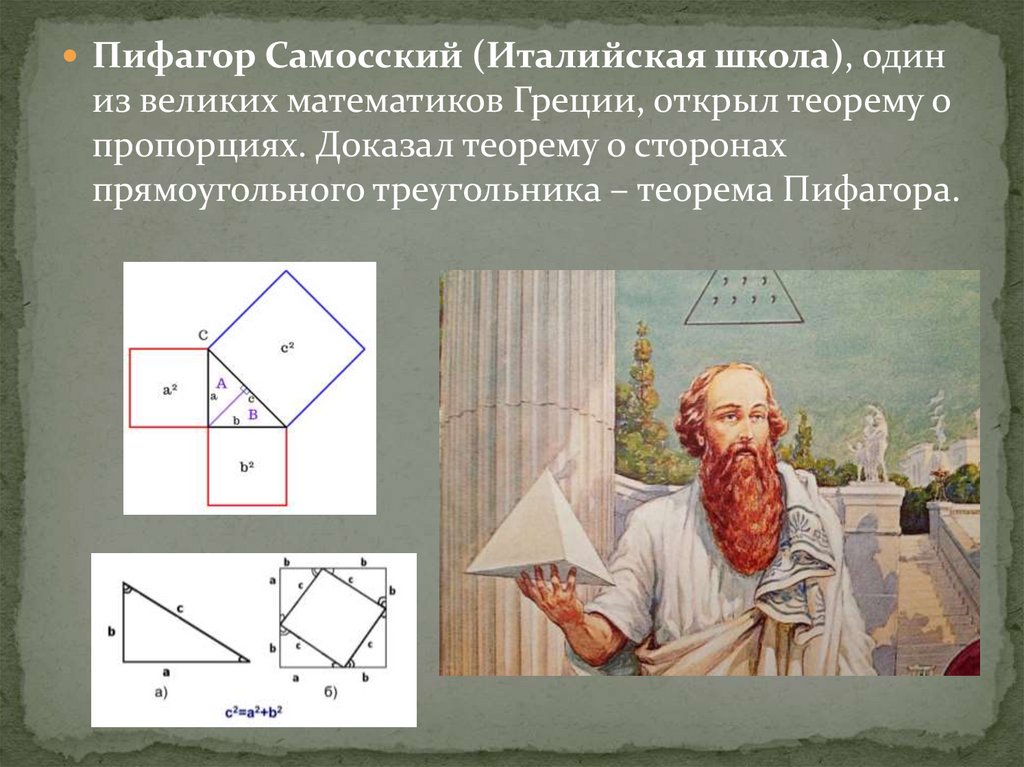
Пифагор Самосский (Италийская школа), один
из великих математиков Греции, открыл теорему о
пропорциях. Доказал теорему о сторонах
прямоугольного треугольника – теорема Пифагора.

20.

Значительных успехов
пифагорейцы добились в
стереометрии. Они открыли
построение четырех правильных
многоугольников - тетраэдра, куба,
октаэдра и додекаэдра:
а) тетраэдра, б) куба, в) октаэдра,
г) додекаэдра и д) икосаэдра.
Пифагорейцы рассматривали числа
как образующие элементы материи.
Числа отожествляли с
совокупностями точек, образующих
геометрические конфигурации.

21.

Платон (Афинская школа)
основанная в 389 г. Философская
школа Платона, известна под
именем Академии.
Евклид (Александрийская школа).
Ему принадлежат сочинения по
механике, оптике, музыке,
астрономии. Евклида обоснованно
считают «отцом геометрии».
Его главный труд «Начала». Первые
6 книг посвящены планиметрии, с 7 –
10 теории чисел, с 11 – 13
стереометрии.

22.

23.

24.

25.

Считается, Ариабхатта более
точно вычислил число «пи» –
3,1416, вычислил значение корней
2-й и 3-й степени.
Брахмагупта в стихотворной
форме написал
«Усовершенствованная наука
Брамы» сочинение в двадцати
книгах.
Первым ввел определение нуля и
отрицательные числа.
Положительные числа - как
имущество, отрицательные - как долг.

26.

27.

28.

Мусульманские ученые внесли свой вклад в
развитие математики и других наук.
Правители халифата организовали научные
центры, один из них— «Дом Мудрости» в Багдаде.

29.

Есть предположение - Омар Хайям открыл формулу возведения
двучлена a+b в степень n.
Трактат «О доказательствах задач алгебры и ал - мукабалы» термин «ал-джабр», это название алгебры, он толкует ее как
самостоятельную науку: науку о решении уравнений.
В решении кубических уравнений он использует геометрию –
конические сечения, параболу, равностороннюю гиперболу и
окружность. Он делит кубические уравнения на 14 типов.

30.

Улугбек – правитель Самарканда,
выдающийся ученый своего
времени астроном и математик,
внук великого полководца Тимура
(Тамерлана).
Мухаммед ибн-Муса ал-Хорезми
известный арабский математик.
Автором сочинения по арифметике
«Книга о сложении и вычитании по
исчислению индийцев».
Слово «алгоритм», образовалось по имени
автора, после перевода трактата на
латинский язык.
Трактат - «Китаб аль-джебр ва-льмукабала», от этого название произошёл
термин «алгебра».
В своих работах он определил характер
алгебры как практической науки без
аксиоматической основы, на несколько
веков вперед.

31.

Насир ад-Дин ат-Туси (XIII в.)
«Трактат о полном
четырехстороннике» посвящено
тригонометрии. Он рассматривает
тригонометрию как
самостоятельную науку, о решении
треугольников.
Его работа первое и полное
изложение тригонометрии.
Арабские математики составляли
таблицы значений
тригонометрических величин и
прежде всего синуса.
Ученые исламских стран наибольших
успехов добились в алгебре и
тригонометрии.

32.

33.

Ученые древнего Китая внесли большой вклад в мировую
науку.
Математики Китая открыли метод решения уравнений
первой степени с двумя и тремя неизвестными, научились
высчитывать дату затмения солнца.
Китайские иероглифические цифры по записи были
сложнее египетских цифр.

34.

Конфуций
считал математику одним из
«шести искусств», которым должен
владеть «благородный муж».
Конфуций высоко ценил
математические знания, не брал в
ученики тех, «кто не может по
одному углу (квадрата) судить о трех
остальных».
В XI в. до н. э. во время правления
династии Чжоу появились первые
учебники математики и точные
календари.
Была разработана система обучения
математики детей 6-8 лет.
До наших дней дошла «Математика в
девяти книгах», она представляет
собой сборник трудов разных
авторов, написанных с X по II века
до н.э. Труд собран финансовым
чиновником Чжан Цаном во II веке
до н. э. Каждая книга
предназначалась для разных
ведомств.

35.

Лю Хуэю, жившему в III веке н.э Написал самые значимые комментарии
в книги по математике. В самом значимом комментарии содержится
много доказательств.
Расчёт числа π методом вписанных правильных многоугольников.
Решение систем линейных уравнений методом, названным
впоследствии именем Гаусса.
Доказательство теоремы Пифагора.
Расчёт объёма призмы, пирамиды, тетраэдра, цилиндра, конуса и
усечённого конуса.

36.

Ли Е (1192-1279). Почти двадцать лет он прожил отшельником, за
это время он написал свою самую известную работу «Морское
зеркало измерений круга».
Работа посвящена решению уравнений, касающихся окружностей,
вписанных в треугольники.
Работы математиков древнего Китая практически не содержат
теоретических разработок. В основном их сочинения писались в
виде учебников и предназначались для обучения чиновников.

37.

38.

Математика в Западной Европе не имеет такого
древнего происхождения. Развитие научных
знаний приходятся на эпоху Средневековья и
особенно Возрождения.

39.

Анций Манлий Северин Боэций (V-VI век н.э.).Один из последних великих
ученых античности, основатель средневековой философии, автором
сочинения «Основы арифметики» «Квадривиальные учебники».
Перевел на латинский язык работы греческих ученых, написал комментарии к
сочинениям Аристотеля.

40.

Алкуин (ок. 730-804 гг.), известный под именем Флакк
Альбин - титул «первого просветителя средневековой
Европы».
Написанные им учебники использовали в школах до
конца Средневековья. Задачи из его учебника «Задачи
для оттачивания ума юношей» использовались в
течении нескольких столетий.
В наши дни известны некоторые его логические
головоломки, например: о волке, козе и капусте: «Один
человек должен был перевезти через реку волка, козу и
кочан капусты. Как перевезти всех на другой берег
целыми и невредимыми».

41.

Гербертом – первый профессиональный ученый католической Европы.
Открыл одно из первых учебных заведений в городе Реймс ( 940-1003 г.),
позднее папа римский Сильвестр II.
Его сочинения «Правила счета на абаке» и «Книжка о делении чисел». При
вычислениях на абаке вместо камешков, Герберт использовал нумерованные
жетоны – апексы.
Восстановил и усовершенствовал абак, забытый со времён Римской империи.
Герберт создал армиллярную небесную сферу, на ней обозначены небесный
экватор, тропики, эклиптика и полюса. Также разрабатывал
конструкцию астролябии, усовершенствованной позднее.
В 1003 году Герберт был лишен папского сана, в обвинении было сказано: «он
слишком хорошо умеет делить большие числа, не иначе, как ему помогает
дьявол».

42.

Герард Кремонский - итальянец,
математик, астролог, философ и
врач, известный переводчик того
времени.
Перевел на латынь: «Начала»
Евклида, «Измерение круга»
Архимеда, «Конические сечения»
Аполлония, «Альмагест» Птолемея,
алгебру ал-Хорезми и другия
трактаты по физике, философии,
логике.
Леонардо Пизанский или
Фибоначчи – итальянец, первый
известный математик XII века. Он
открыл для европейцев алгебру и
внедрил индийские цифры.
Его "Книга абака" - возвышается над
европейской литературой по
математике 12-14 вв.. В ней изложены
разнообразные математические
методы, много задач с
доказательствами.

43.

«Золотое сечение» - Фибоначчи, это
деление отрезка на две части таким
образом, чтобы отношение большей
к меньшей части было равно
отношению всего отрезка к большей
части. Обозначается буквой «фи»
или φ.
Лука Пачоли итальянец ставший
монахом XV век. В трактате «Сумма
арифметики» изложены правила
приема действий над целыми и
дробными числами, задачи на
проценты, пропорции, решение
линейных, квадратных и
биквадратных уравнений. Его книги
«Алгебра» и «Пять правил
Платона».
Леонардо да Винчи, большой друг
Луки Пачоли, создал для его книги
иллюстрации многогранников, грани
которых являются правильными
многоугольниками.

44.

Региомонтан (Иоганн Мюллер) - выдающийся
немецкий астроном и математик. Написал работу
«О всех видах треугольников». В ней он
рассмотрел тригонометрию как самостоятельный
предмет, привел теорему синусов как на
плоскости, так и в сферической геометрии.
Календарь

45.

Проективная геометрия берет свое начало в эпоху
Возрождения. Художники решили, что для
реалистичности картины она должна следовать
законам проекции. По этой теории, все прямые
лучи света исходящие из глаз смотрящего к
различным точкам представляемого изображения,
образуют проекцию.

46.

Джероламо Кардано (1501 —
1576) итальянский математик.
Трактат по алгебре «Великое
искусство», содержал формулы
решения кубического уравнения.
Лодовико Феррари (1522-1565)
итальянский математик, нашел
общее решение уравнения
четвёртой степени. Был учеником
миланского математика Джероламо
Кардано.

47.

Джон Непер (1550–1617)
шотландский математик, изобрел
логарифмы, первый опубликовал
логарифмические таблицы.
Симон Стевин фламандский
математик издал книгу «Десятая», в
ней изложены правила действия с
десятичными дробями.
Титульный лист фламандского
издания «Десятая».

48.

Франсуа Виет (1540–1603)
французский математик
основоположник символической
алгебры. Для обозначения
неизвестных и постоянных величин
стал применять буквы.
Рене Декарт (1596 -1650)
французский математик создал
новую систему координат.

49.

Пьер Ферма – Французский математик. Один из
создателей аналитической геометрии,
математического анализа, теории вероятностей и
теории чисел.

50.

Формула Ньютона - Лейбница — одна из основных формул
математического анализа, одного из его разделов — анализа
бесконечно малых чисел.
В современной формулировке она излагается следующим образом:
Если функция f непрерывна на отрезке [a, b] и если F есть
функция, производная которой равна f на интервале (a, b), то:
Кроме того, для любого x из интервала (a, b):

51.

Давид Гильберт и Карл Вейерштрасс
создадут функциональный анализ.
Георг Кантор – теорию множеств,
Джордж Буль – математическую
логику, Карл Пирсон –
математическую статистику.

52.

53.

У славян, как и у других народов,
математика развивалась на фоне бытовых
нужд. Для счета пользовались палочками
с зарубками, узелками.

54.

Князь Владимир Святославичем (958 1015). Первая школа открытая при
князе Владимире для «нарочитой
чади» - детей (мальчиков) знатных
людей.
Ярослав Мудрый (978-1054) В 1028 г.
была открыта школа в Новгороде.

55.

Роман Ростиславович князь
смоленский. Открыл школы в
Смоленске.
Ярослав Осмомысл Галицкий
предписывал открывать школы и
обучать детей в монастырях.

56.

Монах Кирик Новгородский (1110 – 1158?) - «числолюбец».
«Учения о числах» (1136 г)
В своем сочинении он подсчитал, сколько месяцев, дней,
часов он прожил. Вычислил в месяцах, неделях, днях время
от «сотворения мира» до 1134 года. Вычислил на будущее дни
церковных праздников.

57.

Числа в древней Руси, для отличия
букв от цифр, над буквой ставилась
волнистая линия – титло.
Запись больших чисел: 10 000 – тьма,
буква обведенная в определенный
круг, 100 000 – легион, букву
обрамлял другой круг.

58.

Первые статьи с математическими
расчетами впервые были
опубликованы в юридическом
сборнике «Русская правда» в XI
веке.
После освобождения Руси от татаромонгольского ига во время
правления Ивана Грозного было
введено бесплатное начальное
образование (школы при церквях).

59.

Первая рукопись на русском языке
по теоретической геометрии —
Синодальная № 42, 1625 год,
хранится в Государственном
историческом музее.
Илья Копиевский. В 1699 году, в
Голландии была издана книга по
математике «Руковедение в
арифметику».

60.

Первое печатное издание «Руковедения в арифметику» в России
(1682)
«Считание удобное, которым всякий человек купующий или
продающий зело удобно изыскати может число всякие вещи.
А како число вещей и вещам число цены изыскати, и о том
читая в предисловии к читателю совершенно познаешься». В
книги содержались таблицы умножения до 100 и другие
арифметические факты.

61.

Леонтий Филиппович
Магницкий (1669-1739) первым
учителем математики и морских
наук в России.
Первый учебник "Арифметика"
Магницкого 1703 год .
Состоял из пяти частей;
1.О числах целых.
2.О числах ломаных или с долями.
3.О правилах подобных, в трех, в
пяти и в семи перечнях.
4.О правилах фальшивых, еже есть
гадательных.
5. О правилах радиксов, квадратных
и кубических, геометрии
принадлежащих.
Задачи из арифметики
Магницкого

62.

Леонард Эйлер
В 1724 г открыта
Петербургская Академия
наук с университетом и
гимназией.
«Руководство к
арифметике для
употребления в гимназии
императорской Академии
наук» Эйлера, учебник
математики в двух частях.

63.

Семион Кириллович
Котельников (1723-1806). Второй
русский академик Петербургской
Академии наук .
Михаил Софронов (1729-1760) талантливый русский математик.

64.

Великий русский
математик и механик
Пафнутий Львович
Чебышев (1821-1894
годы). За работу
«Вычисление корней
уравнений» в 1841 году
награжден серебряной
медалью.
За докторскую
диссертацию «Теория
сравнений» удостоен
специальной премии
Петербургской
академии наук.

65.

Михаил Васильевич
Остроградский (1801 —1861г.)
признанный лидер
математиков Российской
империи (1830—1860 годы).
В разные годы вышло много
его работ и статей по
математики.
В 2001 году ЮНЕСКО
включила Михаила
Остроградского в перечень
выдающихся математиков
мира
Работа по теории чисел:
«Таблицы первообразных
корней всех простых чисел,
меньших 200».

66.

Виктор Яковлевич
Буняковский (1804 – 1889 г.) математик, вице-президент
академии наук в 1864–1889
годах, педагог, историк
математики. Внёс
значительный вклад в теорию
чисел.
Самосчеты Буняковского
Планиметр
Пантограф

67.

Николай Иванович
Лобачевский (1792 1856) – русский
математик,
первооткрыватель
неевклидовой
геометрии.
из рукописи
Лобачевского

68.

фигуры Лобачевского
пятый постулат Лобачевского
Лобачевский сформулировал 5 постулатов, которые послужили
созданию новой неевклидовой геометрии:
а) Через две точки можно провести одну и только одну прямую
б) Прямая продолжается бесконечно
в) Из любого центра можно провести окружность любым радиусом
г) Все прямые углы равны между собой
д) На плоскости через точку, не лежащую на данной прямой, проходит
более чем одна прямая, не пересекающая данную

69.

Геометрия Римана;
Евклидова геометрия;
геометрия Лобачевского
К сожалению, всемирная слава и признание пришли к
великому ученому после смерти в 1870-е годы. Н.И
Лобачевский был признан одним из первых русских
математиков XIX века.

70.

Софья Васильевна Ковалевская
(1850 – 1891 г) – русский математик,
член-корреспондент
Петербургской Академии наук.
Первая женщина – профессор
математики в России и в Северной
Европе.
Ковалевская открыла третий
классический случай
разрешимости задачи о вращении
твердого тела вокруг неподвижной
точки. За что получила премию
Парижской академии за
исследование о вращении
тяжёлого несимметричного
волчка.

71.

Теорема Коши — Ковалевской гласит, что если в
дифференциальном уравнении коэффициенты
определены и являются аналитическими
функциями, а искомое решение f(x) имеет
известное значение в какой-то точке X, то в
области рядом с точкой X решение f(x) существует
и единственно.

72.

Выдающиеся русские математики нестандартно
мыслили, упорно трудились, совершали
удивительные открытия. Их имена стали известны
не только в России, но и во всем мире.
Андрей Николаевич Колмогоров (1903-1987) –
признанный в мире глава теории вероятностей.