Решение простейших комбинаторных задач методом перебора

1.

Разработано:
Учитель математики
МБОУ СОШ №8
Исакова Марина Викторовна
г. Бердск

2.

Вам требуется найти количество всех способов,
которыми можно составить трехцветный флаг
из горизонтальных полос красного, белого и синего цветов.
Для того чтобы найти все эти способы, проведем небольшой
эксперимент:
вы будете переставлять полоски, которые расположены у вас
на парте, а результат этих
перестановок фиксировать в тетрадь.
Давайте обозначим каждый цвет буквой, с которой
он начинается К – красный, Б – белый, С – синий.

3.

1 способ – перебор вариантов.
БСК
БКС
КСБ
КБС
СКБ
СБК
В этой таблице 2 столбца, 3 строки,
значит всего 2*3=6 способов
2 способ – «Дерево возможностей»

4.

5.

В 6А классе во вторник 5 уроков: физкультура, русский язык, литература,
обществознание и математика. Сколько можно составить вариантов
расписания на день, зная точно что математика - последний урок?
Решение: Закодируем О - обществознание, Р – русский язык, Л - литература,
М – математика, Ф- физкультура.
ЛОРФ
ОЛРФ
РЛОФ
ФЛОР
ЛОРФ
ОЛФР
РЛФО
ФЛРО
ЛРОФ
ОРЛФ
РОЛФ
ФОЛР
ЛРФО
ОРФЛ
РОФЛ
ФОРЛ
ЛФОР
ОФЛР
РФЛО
ФОРЛ
ЛФРО
ОФРЛ
РФОЛ
ФРОЛ
Ответ: 24 варианта

6.

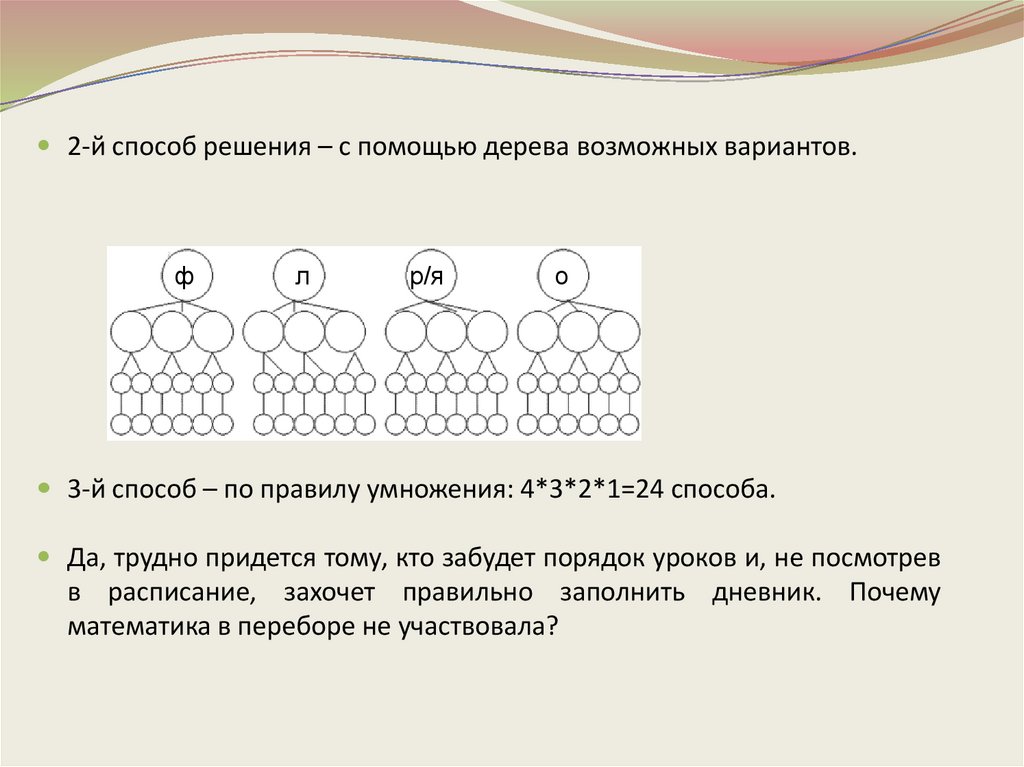
2-й способ решения – с помощью дерева возможных вариантов.
ф
л
р/я
о
3-й способ – по правилу умножения: 4*3*2*1=24 способа.
Да, трудно придется тому, кто забудет порядок уроков и, не посмотрев
в расписание, захочет правильно заполнить дневник. Почему
математика в переборе не участвовала?

7.

Проказница мартышка, осел, козел,
Да косолапый мишка
Затеяли сыграть квартет…
Вам знакомо это произведение?
Сколькими способами можно рассадить этих четырех музыкантов в
один ряд?
Давайте решим эту задачу с помощью «Дерева возможностей».
Если на первое место мы посадим мартышку, то будет …
Сколько способов? 3*2*1=6 способов.
Но на первое место мы можем посадить и осла, и козла, и мишку, т. е.
4*3*2*1=24.
Итак, если бы в спор не вмешался соловей, то этим горе-музыкантам пришлось
бы пересаживаться 24 раза.

8.

Сколькими способами можно из цифр 0, 2, 3, 5
составить четырехзначное число такое, чтобы цифры в
нем не повторялись?
Ответ: 3*3*2*1=18 способов.
Вывод: Оказывается, не все задачи можно решить по правилу умножения,
поэтому при решении задач на перестановки
нужно быть очень внимательными.