Волшебное зеркало Эшера

1.

«Волшебное зеркало
Эшера».
ОРНАМЕНТАЛЬНОЕ И ГЕОМЕТРИЧЕСКОЕ ИСКУССТВО МАРИУЦА ЭШЕРА

2.

«В огромном саду геометрии
каждый найдет букет себе
по вкусу.»
Давид Гильберт

3.

Многие художники создавали картины, в основе которых лежала геометрия. Среди них са
мым известным является гениальный голландский художник-график Мауриц Эше - отец
математического искусства.
Эшер был известен, прежде всего, своими литографиями, гравюрами на дереве и металле,
в которых он мастерски исследовал пластические аспекты понятий бесконечности и
симметрии, а также особенности психологического восприятия сложных трёхмерных
объектов.

4.

Гипотеза: если я познакомлюсь с орнаментальным и геометрическим искусством
М. Эшера, а затем изучу принципы построения мозаик художника, то я смогу сделать паркет,
похожий на его работы.
Исходя из этого, я обозначила для себя цели и задачи проектной работы.
Цель: изучить работы Эшера и научиться составлять паркеты, похожие на работы
художника.
Задачи работы:
• Познакомиться с биографией Мариуца Эшера.
• Изучить работы М.Эшера, связанные с паркетами и мозаиками.
• Понять принцип схемы работ Эшера.
• Составить схему и придумать свой паркет.

5.

Исследование работ Эшера.
В 1916 году Эшер выполнил свою первую графическую работу.
Это гравюра на фиолетовом линолеуме - портрет своего отца.
В то время Эшер посещал мастерскую художника Герта Стигемана,
имевшего печатный станок для того, чтобы изготавливать гравюры.
На этом самом станке были отпечатаны первые гравюры Эшера (рис.1)
В конце тридцатых годов Эшер продолжал эксперименты с мозаиками и трансформациями. В то
время он создал мозаику в виде двух птиц, летящих навстречу друг другу, которая легла в основ
у картины "День и ночь" (рис.2).Эшером был составлен паркет «Небо и вода», в
котором из белых рыб получаются птицы (рис.3).

6.

7.

Мозаика и паркеты в работах Эшера
Мозаичные изображения известны с античных времён. Первоначально эт
о были несложные узоры из камешков, затем художники стали создавать
целые мозаичные картины.
Регулярное разбиение плоскости, называемое мозаикой или паркетом –
это набор замкнутых фигур, которыми можно замостить плоскость
без пересечений фигур и просветов между ними.
Эшер интересовался всеми видами мозаик, а также ввёл собственный
вид, который назвал "метаморфозами", где фигуры изменяются
и взаимодействуют друг с другом, а иногда изменяют и саму
плоскость. Интересоваться мозаиками Эшер начал в 1936 году
во время путешествия по Испании.

8.

Математики доказали, что для регулярного разбиения плоскости подходят только три правильных многоугольник
а:
треугольник, квадрат и шестиугольник.Убедимся в том, что никакой другой правильный многоугольник, кроме перечис
ленных выше, паркета не образует. Как известно из геометрии, сумма внутренних углов выпуклого n-угольника равна
:(n – 2) · 180º где n – число вершин (углов) многоугольника Тогда величина каждого угла правильного многоугольник
а равна
кол-во углов n
3
4
5
6
7
8
9
10
11
12
величина угла
60
90
108
120
128,57
135
140
144
147,27
150
А теперь составим таблицу, где α– величина угла правильного многоугольника, а k– число углов, сходящихся в
одной точке (вершине) паркета.
Сумма углов правильных n-угольников, сходящихся в одной точке (вершине) паркета, равна 360º, значит k=360:α
α
60
90
108
120
128.57 135
140
144
147.27 150
k
6
4
3.3
3
2.8
2.7
2.6
2.5
2.4
2.4
То есть у правильного треугольника α= 60º, то k = 360: 60º, т.е. k= 6, значит, в одной вершине паркета могут
сходиться 6 правильных треугольников.
А у правильного пятиугольника α = 108º, значит k= 3,3, следовательно, не существует паркета из правильных
пятиугольников, и так далее.

9.

Паркеты в работах Эшера
Эшер использовал базовые образцы паркетов, применяя к ним трансформации, которые в геометрии
называются симметрией, отражением, смещением и др. Также он исказил базовые фигуры, превратив их в
животных, птиц, ящериц и проч. Эти искажённые образцы мозаик имели в своей основе правильные
треугольники, квадраты или шестиугольники.
Эволюция 1

10.

Мозаику рептилий Эшер использовал во многих своих работах. В "Эволюции 1" можно проследить развитие искажени
я
квадратной мозаики в центральную фигуру из четырех ящериц.
Центральная идея самовоспроизведения, взятая на вооружение Эшером, обращается к загадке человеческого сознания
и способности человеческого мозга обрабатывать информацию так, как не сможет обработать ни один компьютер.
Самовоспроизведение является направленным действием. Руки рисуют друг друга, создавая самих себя. При этом сами
руки и процесс их самовоспроизведения неразделимы. Конечно, мы не состоим из уменьшенных копий самих себя, но
каждая клетка нашего тела несет в себе информацию обо всём теле в виде ДНК. Использование Эшером различных
математических фигур и законов не ограничивается лишь вышеприведёнными примерами.

11.

«Человек веками пытался объяснить
и создать порядок, красоту и
совершенство с помощью
симметрии.»
Герман Вейль

12.

Составляем свой паркет.
Кажется, что придумать паркет, похожий на работу Эшера, очень сложно. Но некоторые геометрические з
нания и умения помогут нам понять принцип построения паркетов Эшера. На паркете Мориса Эшера нас
будут интересовать лишь линии, их изгибы и повторы и то как геометрическая фигура трансформируется в
объекты живой и неживой природы. Посмотрите, как квадраты преобразуются в собак (Рис. 20).
Значит для создания паркета нам нужно следовать пунктам:
Возьмите за основу любую геометрическую фигуру. Например,
возьмём квадрат (рис.21).

13.

Изменим одну сторону квадрата. Тогда, чтобы ячейки
«вдвинулись» одна в другую, так же надо изменить и
противоположную сторону (рис. 23).У нас получилась
ячейка. Продолжим рисовать такие же ячейки, и мы
Рис.22
Рис. 23
Рис. 24
получим паркет.
Мой «Листопад».
За основу я взяла квадрат. Составила паркет из квадратов и в каждом нарисовала по два
треугольника, постоянно меняя их расположение:
в левом ряду: сначала в нижнем левом углу, потом в нижнем правом, затем снова в
нижнем левом;
в следующем ряду сначала в верхнем левом углу, потом в верхнем правом, затем снова
в верхнем левом и т.д. Получилось изображение, напоминающее стрелки (рис. 28).

14.

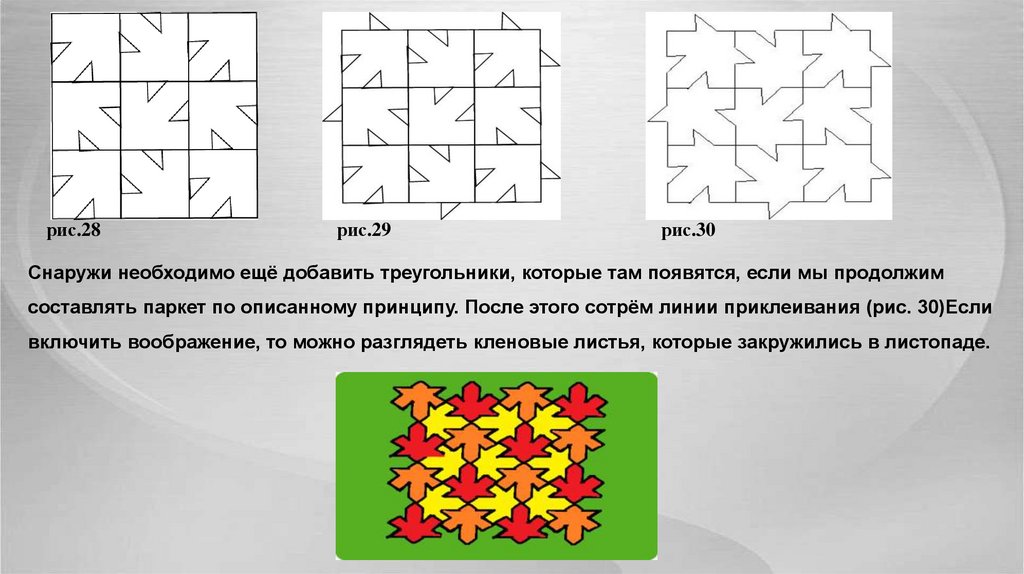
рис.28
рис.29
рис.30
Снаружи необходимо ещё добавить треугольники, которые там появятся, если мы продолжим
составлять паркет по описанному принципу. После этого сотрём линии приклеивания (рис. 30)Если
включить воображение, то можно разглядеть кленовые листья, которые закружились в листопаде.

15.

Паркет «Клоуны»
Для начала я решила изобразить простой паркет «Клоуны». Мы берём за основу прямоугольник (рис. 25 (1)).
Вырежем снизу квадрат и установим его на противоположную сторону прямоугольника сверху (в дальнейшем, это буде
т
основой для головы клоуна) и точно так же изменим нижнюю сторону квадрата (рис. 25 (2))
Снизу на сторонах квадрата строим три треугольника, вырезаем их, передвигаем и приклеиваем к сторон
верхнего квадрата (рис. 25 (3, 4)). Это будут колпак и волосы клоуна.
Вырежем четырёхугольник на правой стороне прямоугольника, передвинем и приклеим его к левой стороне
(это будут руки клоуна)(рис. 25 (5, 6))
Срежем у прямоугольника два верхних угла в виде прямоугольных треугольников и сдвинем их вниз. (рис. 25 (7)).
Так мы оформим плечи и ботинки клоуна (рис. 25 (8))
Прорисовываем детали (рис. 26).
Собираем паркет (рис. 2
7).

16.

Вывод
Я познакомилась с орнаментальным и геометрическим искусством М. Эшера, изучила принципы
построения мозаик художника, узнала много нового о паркетах. В результате я составила схемы своих
геометрических паркетов, а также поняла, что, если за основу взять обычную геометрическую фигуру и
выполнить
некоторые преобразования, можно получить художественную мозаику, красочные паркеты:
«Клоуны» и «Листопад» и, переведя их на кружку, футболку и кепку, сделала отличные подарки для друзей
ЗАКЛЮЧЕНИЕ
Практическую значимость моей работы вижу в том, что:
Знания, которые я получила, во время работы над проектом, могут использовать школьники,
чтобы рисовать свои необычные паркеты. Эти паркеты можно превратить в замечательные подарки.
Я узнала много нового о художнике Морисе Эшере, о секретах геометрии и уверена, что эти знания
пригодятся мне в будущем.
Моя работа может быть использована учителями на уроках или факультативных занятиях по геометрии.

17.

«Высшее назначение математики –
находить порядок в хаосе, который
нас окружает».
Норберт Винер, основатель
кибернетики

18.

КОНЦА ПОЗНАНЬЮ НЕТ!