Похожие презентации:
Дискретные АС
1.
Автоматика и управлениеТема 9. Дискретные АС
ПЗ 13 Определение временных характеристик и
устойчивости дискретных АС.
2.
Задача №1.Определить Z-изображение функции
x(t)=1+2t2-e-2t,
если Т=0,2с.
Решение:
X(z)=Z[{xi}]=Z[x(iT)];
i=0, …
Находим решетчатую функцию {xi}:
i=0 x0=1+2(0 0,2)2- e-2(0 0,2)=0;
i=1 x1=1+2(1 0,2)2- e-2(1 0,2)=1,08- e-0,4;
i=2 x2=1+2(2 0,2)2- e-2(2 0,2)=1,32- e-0,8;
{xi}={0; 1,08- e-0,4; 1,32- e-0,8; …}
1
1
2
x
z
x
x
z
x
z
...
X(z)= i
0
1
2
i 0
X(z)= 0+ (1,08- e-0,4)z-1+(1,32- e-0,8 )z-2+….
{xi}={x0, x1, x2, …},
3.
Задача №2.Задан оператор ЦВМ:
2yi+5yi-1-7yi-3=0,5xi-2+3xi-5.
Определить W(Z) ЦВМ.
Решение:
W ( z)
Y (z)
X ( z)
Применим Z-преобразование к разностному уравнению,
описывающему работу ЦВМ:
2Y(z)+5z-1Y(z)-7z-3Y(z)=0,5 z-2X(z)+3 z-5X(z);
Y(z)[2+5z-1-7z-3]=X(z)[ 0,5z-2+3z-5].
Y ( z)
0,5 z 2 3z 5
W ( z)
X ( z ) 2 5 z 1 7 z 3
4.
nCn
Ci
C1
C2
F ( p) C 0
C0
,
p p1 p p2
p pn
i 1 p pi
Задача №3
Задана передаточная функция непрерывного элемента
W( p )
5( p 1 )
( 0 ,5 p 1 )( 2 p 1 )
на которой воздействует дискретный сигнал с периодом дискретности
Т=0,2с.
Требуется определить Z-передаточную функцию W(z) этого элемента.
Решение:
1.Разложим передаточную функцию W(p) на элементарные дроби:
W ( p)
C2
C1
5( p 1)
5( p 1)
p p1 p p 2
(0,5 p 1)(2 p 1) ( p 2)( p 0,5)
где р1=-2; р2=-0,5 корни А(р)=0.
Определим коэффициенты С1 и С2:
5.
5( p 1)( p 2)( p 0,5)
C2
C1
а)
p 0,5
p 2
С1(р+0,5)+ С2(р+2)= 5(р+1)
р0 0,5C1 + 2C2 = 5,
p-1 C1 + C2 = 5 C1=3,33; C2=1,667.
б)
В( р )
5( p 1)
С1
А ( р ) р р1
2 p 2,5 р 2
С2
=3,33
Ci
B( p )
A
(1)
,i 1, n
( p ) p pi
В( р )
5( p 1)
=1,667
А ( р ) р р 2
2 p 2,5 р 0,5
Определим W(z)
W(z)=
Z
р [W(p)]=
Z 3,33 e
2 ( iT )
1 3,33
1,667
Z 3,33
Z L
Z
р р 2 р 0 ,5
p 2
1 1,667
L
p
0
,
5
Z 1,667 e 0 , 5 ( iT )
=3,33(1+e-2 0,2z-1+e-2 0,2 2z-2+…)+
+1,667(1+e-0,5 0,2z-1+e-0,5 0,2 2z-2+…)=
6.
=3,33(1+e-2 0,2z-1+e-2 0,2 2z-2+…)+ 1,667(1+e-0,5 0,2z-1+e-0,5 0,2 2z-2+…)=1
3,33
1,667
5 4 ,12z
1 e 2 0, 2 z 1 1 e 0,5 0, 2 z 1 ( 1 0 ,67 z 1 )( 1 0 ,9 z 1 )
Данный результат можно получить, используя таблицы
Zр преобразований и учитывая, что Т=0,2с.
3,33
1,667
р 2 р 0 ,5
Z
W(z)= р
x(t)
e
at
X(p)=L[x(t)]
1
p a
X ( z ) Z [ x( t )] zp [ X ( p )]
1
1 e aT z 1
qn 1
q 1
1
1 q 1 q 2
1 q 1
1 q q 2 q3
7.
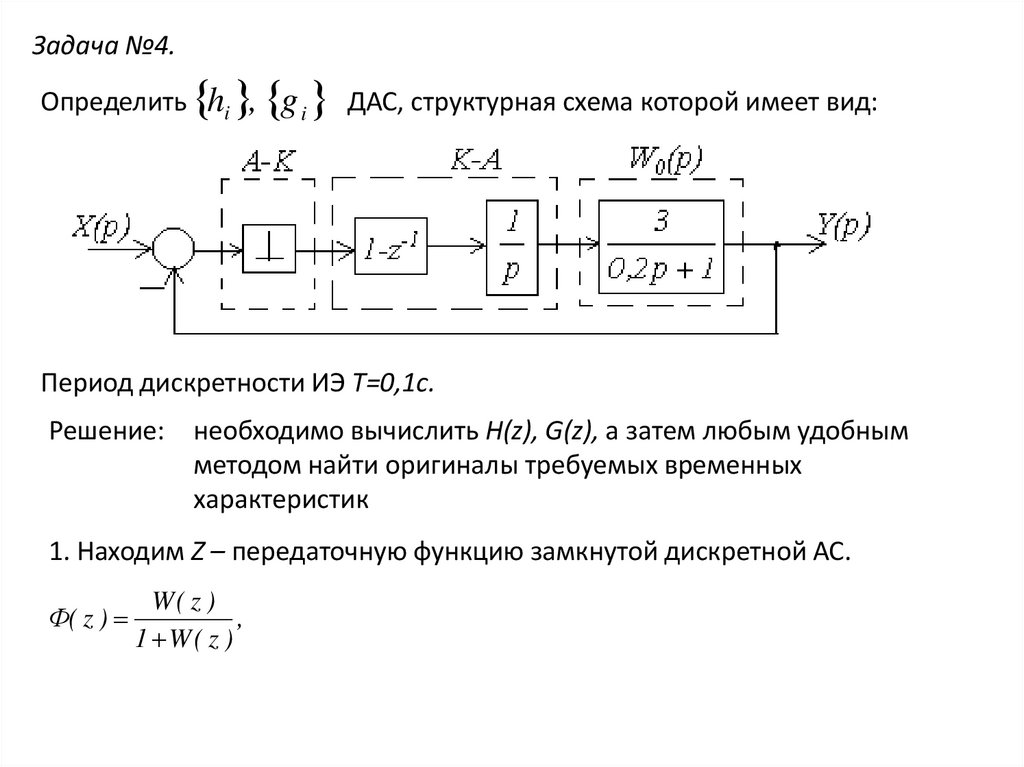
Задача №4.Определить hi ,
g i ДАС, структурная схема которой имеет вид:
Период дискретности ИЭ T=0,1c.
Решение: необходимо вычислить H(z), G(z), а затем любым удобным
методом найти оригиналы требуемых временных
характеристик
1. Находим Z – передаточную функцию замкнутой дискретной АС.
Ф( z )
W( z )
,
1 W( z )
8.
13
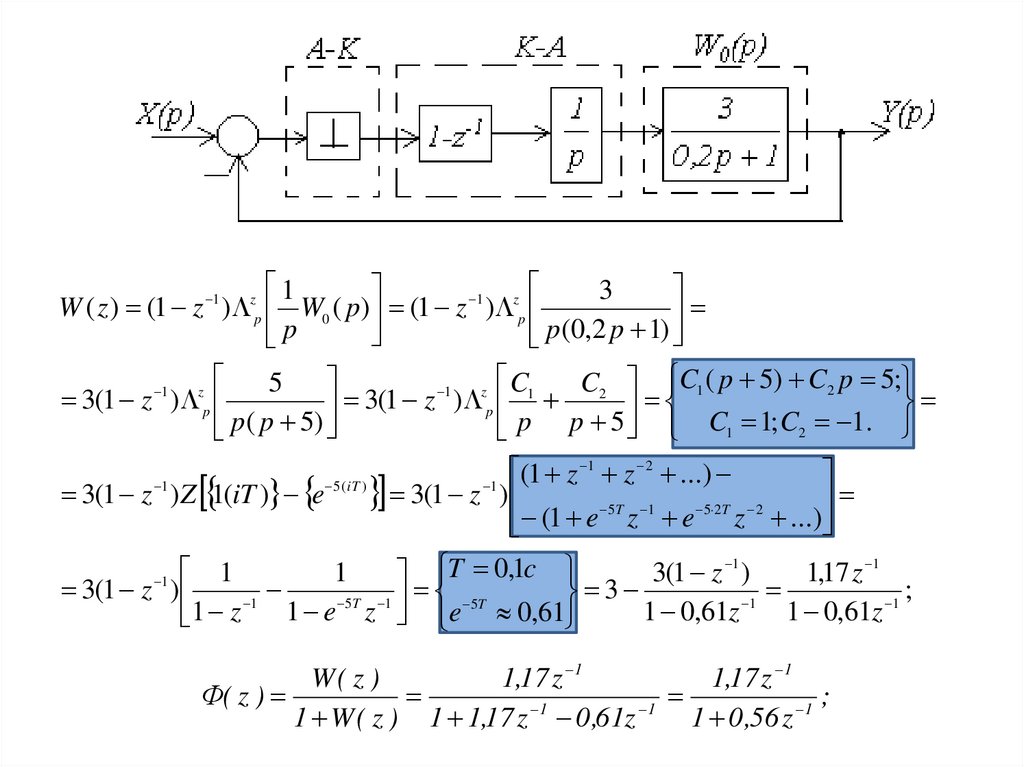
W ( z ) (1 z 1 ) zp W0 ( p ) (1 z 1 ) zp
p
p (0,2 p 1)
C1
5
C2 C1 ( p 5) C2 p 5;
1
z
3(1 z 1 ) zp
3
(
1
z
)
p
p ( p 5)
p p 5 C1 1; C2 1.
1
2
(
1
z
z
...)
1
5 ( iT )
1
3(1 z )
3(1 z ) Z 1(iT ) e
5T 1
5 2T 2
(1 e z e z ...)
1
1
3(1 z 1 )
1,17 z 1
T 0,1c
1
3(1 z )
5T
;
3
1
5T 1
1
1
1
z
1
e
z
1
0
,
61
z
1
0
,
61
z
e 0,61
W( z )
1,17 z 1
1,17 z 1
Ф( z )
;
1
1
1
1 W ( z ) 1 1,17 z 0 ,61z
1 0 ,56 z
9.
W( z )1,17 z 1
1,17 z 1
Ф( z )
;
1
1
1
1 W ( z ) 1 1,17 z 0 ,61z
1 0 ,56 z
Определим весовые коэффициенты, решая разностное уравнение,
представляющее оператор ДАС:
Yi+0,56yi-1=1,17xi-1;
x( iT ) 1,0 ,0 ,0 ,...
i=0
g0+0,56g-1=1,17x-1
g0= 0
i=1
g1+0,56g0=1,17x0
g1=1,17
i=2
g2+0,56g1=1,17x1
g2=-0,56 1,17=-0,66
i=3 ….
Определим весовую функцию ДАС, методом разложения её изображения в
ряд Лорана:
1,17 z 1
1
2
G( z ) Ф( z )
g
g
z
g
z
...
0
1
2
1
1 0 ,56 z
1,17z-1=(g0+g1z-1+g2z-2+…)(1+0,56z-1)
10.
1,17z-1=(g0+g1z-1+g2z-2+…)(1+0,56z-1)z0 0=g0,
z-1 1,17=0,56g0+g1
g1=1,17,
z-2 0=0,56g1+g2
g2=-1,17 0,56=-0,6552,
z-3 0=0,56g2+g3
g3=0,6552 0,56 0,37,
g i 0;1,17 ; 0 ,66 ;0 ,37 ;...
Определим переходные коэффициенты ДАС, используя теорему
разложения:
1
1
2
Z
1
(
t
)
Z
1
(
iT
)
Z
1
,
1
,
1
,
...
1
z
z
...
;
1 z 1
1,17 z 1
Z (t) Z ( iT ) Z 1,0,0, ... 1 .
Ф( z )
;
1
1 0,56 z
Ф( z )
1,17 z 1
z2
H ( z ) Ф( z ) X ( z )
1 1
1
1
1
1 z
( 1 0 ,56 z )( 1 z )
z z
1,17 z
.
( z 0 ,56 )( z 1 )
n
Так как m<n, то h0=0. hi= C k z k
k 1
i 1
где k=1, n
i=1,2,…
11.
1,17 zH ( z)
.
( z 0,56)( z 1)
n
hi= C k z k
i 1
k 1
Ci
B( p )
A
(1)
( p ) p pi
z1=-0,56; z2=1; A(1)(z)=2z-0,44;
h1 C1 z11 1 C 2 z 21 1 C1 C 2 1,17;
2 1
1 1
h2 C z
C2 z
2 1
2
0 ,65
1,17
( 0 ,56 )
0 ,515;
1,56
1,56
h3 C1 z13 1 C 2 z 23 1 ...
hi 0;1,17;0 ,515;0 ,882;0 ,676;0 ,791;0 ,727;...
Переходные коэффициенты можно получить, воспользовавшись
уравнением связи между g i и hi
i
hi g k .
k 0
,i 1, n
12.
Задача № 5Дискретная АС описывается передаточной функцией
0 ,1z 2 z 0 ,8
Ф( z ) 3
2 z z 2 3z 1
Оценить устойчивость данной АС по сходимости ряда весовых
коэффициентов.
13.
0 ,1z 2 z 0 ,8Ф( z ) 3
2 z z 2 3z 1
Решение
Определим весовые коэффициенты {qi}
Ф(z)= G(z)= g0+ g1z-1+g2z-2+...
Приведем выражение Ф(z) к отрицательным степеням
0,1z 2 z 0,8 z 3 0,1z 1 z 2 0,8 z 3
3
3
2
2 z z 3z 1 z
2 z 1 3 z 2 z 3
Приравняем данное выражение к степенному ряду весовых
коэффициентов относительно z-i,
0,1z-1+z-2+0.8z-3=(2+z-1-3z-2+z-3)(q0+q1z-1+q2z-2+ ),
z0
z-1
z-2
z-3
z-4
z-5
0=2g0 g0=0;
0,1=g0+2g1 g1=0,05;
1=-3g0+g1+2g2 g2=0,475;
0,8=g0-3g1+g2 +2g3 g3=0,2375;
0=2g4+g3-3g2 +g1 g4=0,7125;
0=2g5+g4-3g3 +g2 g5=-0,2375;
Оценим сходимость ряда
весовых коэффициентов
g
i
0
Дискретная АС с данной
передаточной функцией
неустойчива.
14.
Задача №6.С помощью необходимого и достаточного условия устойчивости оценить
устойчивость АС, передаточная функция которой имеет вид:
Ф(z)=
1.1z 0,8
z 2 0,2 z 1.2
Решение:
Вычислим корни характеристического уравнения
А(z)= z2+0,2z+1.2=0
Z 1,2
0 ,2 0 ,04 4 ,8 0 ,2 4 ,76
2
2
z1=-0.1+j1,09;
z2=-0,1-j1,09
Оценим соответствие корней характеристического уравнения
необходимому и достаточному условию устойчивости
zi 1
z1 0,1 j1,09 1,198 1
z 2 0,1 j1,09 1,198 >1
Вывод: система не устойчива
15.
Задан алгоритм ЦВМ. Найти z-передаточную функцию ЦВМ Wцвм(z)1.
11.
2.
12.
3.
13.
4.
14.
5.
15.
6.
16.
7.
17.
8.
18.
9.
19.
10.
20.
16.
Задана z-передаточная функция Ф (z) дискретной системы. Записать разностноеуравнение системы
1.
11.
2.
12.
3.
13.
4.
14.
5.
15.
6.
16.
7.
17.
8.
18.
9.
19.
10.
20.
17.
Задана z-передаточная функция Ф (z) замкнутой дискретной системы. Исследоватьустойчивость системы
1.
2.
3.
4.
5.
6.
7.
8.
9.
10.
11.
12.
13.
14.
15.
16.
17.
18.
19.
20.
18.
Задано изображение X(p) входного сигнала x(t) дискретной cистемы с периодомдискретности T. Определить Z-изображение X(z) сигнала x(t).
1.
2.
3.
4.
5.
6.
7.
8.
9.
10.
11.
12.
13.
14.
15.
16.
17.
18.
19.
20.
19.
Таблица преобразований Лапласа: Z иzp -преобразований




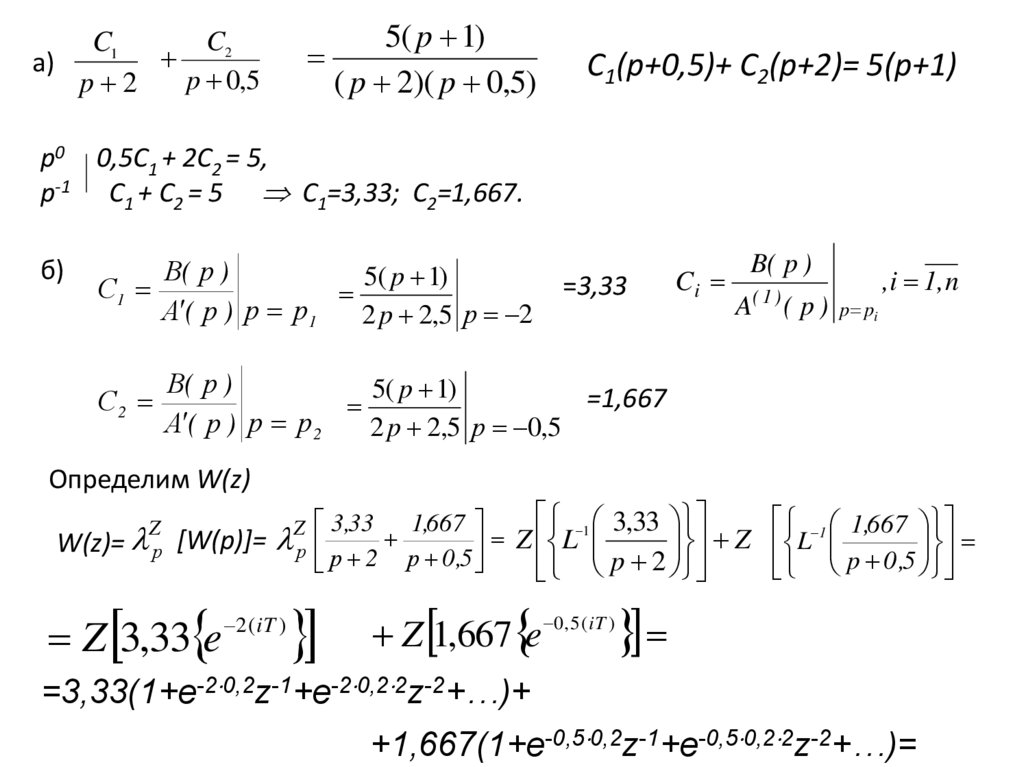












 Информатика
Информатика








