Теория графов. Способы задания графов. Визуализация графовых моделей

1.

ИНФОРМАТИКА
ТЕМА: ТЕОРИЯ ГРАФОВ. СПОСОБЫ ЗАДАНИЯ ГРАФОВ.
ВИЗУАЛИЗАЦИЯ ГРАФОВЫХ МОДЕЛЕЙ
Теплякова А.В.,
преподаватель информатики
ГБПОУ МО «Колледж «Коломна»

2.

И Н ТЕЛЛЕК ТУА ЛЬНА Я П РО Г РАММА У Ч ЕБНОГО З А Н Я ТИЯ :
1. Работа с основными понятиями
2. Структуры данных:
• Графы
• Деревья
• Таблицы
3. Использование графов на практике
ОЖ И ДАЕМ ЫЙ Р Е ЗУЛЬТАТ:
• знать классификацию графов
• знать способы задания графов
• уметь работать с графовыми моделями

3.

Живительная красота графов заключается в их простоте — они состоят лишь из точек и
линий, соединяющих эти точки. Но по-настоящему удивительно то, чего можно достичь с
помощью анализа этих точек и линий.
Графы возникают там, где между данными существуют какие-либо нелинейные связи.
Например, это могут быть компьютеры, соединённые в сеть, схема метро, модели
кристаллических решеток, карты местности, геометрические фигуры и т.д.

4.

Графы
Города Юго-Востока
Московской области:
• Коломна
• Луховицы
• Зарайск
• Озёры
• Ступино
• Серебряные Пруды

5.

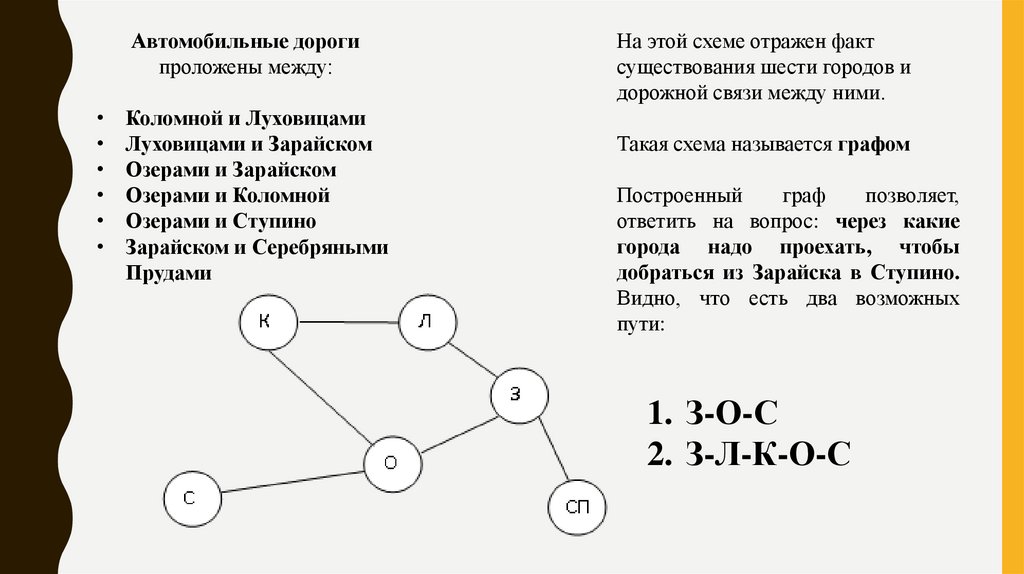
Автомобильные дороги
проложены между:
Коломной и Луховицами
Луховицами и Зарайском
Озерами и Зарайском
Озерами и Коломной
Озерами и Ступино
Зарайском и Серебряными
Прудами
На этой схеме отражен факт
существования шести городов и
дорожной связи между ними.
Такая схема называется графом
Построенный
граф
позволяет,
ответить на вопрос: через какие
города надо проехать, чтобы
добраться из Зарайска в Ступино.
Видно, что есть два возможных
пути:
1. З-О-С
2. З-Л-К-О-С

6.

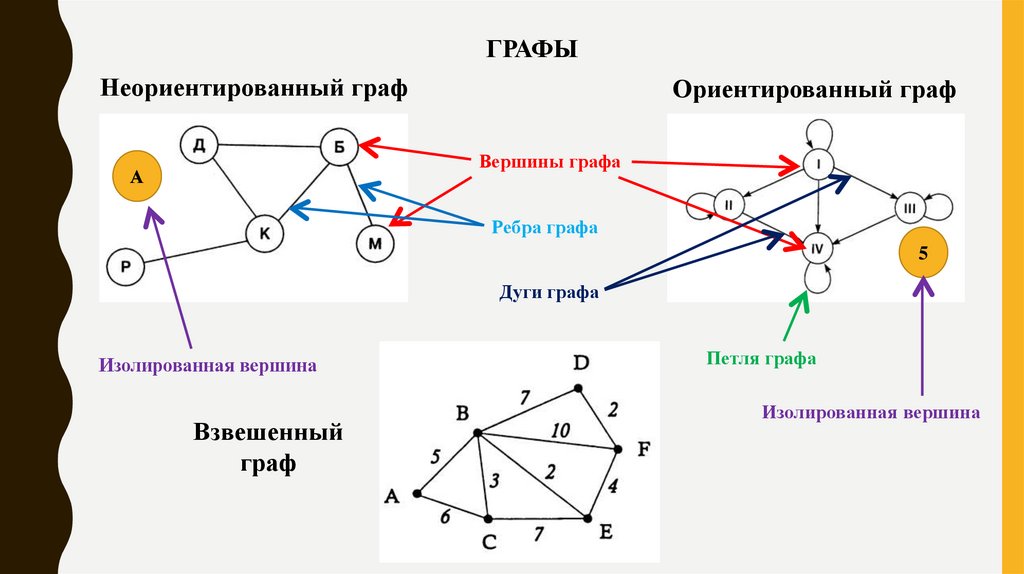
ГРАФЫ
Неориентированный граф
Ориентированный граф
Вершины графа
А
Ребра графа
5
Дуги графа
Изолированная вершина
Взвешенный
граф
Петля графа
Изолированная вершина

7.

Граф [graph - от греч. - пишу, изображаю] – это средство для наглядного представления
состава и структуры системы.
Существуют ориентированные и неориентированные графы.
Вершины графа – это компоненты системы, изображаемые точками, кружками, овалами,
прямоугольниками и пр.
Изолированные вершины - вершины, которым не соответствует ни одно ребро.
Ребра – это ненаправленные линии, связывающие между собой вершины.
Дуги – это направленные линии (стрелки), связывающие между собой вершины.
Петля – это ребро, соединяющее вершину с нею самой.
Сеть – связный граф без петель с выделенными вершинами.
Взвешенный граф – это граф, ребрам которого сопоставлены числа.
Длина пути во взвешенном графе - это сумма длин (весов) тех ребер, из которых состоит путь.

8.

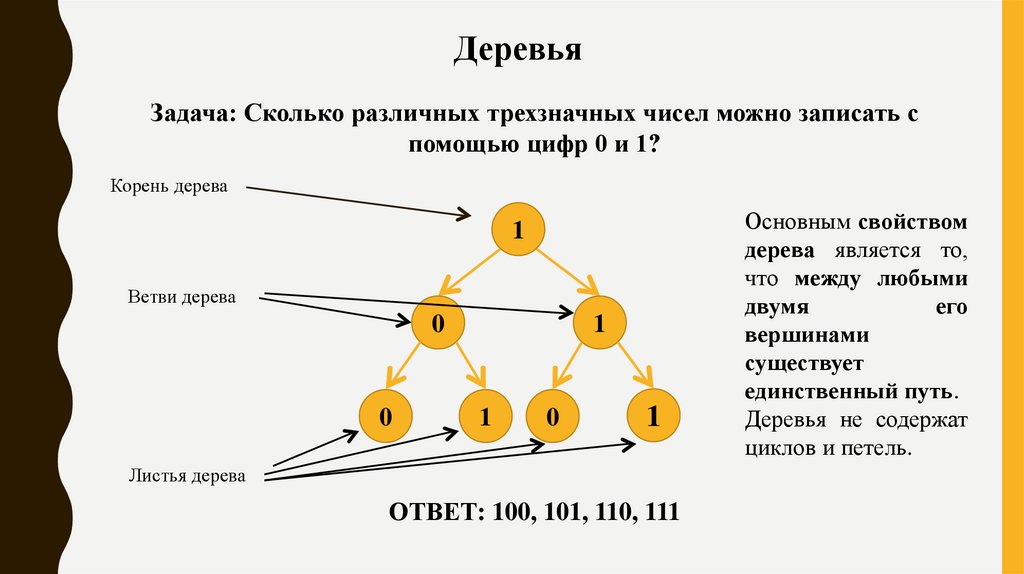
Деревья
Задача: Сколько различных трехзначных чисел можно записать с
помощью цифр 0 и 1?
Корень дерева
1
Ветви дерева
0
0
1
1
0
1
Листья дерева
ОТВЕТ: 100, 101, 110, 111
Основным свойством
дерева является то,
что между любыми
двумя
его
вершинами
существует
единственный путь.
Деревья не содержат
циклов и петель.

9.

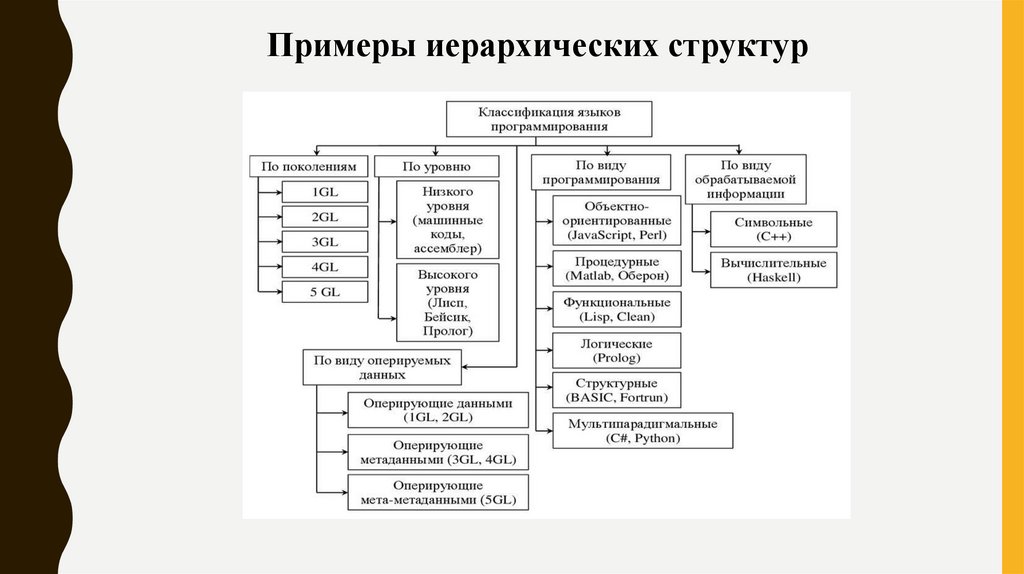
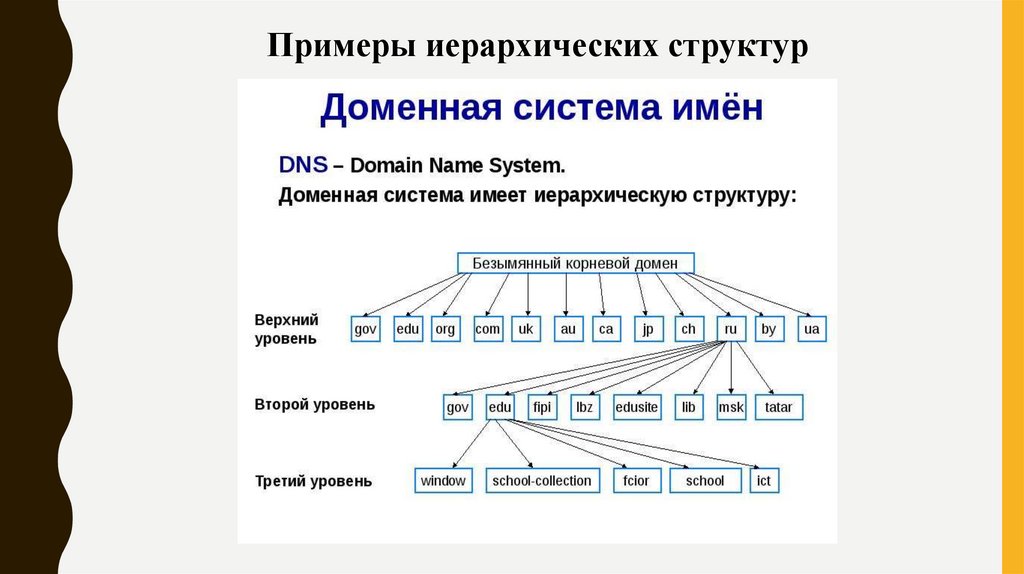
Примеры иерархических структур

10.

Примеры иерархических структур

11.

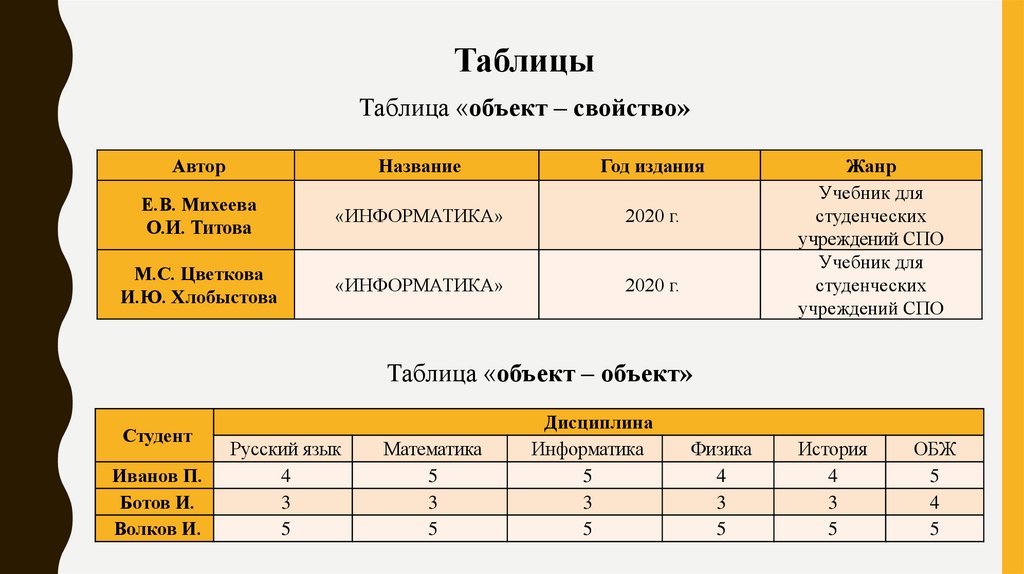
Таблицы
Таблица «объект – свойство»
Автор
Название
Год издания
Е.В. Михеева
О.И. Титова
«ИНФОРМАТИКА»
2020 г.
М.С. Цветкова
И.Ю. Хлобыстова
«ИНФОРМАТИКА»
2020 г.
Жанр
Учебник для
студенческих
учреждений СПО
Учебник для
студенческих
учреждений СПО
Таблица «объект – объект»
Студент
Иванов П.
Ботов И.
Волков И.
Русский язык
4
3
5
Математика
5
3
5
Дисциплина
Информатика
5
3
5
Физика
4
3
5
История
4
3
5
ОБЖ
5
4
5

12.

Двоичные матрицы (матрицы смежности)

13.

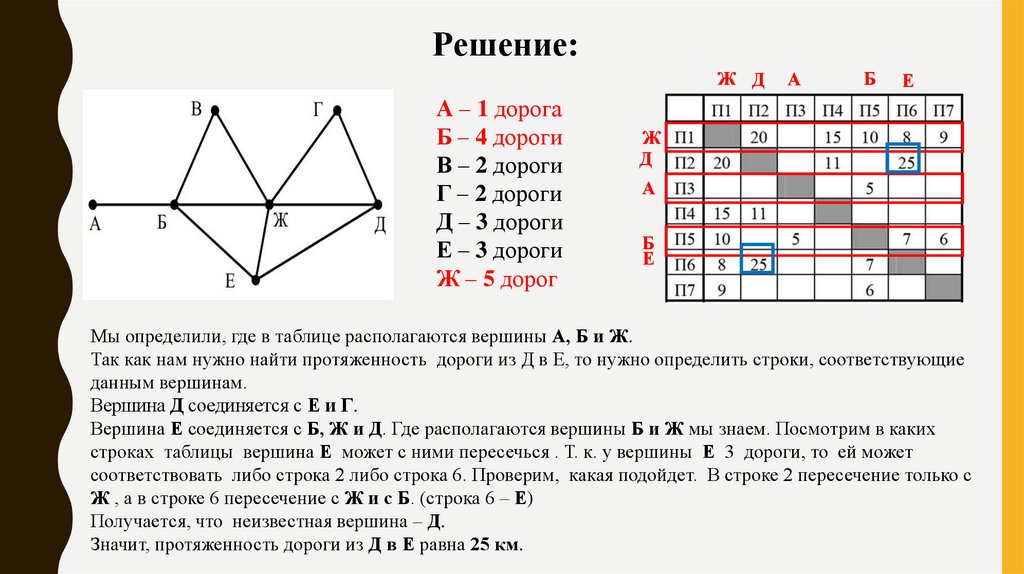
Решение:
Ж Д
А – 1 дорога
Б – 4 дороги
В – 2 дороги
Г – 2 дороги
Д – 3 дороги
Е – 3 дороги
Ж – 5 дорог
А
Б
Е
Ж
Д
А
Б
Е
Мы определили, где в таблице располагаются вершины А, Б и Ж.
Так как нам нужно найти протяженность дороги из Д в Е, то нужно определить строки, соответствующие
данным вершинам.
Вершина Д соединяется с Е и Г.
Вершина Е соединяется с Б, Ж и Д. Где располагаются вершины Б и Ж мы знаем. Посмотрим в каких
строках таблицы вершина Е может с ними пересечься . Т. к. у вершины Е 3 дороги, то ей может
соответствовать либо строка 2 либо строка 6. Проверим, какая подойдет. В строке 2 пересечение только с
Ж , а в строке 6 пересечение с Ж и с Б. (строка 6 – Е)
Получается, что неизвестная вершина – Д.
Значит, протяженность дороги из Д в Е равна 25 км.

14.

Лист самооценки
Моя успешность на уроке
1. Материал урока мне был
понятен и интересен
2. Результат соответствует моим
ожиданиям
3. Урок показался
длинным/коротким
4. За урок я устал(а)/не устал(а)
5. Для чего мне нужен материал,
полученный на уроке
ТВОРЧЕСКИХ УСПЕХОВ!