Графы. Степень вершины. Подсчет числа ребер графа

1.

Графы
Степень вершины
Подсчет числа ребер графа

2.

Разминка…
Вставьте недостающие слова в предложения
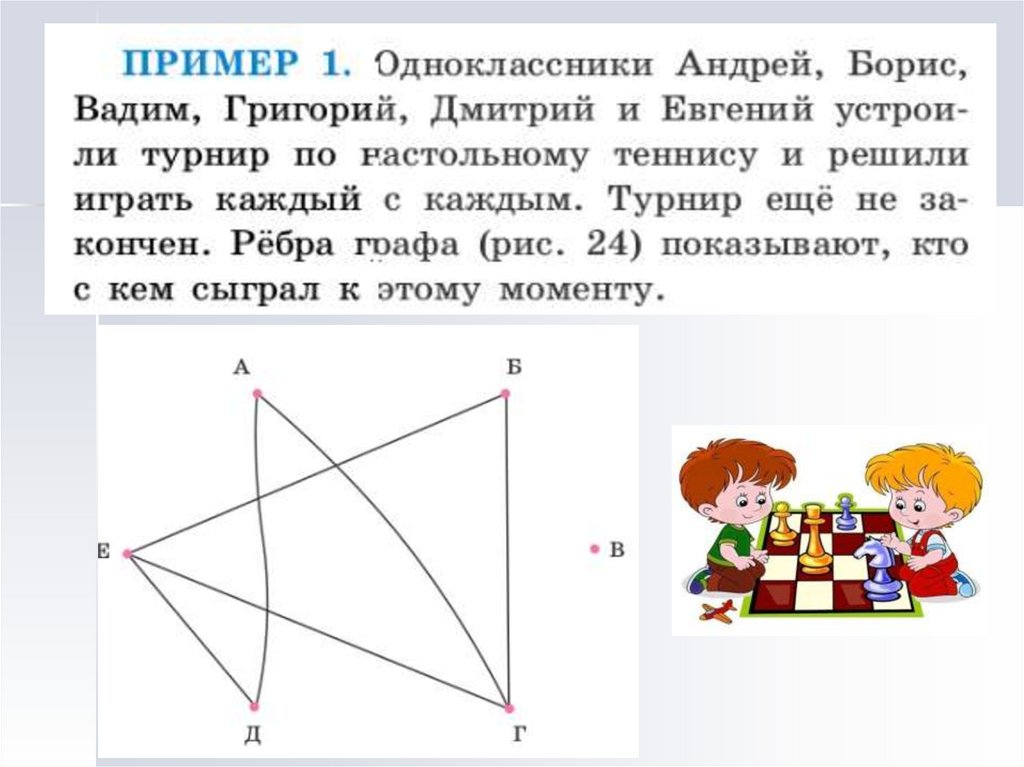
Всем известно, что слово «граф» означает дворянский
титул, например,граф Лев Николаевич Толстой. А вот в
титул
математике …
Граф – это изображение объектов и связей между
ними с помощью точек и линий.

3.

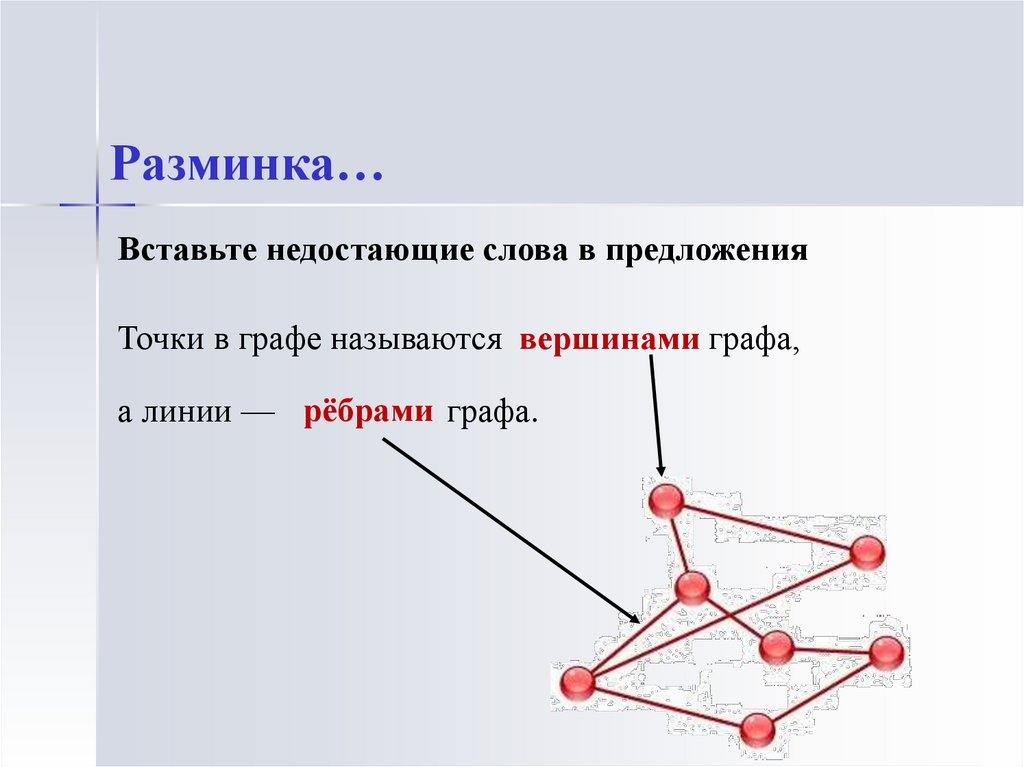
Разминка…
Вставьте недостающие слова в предложения
Точки в графе называются вершинами графа,
а линии — рёбрами графа.

4.

Разминка…
Вставьте недостающие слова в предложения
Вершину, из которой не выходит ни
одно ребро, называют изолированной

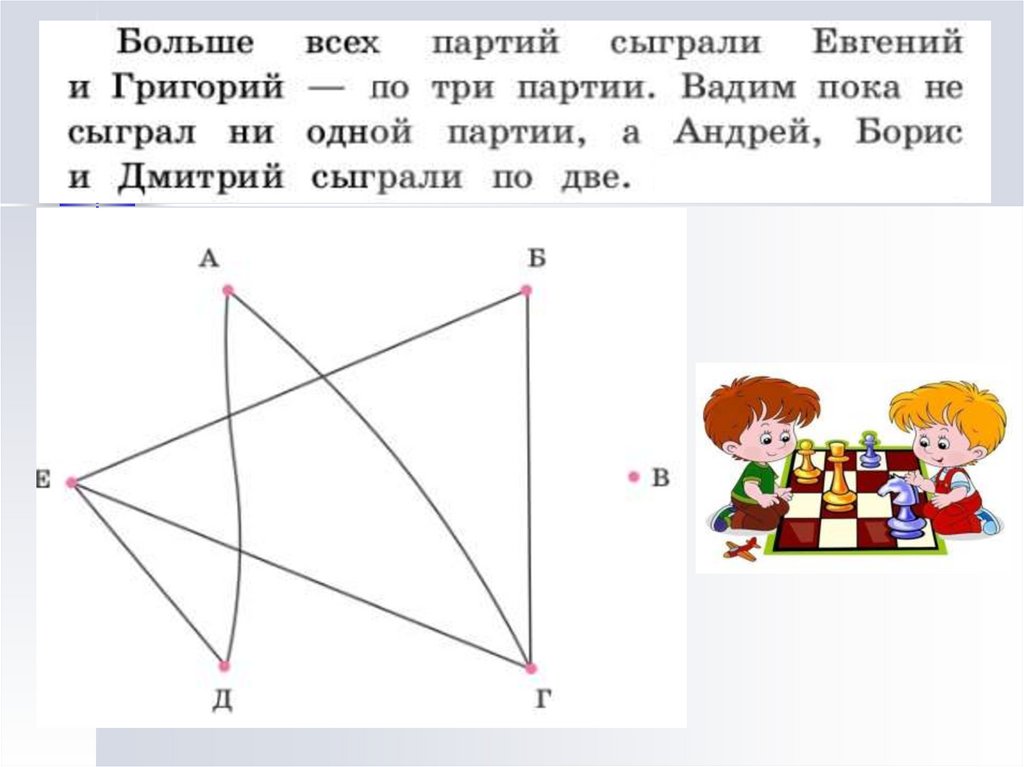
5. В стране Знак есть 9 городов с названиями 1, 2, 3, 4, 5, 6, 7, 8, 9. Путешественник обнаружил, что два города соединены дорогой

Выполните задание
В стране Знак есть 9 городов с названиями
1, 2, 3, 4, 5, 6, 7, 8, 9.
Путешественник обнаружил, что два
города соединены дорогой в том и только
в том случае, если двузначное число,
образованное названиями городов, делится
на 3.

6.

Выполните задание
Постройте граф, обозначив вершины графа
цифрами (названия городов).
Соедините ребрами те вершины, которые
удовлетворяют условию задачи.
Посчитайте количество ребер.
Можно ли долететь по воздуху из города 1
в город 9 ?

7.

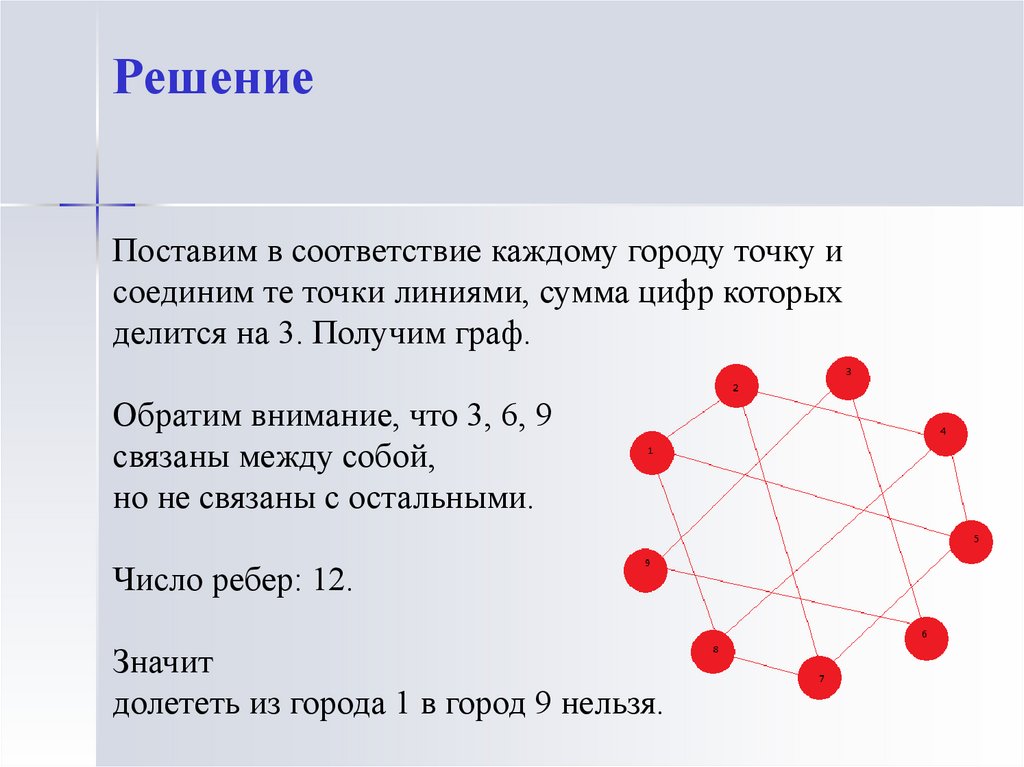
Решение
Поставим в соответствие каждому городу точку и
соединим те точки линиями, сумма цифр которых
делится на 3. Получим граф.
Обратим внимание, что 3, 6, 9
связаны между собой,
но не связаны с остальными.
Число ребер: 12.
Значит
долететь из города 1 в город 9 нельзя.

8.

9.

10.

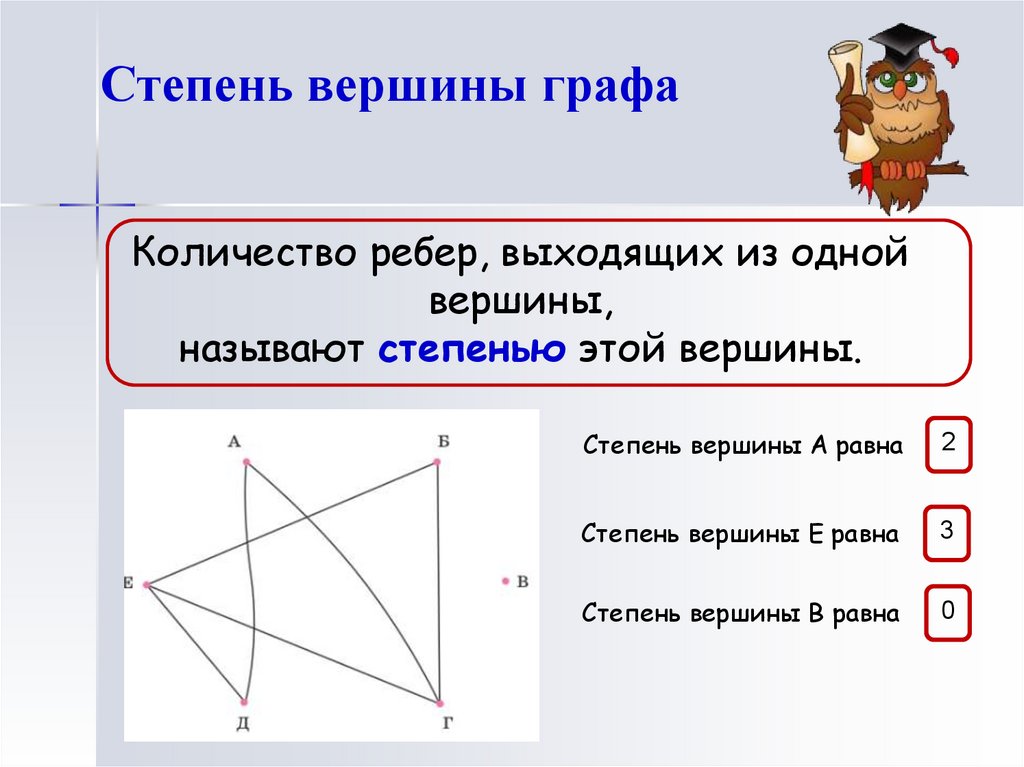
Степень вершины графа
Количество ребер, выходящих из одной
вершины,
называют степенью этой вершины.
Степень вершины А равна
2
Степень вершины Е равна
3
Степень вершины В равна
0

11.

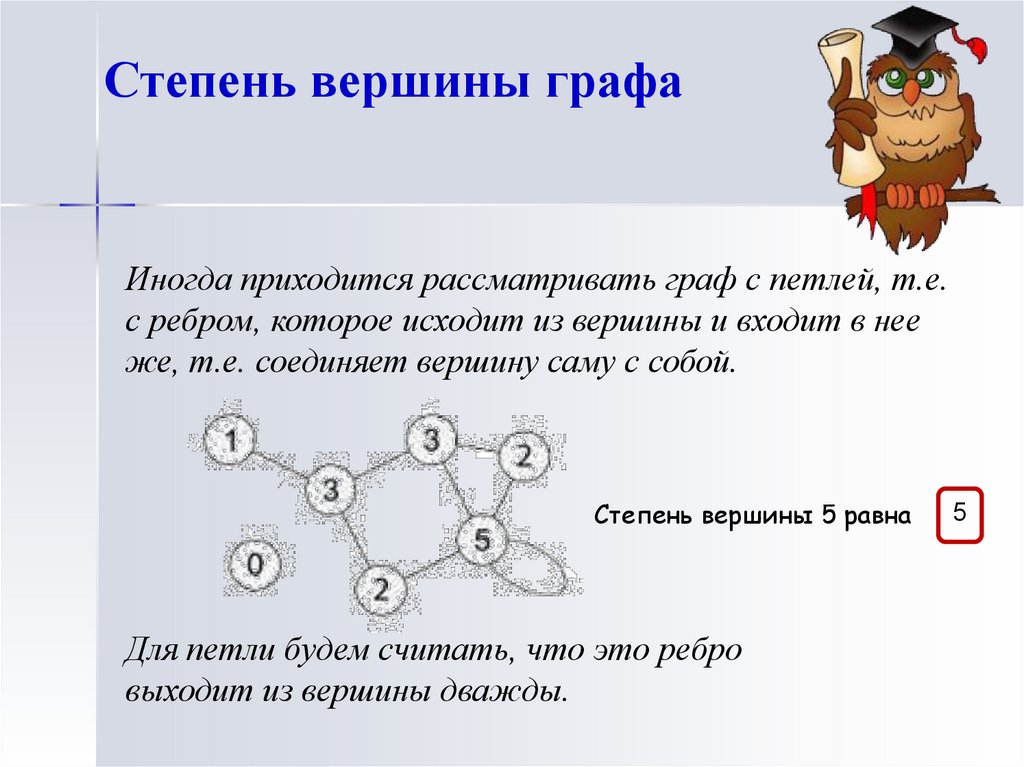
Степень вершины графа
Иногда приходится рассматривать граф с петлей, т.е.
с ребром, которое исходит из вершины и входит в нее
же, т.е. соединяет вершину саму с собой.
Степень вершины 5 равна
Для петли будем считать, что это ребро
выходит из вершины дважды.
5

12.

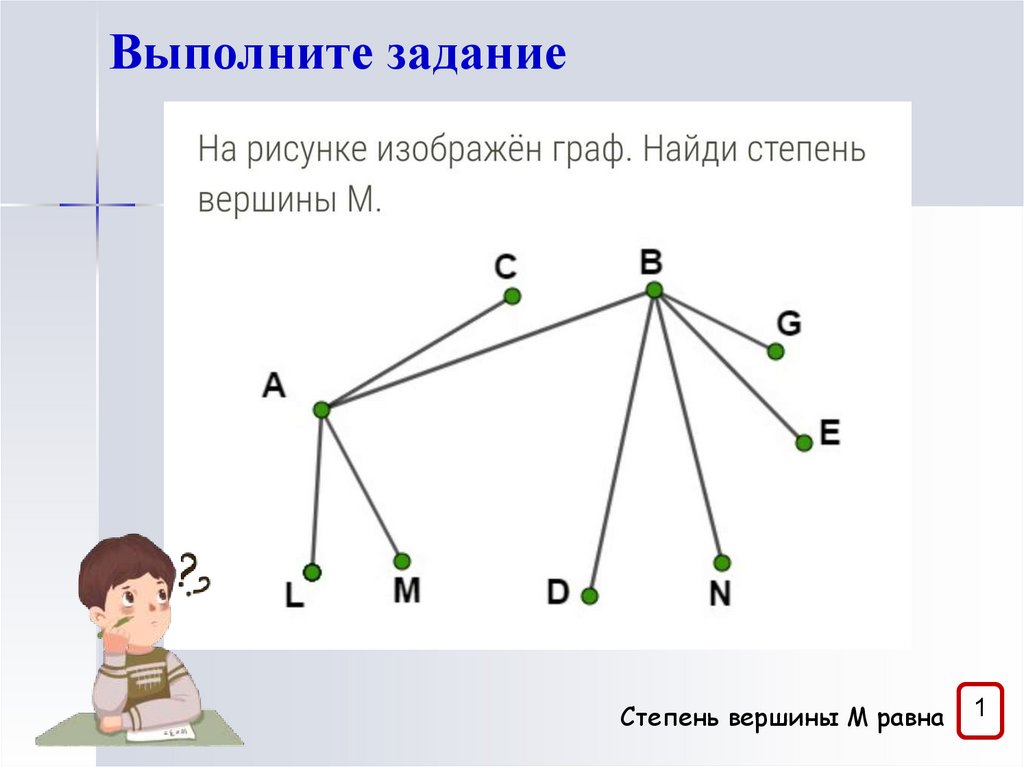
Выполните задание
Степень вершины М равна
1

13.

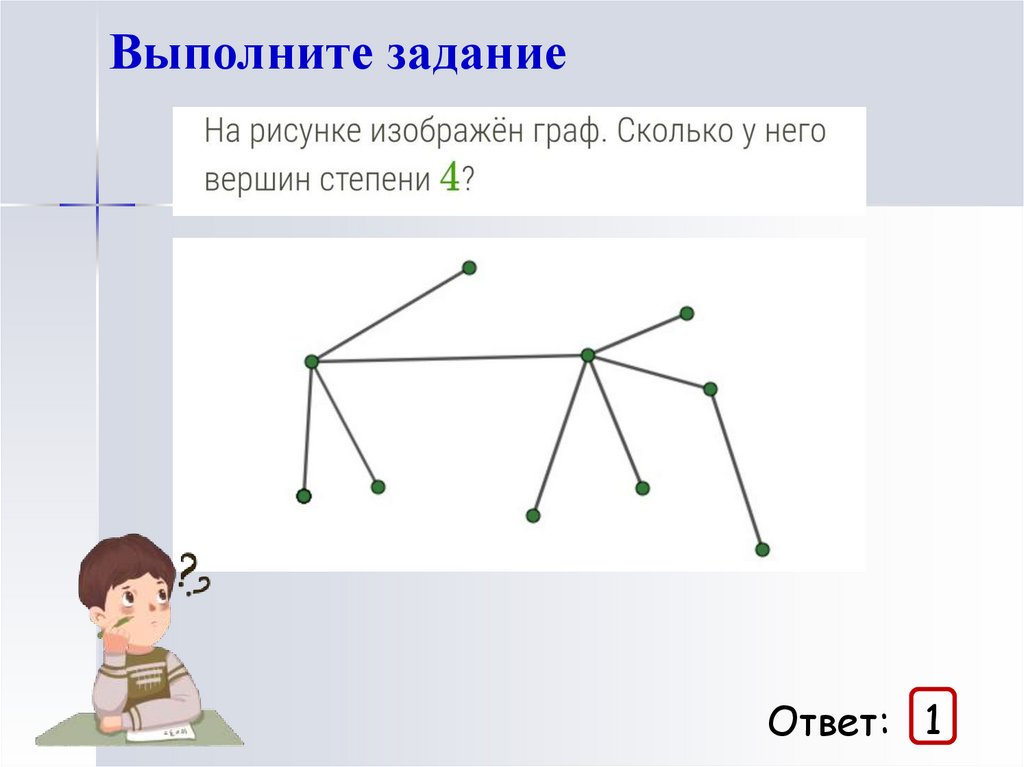
Выполните задание
Ответ: 1

14.

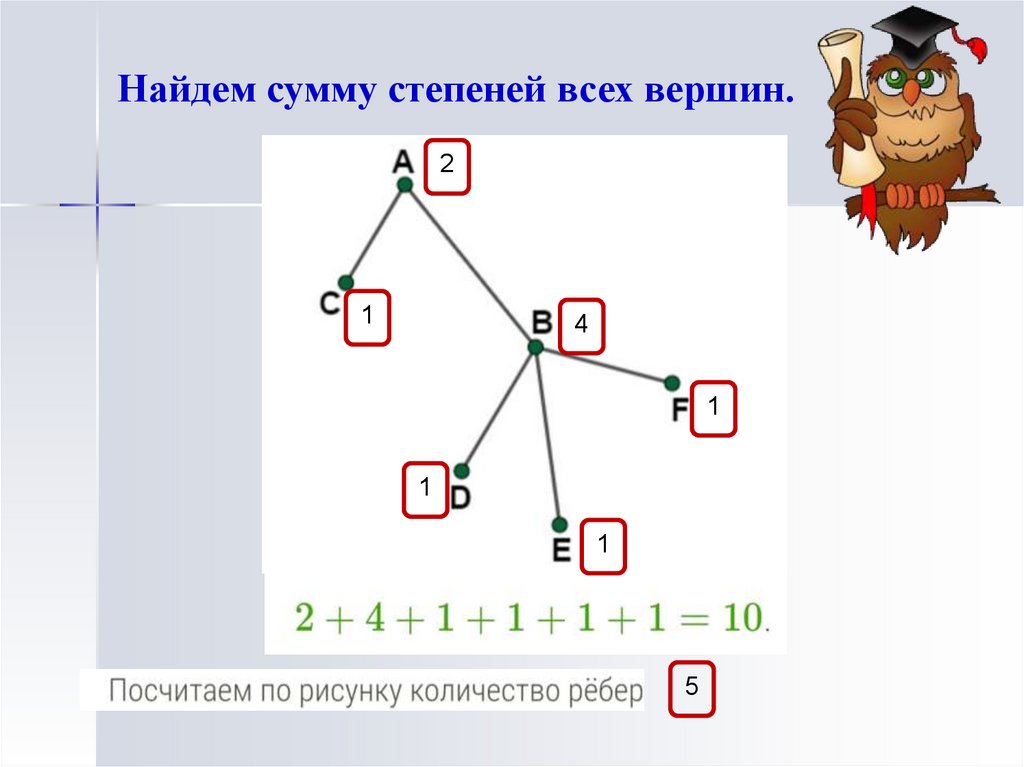
Найдем сумму степеней всех вершин.
2
1
4
1
1
1
5

15.

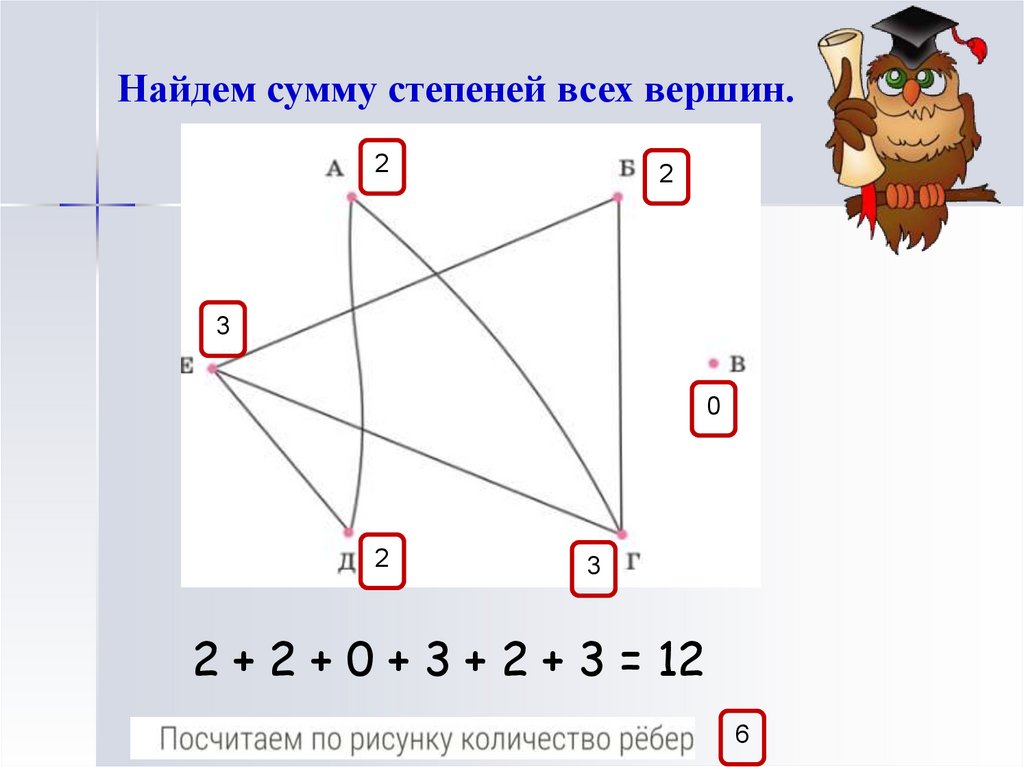
Найдем сумму степеней всех вершин.
2
2
3
0
2
3
2 + 2 + 0 + 3 + 2 + 3 = 12
6

16.

Правило
Чтобы найти количество рёбер, нужно сумму
степеней его вершин разделить пополам.
2 + 2 + 0 + 3 + 2 + 3 = 12
Количество ребер:
12 : 2 = 6

17.

Теорема о сумме степеней
всех вершин
В любом графе сумма степеней всех вершин
является чётным числом.

18.

Выполните задание
6 + 1 + 8 + 8 + 15 = 38
Количество ребер:
38 : 2 = 19
Ответ: 19

19.

Количество вершин нечетной степени
4
2
Количество вершин четной степени
2
3

20.

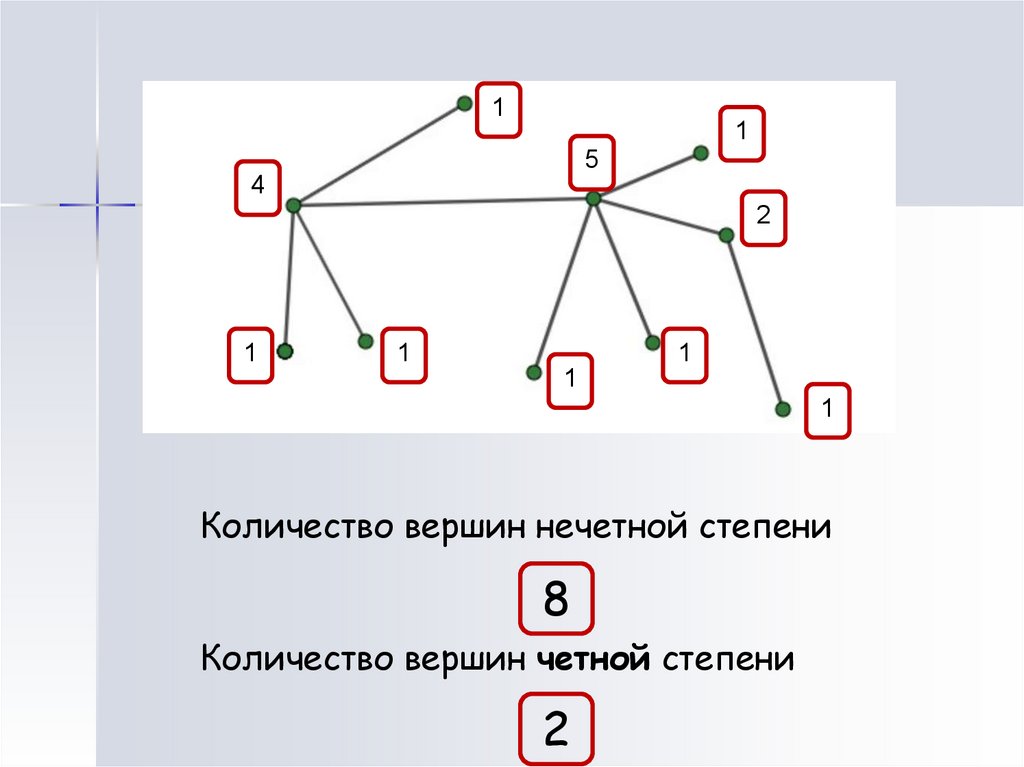
1
1
5
4
2
1
1
1
1
1
Количество вершин нечетной степени
8
Количество вершин четной степени
2

21.

Вывод
В любом графе количество вершин
нечетной степени чётно.