Модели ценообразования

1. Пример 2

• Стоимость компании без долговых
обязательств V=10 млн.
• Компания собирается эмитировать долговые
обязательства номинальной стоимостью
F=7 млн. со сроком погашения через T=10 лет.
• Стандартное отклонение доходности
компании σ=0,6324, безрисковая ставка - 10%
(r=0,1).
Определить стоимость собственного капитала
компании.

2. Модели ценообразования

3. Список литературы

• Брусов П.Н., Филатова Т.В., Лахметкина Н.И.
Инвестиционный менеджмент: Учебник, М.:
ИНФРА-М, 2014. – 333 с.
• Хамедшин Д.Р. К вопросу об использовании
моделей ценообразования активов в анализе
эффективности реальных инвестиций // Российский
экономический интернет-журнал [Электронный
ресурс]. – М.: АТиСО, 2009. – Режим доступа:
http://www.e-rej.ru/Articles/2009/Khametshin.pdf
• Сысоев А. Ю. Использование моделей «реальных
опционов» при оценке эффективности
инвстиционных проектов // ВЕСТНИК ФА, 2003, №4. – 110-120

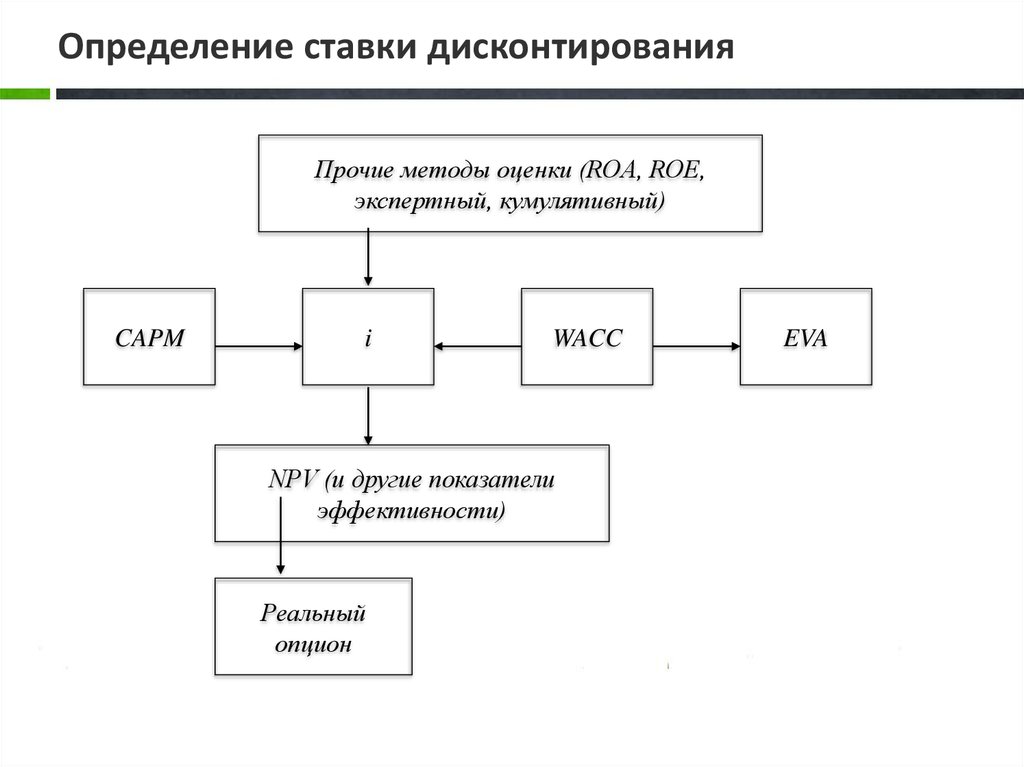
4. Определение ставки дисконтирования

Прочие методы оценки (ROA, ROE,
экспертный, кумулятивный)
CAPM
i
WACC
NPV (и другие показатели
эффективности)
Реальный
опцион
EVA

5.

CAPM
EVA
Real Option

6. CAPM

Модель основана на портфельной
теории Г. Марковица
Основоположники:
У. Шарп, Дж. Линтер, Я. Моссин,
Дж.Трейнер
Capital Asset Price Model
модель ценообразования финансовых активов

7. У. Шарп (William Sharpe) – Нобелевская премия по экономике 1990

8. Модель оценки финансовых активов

• ожидаемый доход, который потребуют
инвесторы, равен ставке по безрисковой
ценной бумаге + рисковой премии.
• Если ожидаемый риск не равен или выше,
чем требуемая доходность, то инвесторы
откажутся инвестировать, и инвестиции не
будут сделаны.
• Выделены систематический и
специфический риск.

9. Допущения модели CAPM

1) Эффективный финансовый рынок, доступность
информации, рациональное поведение
инвесторов
2) Отсутствие транзакционных издержек
3) Стремление инвесторов к максимизации
ожидаемой доходности при минимизации рисков
4) Одинаковый период вложения для инвесторов
5) Делимость и ликвидность финансовых
инструментов
6) Несущественные налоги и операционные
издержки
7) Кредитование и заимствования по безрисковой
ставке при возможности рисковых инвестиций
8) Одинаковая безрисковая ставка для всех
инвесторов

10. Следствия модели

• Модель на один период
• Нормальное распределение Гаусса
• Отсутствие человеческого капитала (т.к. он
неделим)
• Инвестиции в индивидуальные ценные
бумаги бесполезно; формирование
портфелей из дешевых индексных фондов

11. Систематический vs специфического риска

• Систематический (рыночный /
недиверсифицируемый) риск – это риск, который
характерен для всех ценных бумаг и не может быть
устранен за счет диверсификации. Систематический
риск обусловлен общим движением рынка или его
сегментов и не связан с конкретной ценной бумагой.
• Специфический (несистематический) риск – риск,
являющийся результатом состояния отдельной отрасли,
предприятия, типа инвестиционного процента. Связан с
внутренними факторами деятельности эмитента акций
или инвестора, отрицательно воздействующими на
эффективность инвестирования. Может быть устранен
диверсификацией.

12. Модель ценообразования капитальных активов (CAPM)

Re = Rf + b * (Rm - Rf )
где Re – ожидаемая доходность на актив (цена капитала,
привлекаемого за счет обыкновенных акций);
Rf – безрисковая составляющая доходности;
Rm - ожидаемая средняя доходность рыночного портфеля
(индекса);
β-коэффициент чувствительности ценной бумаги к
изменению средней доходности портфеля (индекса).

13. Систематический риск (β-коэффициент)

Cov(ri , rm )
bi =
Var(rm )
Cov(ri, rm) – функции ковариации; Var (rm) – функция дисперсии;
n
Cov (ri , rm )
(r r ) (r
i
i 1
n 1
(r
m
Var (rm )
m
rm)
n
2
rm )

14. β - риск

• β - совокупный риск от инвестирования в
общий рынок: на Нью-Йоркской фондовой
бирже β =1.
• β компании - риск компании по сравнению
с риском общего рынка. Beta показывает
волатильность ценной бумаги,
относительно типа актива. Если компания
имеет Beta 3.0, то предполагается, что ее активы
в 3 раза более рискованны, чем общий рынок.

15. Модель CAPM для реальных проектов

NPV = P(X) – I
P(X) – случайная величина будущего дохода, распределяемая
среди инвесторов;
I – инвестиционные затраты нулевого периода.
P(X) =
X
X
=
1+ rx 1+ rf + b x (rm - rf )
X – ожидаемый будущий доход; rx – ожидаемая доходность
от инвестиций с аналогичным уровнем риска.

16. Пример 1

Пусть в рамках однопериодной экономики неопределенность
характеризуется двумя потенциальными состояниями: u, d.
Вероятность реализации событий:
π(u)=0,7 и π (d)=0,3.
Случайная доходность рыночного портфеля задана
следующим распределением:
rm(u) =15% и rm(d)=3%.
rf = 5% (безрисковая ставка);
I = 70 тыс. руб.
X(u) = 100 тыс. руб.; X(d) = 80 тыс. руб.
Оценить инвестиционную привлекательность
проекта с помощью критерия NPV.

17. Алгоритм решения

1) Находим чистую доходность rx в каждом
будущем моменте времени.
X
rx = -1
I
1) Оценим ожидаемую доходность rx от
финансовых инвестиций с аналогичным
уровнем риска, исходя из CAPM.
2) Рассчитаем ожидаемый доход проекта X и
его NPV.

18.

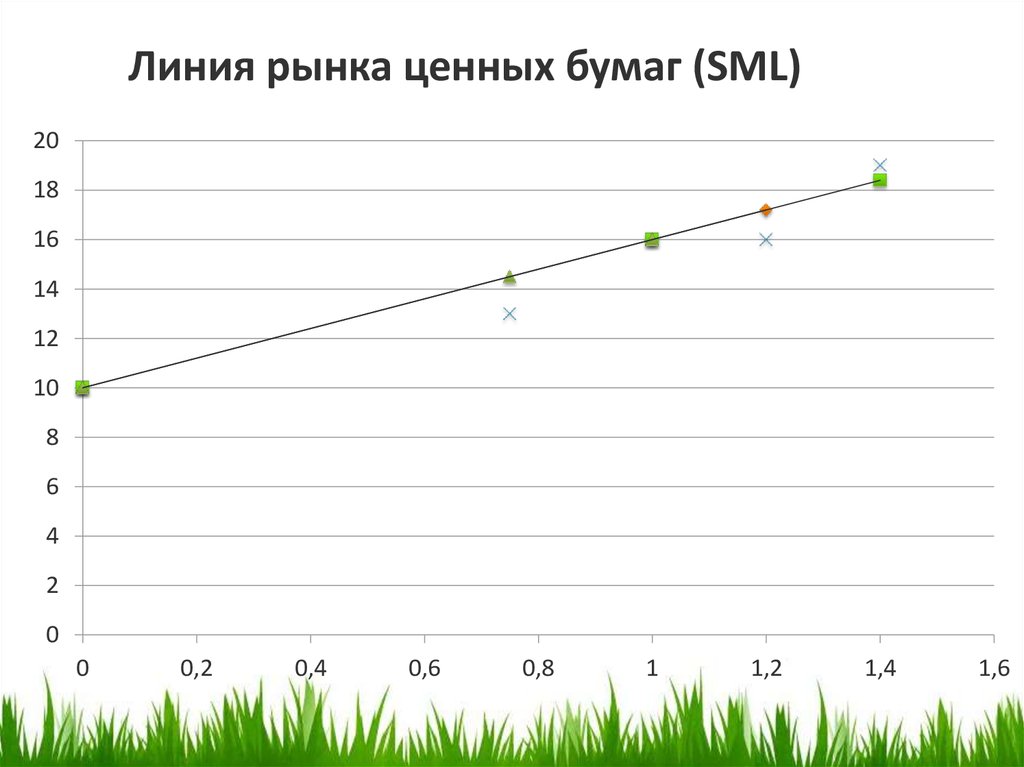
19. Пример 2

Текущая рыночная доходность rm =16%, а безрисковая
ставка rf =10%.
Вид актива
А
В
С
Доходность акции
16%
19%
13%
β
1,2
1,4
0,75
Вопрос:
а) Какие из акций являются переоцененными согласно
САРМ?
б) Какие из акций являются недооцененными
согласно САРМ?
в) Постройте линию рынка ценных бумаг.

20.

Линия рынка ценных бумаг (SML)
20
18
16
14
12
10
8
6
4
2
0
0
0,2
0,4
0,6
0,8
1
1,2
1,4
1,6

21. Альтернативы модели CAPM

1) Факторные модели (i =1, 2, 3…, n)
ri ai bi f i
ri ai bi1 f1 bi 2 f 2 i
2) Теория арбитражного ценообразования
Росса (APT)
Основное предположение: каждый инвестор стремится
увеличить доходность портфеля без увеличения риска
ri ai bi f
Возможные факторы: индекс промышленного
производства, инфляция, краткосрочная реальная ставка
процентов, риск неуплаты по облигациям

22. Альтернативные CAPM модели

3) Модель Ольсона (EBO - Edwards-Bell-Ohlson
valuation model)
Стоимость компании (Pt) – текущая стоимость чистых
активов и дисконтированный поток «сверхдоходов»
(отклонений прибыли от средней по отрасли).
E – ожидаемые значения;
ROE – рентабельность акционерного капитала;
Bt – стоимость чистых активов (балансовая стоимость)
re – цена акционерного капитала

23. EVA

Разработан
Д. Стерном и Б. Стюартом
Economic Value Added
Экономическая добавленная стоимость

24. EVA

• показатель экономической добавленной стоимости,
определяемой как разница между чистой операционной
прибылью и стоимостью использования капитала
(собственного и заемного)
EVA NOPAT IC WACC
EVA IC ( ROIC WACC )
где NOPAT – чистая операционная прибыль после уплаты налогов;
IC – объем инвестированного капитала;
WACC – средневзвешенная стоимость капитала;
ROIC – рентабельность инвестированного капитала.

25. Особенности

1) организация рассматривается подобно
инвестиционному проекту
2) эффективность инвестиций подтверждается
приростом стоимости организации
(неотрицательный показатель EVA).
3) Простота формулы
4) применение корректировок капитала,
позволяющих сделать прибыль организации
ближе к денежному потоку, а капитал
выразить корректней.

26. Реальный опцион

27. Опцион

- договор, в соответствии с которым один из
его участников приобретает право покупки
или продажи какого-либо товара по
фиксированной цене в течение некоторого
периода времени, а другой участник за
денежную премию обязуется обеспечить при
необходимости реализацию этого права,
будучи готовым продать или купить ценные
бумаги по определенной договорной цене.

28. Развитие теории

• 1973 год
Фишер Блэк (Fisher Black), Майрон Шоулз
(Myron Scholes) и Роберт Мертон (Robert
Merton) - впервые предложили формулу
стоимостной оценки опциона колл
• 1984 год
Стюарт Майерс (Stewart Myers) и Карл Кестер
(Carl Kester)
Метод реальных опционов

29. Опционный контракт

• Опцион кол (call)
• Опцион пут (put)
• Покупатель (держатель опциона) - long
• Продавец (надписатеь опциона) - short

30.

Покупатель
Продавец
ПРАВО
ОБЯЗАТЕЛЬСТВО
Опцион
(long)
(short)
Call
↑X
↓Y
Put
↓Y
↑X

31. Пример торговли опционами на МосБирже

32. Реальный опцион

это право (и не обязанность) принять какое-либо
управленческое решение в процессе функционирования
компании, реализации инвестиционного проекта.

33. Виды реальных опционов

• Опцион на выбор времени принятия решения
об осуществлении капитальных инвестиций
• Опцион роста - дополнительные
возможности, которые могут появиться после
того как сделаны первоначальные инвестиции.
• Опцион изменения масштаба - увеличение
или сокращение масштабов производства в
течение жизненного цикла проекта.
• Опцион на отказ от реализации проекта отказ от наиболее нерентабельных проектов.

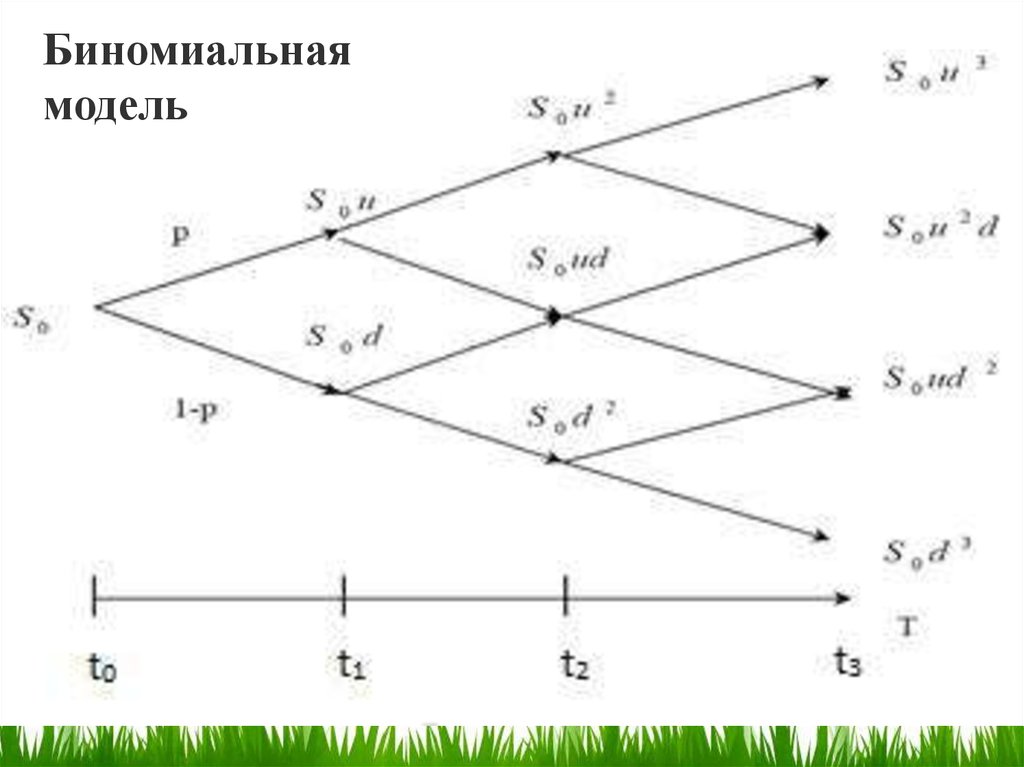
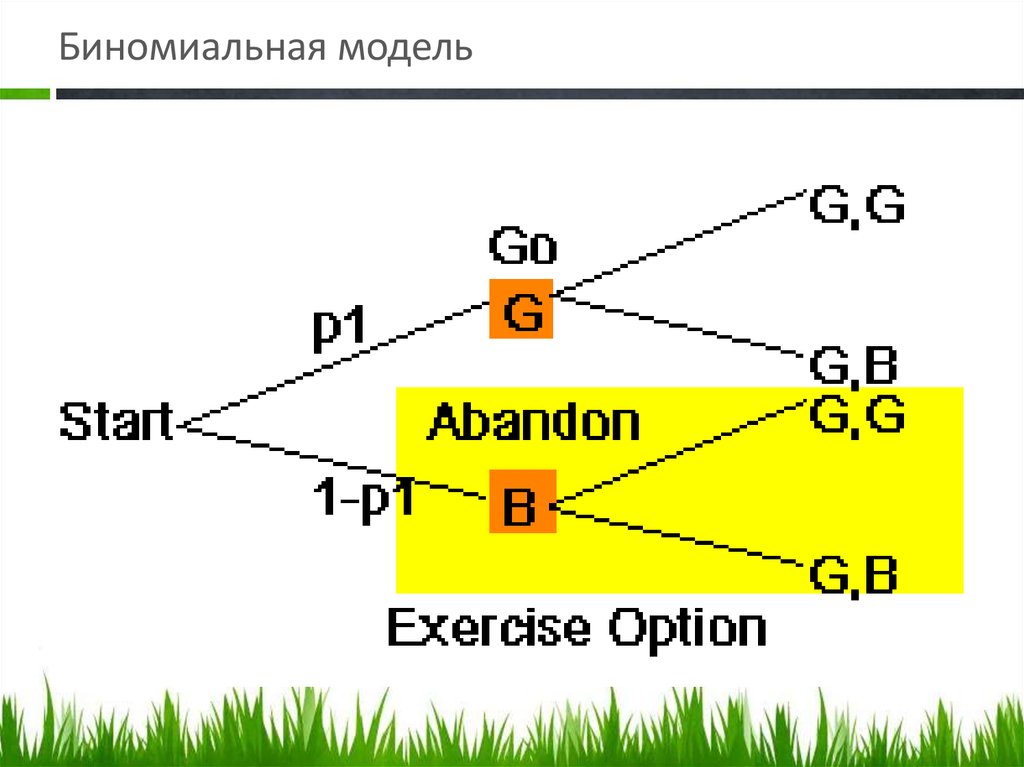
34. Методы оценки реальных опционов

1) Модель Блека-Шоулза
Black–Scholes Option Pricing Model (OPM)
1) Биномиальная модель
Д.Кокс, С.Росс, М. Рубинштейн

35. Модель Блэка-Шоулза

C0 S N (d1 )
x
t
1 r
S – рыночная цена базового актива; 365
N (d 2 )
Х – цена исполнения (цена актива по договору);
N(d1), N(d2) – вероятность того, что при нормальном
распределении со средней, равной нулю, и
стандартном отклонении, равном единице, результат
будет меньше d1 и d2
r – безрисковая процентная ставка
t - срок контракта в днях

36.

Цена опциона колл
C S N (d1 ) X e
r (T t )
N (d 2 )
Цена опциона пут
P X e r (T t ) N ( d 2 ) S N ( d1 )
S – рыночная цена базового актива;
Х – цена исполнения (цена актива по договору);
N(d1), N(d2) – вероятность того, что при нормальном распределении со
средней, равной нулю, и стандартном отклонении, равном единице, результат
будет меньше d1 и d2
r – безрисковая процентная ставка
T-t - срок контракта
e=2,7183

37.

d1
d2
ln( s / х) (r
2
2
)t
t
ln( s / х) (r
T
ln( s / х) rt
t
1
t
2
2
2
)t
d1 t
σ - стандартное отклонение цены акции, которое берется в
годовом исчислении в относительных единицах.

38. Волатильность

• стандартное отклонение цены от среднего
1 п
2
( хi m)
n 1 i 1
• m - среднее значение случайной величины (цены
акций);
• n - число наблюдений;
• хi - значение случайной величины в каждом
наблюдении.

39. Пример 1

S0 - цена базового актива (текущая стоимость
денежных потоков от инвестиций) – 200 млн. руб.
X –цена исполнения (размер инвестиций) – 250 млн.
руб.
σ –волатильность (среднеквадратическое отклонение
денежных потоков) – 30%
r – безрисковая ставка доходности (доходность
государственных облигаций) – 5%
T – время истечения срока (длительность периода, на
который может быть отложено принятие решения) – 3
года
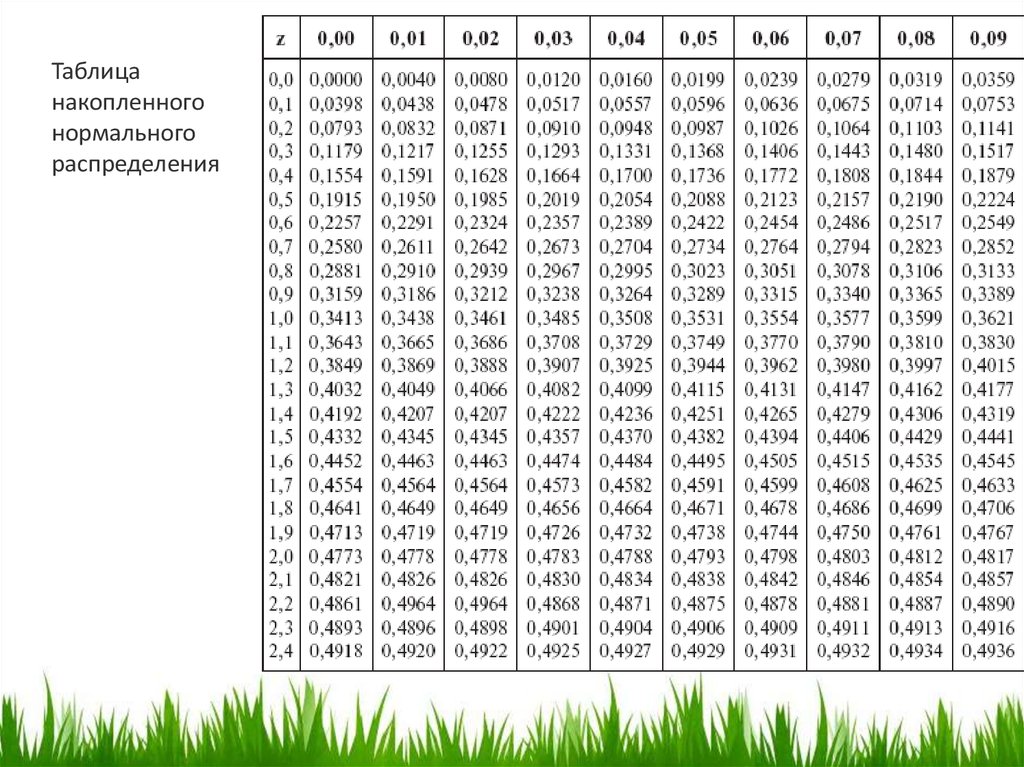
N(d) – кумулятивная функция нормального
распределения

40. Решение

d1=[ln(S0/X)+(r+0.5σ2)T]/σ√T
=[ln(100/200)+(0.05+0.5∗0.32)3]/(0.3∗ √3) =0.119
d2= d1− σ√T = 0.119 − 0.3 ∗ √3 = −0.551
N(d1) = 0.547
N(d2) =0.290
С=N(d1)S0−N(d2)