Решение задач ОГЭ по математике «Окружность и ее элементы»

1. Подготовка к ОГЭ

Решение задач ОГЭ по теме
«Окружность и ее
элементы»

2. Задания части 1.

Подготовка к ОГЭ
Задания части 1.

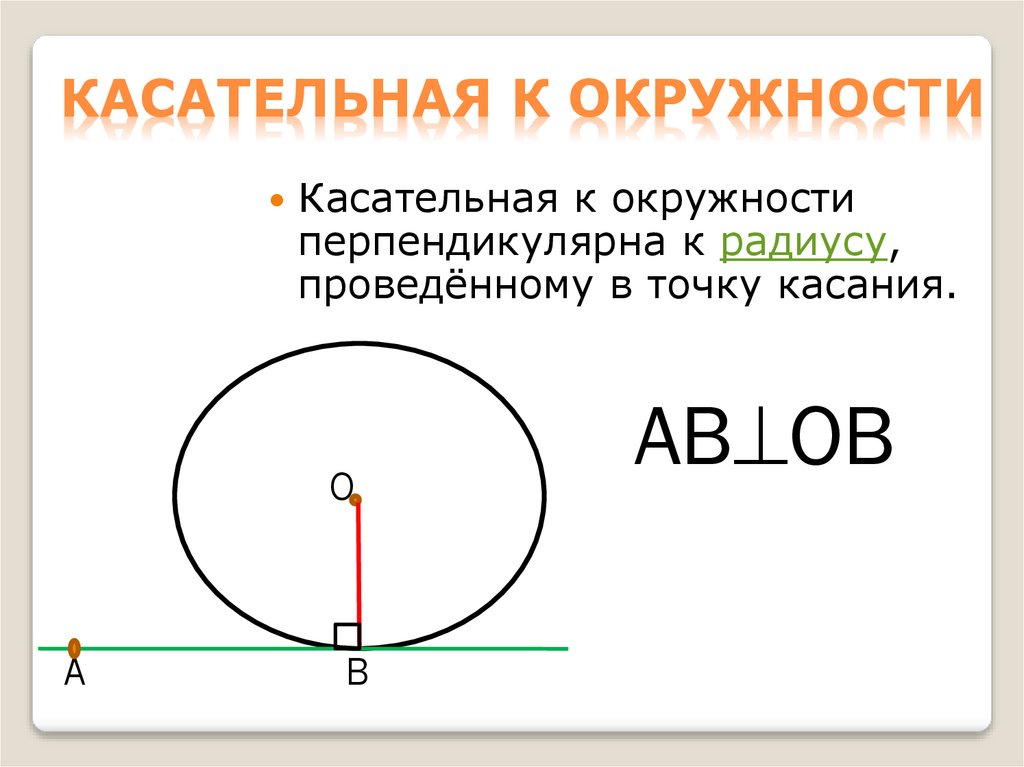
3. Касательная к окружности

КАСАТЕЛЬНАЯ К ОКРУЖНОСТИ
Касательная к окружности
перпендикулярна к радиусу,
проведённому в точку касания.
О
А
В
АВ ОВ

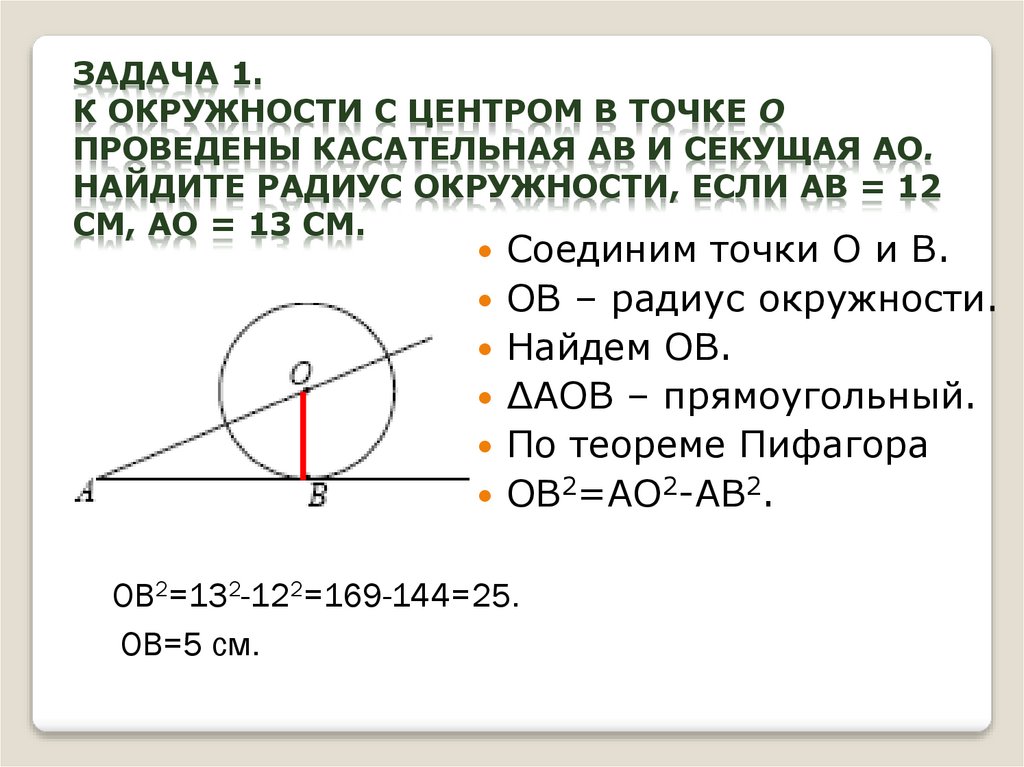
4. Задача 1. К окружности с центром в точке О проведены касательная AB и секущая AO. Найдите радиус окружности, если AB = 12 см,

ЗАДАЧА 1.
К ОКРУЖНОСТИ С ЦЕНТРОМ В ТОЧКЕ О
ПРОВЕДЕНЫ КАСАТЕЛЬНАЯ AB И СЕКУЩАЯ AO.
НАЙДИТЕ РАДИУС ОКРУЖНОСТИ, ЕСЛИ AB = 12
СМ, AO = 13 СМ.
Соединим точки О и В.
ОВ – радиус окружности.
Найдем ОВ.
∆АОВ – прямоугольный.
По теореме Пифагора
ОВ2=АО2-АВ2.
ОВ2=132-122=169-144=25.
ОВ=5 см.

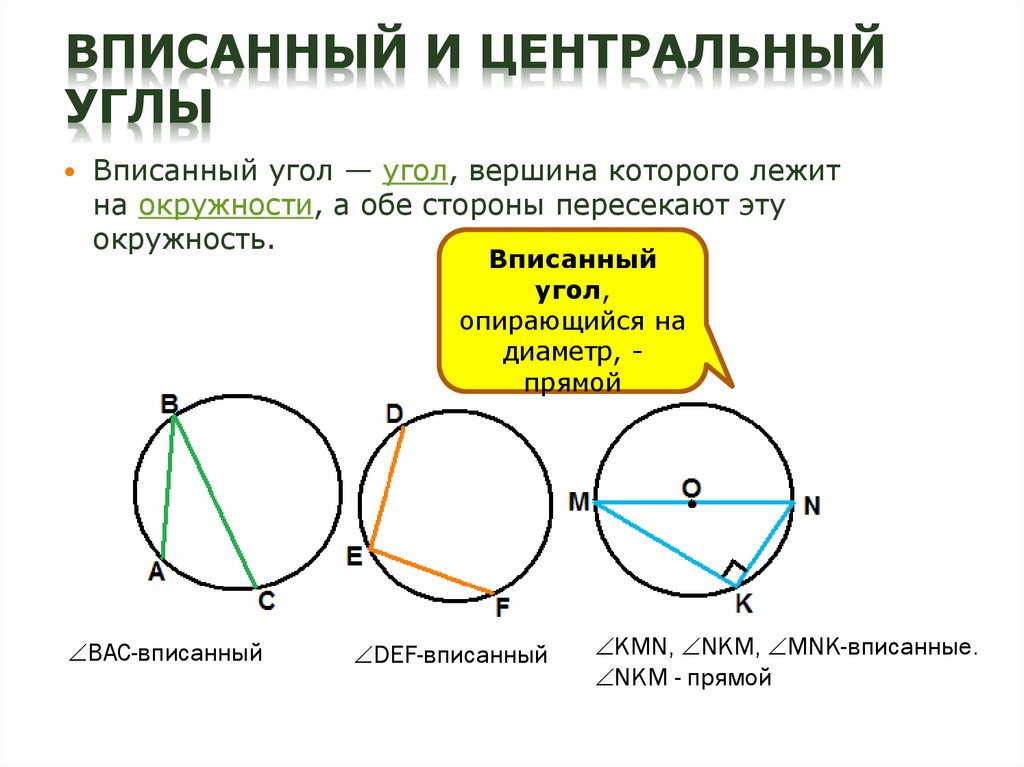
5. Вписанный и центральный углы

ВПИСАННЫЙ И ЦЕНТРАЛЬНЫЙ
УГЛЫ
Вписанный угол — угол, вершина которого лежит
на окружности, а обе стороны пересекают эту
окружность.
Вписанный
угол,
опирающийся на
диаметр, прямой
ВАС-вписанный
DEF-вписанный
KMN, NKM, MNK-вписанные.
NKM - прямой

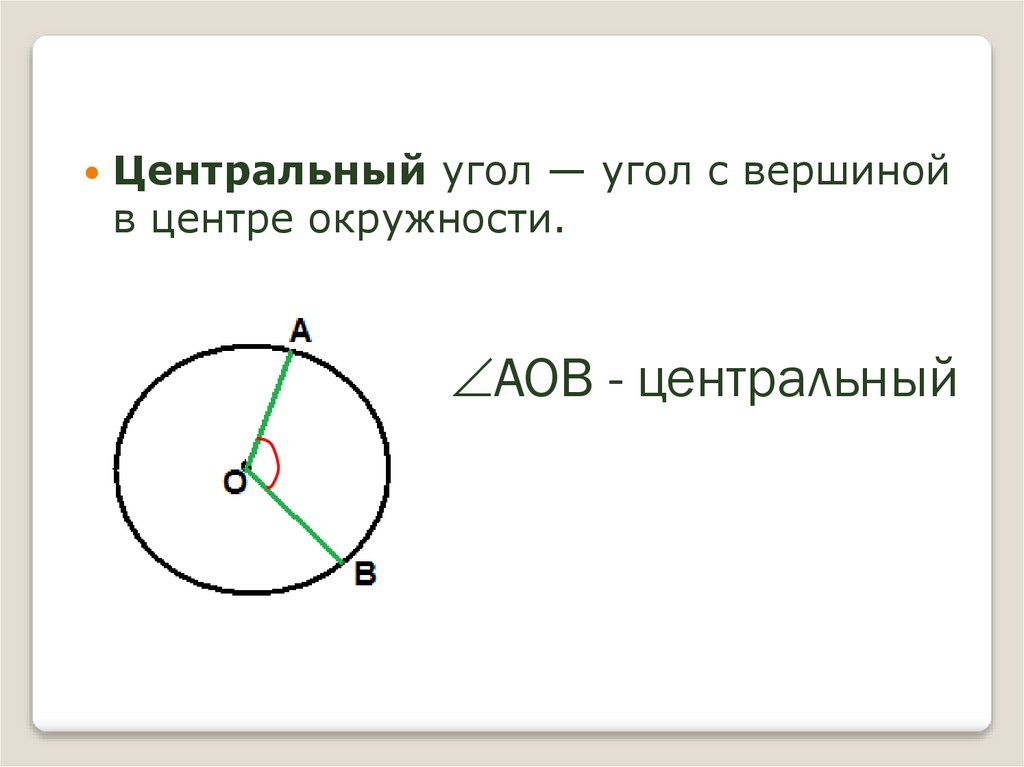
6.

Центральный угол — угол с вершиной
в центре окружности.
АОВ - центральный

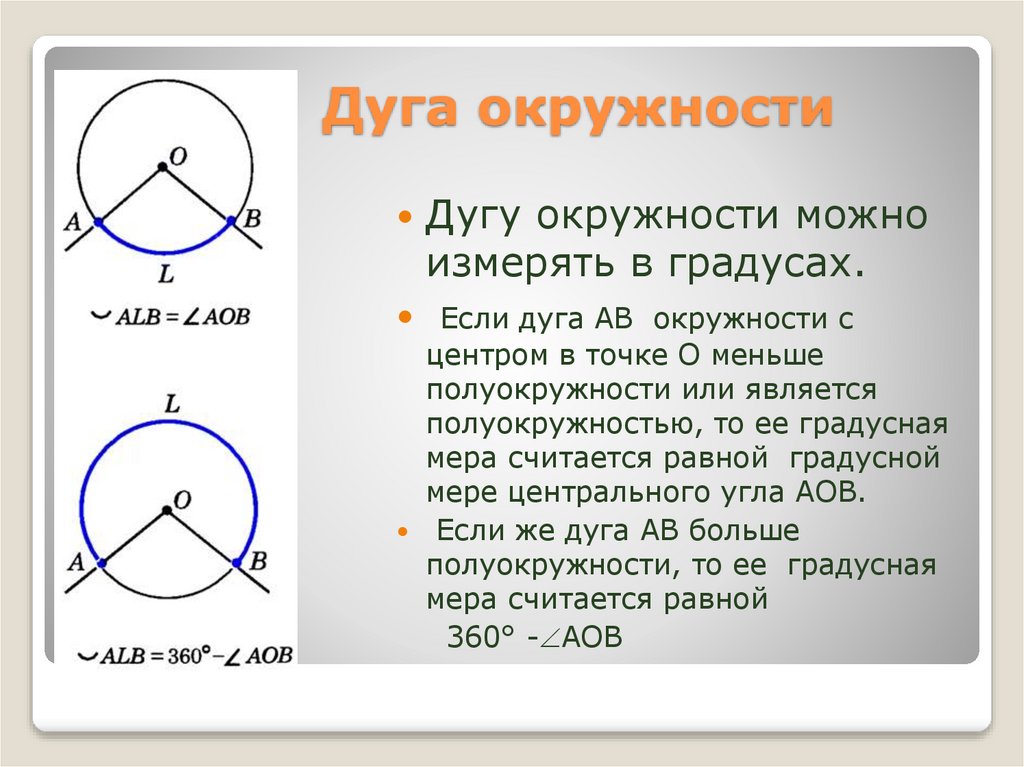
7. Дуга окружности

Дугу окружности можно
измерять в градусах.
Если дуга АВ окружности с
центром в точке О меньше
полуокружности или является
полуокружностью, то ее градусная
мера считается равной градусной
мере центрального угла АОВ.
Если же дуга АВ больше
полуокружности, то ее градусная
мера считается равной
360° - АОВ

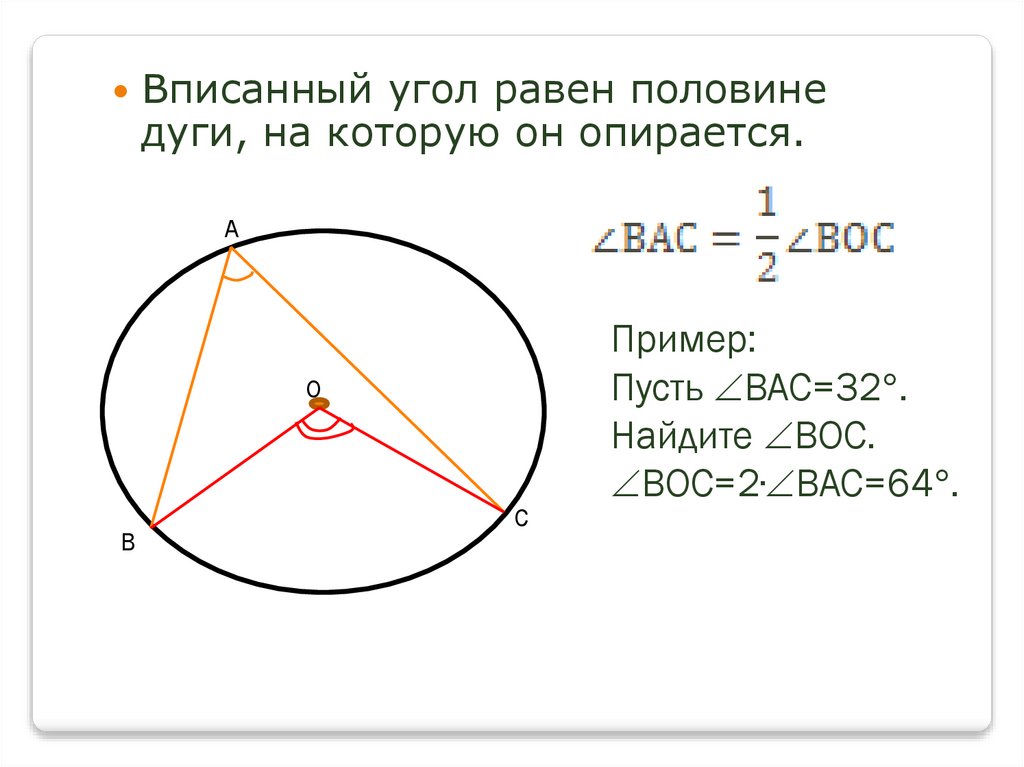
8.

Вписанный угол равен половине
дуги, на которую он опирается.
А
О
В
С
Пример:
Пусть ВАС=32 .
Найдите ВОС.
ВОС=2∙ ВАС=64 .

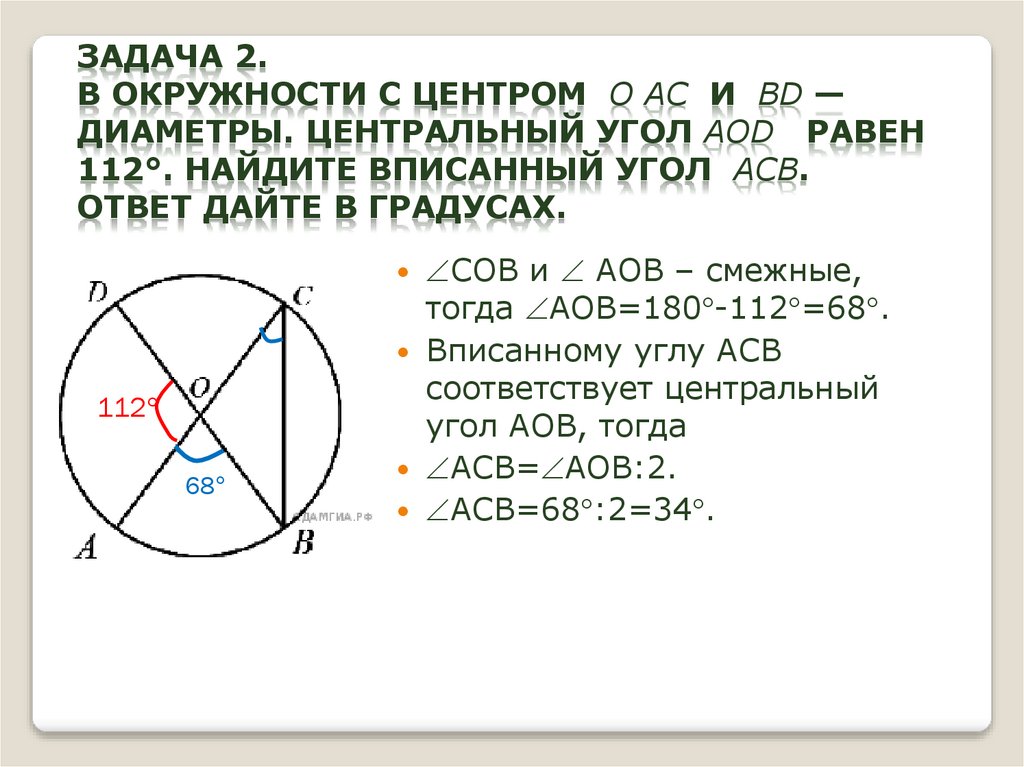
9. Задача 2. В окружности с центром  О АС  и  BD — диаметры. Центральный угол AOD   равен 112°. Найдите вписанный угол  ACB. Ответ

ЗАДАЧА 2.
В ОКРУЖНОСТИ С ЦЕНТРОМ О АС И BD —
ДИАМЕТРЫ. ЦЕНТРАЛЬНЫЙ УГОЛ AOD РАВЕН
112°. НАЙДИТЕ ВПИСАННЫЙ УГОЛ ACB.
ОТВЕТ ДАЙТЕ В ГРАДУСАХ.
СОВ и АОВ – смежные,
112
68
тогда АОВ=180 -112 =68 .
Вписанному углу АСВ
соответствует центральный
угол АОВ, тогда
АСВ= АОВ:2.
АСВ=68 :2=34 .

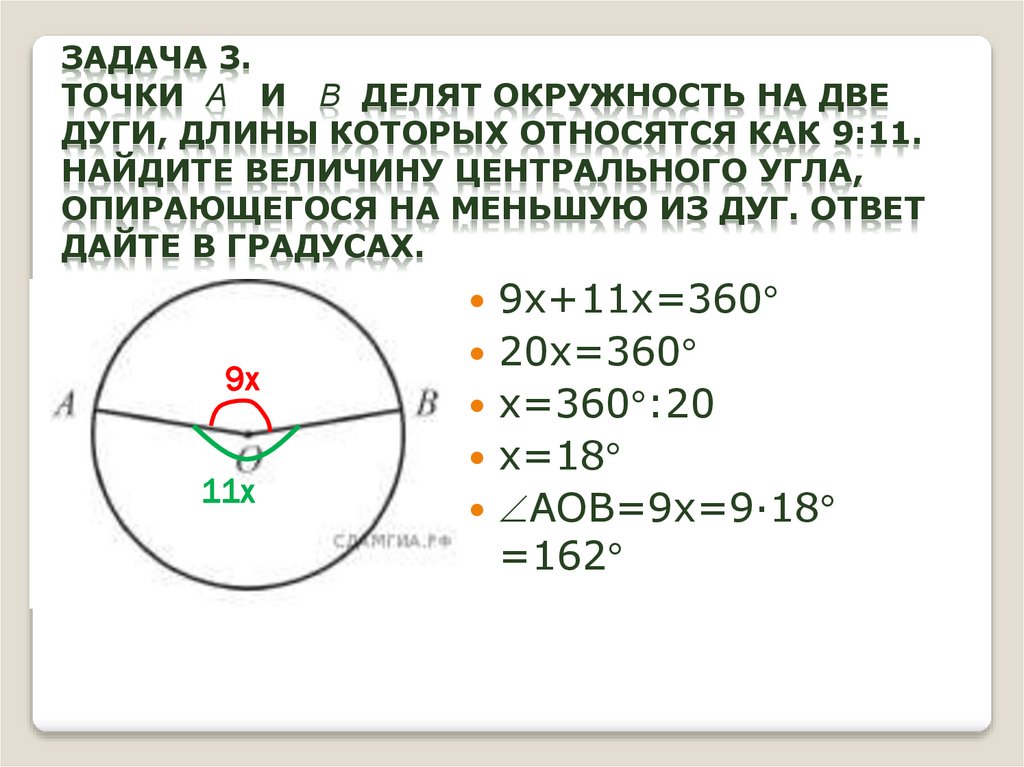
10. Задача 3. Точки  А   и   В  делят окружность на две дуги, длины которых относятся как 9:11. Найдите величину центрального угла,

ЗАДАЧА 3.
ТОЧКИ А И В ДЕЛЯТ ОКРУЖНОСТЬ НА ДВЕ
ДУГИ, ДЛИНЫ КОТОРЫХ ОТНОСЯТСЯ КАК 9:11.
НАЙДИТЕ ВЕЛИЧИНУ ЦЕНТРАЛЬНОГО УГЛА,
ОПИРАЮЩЕГОСЯ НА МЕНЬШУЮ ИЗ ДУГ. ОТВЕТ
ДАЙТЕ В ГРАДУСАХ.
9х+11х=360
9х
11х
20х=360
х=360 :20
х=18
АОВ=9х=9∙18
=162

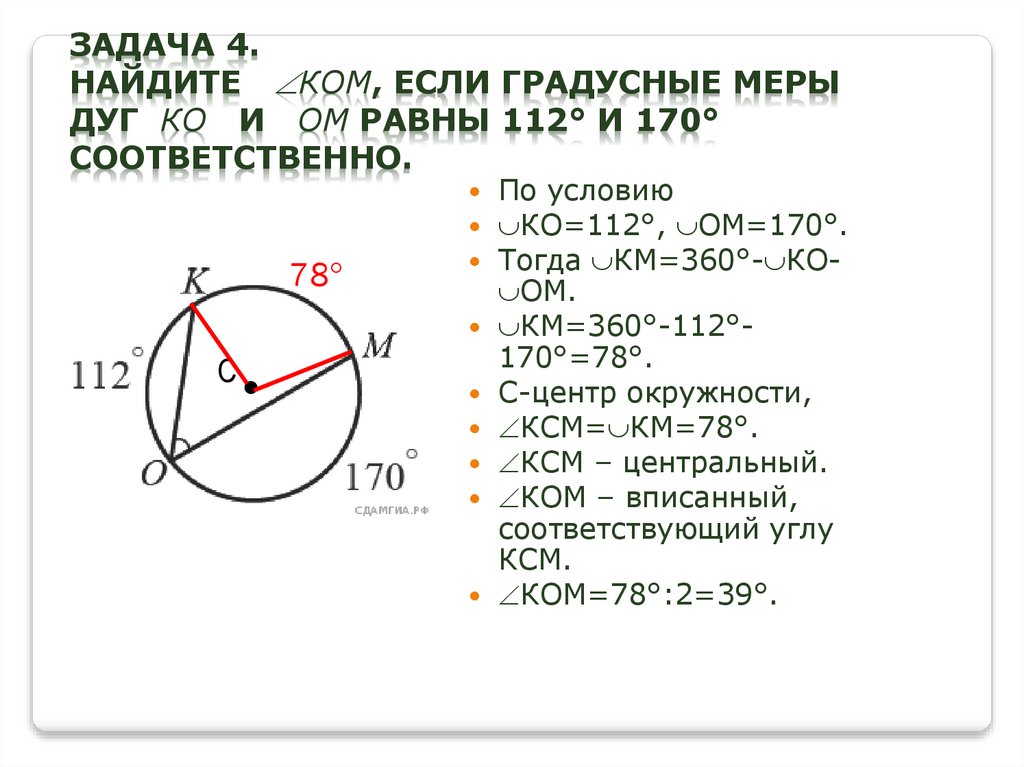
11. Задача 4. Найдите   КОМ, если градусные меры дуг  КО   и   ОМ равны 112° и 170° соответственно.

ЗАДАЧА 4.
НАЙДИТЕ КОМ, ЕСЛИ ГРАДУСНЫЕ МЕРЫ
ДУГ КО И ОМ РАВНЫ 112° И 170°
СООТВЕТСТВЕННО.
По условию
КО=112°, ОМ=170°.
Тогда КМ=360°- КО ОМ.
КМ=360°-112°170°=78°.
С-центр окружности,
КСМ= КМ=78°.
КСМ – центральный.
КОМ – вписанный,
соответствующий углу
КСМ.
КОМ=78°:2=39°.
78
С

12. Вписанные и описанные четырехугольники

ВПИСАННЫЕ И ОПИСАННЫЕ
ЧЕТЫРЕХУГОЛЬНИКИ
Свойство описанного
четырехугольника:
В любом описанном четырехугольнике
суммы противоположных сторон равны.
B
A
AD+BC=AB+CD
D
C

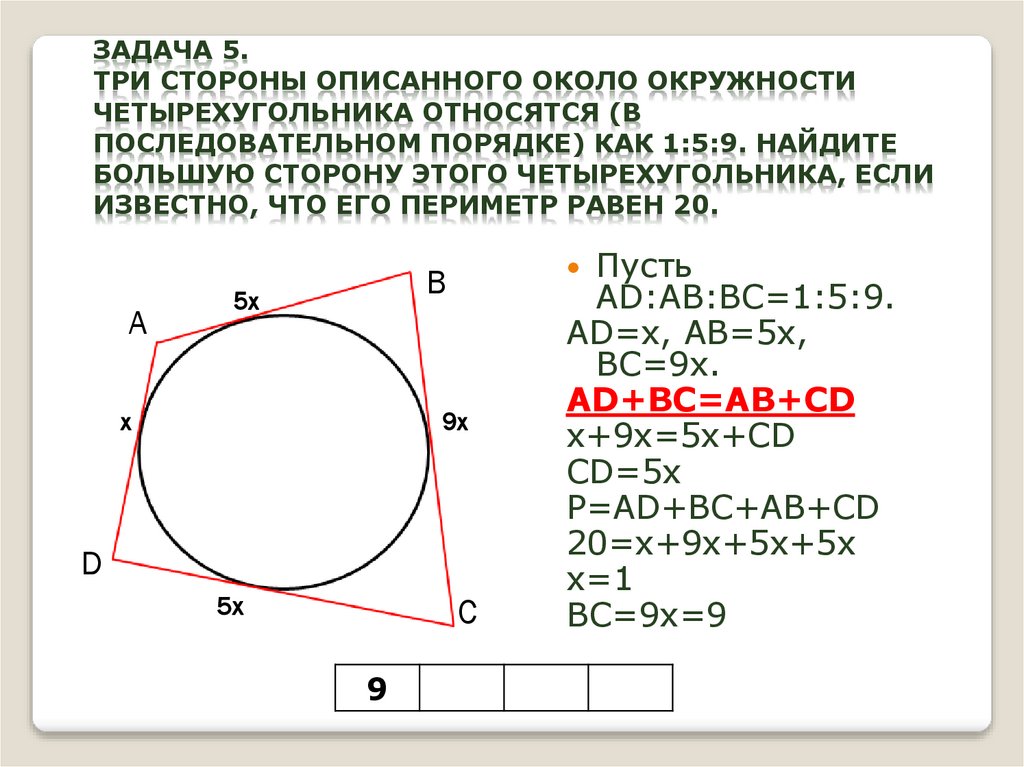
13. Задача 5. Три стороны описанного около окружности четырехугольника относятся (в последовательном порядке) как 1:5:9. Найдите

ЗАДАЧА 5.
ТРИ СТОРОНЫ ОПИСАННОГО ОКОЛО ОКРУЖНОСТИ
ЧЕТЫРЕХУГОЛЬНИКА ОТНОСЯТСЯ (В
ПОСЛЕДОВАТЕЛЬНОМ ПОРЯДКЕ) КАК 1:5:9. НАЙДИТЕ
БОЛЬШУЮ СТОРОНУ ЭТОГО ЧЕТЫРЕХУГОЛЬНИКА, ЕСЛИ
ИЗВЕСТНО, ЧТО ЕГО ПЕРИМЕТР РАВЕН 20.
A
Пусть
B
5x
x
9x
D
5x
C
9
AD:AB:BC=1:5:9.
AD=x, AB=5x,
BC=9x.
AD+BC=AB+CD
x+9x=5x+CD
CD=5x
P=AD+BC+AB+CD
20=x+9x+5x+5x
x=1
BC=9x=9

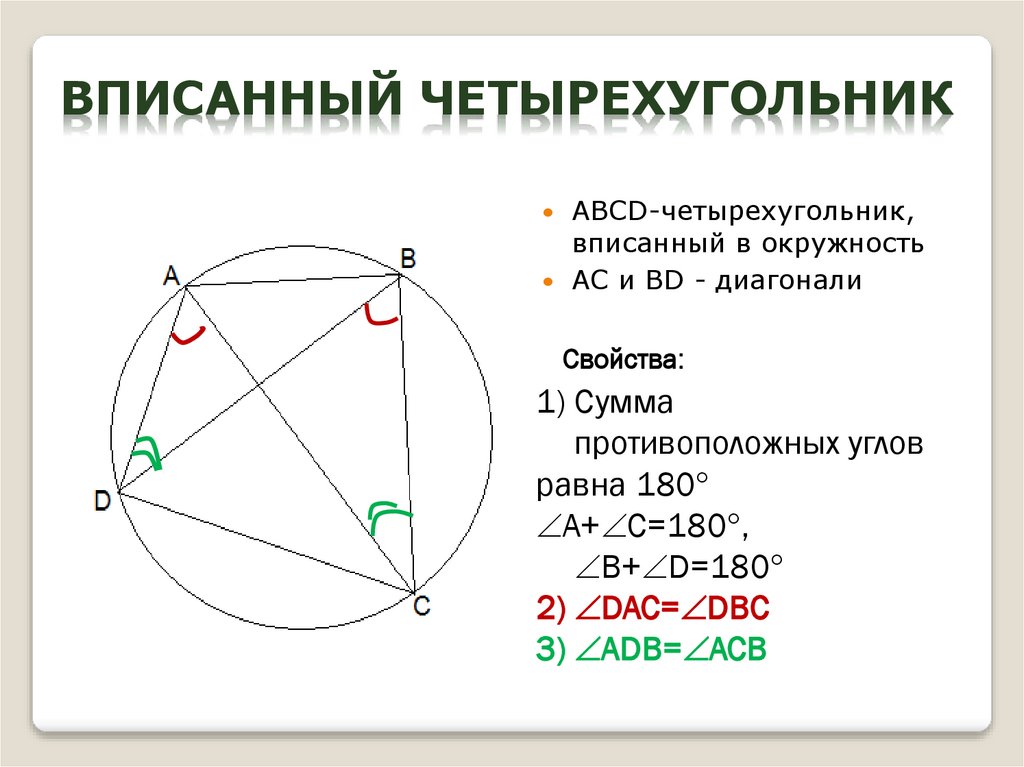
14. Вписанный четырехугольник

ВПИСАННЫЙ ЧЕТЫРЕХУГОЛЬНИК
ABCD-четырехугольник,
вписанный в окружность
АС и BD - диагонали
Свойства:
1) Сумма
противоположных углов
равна 180
A+ C=180 ,
B+ D=180
2) DAC= DBC
3) ADB= ACB

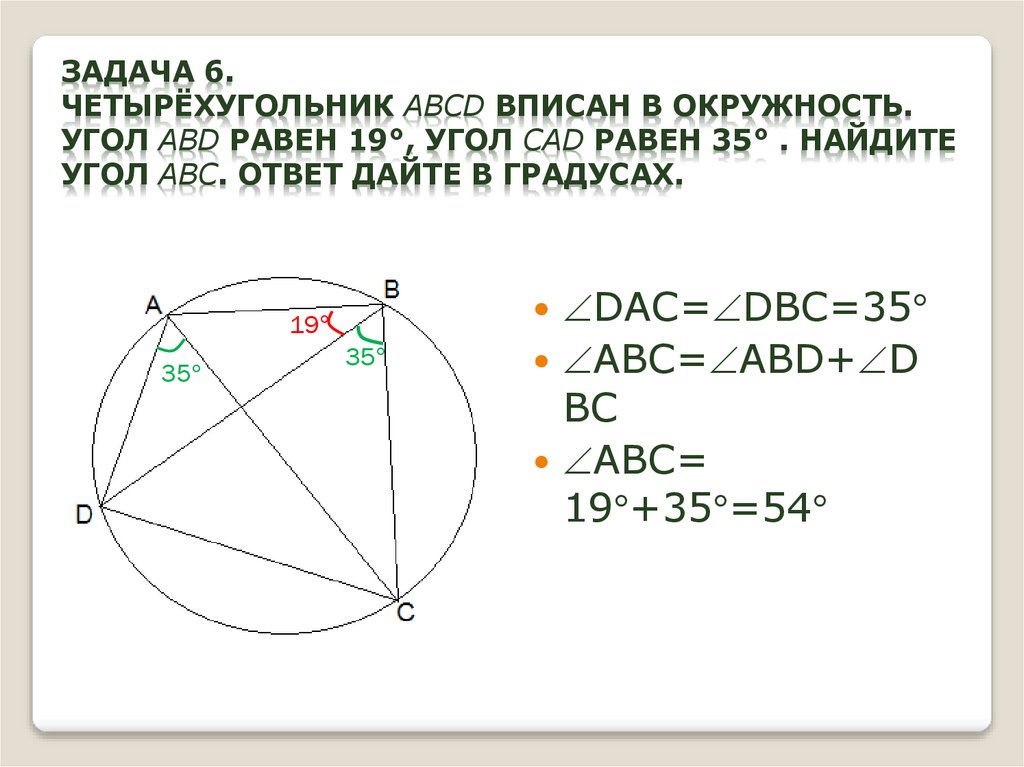
15. Задача 6. Четырёхугольник ABCD вписан в окружность. Угол ABD равен 19°, угол CAD равен 35° . Найдите угол ABC. Ответ дайте в

ЗАДАЧА 6.
ЧЕТЫРЁХУГОЛЬНИК ABCD ВПИСАН В ОКРУЖНОСТЬ.
УГОЛ ABD РАВЕН 19°, УГОЛ CAD РАВЕН 35° . НАЙДИТЕ
УГОЛ ABC. ОТВЕТ ДАЙТЕ В ГРАДУСАХ.
DAC= DBC=35
19
35
35
ABC= ABD+ D
BC
ABC=
19 +35 =54

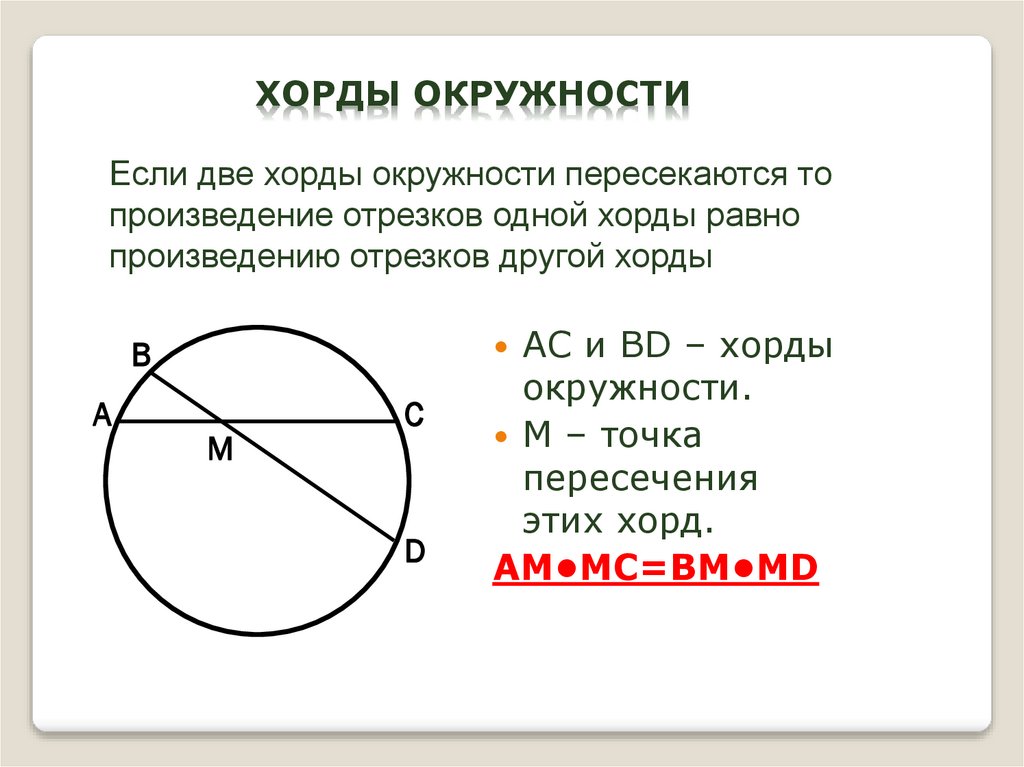
16. хорды окружности

ХОРДЫ ОКРУЖНОСТИ
Если две хорды окружности пересекаются то
произведение отрезков одной хорды равно
произведению отрезков другой хорды
AC и BD – хорды
B
A
M
C
D
окружности.
М – точка
пересечения
этих хорд.
AM•MC=BM•MD

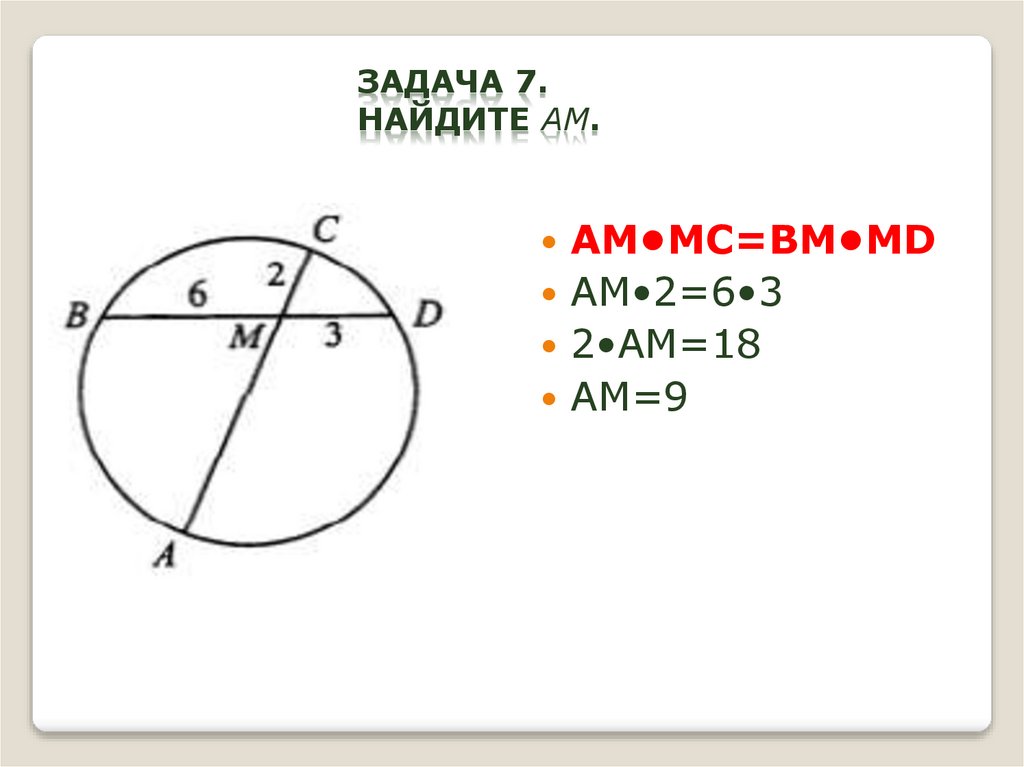
17. Задача 7. Найдите АМ.

ЗАДАЧА 7.
НАЙДИТЕ АМ.
AM•MC=BM•MD
AM•2=6•3
2•AM=18
AM=9