Оригами в помощь геометрии

1. Оригами в помощь геометрии

Выполнили: ученики 8 класса.
ГУО «Хуторская ясли-сад-средняя школа»
Алепинов Василий Евланов Николай
Руководитель: Воробей В.В

2.

Гипотеза: искусство
оригами
имеет прямое отношение к
геометрии.
Цель исследования - применение
оригами в процессе освоения
геометрического материала ,
решении задач, доказательстве
теорем.

3.

Новизна нашей работы
применение оригинальных
идей решения задач с
помощью листа бумаги

4. Для достижения цели и проверки гипотезы нами были решены следующие задачи:

1.Расширить кругозор знаний по
математике, знакомясь с искусством
оригами и соответствующей литературой.
2.Рассмотреть решение задач и
доказательство теорем с помощью
оригами.
3.Подобрать материал по использованию
оригами на уроках математики, геометрии.
4.Установить связь между математикой и
оригами.
5.Сделать выводы о проделанной работе.

5.

математическая
обработка
данных;
Методы
обобщение
исследова
ния
Источниковедческий анализ
литературы
практическая
деятельность по
овладению
оригамским
методом
решения задач

6. Оригами в помощь геометрии

ОБЪЕКТ
ИССЛЕДОВАНИЯ
Оригами
ПРЕДМЕТ
ИССЛЕДОВАНИЯ
Математика

7.

Практическую значимость
исследовательской работы
видим:
в определении роли
оригами в процессе
изучения геометрии

8. Почему мы заинтересовались оригами?

В детстве нам нравилось складывать самолетики,
различные фигурки, коробочки и т.д.
Нам стало интересно, насколько близко связано
искусство оригами с математикой?

9.

Слово Оригами в переводе с японского означает
«сложенный из бумаги». В японском языке его
пишут с помощью двух иероглифов:
ОРИ БУМАГА
КАМИСЛОЖЕННЫЙ
История возникновения ОРИГАМИ неразрывно
связана с изобретением бумаги.

10. История оригами

Оригами - это
самобытное японское
искусство создания
моделей различных
предметов, животных,
птиц, цветов путем
сгибания листа бумаги.

11.

12.

13. В оригаметрии считается:

Роль прямых будут играть края
листа и линии сгибов,
образующиеся при его
перегибании.
Роль точек – вершины углов листа
и точки пересечения линий
сгибов друг с другом или с
краями листов.

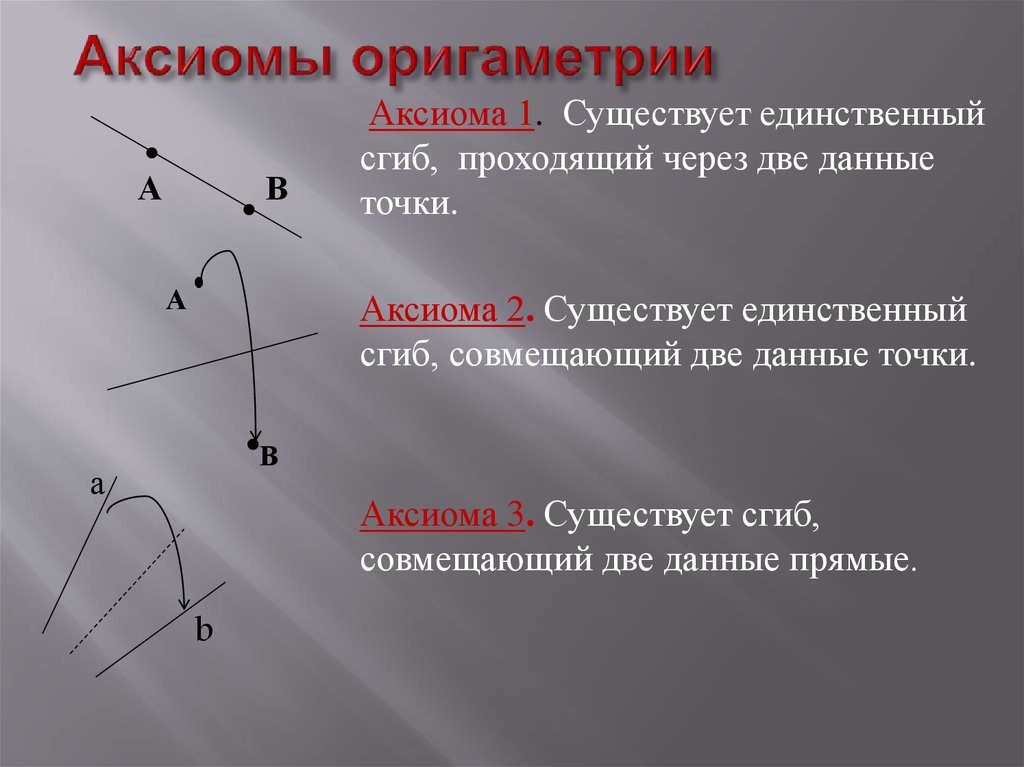
14. Аксиомы оригаметрии

А
В
А
Аксиома 1. Существует единственный
сгиб, проходящий через две данные
точки.
Аксиома 2. Существует единственный
сгиб, совмещающий две данные точки.
В
а
Аксиома 3. Существует сгиб,
совмещающий две данные прямые.
b

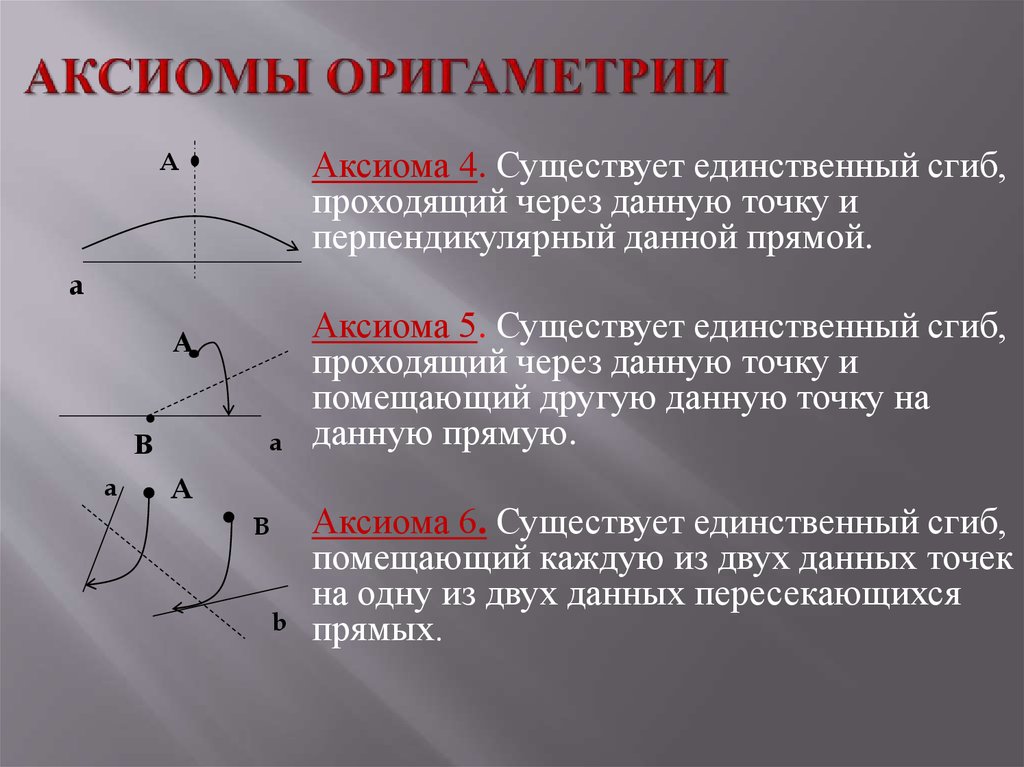
15. Аксиомы оригаметрии

Аксиома 4. Существует единственный сгиб,
проходящий через данную точку и
перпендикулярный данной прямой.
A
a
А
a
В
a
A
B
b
Аксиома 5. Существует единственный сгиб,
проходящий через данную точку и
помещающий другую данную точку на
данную прямую.
Аксиома 6. Существует единственный сгиб,
помещающий каждую из двух данных точек
на одну из двух данных пересекающихся
прямых.

16.

В 2002 году японский оригамист Коширо Хатори
обнаружил сгиб,который описал в аксиоме
Хумиани Хузита
Аксиома 7. Для двух данных прямых и точки
существует линия сгиба, перпендикулярная первой
прямой и помещающая данную точку на вторую
прямую .

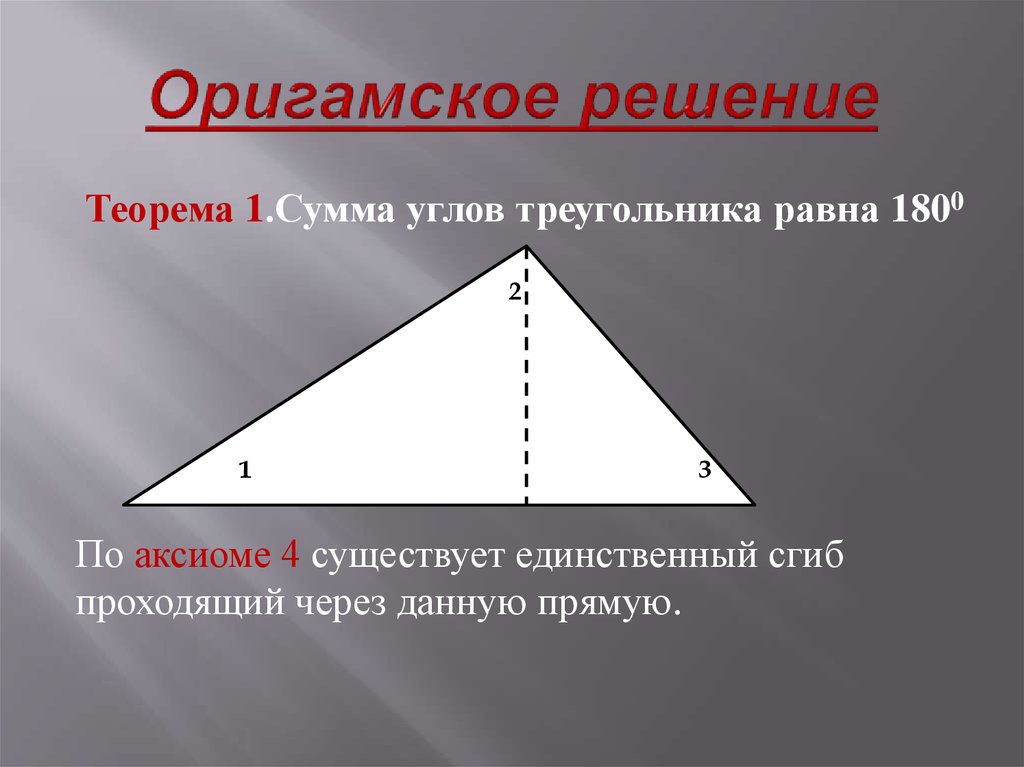
17. Оригамское решение

Теорема 1.Сумма углов треугольника равна 1800
2
1
3
По аксиоме 4 существует единственный сгиб
проходящий через данную прямую.

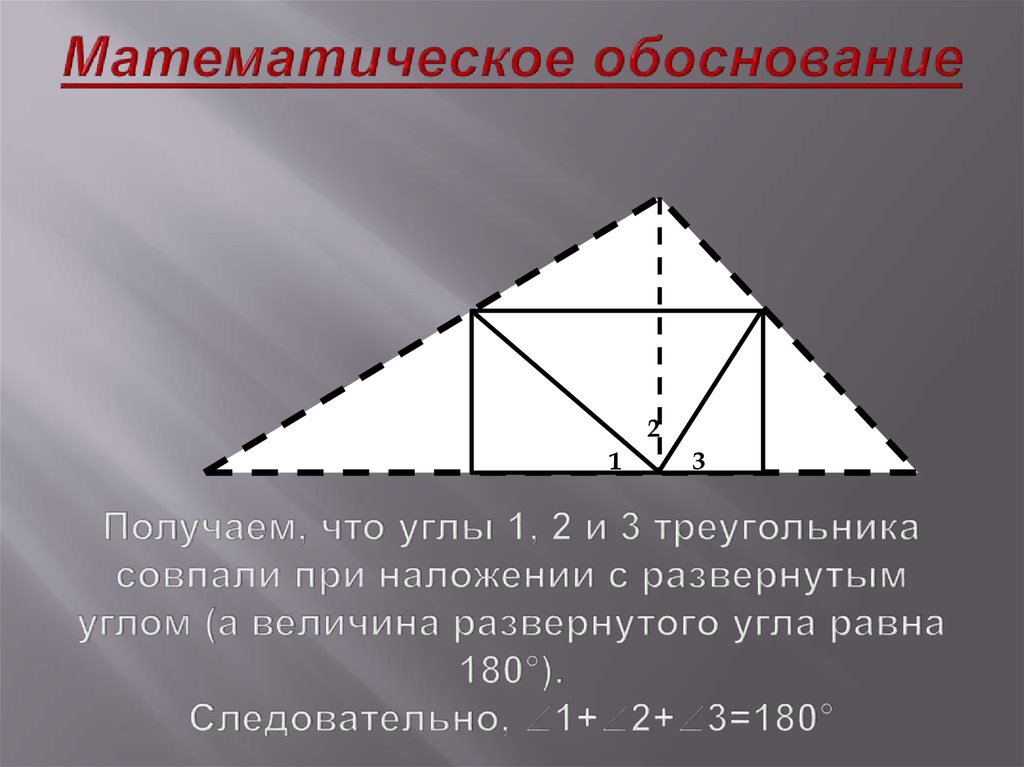
18. Математическое обоснование Получаем, что углы 1, 2 и 3 треугольника совпали при наложении с развернутым углом (а величина развернутого угла

2
1
3

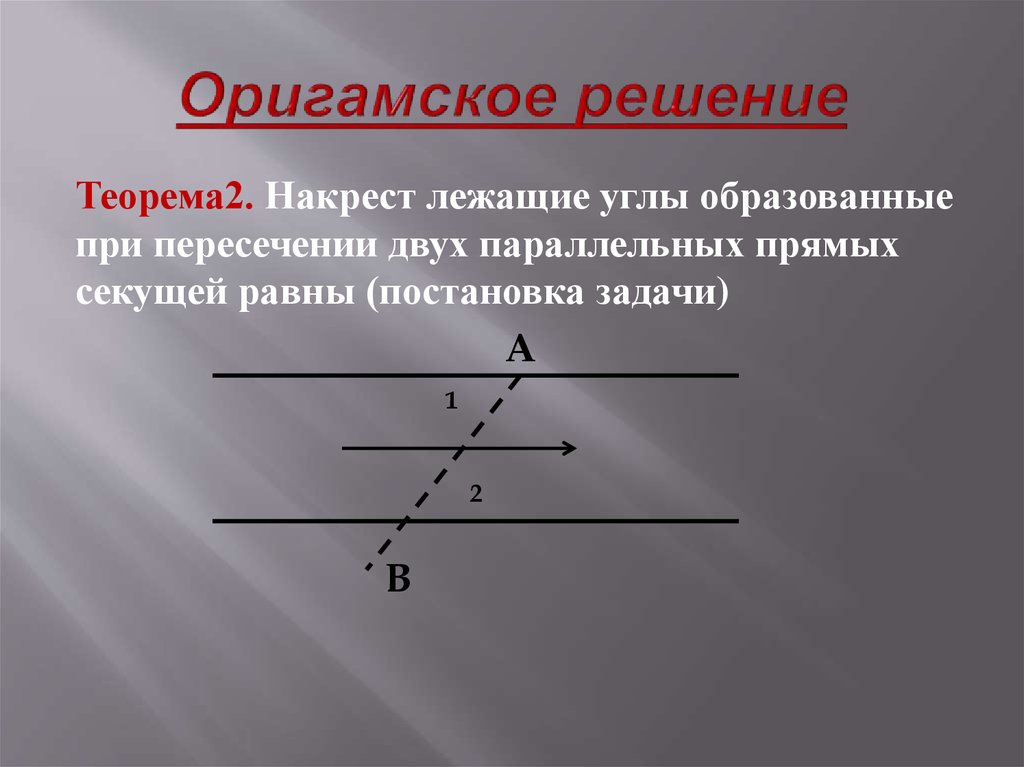
19. Оригамское решение

Теорема2. Накрест лежащие углы образованные
при пересечении двух параллельных прямых
секущей равны (постановка задачи)
A
1
2
B

20.

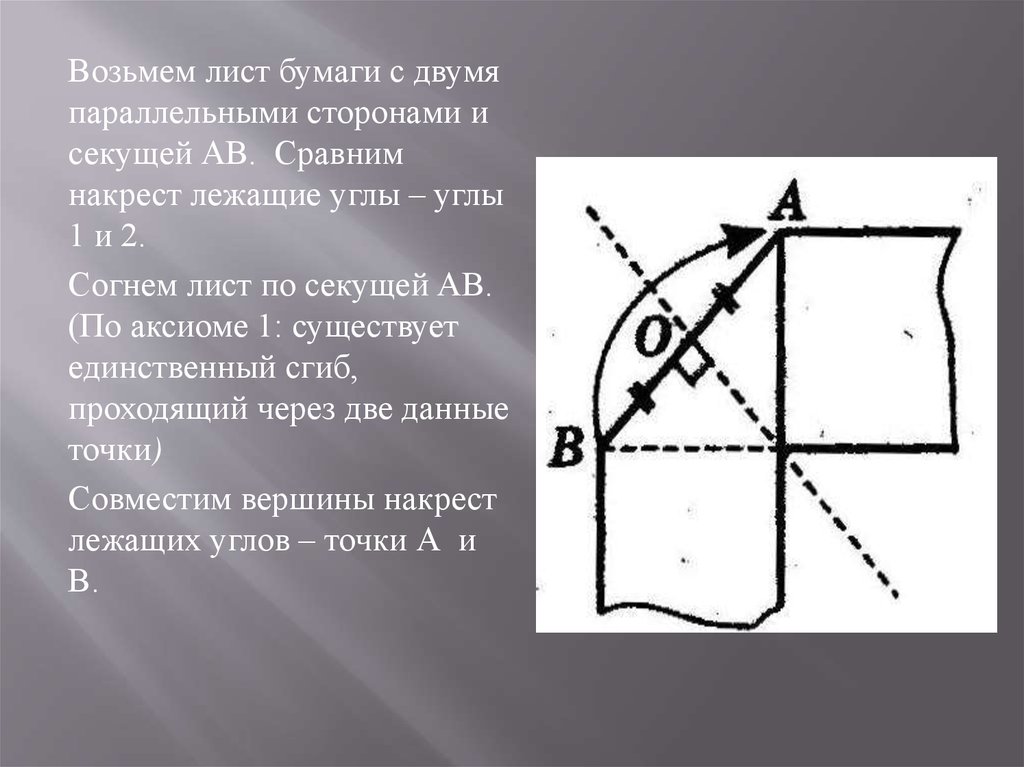
Возьмем лист бумаги с двумя
параллельными сторонами и
секущей АВ. Сравним
накрест лежащие углы – углы
1 и 2.
Согнем лист по секущей АВ.
(По аксиоме 1: существует
единственный сгиб,
проходящий через две данные
точки)
Совместим вершины накрест
лежащих углов – точки А и
В.

21. 3) Математическое обоснование   А(В) 1=2 О Математическое обоснование       Углы 1 и 2 совпали при наложении, следовательно, 1=2 (два угла назы

22. Из чего состоит любая оригамская задача ?

Из постановки задачи
Из оригамского решения ,проверки
или способа построения
Из математического обоснования, то
есть доказательства того, что в
результате действительно получается
фигура с требуемыми свойствами

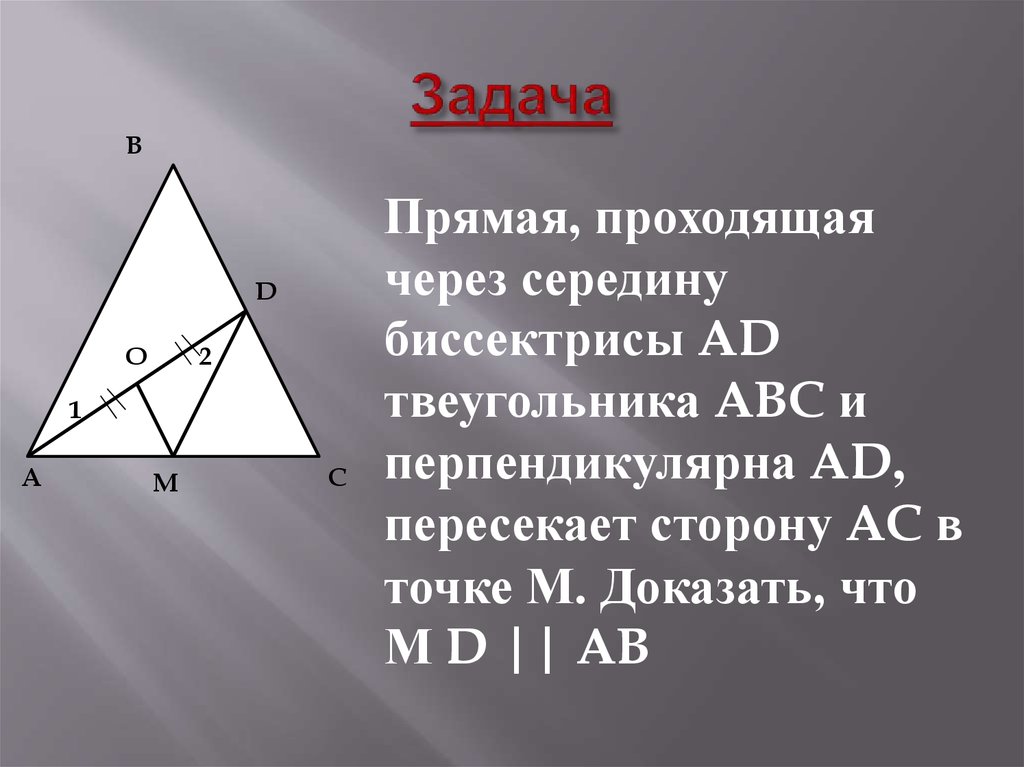
23. Задача

B
D
O
2
1
A
M
C
Прямая, проходящая
через середину
биссектрисы AD
твеугольника ABC и
перпендикулярна AD,
пересекает сторону AC в
точке М. Доказать, что
М D || AB

24.

B
D
C
A
B
D
O
A
M
C
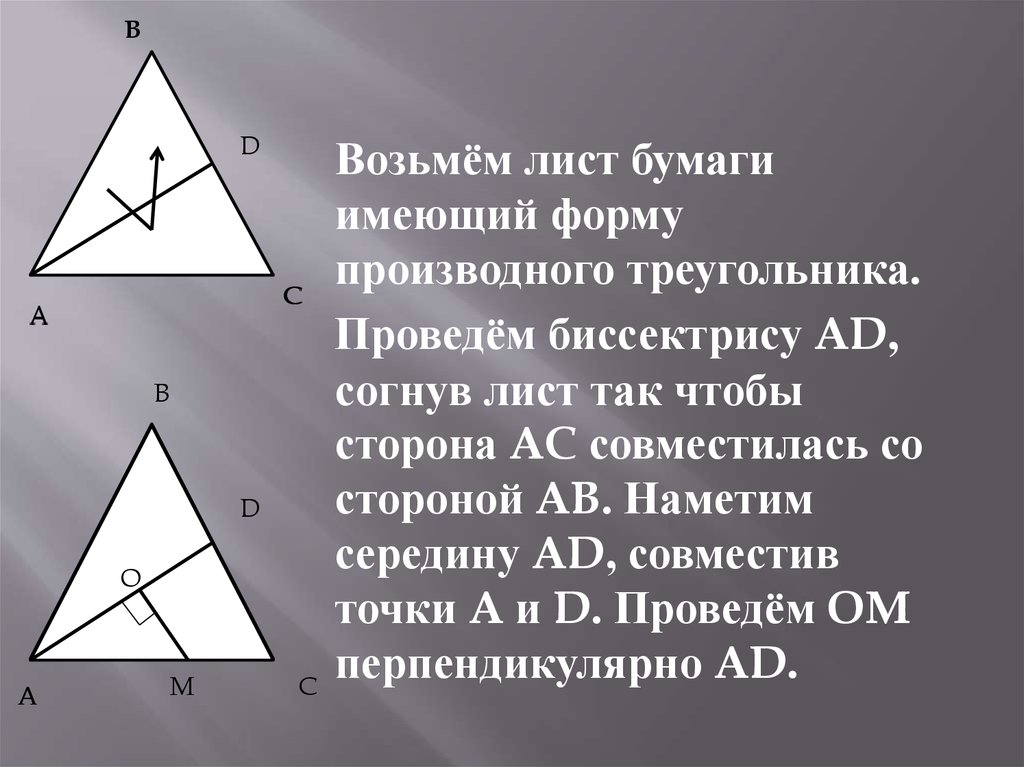
Возьмём лист бумаги
имеющий форму
производного треугольника.
Проведём биссектрису AD,
согнув лист так чтобы
сторона AC совместилась со
стороной AB. Наметим
середину AD, совместив
точки A и D. Проведём OM
перпендикулярно AD.

25.

B
D
O
2
1
A
M
C
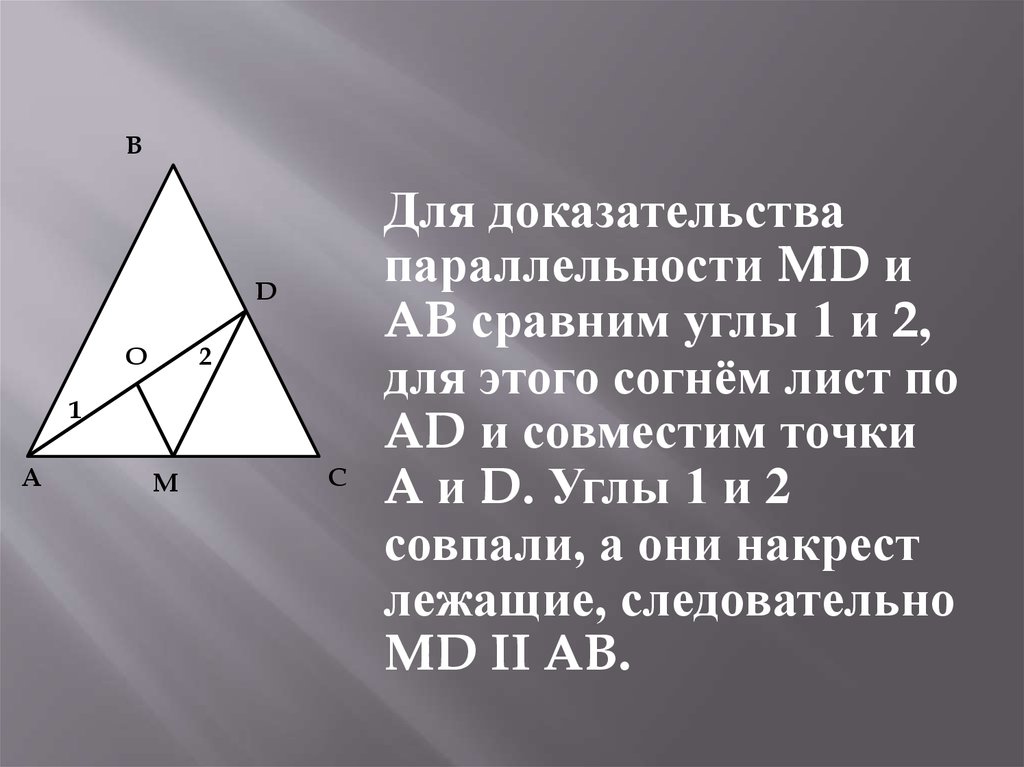
Для доказательства
параллельности MD и
AB сравним углы 1 и 2,
для этого согнём лист по
AD и совместим точки
A и D. Углы 1 и 2
совпали, а они накрест
лежащие, следовательно
MD II AB.

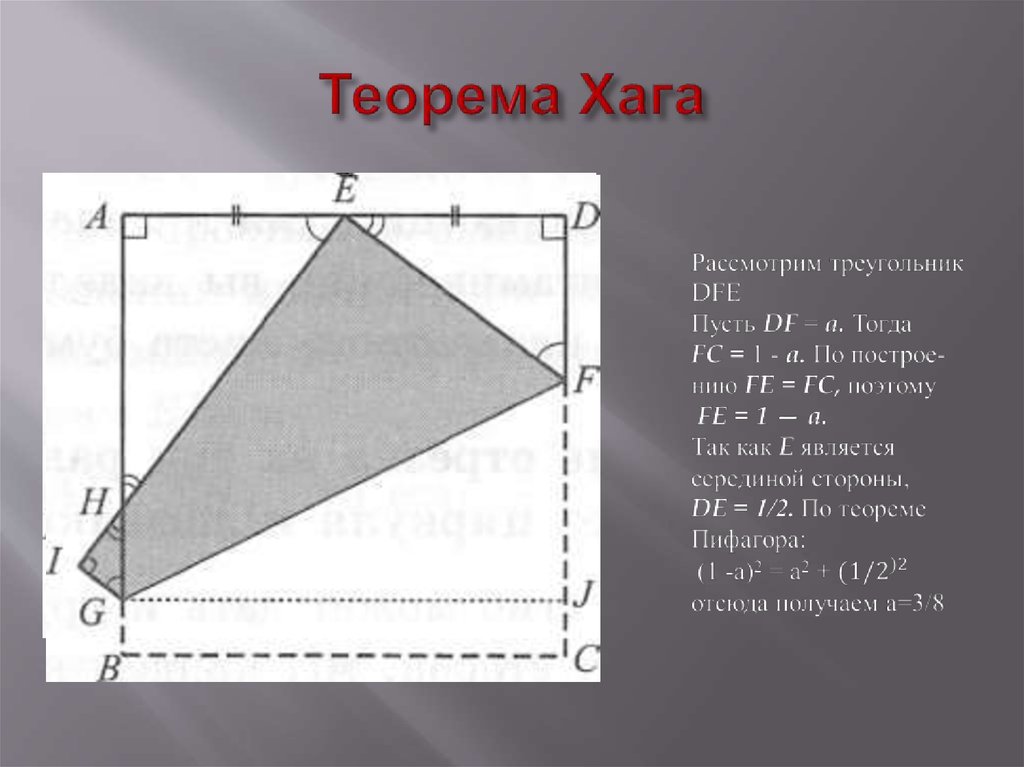
26. Теорема Хага

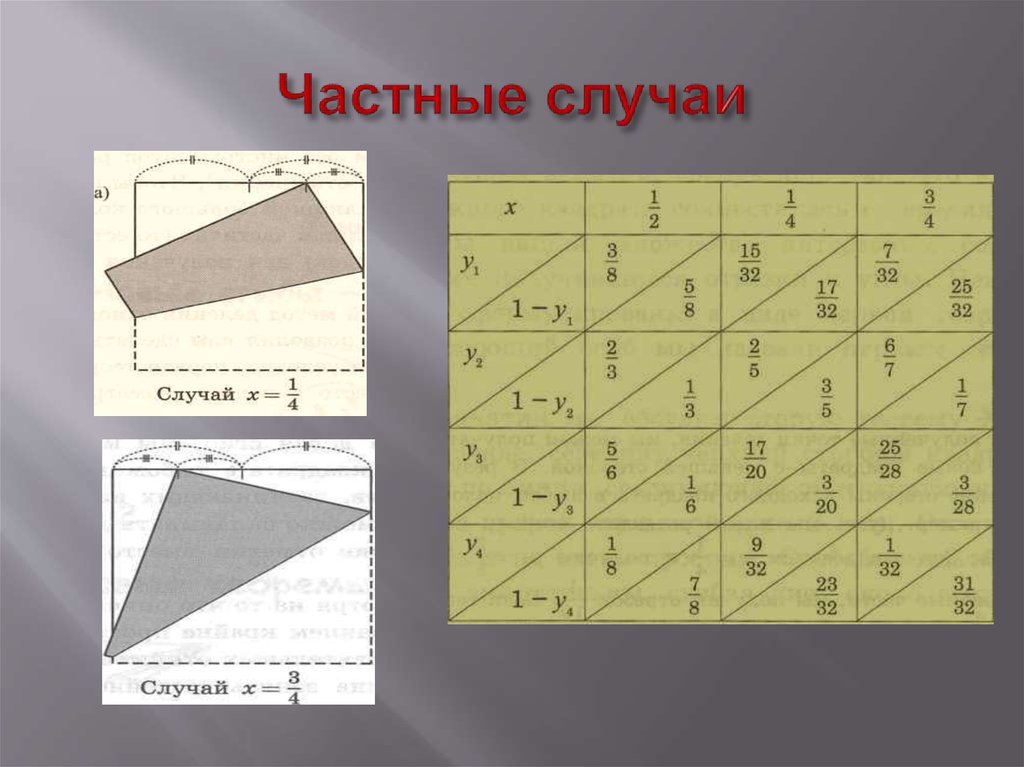
27. Обобщение теоремы

1
1
F
H
G
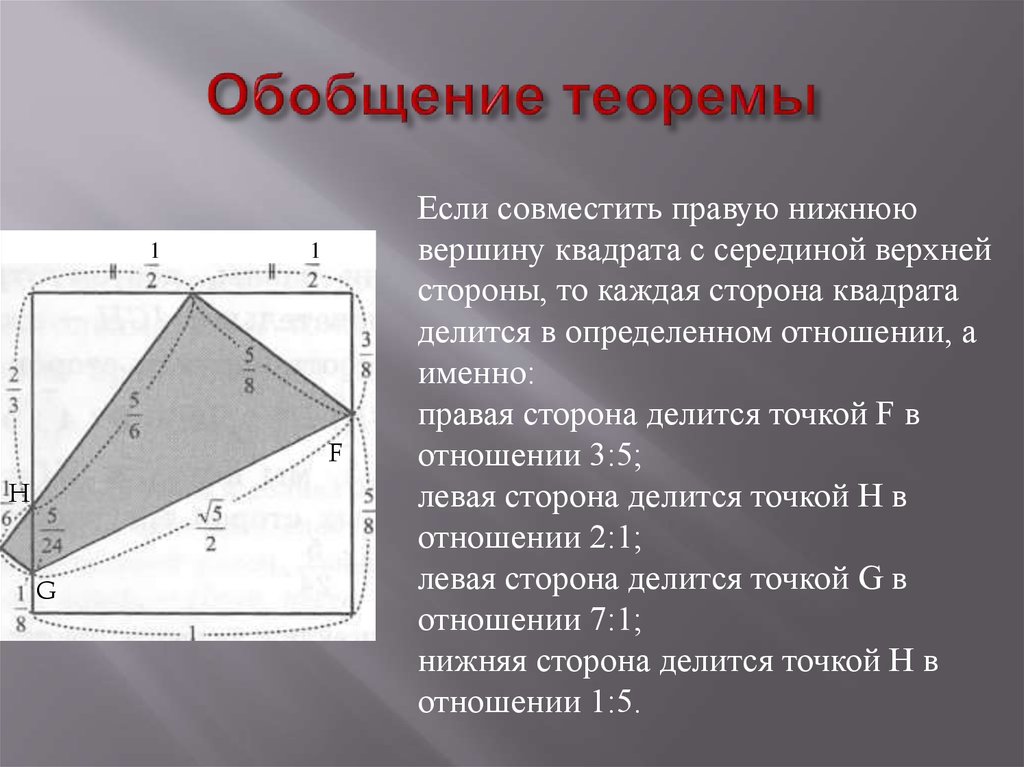
Если совместить правую нижнюю
вершину квадрата с серединой верхней
стороны, то каждая сторона квадрата
делится в определенном отношении, а
именно:
правая сторона делится точкой F в
отношении 3:5;
левая сторона делится точкой Н в
отношении 2:1;
левая сторона делится точкой G в
отношении 7:1;
нижняя сторона делится точкой Н в
отношении 1:5.

28. Частные случаи

29. Деление квадрата на три равные части

Согнем бумагу так, чтобы правая
нижняя вершина лежала на левой
стороне листа, затем двигаем эту
вершину вдоль левой стороны до
тех пор, пока правый край листа не
пройдет через середину верхней
стороны. Сделаем складку. Левая
сторона квадрата делится на две
части, меньшая из которых
составляет треть от всей стороны.

30.

Центральное место геометрии треугольника
занимают свойства так называемых
замечательных точек и линий. Более подробно
рассмотрим использование оригами для
построения точки пересечения медиан. На
треугольном листе бумаги путём совмещения
двух вершин углов устанавливаем засечку –
таким образом определяем середину стороны.
На следующем этапе проводим линию сгиба
через вершину угла и намеченную середину
противолежащей стороны эта линия сгиба
является медианой треугольника. Можно ли
ещё провести линии сгибов, являющейся
медианами треугольника? Учитывая
определение и реализуя выше описанную
последовательность выполненной работы
построим ещё две медианы. Они пересекаются
в одной точке, являющейся центром тяжести
(центроидом) треугольника.

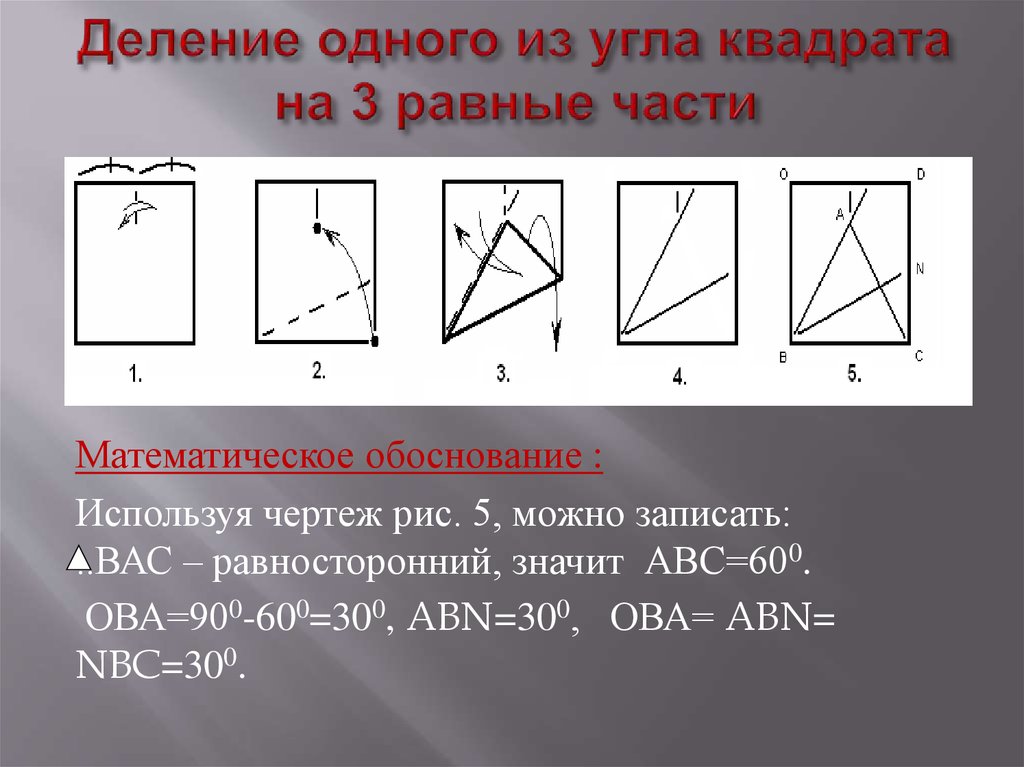
31. Деление одного из угла квадрата на 3 равные части

Математическое обоснование :
Используя чертеж рис. 5, можно записать:
..ВАС – равносторонний, значит АВС=600.
ОВА=900-600=300, ABN=300, ОВА= ABN=
NBC=300.

32.

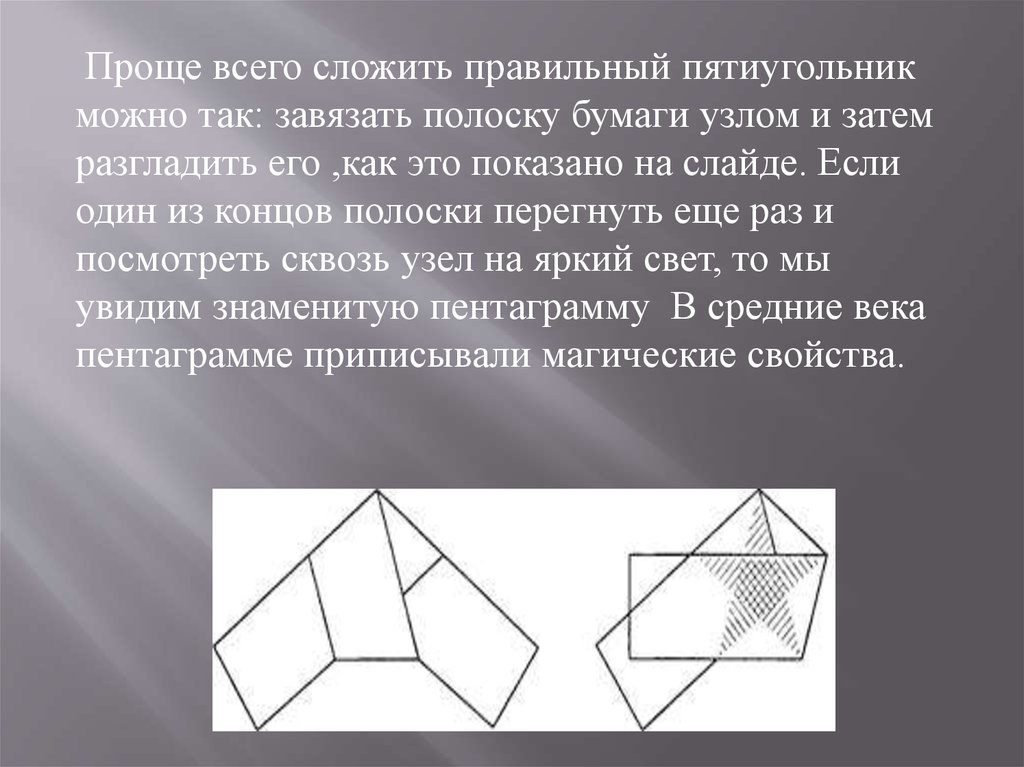
Проще всего сложить правильный пятиугольник
можно так: завязать полоску бумаги узлом и затем
разгладить его ,как это показано на слайде. Если
один из концов полоски перегнуть еще раз и
посмотреть сквозь узел на яркий свет, то мы
увидим знаменитую пентаграмму В средние века
пентаграмме приписывали магические свойства.

33. Построение параболы, путем построения семейства касательных

Перегибая лист бумаги можно легко построить параболу. Отступив от
края листа, поставим на нем точку.Перегибая лист (нам понадобится
сделать около 20 перегибаний), будем следить за тем, чтобы каждый раз
край листа проходил через поставленную нами точку. На слайде хорошо
видна возникающая при этом полная иллюзия начерченной параболы.
Отмеченная точка служит фокусом параболы, край листа — ее
директрисой, а линия сгиба—касательной к параболе. Нетрудно видеть,
что по самому построению любая точка кривой равноудалена от фокуса
и директрисы. Именно это свойство и определяет параболу.

34.

35.

36.

37.

Спасибо за
внимание !