Множества и операции над ними. Дискретная математика

1.

Дискретная математика
Лекция 1.
Множества и операции
над ними
Преподаватель к.пед.наук,
доцент кафедры ЕНДиИТ
Герасимова О.Ю.

2.

Содержание лекции
1.Понятие множества
2.Способы задания множеств
3.Основные определения
4.Диаграмма Эйлера – Венна
5.Операции над множествами
6. Системы множеств
7.Законы алгебры множеств
8.Решение типовых задач по теме «Теория множеств»
9.Вопросы и упражнения
10.Задачи

3.

Введение
Дискретная
математика
–
направление
в
математике,
объединяющее
отдельные
её
разделы, ранее сформированные как
самостоятельные теории. К ним
относятся математическая логика и
теории
множеств,
графов,
кодирования, автоматов.

4.

Введение
• Дискретной математикой называют
совокупность математических
дисциплин, изучающих свойства
математических моделей объектов,
процессов, зависимостей,
существующих в реальном мире,
которыми оперируют в различных
областях знаний.

5.

Введение
Георг Кантор (G.Cantor, 1845-1918) –
немецкий математик, основатель теории
множеств, писал:
«Под многообразием или множеством я
понимаю вообще все многое, которое
возможно мыслить как единое, т.е. такую
совокупность определенных элементов,
которая посредством одного закона
может быть соединена в одно целое».

6.

1. Понятие множества
Теория множеств опирается на три первичных
понятия:
1) множество;
2) элемент;
3) принадлежность.
Строгого определения этим понятиям не
дается, описывается только их применение. Для
этих понятий используются обозначения:
a А элемент а принадлежит множеству А;
a А
элемент а не принадлежит множеству А.

7.

1. Понятие множества
Совокупность элементов,
объединённых некоторым признаком,
свойством, составляет понятие
множество. Например, множество книг в
библиотеке, множество студентов в
группе, множество натуральных чисел N
и т.д.

8.

1. Понятие множества
Говоря о некотором множестве, мы
требуем его:
целостности, т.е. возможности
рассматривать его как отдельный
объект;
различимости его элементов;
неупорядоченности элементов.
Поэтому записи {a, b} и {b, a} определяют
одно и то же множество!

9.

2. Способы задания множеств
• Множество можно задать, перечислив все
его элементы: A = {a, b, c}, B = {-1,3,6,8,…}.
Порядок записи элементов множества
произволен.

10.

2. Способы задания множеств
При рекурсивном задании множество
задается перечисляющей процедурой
(алгоритмом).
Пример. Множество натуральных чисел N
задаем следующими правилами:
• Задаем исходный элемент: 1 ∈ N,
• Задаем алгоритм: n ∈ N ⇒ (n+1) ∈ N

11.

2. Способы задания множеств
Наиболее общий способ задания множеств указывается его характеристическое
свойство, которое для каждого элемента
позволяет выяснить, принадлежит он
множеству или нет.
Например,
• B = { x│x – целый корень уравнения 2x3 - x2 +
1 = 0},
• C = {x - 1 ≤x ≥7, x – целое }.

12.

2. Способы задания множеств
В
дальнейшем
для известных числовых
множеств будут использоваться обозначения:
N = { 1,2,3,…} – множество натуральных чисел;
Z = { …, -2,-1,0,1,2,…} – множество целых
чисел;
Q – множество рациональных чисел;
R – множество действительных чисел;
C — множество комплексных чисел.

13.

3. Основные определения
• Определение 1. Пустым множеством
называется множество, не содержащее ни
одного элемента. Обозначение: Ø.
• Определение 2. Два множества A и В
называются равными, если они состоят из
одних и тех же элементов.
• Обозначение: A=B.

14.

3. Основные определения
• Определение 3. Множество B называется
подмножеством или частью множества A,
если каждый элемент множества B является
элементом множества A.
• Обозначение: B ⊆ A (нестрогое включение).

15.

3. Основные определения
• Из определения 3 следует, что два
множества A и В называются равными, если
А ⊆ В и B ⊆ A. Таким образом, чтобы
доказать равенство множеств, требуется
установить два включения.
• Если B ≠ Ø, B ⊆ A и B ≠ A, то говорят, что B
есть собственное подмножество A.
• Обозначение: B ⊂ A (строгое включение).

16.

3. Основные определения
• Определение 4. Множество всех
подмножеств множества А называется
множеством-степенью или булеаном
множества А.
• Обозначение: 2А или P(А).
Таким образом,
2А ={Х: Х ⊆ А} или P(А) ={Х: Х ⊆ А}.
где А – это мощность множества

17.

3. Основные определения
• Пример .
Пусть B = {1,2,3}.
Тогда его булеан
Р(B)={{1,2,3},{1,2}, {2,3}, {3,1}, {1}, {2}, {3},Ø }.

18.

3. Основные определения
Универсальным называется множество,
состоящее из всех возможных элементов,
рассматриваемых в данной задаче.
Обозначение: I или U.
Универсальное
множество
удобно
изображать графически в виде множества
точек прямоугольника.

19.

3. Основные определения
Примеры
1) Пусть U = Z и требуется найти все решения
уравнения x2=2
Множество М решений этой задачи есть пустое
множество: М = .
2) Пусть теперь U = R. Тогда множество М
решений уравнения x2=2
Не пусто: М = {− 2, 2} .

20.

3. Основные определения
Упорядоченные множества или кортежи
• Пусть даны множества А1, А2, …, Аn и
элементы a1∈А1, a2∈А2,…, an∈Аn .
• Определение 5. Кортежем на множествах
А1, А2, …, Аn называется совокупность
элементов a1, a2,…, an, в которой каждый
элемент занимает определенное место.
• Обозначение: (a1,a2,…,an).

21.

3. Основные определения
• Определение 6. Два кортежа (a1,a2,…,an) и
(b1,b2,…,bn) на множествах А1, А2, …, Аn
называются равными, если ai=bi , где i
=1,2,…,n.
• Элемент ai называется i-той проекцией
(компонентой) кортежа.
• Число n называется длиной кортежа.
• Например, a = (a1, a2 ,…,an) — кортеж длины
n с компонентами a1,a2,…,an.

22.

3. Основные определения
Будем говорить, что множество А
включается во множество В (A B) ,
если каждый элемент множества А
является элементом множества В
(говорят также, что А является
подмножеством множества В).
Из определения включения следуют
свойства:

23.

3. Основные определения
Свойства множеств:
1) A A для любого множества А;
2) Если A B и B С , то A C ;
3) A для любого множества А;
4) A U для любого множества А.
Подмножество A B называется собственным
подмножеством множества В ( A B - строгое
включение), если А не пусто и не совпадает с В.
Например, имеют место строгие включения:
N Z Q R.

24.

3. Основные определения
Равенства множеств
А=В тогда и только тогда, когда одновременно
выполняются два включения A B и B А , т.е.
каждый элемент множества А является
элементом множества В и каждый элемент
множества В является элементом множества А
Свойства равенства множеств:
1)
для любого А справедливо А=A;
2)
если А=В, то и В=A;
3)
если А=В и В=C, то A=C.

25.

4. Диаграмма Эйлера – Венна
Множества удобно изображать с помощью
кругов Эйлера.
Множество K на рис. 1.1 называют
подмножеством множества М и обозначают
K M.
Множество K называется
подмножеством множества
M ( K M ), если для любого
x K выполняется x M .

26.

5. Операции над множествами
Суммой или объединением двух множеств А
и В называется множество, состоящее из
элементов, входящих или во множество А, или
во множество В, а может в оба множества
одновременно (рис. 1.2). Обозначение: Z А В.
U
A
B
(рис. 1.2)

27.

5. Операции над множествами
Операция объединения множеств
обладает следующими свойствами:
• A∪B = B∪A — коммутативность,
• (A∪B)∪C = A∪(B∪C) — ассоциативность,
• A∪Ø = A,
• A∪A = A — идемпотентность,
• A∪I = I.

28.

5. Операции над множествами
Пример
Если A = {0,1,2}, B = {-1,2,3}, то A B {-1,0,1,2,3}.
U
A
B

29.

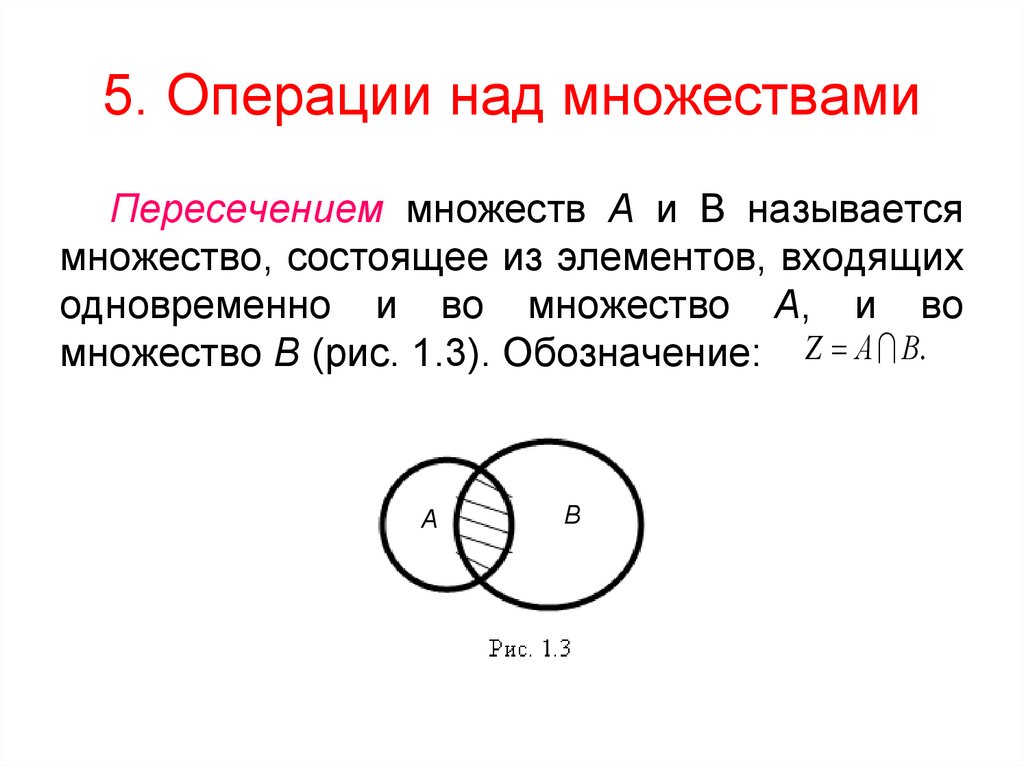
5. Операции над множествами
Пересечением множеств А и В называется
множество, состоящее из элементов, входящих
одновременно и во множество А, и во
множество В (рис. 1.3). Обозначение: Z А В.
А
В

30.

5. Операции над множествами
• Операция пересечения множеств обладает
следующими свойствами:
• A∩B = B∩A,
• (A∩B)∩C = A∩(B∩C),
• A∩A = A,
• A∩Ø = Ø,
• A∩I = A.
• В англоязычной литературе символы ∪ и ∩
называют cap (шляпа).

31.

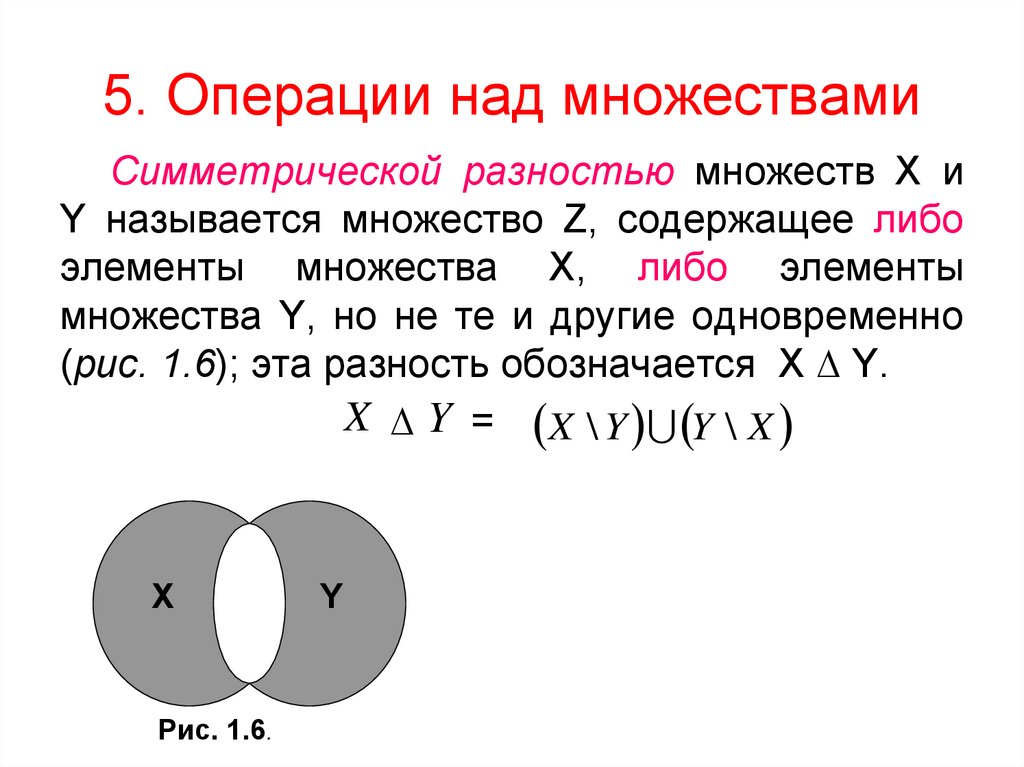
5. Операции над множествами
Разностью множеств А и В называется
множество Z, содержащее все элементы
множества А не содержащиеся в В (рис. 1.4);
эта разность обозначается Z А \ В.
А
В

32.

5. Операции над множествами
Примеры
Пересечение
Если
A = {0,1,2}, B = {-1,2,3}, то A B {2}.
Разность
A \ B {0,1,2} \{-1,2,3} {0,1};
B \ A {-1,2,3} \ {0,1,2} {-1,3}.

33.

5. Операции над множествами
Дополнением
множества X до
X
универсального множества U (рис. 1.5)
является множество X {x | x X , x U }.
i
i
i

34.

5. Операции над множествами
• Операция дополнения обладает следующими
свойствами:
•