Теория вероятностей (1 часть)

1.

2.

Теория вероятностей (1 часть)
• Пример. Сколько времени будет идти маршрутка от
остановки Комсомольская до остановки Дружба – дело
случая. Но Вы должны рассчитать время своего
приезда.
• Пример. То, что застрахованный дом пострадает или
будет уничтожен в течение некоторого периода времени
– дело случая. Но страховой орган должен рассчитывать
сумму страхового взноса за этот период.
• Пример. Все студенты ждут счастливый билет на
экзамене. Попадется ли им он или нет – это дела
случая.
• Но! На практике часто встречаются ситуации, результат
которых трудно спрогнозировать.

3.

Теория вероятностей
Впервые такими ситуациями занялись математики в
середине XVII века. Возникновение теории вероятностей
связано с именами Гюйгенса (1629- 1695), Паскаля (16231662), Ферма (1601-1665) и Якоба Бернулли (1654- 1705) и
другими именами.
При этом лишь азартные игры были главным побудительным
моментом в их деятельности.
Предметом теории вероятностей является изучение
вероятностных закономерностей массовых однородных
случайных событий.

4.

План
Основные понятия теории вероятностей.
I. Испытания и события.
II. Виды случайных событий.
III. Операции над событиями.
IV. Основные формулы комбинаторики.
V. Определения вероятностей. Основные теоремы.
Лекция № 1

5.

Испытания и события
Определения:
1. Опытом или испытанием называют всякое осуществление
комплекса условий или действий, при которых
наблюдается соответствующее явление.
2. Событием называется всякий факт, который может
произойти или не произойти в результате опыта, это исход
некоторого опыта.
3. Каждое событие, которое может наступить в итоге опыта,
называется элементарным исходом ω или шансом
(омега). Извлечение карты «Дама пик» из перемешанной
колоды карт – событие элементарное.
Лекция № 1

6.

Испытания и события
Определения:
1. Событие – это произвольное подмножество
множества элементарных исходов ω.
2. Совокупность всех элементарных исходов опыта
называется пространством элементарных событий
Ω (омега) .
Пример. При подбрасывании монеты пространство
элементарных исходов Ω состоит из двух исходов ω1
или А1 –выпадение «герба или орла», ω2 или А2–
выпадение «цифры или решки».
Лекция № 1

7.

Виды случайных событий
Определения:
1.
2.
3.
4.
События называются несовместными, если появление одного из
них
исключает
появление
других.
Невозможность
одновременного выпадения 2 и 6 при бросании игральной кости.
События называются совместными, если появление одного из
них не исключает появление других. Возможность выпадения
цифры 2 и четной цифры.
Два события называются противоположными, если появление
одного из них равносильно не появлению другого.
Противоположным событием A называется событие, состоящее в
не появлении события Ā. События выпадение «орла» и «решки».
Два события называются равновозможными, если нет оснований
полагать, что одно событие является более возможным, чем
другое. События выпадение «орла» и «решки».
Лекция № 1

8.

Виды случайных событий
Определения:
5. Полной группой событий называется совокупность всех
возможных результатов опыта и обозначают Ω (омега) .
События выпадение «орла», «решки».
6. Достоверным событием называется событие, которое
наверняка произойдет в результате опыта. Событие
выпадения цифры при бросании игральной кости.
7. Событие называется невозможным, если оно никогда не
произойдет в результате опыта. Невозможность
выпадения 7 при бросании игральной кости.
Лекция № 1

9.

Виды случайных событий
Пример оформления:
Бросили игральную (шестигранную) кость (один раз).
Найти …..
Рассмотрим следующие элементарные события:
А1 - бросили игральную кость и выпала «1»;
А2 - бросили игральную кость и выпала «2»;
…
А6 - бросили игральную кость и выпала «6».
Теперь легко представить, что искомое событие A, состоящее
в том, что бросили игральную кость и выпала …
Лекция № 1

10.

Определение вероятностей

11.

Статистическая вероятность. Определение
Относительной частотой события А называется
отношение числа опытов, в результате которых произошло
событие А к общему числу опытов.
Относительной частотой p* случайного события A
называется отношение числа m* появлений данного события
к общему числу n * проведённых испытаний, в каждом из
которых может появиться или нет данное событие:
p*= p*(A) = m*/n*. Чаще всего оказывается (по крайней
мере, теория вероятностей имеет дело именно с такими
частотами, а иные ситуации в ней не рассматриваются), что:
p*= p*(A) = m*/n* → (n* →+∞) → p(A) = p, где p некоторое число: P(A) = m/n
Статистической вероятностью называют число, около
которого колеблется относительная частота события при
большом числе испытаний
Лекция № 1

12.

Классическое определение
вероятности
Определение
Вероятностью события А называется математическая оценка
возможности появления этого события в результате опыта.
Вероятностью события А называют отношение числа
благоприятствующих этому событию исходов к общему числу
всех равновозможных несовместных элементарных исходов,
образующих полную группу:
m
P ( A)
n
Лекция № 1

13.

Задачи на прямое использование
классического определения
вероятности
На тарелке 16 пирожков: 7 с рыбой, 5 с вареньем и 4 с
вишней. Юля наугад выбирает один пирожок. Найдите
вероятность того, что он окажется с вишней.
Решение:
m=4 – число пирожков с вишней (число благоприятных
исходов)
n=16 – число всех пирожков (общее число
равновозможных исходов)
4
P 0 ,25
16

14.

Пример
1. В коробке находится 10 шаров. 3 из них красные, 2 –
зеленые, остальные белые. Найти вероятность того, что
вынутый наугад шар будет красным, зеленым или белым.
Лекция № 1

15.

Задачи на прямое использование
классического определения вероятности
Перед началом первого тура чемпионата по бадминтону
участников разбивают на игровые пары случайным образом с
помощью
жребия.
Всего
в
чемпионате
участвует
26 бадминтонистов, среди которых 10 участников из России, в том
числе Руслан Орлов. Найдите вероятность того, что в первом туре
Руслан Орлов будет играть с каким-либо бадминтонистом из
России?
Решение:
m=10-1=9 – число участников из России за исключением
Руслана Орлова (число благоприятных исходов)
n=26-1=25 – число бадминтонистов, участвующих в
чемпионате за исключением Руслана Орлова (общее число
равновозможных исходов)
9
P
25
0,36

16.

Пример решения задачи
Вероятность того, что новый DVD-проигрыватель в течение года
поступит в гарантийный ремонт, равна 0,045. В некотором городе из
1000 проданных DVD-проигрывателей в течение года в
гарантийную мастерскую поступила 51 штука. На сколько
отличается относительная частота события «гарантийный ремонт»
от его вероятности в этом городе?
Решение. A - событие «гарантийный ремонт»
Частота события A равна М=51, число испытаний N=1000. Тогда
относительная частота события «гарантийный ремонт» равна
51 0,051
W . AТогда
1000
W A P A 0 ,051 0,045 0 ,006

17.

Аксиоматическое определение
вероятности
Аксиома неотрицательности:
Аксиома нормированности:
Аксиома сложения:
Вероятность противоположного события:
Вероятность невозможного события:
Лекция № 1

18.

Задачи на прямое использование
классического определения вероятности
В классе учится 21 человек. Среди них две подруги: Аня и Нина.
Класс случайным образом делят на 7 групп, по 3 человека в
каждой. Найти вероятность того. что Аня и Нина окажутся в
одной группе. Найти вероятность того. что Аня и Нина окажутся
в разных группах.
Решение: Пусть Аня оказалась в некоторой группе, тогда
m=21:7-1=2 – число вакантных мест в этой же группе (число
2
P
0,1
благоприятных исходов)
20
n=21-1=20 – число обучающихся класса за исключением Ани
(общее число равновозможных исходов)
События А – «подруги окажутся в одной группе» и В-«подруги
окажутся в разных группах» являются противоположными. В
этом случае P(A)=1-P(B) = 1- 0,1 = 0,9

19.

Геометрическая вероятность
Классическое определение вероятности неприменимо к
испытаниям с бесконечным числом исходов.
Чтобы преодолеть этот недостаток вводится понятие
геометрической вероятности, т.е. вероятности попадания
точки в какой – либо отрезок или часть плоскости
(пространства).
Лекция № 1

20.

Теорема сложения вероятностей
Лекция № 1

21.

Примеры совместных и несовместных
событий
• Совместные события
Два стрелка делают по одному выстрелу по мишени:
событие А – попадание первого стрелка,
событие В – попадание второго стрелка.
• Несовместные события
Подбрасываем игральный кубик:
событие А – выпадение 1,
событие В – выпадение 5.

22.

Сумма событий
Суммой А + В двух событий А и В называют событие,
состоящее в появлении события А, или события В, или
обоих этих событий.
Если из орудия произведены два выстрела:
событие А — попадание при первом выстреле,
событие В — попадание при втором выстреле,
то событие А + В — попадание при первом выстреле, или
при втором, или в обоих выстрелах.

23.

Теорема о сумме несовместных
событий
Пусть события A и В — несовместные, причем
вероятности этих событий известны.
Теорема. Вероятность появления одного из двух
несовместных событий равна сумме вероятностей этих
событий:
Р (А + В) = Р (А) + Р (В).

24.

Использование теоремы о сумме
несовместных событий
На экзамене по геометрии школьнику достаётся один вопрос из
списка экзаменационных вопросов. Вероятность того, что это
вопрос на тему «Вписанная окружность», равна 0,2, на тему
«Параллелограмм» - 0,15. Вопросов, которые одновременно
относятся к этим двум темам, нет. Найдите вероятность того, что на
экзамене школьнику достанется вопрос по одной из этих двух тем.
Решение:
Пусть событие А – достанется вопрос по теме «Вписанная
окружность», событие В – достанется вопрос по теме
«Параллелограмм»,
Событие А+В – достанется вопрос по одной из этих тем.
События А и В – несовместные, следовательно
P(A+B) =P(A)+P(B) = 0,2+0,15=0, 35

25.

Теорема о сумме совместных событий
Теорема. Вероятность появления хотя бы
одного из двух совместных событий равна сумме
вероятностей этих событий без вероятности их
совместного появления
P(A+B) = P(A) + P(B) — P(AB).
Следствие. Сумма вероятностей противоположных
событий равна единице.

26.

Пример использования теоремы о сумме
совместных событий
В торговом центре два одинаковых автомата продают кофе. Вероятность
того, что к концу дня в автомате закончится кофе, равна 0,25. Вероятность
того, что кофе закончится в обоих автоматах, равна 0,15. Найдите
вероятность того, что к концу дня кофе останется в обоих автоматах.
Тогда
Решение: Пусть
P(A)=P(B)=0,25, P(A*B)=0,15
А – кофе закончится в 1 автомате,
В – кофе закончится во 2 автомате,
А*В – кофе закончится в обоих
автоматах,
событие А+В – кофе закончится
хотя бы в одном автомате,
событие A+B – кофе останется в
обоих автоматах.
События А и В –
совместные, следовательно
P(A+B)=0,25+0,25-0,15=
=0,35.
Таким образом
P(A+B) = 1-0,35=0,65

27.

Произведение событий
Произведением двух событий А и В называют событие А*В,
состоящее в совместном появлении (совмещении) этих событий.
Например, если А — деталь годная,
В — деталь окрашенная,
то А*В — деталь годна и окрашена.
Произведением нескольких событий называют событие, состоящее
в совместном появлении всех этих событий. Например, если А, В,
С — появление «герба» соответственно в первом, втором и
третьем бросаниях монеты, то А*В*С — выпадение «герба» во
всех трех испытаниях.
На практике о независимости событий заключают по смыслу
задачи. Например, вероятности поражения цели каждым из двух
орудий не зависят от того, поразило ли цель другое орудие,
поэтому события «первое орудие поразило цель» и «второе орудие
поразило цель» независимы.

28.

Теорема о произведении независимых
событий
Теорема. В случае независимых событий
вероятность их произведения равна произведению
вероятностей этих событий
Р (А*В) = Р (А) * Р (В)

29.

Использование теоремы о произведении
независимых событий
Если гроссмейстер А. играет белыми, то он выигрывает у
гроссмейстера Б. с вероятностью 0,52. Если А. играет черными, то
А. выигрывает у Б. с вероятностью 0,3. Гроссмейстеры А. и Б.
играют две партии, причем во второй партии меняют цвет фигур.
Найдите вероятность того, что А. выиграет оба раза.
Решение:
Пусть событие А – выигрыш гроссмейстер А. белыми
фигурами, событие В – выигрыш гроссмейстер А. черными
фигурами, событие А*В – выигрыш гроссмейстер А. разными
фигурами.
События А и В – независимые, следовательно
P(A*B) =P(A)*P(B) = 0,52*0,3=0, 156

30.

Условная вероятность
Определения:
1.Событие А называется независимым от события В,
вероятность события А не зависит от того, произошло событие
В или нет.
2.Событие А называется зависимым от события В, если
вероятность события А меняется в зависимости от того,
произошло событие В или нет.
Лекция № 1

31.

Условная вероятность
Определения:
1.Событие А называется независимым от события В,
вероятность события А не зависит от того, произошло
событие В или нет.
2.Событие А называется зависимым от события В, если
вероятность события А меняется в зависимости от того,
произошло событие В или нет.
3.Вероятность события В, вычисленная при условии, что
имело место событие А, называется условной вероятностью
события В.
Лекция № 1

32.

Теорема умножения вероятностей
Вероятность произведения двух событий (совместного
появления этих событий) равна произведению вероятности
одного из них на условную вероятность другого,
вычисленную при условии, что первое событие уже
наступило.
Лекция № 1

33.

Теорема умножения вероятностей
1. Если события независимые, то
,
и теорема умножения вероятностей принимает вид:
2. В случае произведения нескольких зависимых событий
вероятность равна произведению одного из них на условные
вероятности всех остальных при условии, что вероятность
каждого последующего вычисляется в предположении, что
все остальные события уже совершились.
Лекция № 1

34.

Теорема умножения вероятностей
Если в результате испытания может появиться п событий,
независимых в совокупности, то вероятность появления,
хотя бы одного из них равна
Событие А обозначает наступление хотя бы одного из
событий Ai , а qi – вероятность противоположных
событий
Лекция № 1

35.

Задачи на прямое использование
классического определения вероятности
В классе учится 21 человек. Среди них две подруги: Аня и
Нина. Класс случайным образом делят на 7 групп, по
3 человека в каждой. Найти вероятность того, что Аня и
Нина окажутся в одной группе.
Решение по классическому определению:
m=21:7-1=2 – число вакантных мест в этой же группе (число
благоприятных исходов)
n=21-1=20 – число обучающихся класса за исключением Ани
(общее число равновозможных исходов)
2
P 0 ,1
20

36.

Задачи на прямое использование
классического определения вероятности
В классе учится 21 человек. Среди них две подруги: Аня и
Нина. Класс случайным образом делят на 7 групп, по 3 человека в
каждой. Найти вероятность того, что Аня и Нина окажутся в одной
группе.
Вероятность того, что одна из подруг окажется в одной из
3
групп равна 21
Вероятность того, что вторая подруга окажется в этой же
группе равна 2
20
Поскольку все 7 групп равноправны, то вероятность
попасть в одну группу равна
3 2
Р 7 0,1
21 20

37.

Пример
Из полной колоды карт (52 шт.) одновременно вынимают
четыре карты. Найти вероятность того, что среди этих
четырех карт будет хотя бы одна бубновая или одна
червонная карта.
Решение. Обозначим событие А – «появление хотя бы одной
бубновой карты», событие В – «появление хотя бы одной
червонной карты» . Определить вероятность события
С = А + В. События А и В – совместны.
При вытаскивании первой карты вероятность того, что не
появится ни червонной, ни бубновой карты равна 26/52, при
вытаскивании второй карты – 25/51, третьей – 24/50 , четвертой
– 23/49 . Тогда вероятность того, что среди вынутых карт не
будет ни бубновых, ни червонных равна
Тогда
Лекция № 1

38.

Пример
Вероятности того, что нужная деталь находится в первом,
втором, третьем или четвертом ящике, соответственно равны 0,6,
0,7, 0,8, 0,9. Найти вероятности того, что эта деталь находится не
более, чем в трех ящиках.
Решение. Вероятность того, что данная деталь находится во
всех четырех ящиках, равна
Вероятность того, что нужная деталь находиться не более, чем в
трех ящиках равна вероятности того, что она не находится во
всех четырех ящиках
Лекция № 1

39.

Пример. Из районного центра в деревню ежедневно ходит
автобус. Вероятность того, что в понедельник в автобусе
окажется меньше 18 пассажиров, равна 0,82. Вероятность
того, что окажется меньше 10 пассажиров, равна 0,51.
Найдите вероятность того, что число пассажиров будет от
10 до 17.
Количество
пассажиров в
понедельник
Событие А
меньше 10
0, 51
Событие В
от 10 до 17
х
Событие А+В
меньше 18
0,82
События A и B – несовместные, следовательно
0,82=0,51+x. Значит x=0,31

40.

Пример. В магазине стоят два платёжных автомата. Каждый
из них может быть неисправен с вероятностью 0,05
независимо от другого автомата. Найдите вероятность того,
что хотя бы один автомат исправен.
Решение: Пусть
А – неисправен 1 автомат,
В – неисправен 2 автомат,
А*В – неисправны оба автомата,
событие А*В – исправен хотя бы один автомат.
Тогда
P(A)=P(B)=0,05,
События А и В –
независимы
P(A*B)=0,05*0,05=0,0025
Таким образом
P(A*B) = 1-0,0025=0,9975

41.

Примеры решения задач с костями
Игральную кость бросали до тех пор, пока сумма всех выпавших
очков не превысила число 9. Какова вероятность того, что для этого
потребовалось два броска? Ответ округлите до сотых.
Пусть А – событие «за два броска выпало более 9 очков», наступление
события А возможно лишь в трех случаях : выпало 10;11;12 очков.
Пусть В1 - выпало в сумме 10 очков. Это возможно только в трех
случаях 4+6, 6+4, 5+5. Значит , P B1 3 1 1 1
6 6
12
Пусть В2 - выпало в сумме 11 очков. Это возможно только в двух
случаях 5+6, 6+5. Следовательно, P B2 2 1 1 1
6 6
18
Пусть В3 - выпало в сумме
12 очков. Это возможно только в случае
1 1 1
6+6. Поэтому, P B3 6 6 36
Поскольку В1 , В2, В3 и события А =В1+В2 + В3 несовместные,
вероятность их суммы равна сумме вероятностей этих событий:
1
P A P B1 P B2 P B3 0 ,17
6

42.

Пример. При двукратном бросании игральной кости в
сумме выпало 8 очков. Какова вероятность того, что
хотя бы раз выпало 4 очка?
Испытание - бросание кубика.
Выпадение восьми очков при двукратном бросании кубика
возможно только при следующих результатах испытаний:
2+6, 6+2, 3+5, 5+3, 4+4.
Тогда событию А - «выпало восемь очков и хотя бы раз 4»
благоприятствует один исход (m=1), всего исходов пять
(n=5). По определению вероятности получаем, что
m 1
P A
n 5

43.

Пример. Игральную кость бросили два раза. Известно, что
два очка не выпали ни разу. Найдите при этом условии
вероятность события «сумма выпавших очков окажется
равна 4».
Испытание - двукратное бросание кубика. Возможные
исходы испытания занесем в таблицу:
(1;1) (3;1) (4;1) (5;1) (6;1)
(1;3) (3;3) (4;3) (5;3) (6;3)
(1;4) (3;4) (4;4) (5;4) (6;4)
(1;5) (3;5) (4;5) (5;5) (5;6)
(1;6) (3;6) (4;6) (5;6) (6;6)
Здесь m=2, n=25, следовательно, по определению получаем
P A
2
0 ,08
25

44.

Элементы комбинаторики
Комбинаторика - это раздел математики, в котором
изучаются вопросы о том, сколько различных комбинаций,
подчиненных тем или иным условиям, можно составить из
заданных объектов.
Основы комбинаторики очень важны для оценки
вероятностей случайных событий, т.к. именно они
позволяют
подсчитать
принципиально
возможное
количество различных вариантов развития событий.
Лекция № 1

45.

Элементы комбинаторики
Перестановки
предметов
Изучает:
Перебор
возможных
вариантов
Комбинации
предметов

46.

Вспомним несколько примеров таких
задач
1.Несколько стран в качестве символа своего государства
решили использовать флаг в виде 3-х горизонтальных
полос одинаковых по ширине и цвету: синий, красный и
белый. Сколько стран могут испытать такую символику при
условии, что у каждой страны свой отличный от других
флаг?
Будем искать решение с помощью дерева
возможных вариантов.

47.

Ответ : 6 комбинаций

48.

2.Сколько чётных двузначных чисел можно
составить из цифр 0,1,2,4,5,9. Составим таблицу:
слева от 1 – го столбца поместим первые цифры
искомых чисел, сверху – вторые цифры этих чисел
(чётные цифры, тогда столбцов будет три).
Так в столбце перечислены все
возможные
варианты,
следовательно, их столько же,
сколько клеток в столбце, т.е.
15.
Ответ: 15
чисел
0 2 4
1 10 12 14
2 20 22 24
4 40 42 44
5 50 52 54
9 90 92 94

49.

Основная формула комбинаторики
Пусть имеется k групп элементов, причем i-я
группа состоит из ni элементов.
Выберем по одному элементу из каждой
группы.
Тогда общее число N способов, которыми
можно произвести такой выбор, определяется
соотношением
N = n1n2n3...nk
Лекция № 1

50.

Пример
Сколько трехзначных четных чисел можно составить из
цифр 0, 1, 2, 3, 4, 5, 6, если цифры могут повторяться?
Решение: n1= 6 (т.к. в качестве первой цифры можно взять
любую цифру из 1, 2, 3, 4, 5, 6),
n2 = 7 (т.к. в качестве второй цифры можно взять любую
цифру из 0, 1, 2, 3, 4, 5, 6),
n3 = 4 (т.к. в качестве третьей цифры можно взять любую
цифру из 0, 2, 4, 6).
Итак, N = n1*n2*n3= 6*7*4*= 168
Лекция № 1

51.

Основная формула комбинаторики
В том случае, когда все группы состоят из одинакового числа
элементов, т.е. n1= n2=...nk = n можно считать, что каждый
выбор производится из одной и той же группы, причем элемент
после выбора снова возвращается в группу.
Тогда число всех способов выбора равно nk.
Такой способ выбора носит название выборки с возвращением.
Пример.
Сколько всех четырехзначных чисел можно
составить из цифр 1, 5, 6, 7, 8?
Решение. Для каждого разряда четырехзначного числа имеется
пять возможностей, значит
N = 5*5*5*5 = 625
Лекция № 1

52.

Формула комбинаторики
Определение 1. Размещением из n элементов по m называется
любой упорядоченный набор из m различных элементов,
выбранных из генеральной совокупности в n элементов.
Пример. Сколько существует двузначных чисел, в которых
цифра десятков и цифра единиц различные и нечетные?
Решение. Т.к. нечетных цифр пять 1, 3, 5, 7, 9, то задача
сводится к выбору и размещению на две разные позиции двух
из пяти различных цифр, т.е. указанных чисел будет:
Лекция № 1

53.

Формула комбинаторики
Определение 2. Сочетанием из n элементов по m называется
любой неупорядоченный набор из m различных элементов,
выбранных из генеральной совокупности в n элементов.
Пример. Сколькими способами читатель может выбрать две
книжки из шести имеющихся?
Решение. Число способов равно числу сочетаний из шести
книжек по две, т.е. равно:
Лекция № 1

54.

Формула комбинаторики
Определение 3. Перестановкой из n элементов называется
любой упорядоченный набор этих элементов.
Пример 8. Сколькими способами семь книг разных авторов
можно расставить на полке в один ряд?
Решение. Эта задача о числе перестановок семи разных книг.
Имеется
способов осуществить расстановку книг.
Р7
Лекция № 1

55.

Сложение и умножение вероятностей
Пример
В первой урне 12 белых и 4 чёрных шара. Во второй 4 белых
и 5 чёрных шара. Из первой урны вынимают случайным
образом 3 шара, из второй 3. Найти вероятность того, среди
вынутых шаров:
a) все шары одного цвета;
б) только три белых шара;
в) хотя бы один белый шар.
теория вероятностей

56.

Решение:
a)Обозначим событие А: «среди вынутых шаров – все
шары одного цвета».
Тогда события:
А1: «из первой урны вынули 3 белых шара»,
А2: «из второй - 3 белых шара»,
А3: «из первой урны вынули 3 чёрных шара»,
А4: «из второй – 3 чёрных шара».
Так как события А1 и А2, А3 и А4 независимые, то
Р(А1А2) = Р(А1)Р(А2) и Р(А3А4) = Р(А3)P(А4).
Найдём вероятности событий А1, А2, А3, А4:
теория вероятностей

57.

Р(А1 А2) = 0,393*0,048 = 0,1886
теория вероятностей

58.

Так как события ( А1А2) и (А3А4) несовместны, то вероятность
события А находим по теореме сложения:
Р(А) = Р(А1А2) + Р(А3А4).
Получаем
Р(А) = 0,1886 + 0,0008 = 0,1894.
теория вероятностей

59.

б) Обозначим событие В: «среди вынутых шаров – только три
белых».
Рассмотрим все возможные случаи этого события:
В1:«из первой урны вынули 3 белых шара, а из второй – 3
чёрных»;
В2:«из первой урны вынули 2 белых и 1 чёрный шары, а из
второй урны – 1 белый и 2 чёрных»;
В3:«из первой урны вынули 1 белый и 2 черных шара, а из
второй – 2 белых и 1 черный».
В4:«из первой урны вынули 3 чёрных шара , а из второй – 3
белых»;
Так как события В1,В2,В3,В4 несовместны, то вероятность
события В находим по теореме сложения:
Р(В) = Р(В1) + Р(В2) + Р(В3) + Р(В4).
Найдём вероятности событий В1, В2, В3, В4:
теория вероятностей

60.

теория вероятностей

61.

Получаем Р (В) = 0,047 + 0,224 + 0,046 + 0,0003 = 0,3173.
в) Обозначим событие С «среди вынутых шаров – хотя бы
один белый».
Тогда противоположное событию С обозначим
:« среди вынутых шаров – все шары чёрные».
C
теория вероятностей

62.

Задачи на прямое использование
классического определения вероятности
В классе учится 21 человек. Среди них две подруги: Аня и
Нина. Класс случайным образом делят на 7 групп, по
3 человека в каждой. Найти вероятность того, что Аня и
Нина окажутся в одной группе.
Решение по классическому определению:
m=21:7-1=2 – число вакантных мест в этой же группе (число
благоприятных исходов)
n=21-1=20 – число обучающихся класса за исключением Ани
(общее число равновозможных исходов)
2
P 0 ,1
20

63.

Задачи на прямое использование
классического определения вероятности
В классе учится 21 человек. Среди них две подруги: Аня и Нина. Класс
случайным образом делят на 7 групп, по 3 человека в каждой. Найти
вероятность того, что Аня и Нина окажутся в одной группе.
3 способ
3
n C21
количество
Используем формулы комбинаторики:
способов выбрать 3
учащихся из 21
1
m C71 C19
, где
С71 количество способов подругам попасть в одну
1
С19
количество способов добавить в эту
группу
группу 1 из 19 оставшихся
7 19 1
Р
0,1
1330 10

64.

Пример. В первой урне 6 белых и 3 чёрных шара. Во второй 7
белых и 8 чёрных шаров. Из первой урны вынимают случайным
образом 2 шара, из второй 1. Найти вероятность того, среди вынутых
шаров:
a) все шары одного цвета;
б) только три белых шара;
в) хотя бы один белый шар.
Решение:
a)Обозначим событие А «среди вынутых шаров – все шары
одного цвета».
Тогда события:
А1 «из первой урны вынули 2 белых шара»,
А2 «из второй - 1 белый шар»,
А3 «из первой урны вынули 2 чёрных шара»,
А4 «из второй – 1 чёрный шар».
Практикум

65.

Так как события А1 и А2, А3 и А4 независимые, то
Р(А1А2) = Р(А1)Р(А2)
и
Р(А3А4) = Р(А3)P(А4).
Найдём вероятности событий А1, А2, А3, А4:
Практикум

66.

Получаем
Практикум

67.

б) Обозначим событие В «среди вынутых шаров – только три
белых» или В «из первой урны вынули 2 белых шара и из второй
– 1 белый».
Это значит, что событие
В = А1 А2, тогда Р(В) = Р(А1)Р(А2).
Получаем Р(В) = 0,1945.
в) Обозначим событие С «среди вынутых шаров – хотя бы один
белый».
Тогда противоположное событие обозначим С « среди вынутых
шаров – все шары чёрные».
Вероятность события равна Р(А3А4) = 0,0444.
Так как
Р(С) + Р( С) =1, то
Р(С) =1 – 0,0444 = 0,9556.
Ответ:
а) Р(А) = 0,2389;
б) Р(В) = 0,1945;
в) Р(С) = 0,9556.
Практикум

68.

Формула полной вероятности
Пусть некоторое событие А может произойти вместе с
одним из несовместных событий
H1, H2, …, Hn,
составляющих полную группу событий.
Пусть известны вероятности этих событий
P(H1),P(H2),…,P(Hn)
и условные вероятности наступления события А при
наступлении события Hi :
P(A/H1), P(A/H2),…,P(A/Hn).
Практикум

69.

Формула полной вероятности
Пусть событие А может произойти вместе с одним из
независимых событий В1, В2, …. Вn
Обозначим через A/ Bi событие - «событие А произошло
вместе с Bi. Тогда справедлива формула
P A P A / B1 P B1 P A / B2 P B2 P A / Bn P Bn

70.

Теорема
Вероятность события А, которое может произойти вместе с
одним из событий H1,H2,…, Hn,
равна сумме парных произведений вероятностей каждого из
этих событий на соответствующие им условные вероятности
наступления события А.
Практикум

71.

Пример решения задач с
использованием теорем о вероятностях
событий
Две фабрики выпускают
Выпускаемые
одинаковые стекла для
стекла
автомобильных фар. Первая
фабрика выпускает 45% этих
стекол, вторая — 55%. Первая
фабрика выпускает 3%
II-ая фабрика
I-ая
фабрика
45%
бракованных стекол, а вторая —
55%
1%. Найдите вероятность того, что
Брак 3%
случайно купленное в магазине
Брак 1%
стекло окажется бракованным.
P(A+B)=P(A)+P(B)=
=0,03*0,45+0,01*0,55=
=0,019
Событие
А
Событие
В

72.

Пример решения задач с использованием
теорем о вероятностях событий
Всем пациентам с подозрением на гепатит делают
анализ крови. Если анализ выявляет гепатит, то результат
анализа
называется положительным.
У
больных
гепатитом пациентов анализ даёт положительный
результат с вероятностью 0,9. Если пациент не болен
гепатитом, то анализ может дать ложный положительный
результат с вероятностью 0,01. Известно, что 5%
пациентов, поступающих с подозрением на гепатит,
действительно больны гепатитом. Найдите вероятность
того, что результат анализа у пациента, поступившего в
клинику с подозрением на гепатит, будет положительным.

73.

Пример решения задач с использованием
теорем о вероятностях событий
Пациент
Болен гепатитом
5%
Не болен гепатитом
100-5=95%
Положительный
результат
0,9
Ложный положительный
результат
0,01
A – пациент болен и
анализ правильный,
B – пациент здоров и
анализ не правильный
P(A) = 0,05*0,9=0,045
P(B)= 0,95*0,01=0,0095
События А и В –
несовместные
P(A+B)
=0,045+0,0095=0,0545

74.

Пример.
На сборку попадают детали с трех автоматов. Известно, что
первый автомат даёт 3% брака, а второй - 25%, третий - 13%.
Найти вероятность попадания на сборку бракованной детали,
если с первого автомата поступило 1000, со второго-2000 и с
третьего - 1000 деталей.
Решение.
Обозначим событие А «попадания на сборку бракованной
детали».
Гипотезы:
Н1 «с первого автомата поступило 1000 деталей»,
Н2 «со второго-2000 деталей»,
Н3 «с третьего-1000 деталей».
Практикум

75.

Тогда
Р(Н1) = 1000/(1000 + 2000 + 1000) = 0,25,
Р(Н2) = 2000/(1000 + 2000 + 1000) = 0,5,
Р(Н3) = 1000/(1000 + 2000 + 1000) = 0,25 ,
а условные вероятности события А равны
Р(А/Н1) = 3/100 = 0,03,
Р(А/Н2) = 25/100 = 0,25,
Р(А/Н3) = 13/100 = 0,13.
Вероятность события А найдем по формуле
вероятности:
Р(А) = Р(Н1)Р(А/Н1) + Р(Н2)Р(А/Н2) + Р(Н3)Р(А/Н3).
Получаем
Ответ: Р(А) = 0,165.
Практикум
полной

76.

Формула Бейеса.
(формула гипотез)
Пусть имеется полная группа несовместных гипотез
H1, H2, …, Hn с известными вероятностями их
наступления P(H1),P(H2),…,P(Hn).
Пусть в результате опыта наступило событие А,
условные вероятности которого по каждой из гипотез
известны, т.е. известны вероятности P(A/H1),P(A/H2),
…,P(A/Hn).
Требуется определить какие вероятности имеют
гипотезы относительно события А, т.е. условные
вероятности P (H1 /A), P(H2/A),…,P(Hn /A)
Практикум

77.

Теорема
Вероятность гипотезы после испытания равна произведению
вероятности гипотезы до испытания на соответствующую ей
условную вероятность события, которое произошло при
испытании, деленному на полную вероятность этого
события.
Практикум

78.

Задание 2.
На сборку попадают детали с трех автоматов. Известно, что
первый автомат даёт 3% брака, а второй - 25%, третий - 13%.
Найти вероятность попадания на сборку бракованной детали
изготовленной первым, вторым или третьим автоматом, если с
первого автомата поступило 1000, со второго-2000 и с третьего1000 деталей.
Решение.
Обозначим событие А «на сборку попадает бракованная
деталь».
Гипотезы:
Н1 «с первого автомата поступило 1000 деталей»,
Н2 «со второго-2000 деталей»,
Н3 «с третьего-1000 деталей».
Практикум

79.

Тогда
Р(Н1) = 1000/(1000 + 2000 + 1000) = 0,25,
Р(Н2) = 2000/(1000 + 2000 + 1000) = 0,5,
Р(Н3) = 1000/(1000 + 2000 + 1000) = 0,25 ,
а условные вероятности события А равны
Р(А/Н1) = 3/100 = 0,03,
Р(А/Н2) = 25/100 = 0,25,
Р(А/Н3) = 13/100 = 0,13.
Вероятность события А найдем по формуле полной
вероятности:
Р(А) = Р(Н1)Р(А/Н1) + Р(Н2)Р(А/Н2) + Р(Н3)Р(А/Н3).
Получаем
Практикум

80.

Найдем искомые вероятности по формуле Байеса:
Контроль
P (H1 /A) + P(H2/A) + P(H3 /A) = 1,
0.0454+ 0.7576 + 0.1970 = 1 .
Ответ: искомые вероятности равны 0.0454 , 0.7576 , 0.1970.
Практикум

81.

Пример.
В батарейной системе зажигания состоящей из аккумуляторной
батареи (АБ), катушки зажигания (КЗ), распределителя
зажигания (РЗ) и свечей зажигания (СЗ) вышли из строя два
элемента.
Найти вероятность того, что неисправны элементы:
1)катушка зажигания и аккумуляторная батарея;
2)аккумуляторная батарея и распределитель зажигания;
3)катушка зажигания и распределитель зажигания;
4)аккумуляторная батарея и свечи зажигания;
5)распределитель зажигания и свечи зажигания;
6)катушка зажигания и свечи зажигания, если известна
вероятность отказа АБ, КЗ, РЗ, СЗ соответственно равна
p1 = 0,35, p2 = 0,15, p3 = 0,2, p4 = 0,3.
теория вероятностей

82.

Решение: Обозначим событие А «в батарейной системе
зажигания вышли из строя два элемента».
Тогда обозначим гипотезы:
Н1:«неисправны катушка зажигания и аккумуляторная
батарея»,
Н2:«неисправны аккумуляторная батарея и распределитель
зажигания»,
Н3:«неисправны катушка зажигания и распределитель
зажигания»,
Н4:«неисправны аккумуляторная батарея и свечи зажигания»,
Н5:«неисправны
распределитель
зажигания
и
свечи
зажигания»,
Н6:«неисправны катушка зажигания и свечи зажигания».
теория вероятностей

83.

Так как по условию не дается предпочтение ни одной из
гипотез, то их вероятности равны:
Р(Н1) = Р(Н2) = Р(Н3) = Р(Н4) = Р(Н5) = Р(Н6) = 1/6
АБ,
КЗ,
РЗ,
СЗ
По условию задачи p1 = 0,35, p2 = 0,15, p3 = 0,2, p4 = 0,3,
так как р + q = 1, то q1 = 0,65, q2 = 0,85, q3 = 0,8, q4 = 0,7.
Найдем условные вероятности события А:
теория вероятностей

84.

Найдем вероятность события А по формуле полной
вероятности:
Получаем
теория вероятностей

85.

Так как события Нk/А, где k = 1,2,3,4,5,6, cоставляют
полную группу, то
0,138 + 0,196 + 0,064 + 0,336 + 0,156 + 0,110 = 1.
теория вероятностей

86.

Задание 4.
Проверка качества выпускаемых деталей показала, что в
среднем брак составляет 3 %. Найти наиболее вероятное число
стандартных деталей в партии из 30 штук, отобранных
наудачу.
Ответ: 30 деталей наиболее вероятное число стандартных
деталей в партии из 30 штук.
Практикум

87.

Повторение испытаний.
Формула Бернулли
Если производится некоторое количество испытаний, в
результате которых может произойти или не произойти событие
А, и вероятность появления этого события в каждом из
испытаний не зависит от результатов остальных испытаний, то
такие испытания называются независимыми относительно
события А.
Допустим, что событие А наступает в каждом испытании с
вероятностью Р(А) =р и не наступает с вероятностью q = 1 - p .
Определим вероятность Рп (m) того, что в результате п
испытаний событие А наступило ровно т раз.
Практикум

88.

Задача 3. Для нормальной работы автобазы на линии
должно быть не менее 5 машин, а имеется их 8.
Вероятность невыхода каждой машины на линию равна 0,3.
Найти вероятность нормальной работы автобазы на
ближайший день.
Решение.
Обозначим событие А «нормальная работа автобазы на
ближайший день».
Это значит что на линии должно быть 5, 6, 7, 8 машин.
Тогда вероятность события А найдем по формуле
Р(А) = Р8(5) + Р8(6) + P8(7) + Р8(8).
Вероятности Рn(m) найдем по формуле Бернулли:
Практикум

89.

Найдем вероятности выхода на линию 5, 6, 7, 8 машин:
Получаем
Р(А) = 0,254 + 0,296 + 0,198 + 0,058 = 0,806.
Ответ: Р(А) = 0,806.
Практикум

90.

Схема Бернулли
Задача 5.
Для нормальной работы автобазы на линии должно быть
не менее 7 машин, а имеется их 9. Вероятность невыхода
каждой машины на линию равна 0,3. Найти вероятность
нормальной работы автобазы на ближайший день.
теория вероятностей

91.

Локальная формула Лапласа
Практикум

92.

Интегральная формула Лапласа
Практикум

93.

Задание 5.
Производство карбюраторов даёт брак с вероятностью 0.2.
Какова вероятность того, что из проверенных 176
карбюраторов выбракованных будет не более 17?
Решение.
Воспользуемся интегральной теоремой Лапласа:
Pn(m1, m2) = Ф(х2) – Ф(х1),
где Ф(х)- интегральная функция Лапласа,
По условию, n = 176, p = 0.2, q = 1 – 0.2 = 0.8; m1= 0, m2 =17.
Практикум

94.

Вычислим х1 и х2.
Учитывая, что функция Лапласа нечетная, т. е. Ф( –х) = – Ф(х),
получим
Р176(0; 17) = Ф(– 3.43) – Ф(– 6.63) = – Ф(3.43) + Ф(6.63) =
= – 0.49966 + 0.5 = 0.00034.
Ответ: Р176(0; 17) = 0.00034.
Практикум

95.

Задача . Вероятность появления положительного результата
в каждом из n опытов равна 0,76. Сколько нужно произвести
опытов, чтобы с вероятностью 0,94 можно было ожидать, что
не менее 340 опытов дадут положительный результат.
Решение.
По условию р = 0,76, q = 1 – 0,76 = 0,24, m1 = 340, m2 = n,
Pn(m1,m2) = 0,94.
Используем интегральную теорему Лапласа:
Pn(m1,m2) = Φ(x2) – Φ(x1),
где

96.

97.

98.

Формула Пуассона.
(Симеон Дени Пуассон (1781 – 1840) – французский математик)
Пусть производится п независимых испытаний, в которых
появление события А имеет вероятность р.
Если число испытаний п достаточно велико, а вероятность
появления события А в каждом испытании мало (p 0,01), то
вероятность появления события А m раз находится по
формуле Пуассона.
Практикум

99.

Задача 6.
Завод отправил на базу 400 изделий. Вероятность
повреждения изделий в пути равна 0,001. Найти вероятность
повреждения того, что в пути будет повреждено изделий:
а) ровно 4; б) менее 4; в) более 4; г) хотя бы одно.
Решение.
а) Обозначим событие А «в пути повреждено ровно 4
изделия». Так как n = 400 велико, а вероятность повреждения
изделий p = 0,001 мала, то вероятность события А найдем по
формуле Пуассона
где
Практикум

100.

Получаем, тогда λ = 400 ∙ 0,001 = 0,4
Р(А) = Р400 (4) = 0,44 e – 0,4/4! = 0,0007.
б) Обозначим событие В «в пути повреждено менее 4 изделий».
Р400 (m < 4) = P400 (0) + P400 (1) + P400 (2) + P400 (3);
P(В) = 0,4 e–0,4/0! + 0,4 e–0,4/1! + 0,42e–0,4/2! + 0,43e–0,4/3! =
= e – 0,4 (1 + 0,4 + 0,08+ + 0,01) = 0,9987.
в) Обозначим событие С «в пути повреждено более 4 изделий».
Р400(m > 4) = 1 – [P400 (0) + P400 (1) + P400 (2) + P400 (3) +
+ P400 (4)],
P(С) = 1 – (0,9987 + 0,0007) = 1 – 0,9994 = 0,0006.
Практикум

101.

Практикум

102.

Случайные величины
Практикум

103.

Элементы теории вероятностей
(часть 2)
• Способы задания случайных величин
• Числовые характеристики
• Основные дискретные распределения
• Основные непрерывные распределения

104.

Определение. Случайной величиной называют величину, которая в результате испытания примет одно и
только одно возможное значение, наперёд не известное и зависящее от случайных причин, которые
заранее не могут быть учтены.
Примеры.
1. Количество родившихся мальчиков среди 100
новорождённых.
2. Расстояние, которое пролетит снаряд при выстреле.
Дискретные и непрерывные случайные величины.
Случайные величины: X, Y, Z,…, их значения: x, y, z,…

105.

Определения:
Дискретной случайной величиной называется
такая величина, которая в результате опыта может
принимать определенные значения с
определенной вероятностью, образующие счетное
множество (множество, элементы которого могут
быть занумерованы).
Непрерывной случайной величиной называется
такая величина, которая может принимать любые
значения из некоторого конечного или
бесконечного промежутка.

106.

Определение. Законом распределения дискретной
случайной величины называют соответствие между
возможными значениями случайной величины и их
вероятностями.
Таблично, ряд распределения:
X
x1
x2
…
xn
p
p1
p2 …
pn
p1+ p2 +…+ pn= 1
Аналитически:
p( xi ) f (i ), i 1, 2, ..., n

107.

Определение. Законом распределения дискретной
случайной величины называют соответствие между
возможными значениями случайной величины и их
вероятностями.
Графически:
X
x1
x2
…
xn
p
p1
p2 …
pn
p1
x1
p2
x2
p3
x3
p4
x4
– многоугольник
распределения

108.

Пусть дискретная случайная величина Х задана
своим законом распределения:
Многоугольником распределения вероятностей данной
величины называют ломаную, звенья которой
соединяют соседние точки (хi, pi).

109.

110.

Пример. По цели производится 5 выстрелов. Вероятность
попадания для каждого выстрела равна 0,4. Найти вероятности
числа попаданий и построить многоугольник распределения.
Решение.
Вероятности попаданий из пяти возможных, находим по
формуле Бернулли и равны соответственно:
Практикум

111.

Закон распределения дискретной
случайной величины
X
0
1
2
3
4
5
p
0,0778
0,2592
0,3456
0,2304
0,0768
0,0102
р = 0,0778+0,2592+0,3456+0,2304+0,0768+0,0102 = 1
Практикум

112.

Графическая зависимость числа попаданий от их
вероятностей.
0,4
0,35
0,3
0,25
0,2
0,15
0,1
0,05
0
0
1
2
Практикум
3
4
5

113.

p( X x )
x1
x2
x
Определение. Функцией распределения случайной
величины Х называется функция F(x), задающая
вероятность того, что случайная величина Х
принимает значение, меньшее x, то есть
F(x) = p(X < x).
Иногда функцию F(x) называют интегральной
функцией распределения.
Определение. Случайная величина Х называется
непрерывной, если её функция распределения
непрерывна на всей числовой оси.

114.

Свойства функции распределения:
1) 0 F ( x ) 1
2) Если x1 < x2, то
F ( x1 ) F ( x 2 )
3) p ( a x b) F (b) F ( a )
4) Если возможные значения случайной величины
принадлежат интервалу (a, b), то а) F(x)=0 при x a
и б) F(x)=1 при x b
5) Если Х – непрерывная случайная величина, то
вероятность того, что она примет одно
определённое значение равна нулю: p(X=x) = 0.

115.

Функция распределения дискретной случайной величины Х
разрывная и возрастает скачками при переходе через каждое
значение хi.
Пример. Испытывается устройство, состоящее из четырех
независимо работающих приборов. Вероятности отказа
каждого из приборов равны соответственно р1=0,3; p2=0,4;
p3=0,5; p4=0,6. Найти функцию распределения случайной
величины – числа отказавших приборов.
Решение. Принимаем за случайную величину число
отказавших приборов, значения которой 0, 1, 2, 3 или 4.
Для составления закона распределения этой случайной
величины
необходимо
определить
соответствующие
вероятности.
Лекция

116.

р1 = 0,3; p2 = 0,4;
q1 = 0,7; q2 = 0,6;
p3=0,5;
q3=0,5;
p4=0,6
q4=0,4
1) Не отказал ни один прибор:
p (0) q1q2 q3 q4 0, 7 0, 6 0, 5 0, 4 0, 084.
2) Отказал один прибор:
p (1) p1q2 q3 q4 q1 p2 q3 q4 q1q2 p3 q4 q1q2 q3 p4
3) Отказали два прибора:
p (2) p1 p2 q3q4 p1q2 p3 q4 p1q2 q3 p4 q1 p2 p3 q4 q1 p2 q3 p4 q1q2 p3 p4
4) Отказали три прибора:
p (3) p1 p2 p3 q4 p1 p2 q3 p4 p1q2 p3 p4 q1 p2 p3 p4
5) Отказали все приборы:
p (4) p1 p2 p3 p4
Лекция

117.

Получаем закон распределения:
x
0
1
2
3
4
P
0,084
0,302
0,38
0,198
0,036
(-∞,0)
[0, 1)
[1,2)
[2,3)
[3,4)
[4, +∞)
F(x)
0,084
0,084+ 0,084+
0,302=0, 0,302+
386
0,38=0,
766
0,084+
0,302+
0,38+
0,198
0,084+
0,302+
0,38+
0,198+
0,036=1
1
Функция
распределения
будет иметь вид:
0,8
0,6
0,4
0,2
0
Функция
распределения
0
1
2
3
4
0,084
0,386
0,766
0,964
1
Лекция

118.

Определение.
Плотностью
распределения
вероятностей непрерывной случайной величины
Х называют функцию, являющуюся производной
от функции распределения:
f (x) = F’(x) =lim (F(x))=A
Также функцию f(x) называют плотностью
вероятности или дифференциальной функцией
распределения.

119.

Свойства функции плотности распределения:
b
1) p ( a x b) f ( x )dx
x
a
2) F ( x ) f ( x )dx
p(a < x < b)
f (x)
a
b
3) f ( x ) 0
4)
f ( x )dx 1
f (x)

120.

Получаем закон распределения:
x
0
1
2
P
F(x)
3
4
0,084
0,302
0,38
0,198
0,036
[0, 1)
[1,2)
[2,3)
[3,4)
[4,…)
0,084
0,084+
0,302
0,084+
0,302+
0,38
0,084+
0,302+
0,38+
0,198
0,084+
0,302+
0,38+
0,198+
0,036=1
1
Функция
распределения
будет иметь вид:
0,8
0,6
0,4
0,2
0
Функция
распределения
0
1
2
3
4
0,084
0,386
0,766
0,964
1
Лекция

121.

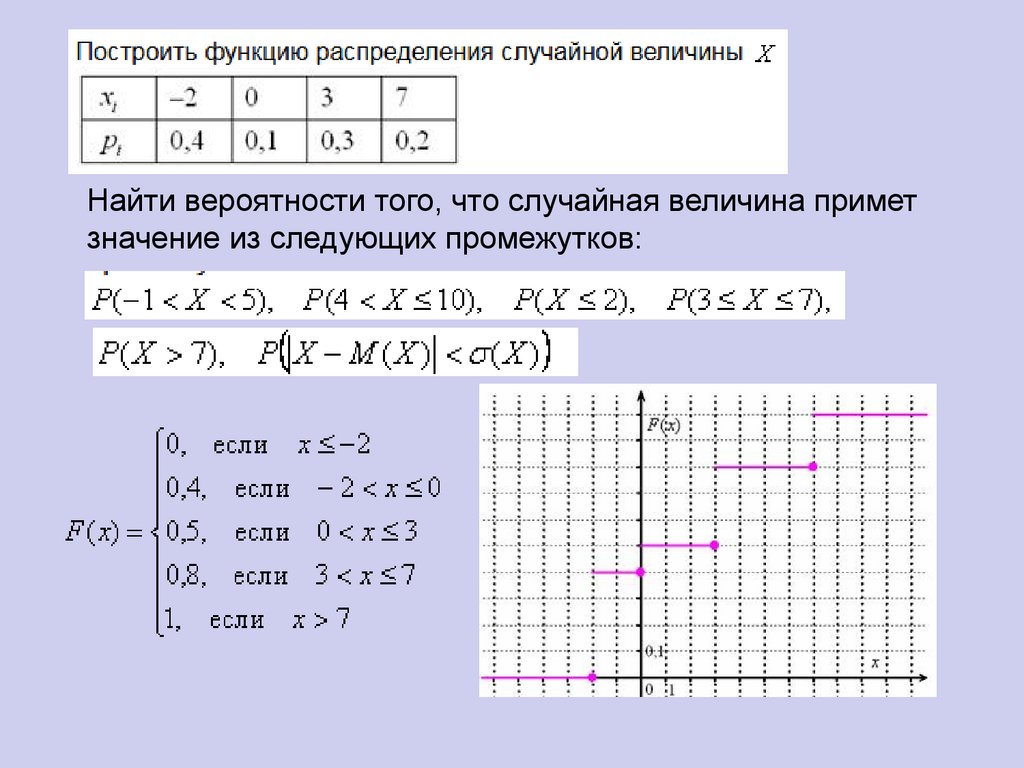
Найти функцию распределения
случайной величины

122.

Найти вероятности того, что случайная величина примет
значение из следующих промежутков:

123.

Пример.
Случайная
величина
распределения с плотностью: .
подчинена
закону
Требуется найти коэффициент а, построить график функции
плотности распределения, определить вероятность
того, что
случайная величина попадет в интервал от 0 до 4 .
Решение.
Для нахождения коэффициента а воспользуемся свойством
f ( x)dx 1
Лекция

124.

Пример. Задана непрерывная случайная величина х
своей
плотностью
распределения
f(x).
A
cos
2
x
,
при
x
4
4
f ( x)
0,
при
x
4
Требуется определить коэффициент А, найти функцию
распределения, построить графики функции распределения и
плотности распределения, определить вероятность того, что
случайная величина х попадет в интервал .
Решение. Найдем коэффициент А
Найдем функцию распределения:
1) На участке
Лекция

125.

2) На участке
3) На участке
Итого:
Лекция

126.

График плотности распределения:
1
0.8
0.6
0.4
0.2
-0.75
-0.5
-0.25
0.25
Лекция
0.5
0.75

127.

График функции распределения:
1
0.8
0.6
0.4
0.2
-0.75
-0.5
-0.25
0.25
Лекция
0.5
0.75

128.

Найдем вероятность попадания случайной величины в
интервал
Ту же самую вероятность можно искать и другим способом:
Лекция

129.

Определение. Математическим ожиданием
дискретной случайной величины Х называют
сумму произведений всех возможных значений
этой случайной величины на соответствующие им
вероятности. Обозначается М(Х).
Пусть
X
p
x1
p1
x2 …
p2 …
xn
pn
М(Х)= x1p1 +х2p2+…хnpn
Если случайная величина Х принимает бесконечное
множество значений, то
M ( X ) x i pi
i 1

130.

Свойства математического
ожидания
1) Математическое ожидание постоянной величины равно
самой постоянной.
2) Постоянный множитель можно выносить за знак
математического ожидания.
3) Математическое ожидание произведения двух
независимых случайных величин равно произведению их
математических ожиданий.
4) Математическое ожидание суммы двух случайных
величин равно сумме математических ожиданий слагаемых.
Лекция

131.

Пусть производится п независимых испытаний, вероятность
появления события А в которых равна р.
Теорема. Математическое ожидание М(Х) числа появления
события А в п независимых испытаниях равно произведению
числа испытаний на вероятность появления события в каждом
испытании.
Отклонение значений случайной величины от математического
ожидания равно разности между случайной величиной и ее
математическим ожиданием.
Математическое ожидание отклонения равно нулю.
Лекция

132.

Определение. Математическим ожиданием
непрерывной случайной величины Х, возможные
значения которой принадлежат отрезку [a, b],
называется определённый интеграл
b
M ( X ) xf ( x )dx
a
Если возможные значения случайной величины
распределены по всей оси Ox, то
M ( X ) xf ( x )dx

133.

(X–М(Х))2
(x1–М(Х))2
(x2–М(Х))2
…
(xn–М(Х))2
p
p1
p2
…
pn
Определение. Дисперсией случайной величины Х
называют математическое ожидание квадрата
отклонения случайной величины Х от её
математического ожидания:
D ( X ) M [ X M ( X )] 2
D ( X ) ( xi M ( X )) 2 pi
i
D ( X ) M ( X 2 ) [ M ( X )] 2

134.

Непрерывная случайная величина
По определению
b
D ( X ) M [ X M ( X )] 2
Но M ( X ) xf ( x )dx
a
b
2
(
x
M
(
X
))
f ( x )dx
M [ X M ( X )]
2
b
a
D ( X ) ( x M ( X )) 2 f ( x )dx
a
b
D ( X ) x 2 f ( x )dx [ M ( X )] 2
a

135.

Свойства дисперсии
1) Дисперсия постоянной величины равна нулю.
2) Постоянный множитель можно выносить за знак дисперсии,
возводя его в квадрат.
3) Дисперсия суммы двух независимых случайных величин
равна сумме дисперсий этих величин.
4) Дисперсия разности двух независимых случайных величин
равна сумме дисперсий этих величин.
Лекция

136.

Теорема. Дисперсия числа появления события А в п
независимых испытаний, в каждом из которых
вероятность р появления события постоянна, равна
произведению числа испытаний на вероятности
появления и не появления события в каждом
испытании.
Пример.
Завод выпускает 96% изделий первого сорта и 4% изделий
второго сорта. Наугад выбирают 1000 изделий. Пусть Х –
число изделий первого сорта в данной выборке. Найти
закон распределения, математическое ожидание и
дисперсию случайной величины Х.

137.

Решение.
Выбор каждого из 1000 изделий можно считать независимым
испытанием, в котором вероятность появления изделия
первого сорта одинакова и равна р = 0,96.
Таким образом, закон распределения может считаться
биноминальным.
Лекция

138.

Пример. Две игральные кости одновременно бросают 2 раза.
Написать биноминальный закон распределения дискретной
случайной величины Х – числа выпадений четного числа очков
на двух игральных костях. Найти математическое ожидание и
дисперсию случайной величины.
Решение. Вероятность выпадения четного числа очков на одной
кости равна 0,5.
Вероятность одновременного выпадения четных очков на двух
костях равна 0,25.
Вероятность того, что при двух испытаниях оба раза выпали
четные очки на обеих костях, равна:
Вероятность того, что при двух испытаниях один раз выпали
четные очки на обеих костях:
Вероятность того, что при двух испытаниях ни одного раза не
выпало четного числа очков на обеих костях:
Лекция

139.

Закон распределения случайной величины имеет вид:
X
p
0
0.0625
1
0.375
2
0.5625
Математическое ожидание случайной величины равно:
Возможные значения квадрата отклонения:
[X-M(X)]2
p
2,25
0,0625
0,25
0,375
0,25
0,5625
Дисперсия равна: D(X) = 2,25*0,0625+0,25*0,375+0,25*0,5625=
=0,375
σ = 0,612
Лекция

140.

Применим формулу
X
X2
p
0
0
1
1
0.0625
2
4
0.375
Лекция
0.5625

141.

Среднее квадратическое отклонение
Определение. Средним квадратическим отклонением случайной величины Х называют корень из её
дисперсии:
( X ) D( X )

142.

Пример.
Производятся независимые испытания с одинаковой
вероятностью появления события А в каждом испытании.
Найти вероятность появления события А, если среднее
квадратическое отклонение числа появлений события в трех
независимых испытаниях равно 0,794.
Решение.
По определению среднего квадратического отклонения
находим дисперию D(X) = ϭ2, тогда D(X) = 0,63.
По формуле дисперсии биноминального закона получаем:
Лекция

143.

Пример.
Завод выпускает 96% изделий первого сорта и 4%
изделий второго сорта. Наугад выбирают 1000 изделий.
Пусть Х – число изделий первого сорта в данной выборке. Найти
закон распределения, математическое ожидание и дисперсии
случайной величины Х.
Решение.
Выбор каждого из 1000 изделий можно считать независимым
испытанием, в котором вероятность появления изделия первого
сорта одинакова и равна р = 0,96.
Следовательно, закон распределения можно считать
биноминальным.
Лекция

144.

Пример. Задана непрерывная случайная величина х своей
плотностью распределения f(x).
cos 2 x, ï ðè
f ( x )
0,
ï ðè
x
4
4
x
4
Определить математическое ожидание, дисперсию и среднее
квадратическое отклонение непрерывной случайной величины Х.
Решение.
Лекция

145.

Лекция

146.

Лекция

147.

Лекция