Похожие презентации:
Графы. Решение логических задач с помощью графов (7 класс)
1.
Графы.Решение логических задач с помощью
графов.
2.
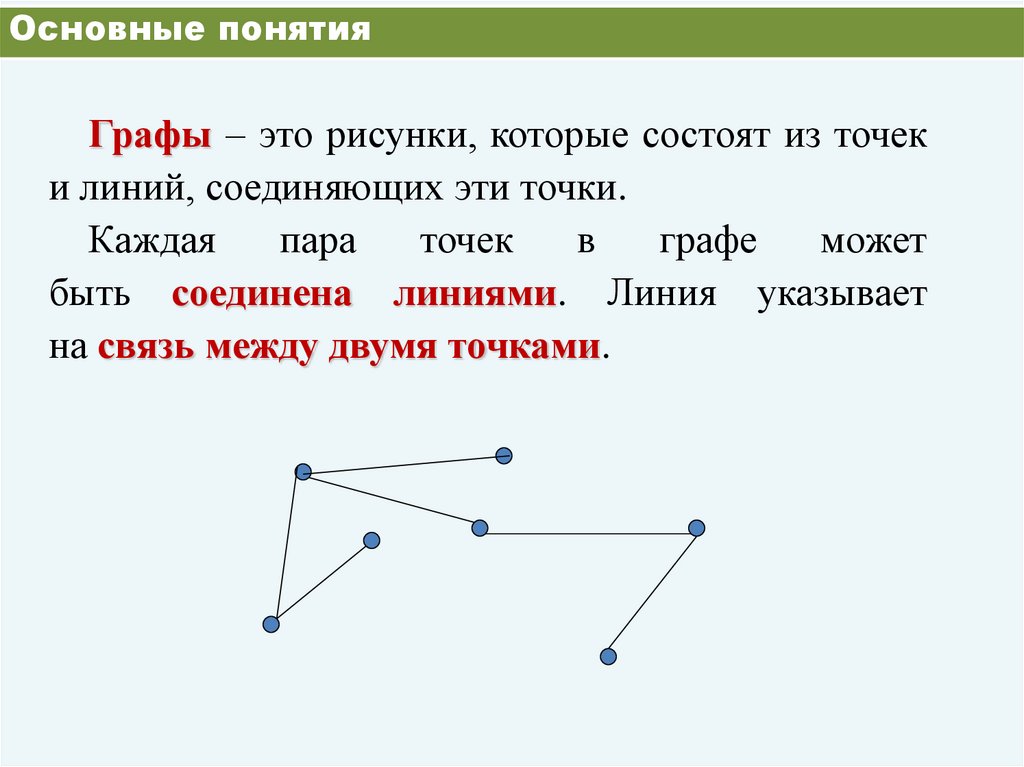
Основные понятияГрафы – это рисунки, которые состоят из точек
и линий, соединяющих эти точки.
Каждая
пара
точек
в
графе
может
быть соединена линиями. Линия указывает
на связь между двумя точками.
3.
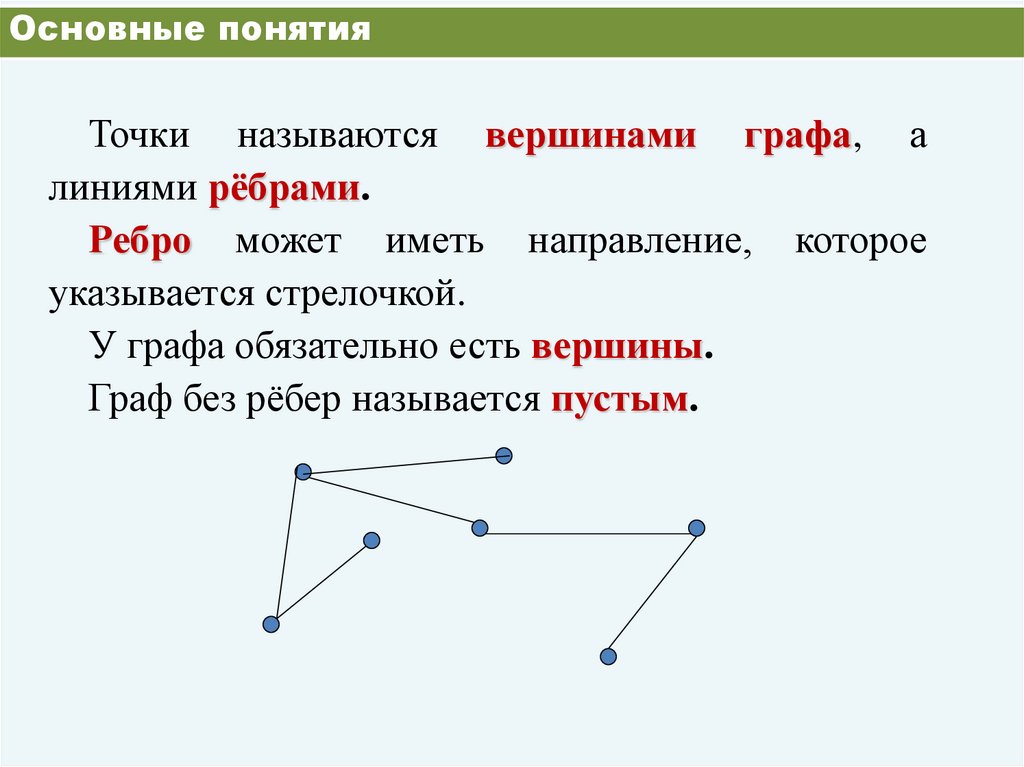
Основные понятияТочки называются вершинами графа, а
линиями рёбрами.
Ребро может иметь направление, которое
указывается стрелочкой.
У графа обязательно есть вершины.
Граф без рёбер называется пустым.
4.
Основные понятияНаправленная линия (со
стрелкой) называется дуга.
Линия ненаправленная
(без стрелки) называется
ребро.
Линия, выходящая из
некоторой вершины и
входящая в неё же,
называется петля.
А
дуга
ребро
петля
В
С
А,В,С – вершины графа
5.
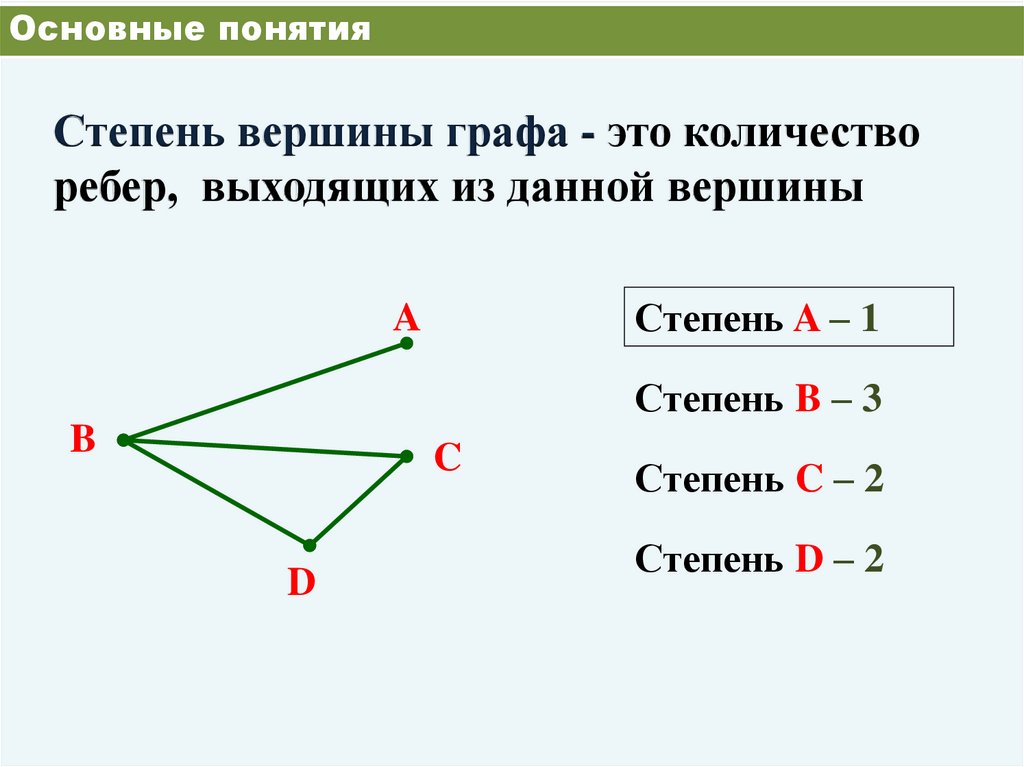
Основные понятияСтепень вершины графа - это количество
ребер, выходящих из данной вершины
Степень A – 1
A
Степень B – 3
B
C
D
Степень C – 2
Степень D – 2
6.
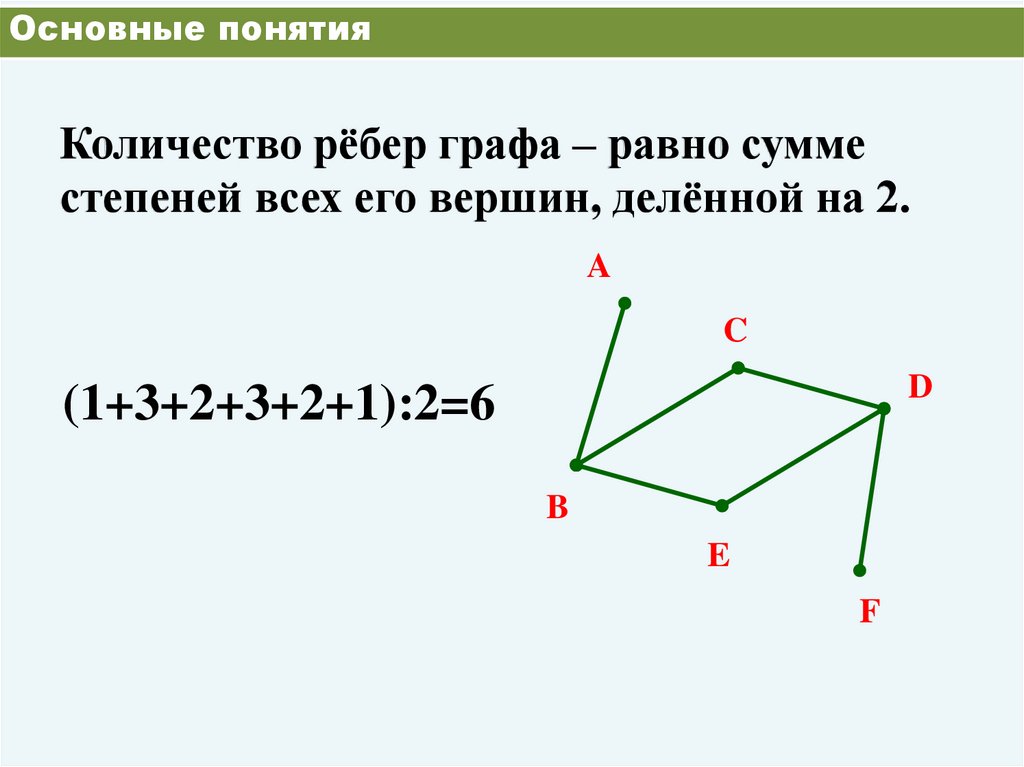
Основные понятияКоличество рёбер графа – равно сумме
степеней всех его вершин, делённой на 2.
A
C
D
(1+3+2+3+2+1):2=6
B
E
F
7.
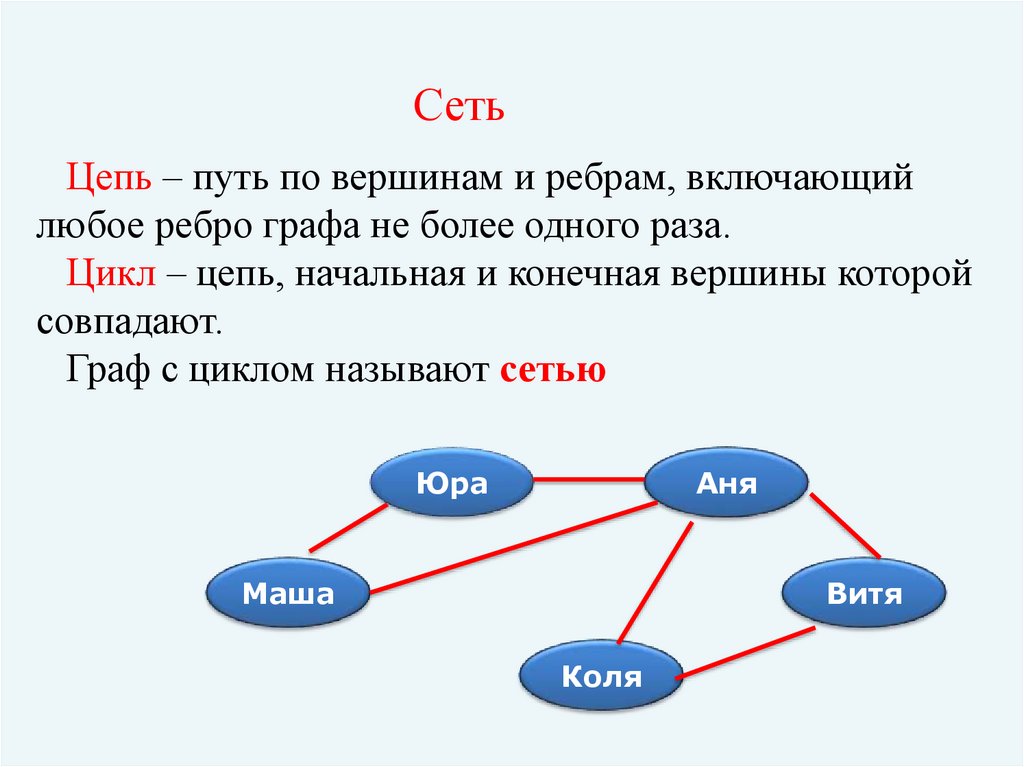
Какие бывают графы?Неориентированный граф
Неориентированный граф - граф, вершины
которого соединены ребрами.
С помощью таких графов могут быть представлены схемы
двухсторонних (симметричных) отношений.
Юра
Аня
Маша
Коля
Витя
Граф, отражающий отношение «переписываются» между
объектами класса «дети»
8.
Какие бывают графы?Ориентированный граф (орграф)
Ориентированный граф - граф, вершины которого
соединены дугами.
С помощью таких графов могут быть представлены схемы
односторонних отношений.
Юра
Аня
Маша
Коля
Витя
Граф, отражающий отношение «пишет письма».
9.
Какие бывают графы?Взвешенный граф
Взвешенный граф - граф, у которого вершины или
рёбра (дуги) несут дополнительную информацию
(вес).
182
127
158
Москва, 1147
Владимир, 1108
Переславль Залесский, 1152
10.
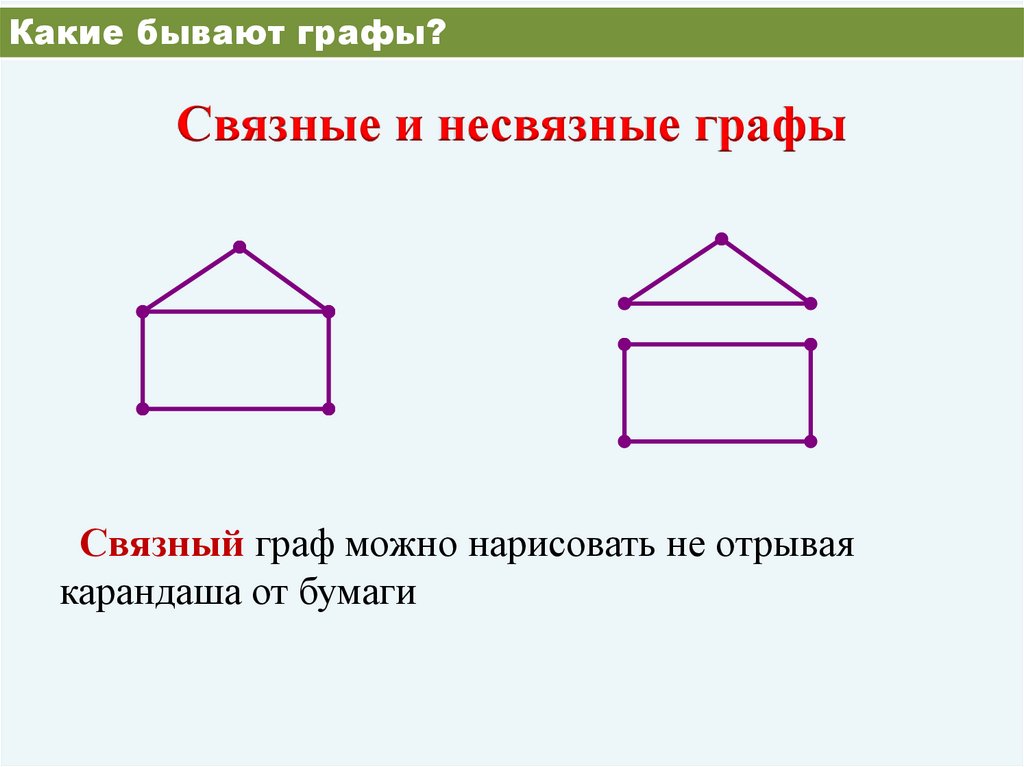
Какие бывают графы?Связные и несвязные графы
Связный граф можно нарисовать не отрывая
карандаша от бумаги
11.
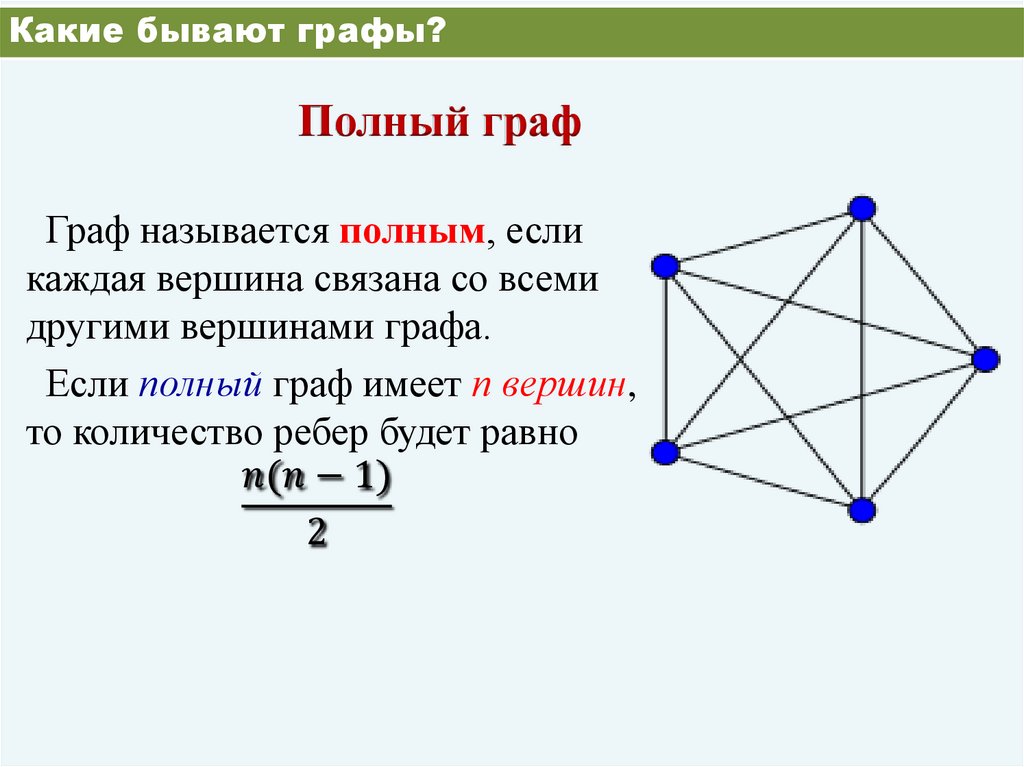
Какие бывают графы?Полный граф
Граф называется полным, если
каждая вершина связана со всеми
другими вершинами графа.
Если полный граф имеет n вершин,
то количество ребер будет равно























 Математика
Математика








