Подготовка к МЦКО (9 класс)

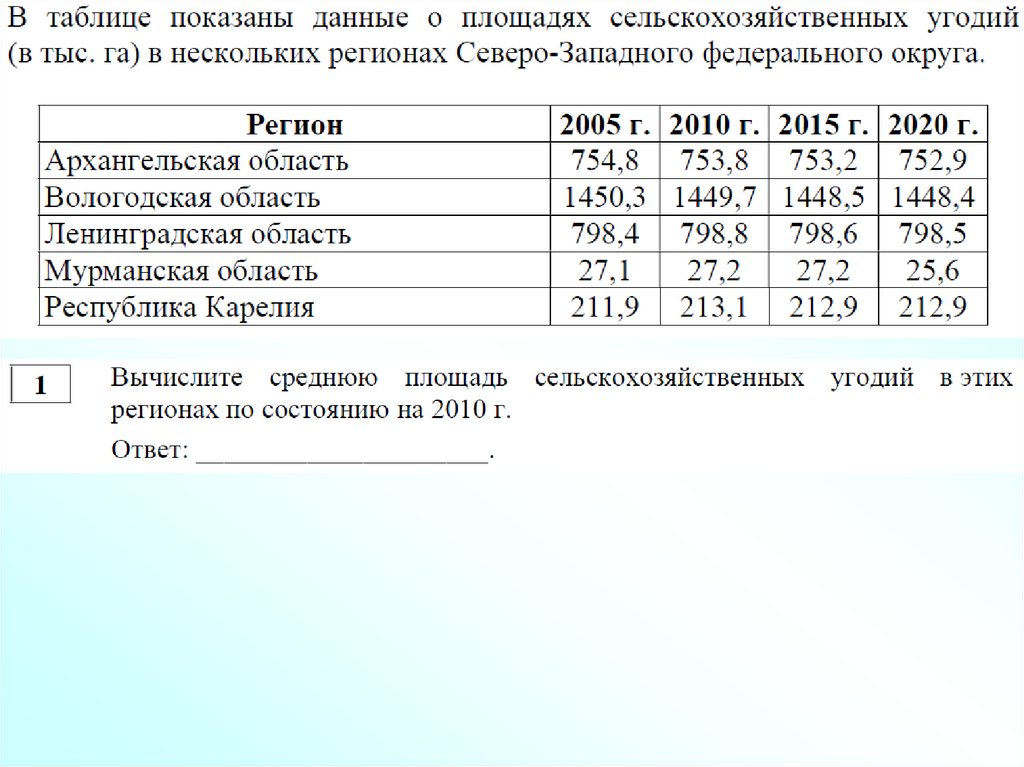
1.

30.03.2024
Классная
р а б о т а.
Подготовка к работе МЦКО.

2.

3.

Среднее арифметическое набора чисел
равно отношению суммы чисел к их
количеству.

4.

648,52
753,8+1449,7 +798,8+27,2+213,1
= 648,52
5

5.

6.

Правило нахождения медианы числового
массива
1. Упорядочить массив по возрастанию.
Получится вариационный ряд.
2. Если в массиве нечётное количество чисел, то медианой является число, стоящее
посередине вариационного ряда.
3. Если в массиве чётное количество чисел,
то медианой обычно считают среднее
арифметическое двух чисел, стоящих
посередине вариационного ряда.

7.

Архангельская область
25,6; 212,9; 752,9; 798,5; 1448,4

8.

9.

0,375
ЧВИ: n = 8
ЧБИ: m = 3
m 3
P ( A) =
= =
n 8
= 0,375
1 бр-к
2 бр-к
3 бр-к
О
О
О
О
Р
Р
Р
Р
О
О
Р
Р
О
О
Р
Р
О
Р
О
Р
О
Р
О
Р
8 исходов

10.

0,25
Число всех исходов: n = 16
Число благоприятных исходов: m = 4
m
4 1
P ( A) =
=
= = 0,25
n 16 4

11.

В С А

12.

13.

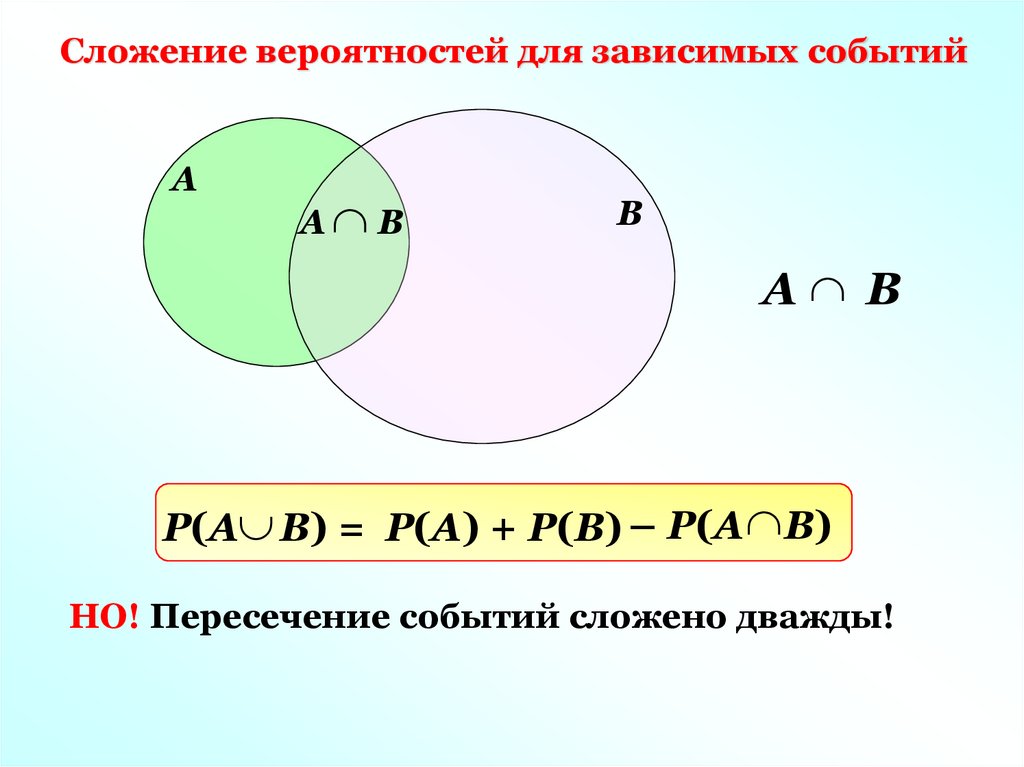
Сложение вероятностей для зависимых событий
А
А В
В
А В
Р(А В) = Р(А) + Р(В) – Р(А В)
НО! Пересечение событий сложено дважды!

14.

0,38
Р(С D) = Р(C) + Р(D) – Р(C D)
0,91 = 0,72 + 0,57 – Р
Р = 0,72 + 0,57 – 0,91
Р = 0,38

15.

16.

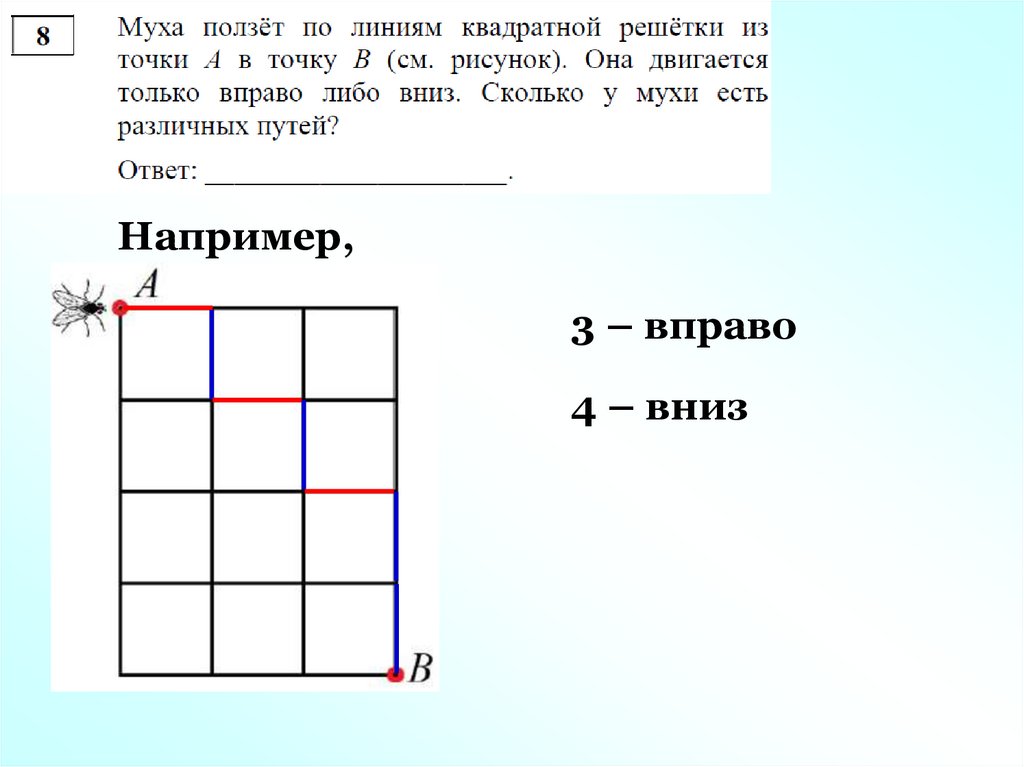
Например,
3 – вправо
4 – вниз

17.

Неупорядоченная выборка:
n!
C =
k!(n k )!
k
n
число сочетаний из n по k

18.

35
3 – вправо
4 – вниз
n!
C =
k!(n k )!
k
n
7!
7 6 5 4!
=
= 35
C =
3! 4!
3 2 4!
3
7

19.

20.

В коробке три красных и три синих карандаша.
Карандаши вытаскиваются по очереди в случайном
порядке. Какова вероятность того, что первый раз
синий карандаш достанут третьим по счёту?
3 1
Р1 =
=
6 2
2
Р2 =
5
3
Р3 =
4
и
и
1 2 3
3
Р= =
= 0,15
2 5 4 20
0, 1 5
3
10 х
х

21.

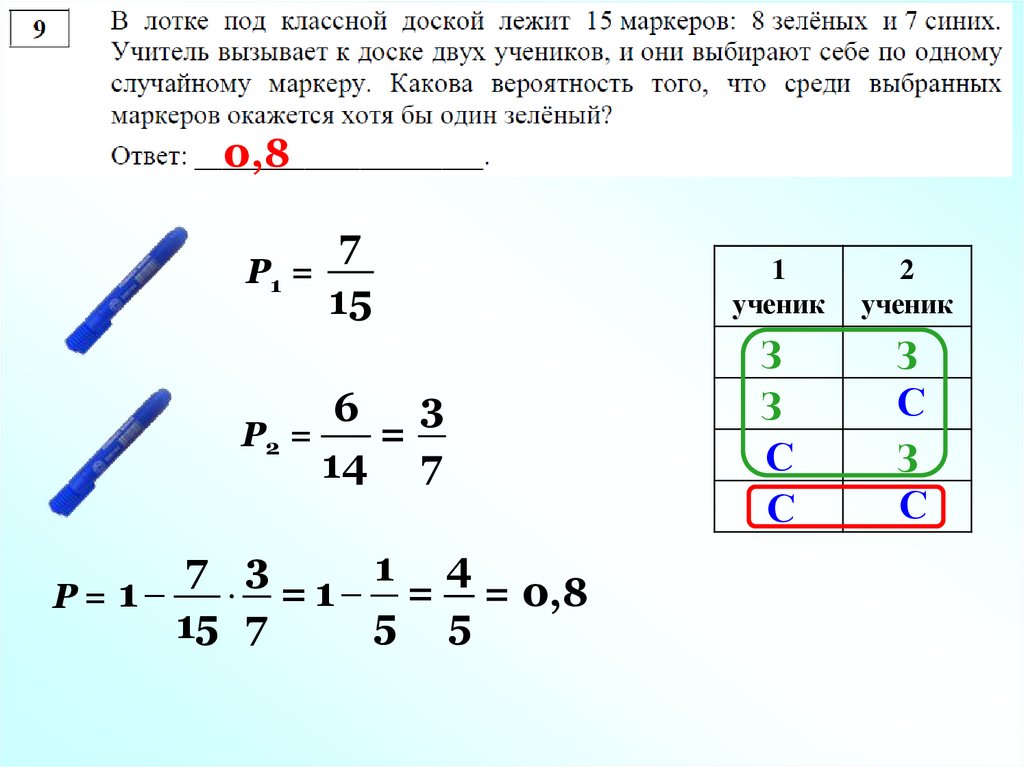
0,8
7
Р1 =
15
3
6
Р2 =
=
14 7
1 4
7 3
= 1 = = 0,8
Р= 1
5 5
15 7
1
ученик
2
ученик
З
З
С
С
З
С
З
С

22.

0,605
3,14
πх 2
=
= 2 =
Р=
Sтр 3х 3 3 1,73
Sкр
2х
30о
х
х 3
1
Sтр = 3 х 2 х 3
2
≈ 0,605

23.

24.

Пусть задан набор точек, причём некоторые
из них могут быть соединены линиями.
Такая система точек и линий называется
графом. Точки называются вершинами, а
линии называются рёбрами. Если две
вершины соединены ребром, их называют
смежными.

25.

Рассмотрим в графе пути, которые начинаются и
Путь, у которого первая и последняя вершины
заканчиваются в одной вершине. Такие пути в
совпадают, а промежуточные вершины не
графе называются циклами. Пройдя по циклу, мы
повторяются, называется циклом.
замыкаем путешествие, возвращаясь в исходную
точку.
В–Р+Г=1
В–Р+Г=2
Например, на рисунке циклами являются пути:
1-2-3-4-5-6-1, 1-2-3-6-1, 3-4-5-3, 3-4-5-6-3.
Не являются циклами: 1-2-3-4-5-3-6-1, 1-2-1

26.

3
В–Р+Г=1
8 – 10 + Г = 1
Г=3

27.

28.

n!
C =
k!(n k )!
k
n
0,276
n=6
р = 0,4
k=3
q = 0,6
6 4 3!
6!
3
3
3
0,24 = 0,276
Р=
0,4 0,6 =
2 3!
3! 3!