Похожие презентации:
Демо - версия МЦКО
1.
Демо-версия МЦКО2.
№ 1 Укажите при каких значениях a выражение 5a + 9принимает только отрицательные значения?
5a + 9 < 0
5a < – 9 : 5
9
а<
5
Ответ:
9
1) а >
5
5
2) а <
9
5
3) а >
9
9
4) а <
5
Ответ: 4
3.
2№ 2 Найдите значение выражения 4,5
1
1
9 1,4 9 .
1 1
1 1
1
4,5 1,4 = 4,5 1,4 =
9 9
9 9
9
0,5
1
1 4,5 1
1
=
1,4 = 0,5 1,4 = 0,9 =
9
9 1 9
9
1
0,1
1 0,9
=
= – 0,1
9 1
1
Ответ: – 0,1
4.
№ 3 Решите уравнение х2 – 16 = 6х. Если уравнение имеет болееодного корня, в ответе укажите меньший из них.
х2 – 16 = 6х
х2 – 6х – 16 = 0
а=1
b=–6
с = – 16
–b=6
D = b2 – 4ac = (– 6)2 – 4·1·(– 16) = 36 + 64 = 100
6+ 100 16
b + D
х1 =
=
=
=8
2a
2
2
6 100 4
b D
=
=
х2 =
=– 2
2a
2
2
Ответ: – 2
5.
№4В магазине канцтоваров продаётся 200 ручек: 31 красная,
25 зелёных, 38 фиолетовых, остальные синие и чёрные, их
поровну. Найдите вероятность того, что случайно выбранная
в этом магазине ручка будет красной или чёрной.
ЧВИ: n = 200
200 – (31 + 25 + 38) = 106 синих и чёрных
106 : 2 = 53 чёрных
ЧБИ: m = 31 + 53 = 84
84
42
m
=
= 0,42
P ( A) =
=
n 200 100
Ответ: 0,42
6.
Формула сложных процентовВклад в банк составляет а р.
р% годовых
Срок хранения вклада t лет
Снимают все деньги в конце срока.
p
а 1+
100
t
7.
№ 5 В феврале цена на товар снизилась на 15%. В марте цена натовар повысилась на 10% и стала равной 1309 рублям.
Сколько рублей стоил товар в январе?
а р. – первоначальная цена товара
15
10
а 1
= 1309
1+
100
100
3
1
а 1
1+
= 1309
20
10
17 11
а
= 1309
20 10
а = 1309
20 10
17 11
а = 7 · 20 · 10
а = 1400
Ответ: 1400
8.
№ 6 Найдите значение выражения(am)n = amn
an ∙ am = an+m
(0,48 )4 0,412 0,432 0,412 0,4 44
=
=
=
45
45
45
0,4
0,4
0,4
1
1
4
10
–
1
=
= 0,444 – 45 = 0,4 =
=
10
4
5
= = 2,5
2
Ответ: 2,5
9.
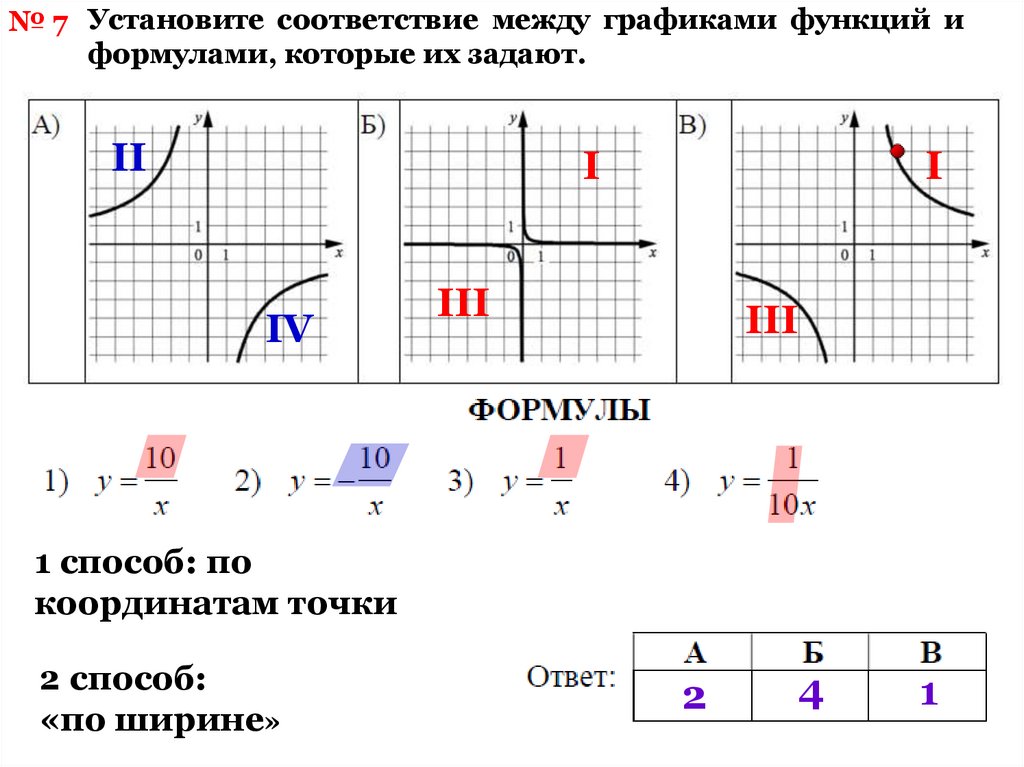
№ 7 Установите соответствие между графиками функций иформулами, которые их задают.
II
I
IV
I
III
III
1 способ: по
координатам точки
2 способ:
«по ширине»
2
4
1
10.
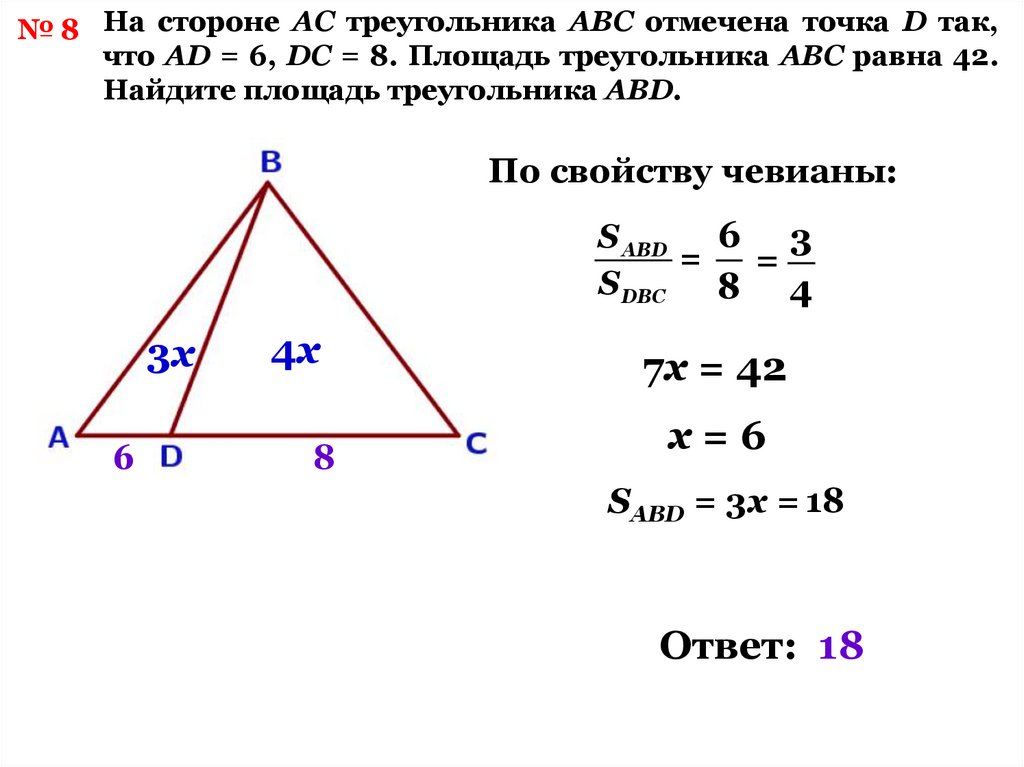
№ 8 На стороне АС треугольника АВС отмечена точка D так,что АD = 6, DC = 8. Площадь треугольника АВС равна 42.
Найдите площадь треугольника АВD.
По свойству чевианы:
6 3
S АВD
=
=
S DВС
8 4
3х
6
4х
8
7х = 42
х=6
SАВD = 3х = 18
Ответ: 18
11.
№ 9 Около окружности описана трапеция, периметр которойравен 24. Найдите длину её средней линии.
сумма 12
АВ + СD = АD + ВС =
сумма 12
= РАВСD : 2
Средняя линия равна полусумме оснований
Ответ: 6
12.
№ 10В прямоугольном треугольнике
медиана, проведённая из вершины прямого угла, равна половине гипотенузы.
Ответ: 3
13.
№ 11vсоб = х км/ч
по
течению
против
течения
28
t1 + t2 = 9
60
vтеч = 3 км/ч
v, км/ч
t, ч
s, км
х+3
48
х +3
48
х–3
48
х 3
48
48
48
8
+
=8
х +3 х 3
15
14.
4848
8 15+8
+
=
:8
х +3 х 3
15
6
6
15+1
+
=
:2
х +3 х 3
15
х–3
х+3
3
3
8
+
=
х +3 х 3 15
3 х 9+3 х + 9 8
=
2
х 9
15
6х
8
=
:2
2
х 9 15
3х
4
=
2
х 9 15
15.
3х4
=
2
х 9 15
4х2 – 36 = 45х
ОДЗ: х2 – 9 ≠ 0
х2 ≠ – 3
х1 ≠ 3
4х2 – 45х – 36 = 0
1 способ
D = b2 – 4ac = 452 + 16 · 36 = 45 · 45 + 16 · 36 =
= 9 · (5 · 45 + 16 · 4) = 9 · 289
b + D 45+ 9 289 45+ 3 17
= 12
=
=
х1 =
2a
8
8
х2 < 0 (не подходит по смыслу)
Ответ: 12 км/ч
16.
4х2 – 45х – 36 = 02 способ
4х2 – 48х + 3х – 36 = 0
4х(х – 12) + 3(х – 12) = 0
(х – 12)(4х + 3) = 0
х1 = 12
х2 < 0 (не подходит по смыслу)
Ответ: 12 км/ч
17.
№ 129
12
Дано: АBCD – трапеция,
АF и ВF – биссектрисы,
АF = 12, ВF = 9
Найти: АВ
Решение.
1) Сумма углов, прилежащих к боковой стороне
трапеции, равна 180о, значит, AВF + ВAF =
1
1
1
1
= AВC + ВAD = ( AВC + ВAD) = 180о = 900
2
2
2
2
2) AFВ = 180о – 90о = 90о.
3) Найдём АВ из ΔАВF по т. Пифагора:
18.
№ 129
12
Дано: АBCD – трапеция,
АF и ВF – биссектрисы,
АF = 12, ВF = 9
Найти: АВ
Решение.
3) Найдём АВ из ΔАВF по т. Пифагора:
АВ = 92 + 122 = 15
Ответ: 15
















 Математика
Математика








