Похожие презентации:
Хранение данных в ЭВМ
1.
Раздел 3. Хранение данных вЭВМ.
1. Классификация объектов,
2. Простые типы данных
2.
Характеристики объектов в ОЗУЛогические характеристики
Физические характеристики
Имя
Адрес в ОЗУ
Состояние
Значение
Тип
Внутренний формат (схема битов);
Единый набор операций;
Диапазон допустимых значений.
Область видимости
Область видимости
Архитектура вычислительных систем
3.
Классификация объектов в ОЗУОбъекты в ОЗУ
простые
сложные
многовариантные
Целые числа
массивы
вариантный тип
вещественные
числа
строки
объединение
символы
записи
логические
объекты
классы
Архитектура вычислительных систем
4.
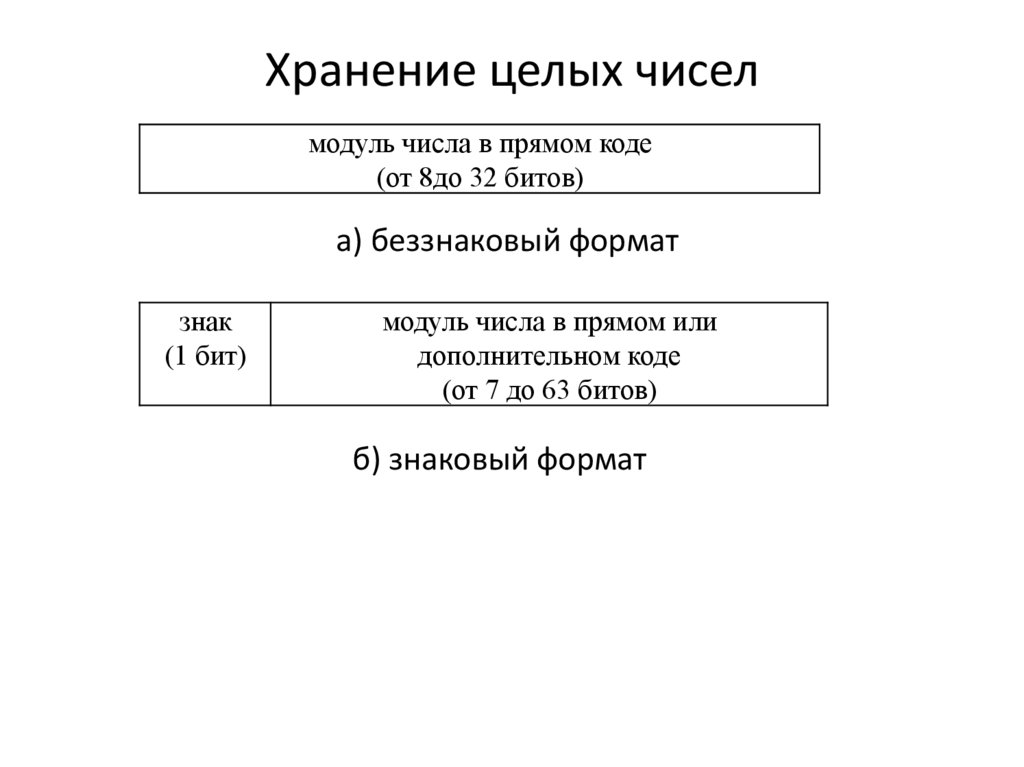
Хранение целых чиселмодуль числа в прямом коде
(от 8до 32 битов)
а) беззнаковый формат
знак
(1 бит)
модуль числа в прямом или
дополнительном коде
(от 7 до 63 битов)
б) знаковый формат
5.
Целочисленные 32-разрядные типыданных
Способ
хранения
данных
знаковый
Обозначение
типа
Диапазон значений
Длина
(байт)
Integer
-2147483648 …2147483647
4
ShortInt
SmallInt
LongInt
-128 …127
-32768 …32767
-2147483648 …2147483647
1
2
4
-263 …263 - 1
0 …4294967295
0 …255
0 …65535
0 …4294967295
8
4
1
2
4
Int64
беззнаковый Cardinal
Byte
Word
LongWord
6.
Хранение вещественных чисел1. Используется экспоненциальная форма
представления с нормализованной мантиссой:
y = m * pk
Здесь m – мантисса, p – основание СС, k – порядок.
1≤m<p
2. Вместо порядка, который может быть как
положительным, так и отрицательным, хранится
экспонента:
e = k + const
3. Хранится только дробная часть нормализованной
мантиссы.
4. Используется только прямой двоичный код.
5. Пример внутреннего формата вещественного числа:
s (1 бит)
e (8 битов)
f (23 бита)
7.
Погрешность хранения вещественных чисел1. Вещественные числа хранятся с ограниченной точностью.
2. Мерой точности является погрешность, которая может быть
абсолютной и относительной. Абсолютная погрешность равна
∆ = y0 – yвн ,
где y0 - истинное значение числа, yвн – значение числа, представленного во внутреннем формате.
3. Относительная погрешность определяется следующим образом:
δ = ∆ / y0 * 100 (%).
Правила вычислений с вещественными числами:
Умножение (a Деление (a / b)
Сложение (a + b)
* b)
m1 * pk1 m2 * pk2 m1 * m2* p(k1+k2) (m1 / m2)* p(k1-k2) m3 * pk3
где k3 = max{ k1, k2},
m3 - значение мантиссы, приведенное к
наибольшему порядку
a
b
8.
Причины снижения быстродействияпри работе с вещественными числами
1. Затраты времени при переводе во внутренний формат (нормализация мантиссы,
расчет экспоненты).
2. Выполнение всех действий проводится над
двумя числами (мантисса, порядок).
3. Приведение порядков при сложении чисел.
9.
Вещественные типы данныхОбозначение типа
Single
Real48
Real
Double
Extended
Comp
Диапазон
значений
1,5*10-45
…3,4*1038
2,9*10-39
…1,7*1038
5*10-324
…1,7*10308
5*10-324
…1,7*10308
3,6*10-4951
…1,1*104932
-263 + 1…263 -1
Общая Длина Длина Констан- Поля
длина
e
f
та
(байт) (бит)
(бит)
4
8
23
127
sef
6
8
39
129
sfe
8
11
52
1023
sef
8
11
52
1023
sef
10
15
63
16383
sef
8
-
-
-
sd
10.
Особенности хранения некоторыхвещественных типов данных
1.Тип Extended (10 байтов) - хранит нормализованную мантиссу полностью (целая часть хранится в
третьем поле, дробная – в четвертом)
s (1 бит) e (15 битов)
1
f (63 бита)
2.Тип Comp (8 байтов) - является целочисленным
знаковым форматом, но не относится к перечисляемым типам данных; при вводе в него вещественного числа дробная часть отбрасывается.
s (1 бит)
d (63 бита)
11.
Пример перевода во внутренний формат SingleЗаписать число 6,45 во внутреннем формате Single. Двоичное представление записать с точностью 5 разрядов после запятой.
Решение.
а) переводим число в двоичную систему и определяем дробную часть
нормализованной мантиссы: 6,45 = 110, 011102 = 1,1001110 * 22;
f = 1001110;
б) находим экспоненту: e = 2 + 127 = 129 = 100000012;
в) находим значение знакового разряда: s = 0, т.к. число положительное.
г) записываем внутренний формат:
0
10000001
10011100000000000000000
д) находим десятичное значение представляемого числа:
110,011102 = 6,4375;
е) находим абсолютную погрешность представления:
∆=6,45 - 6,4375=0,0125;
ж) находим относительную погрешность представления:
δ = 0,0125 * 100 / 6,45 =0,194 %
12.
Хранение символов1. Символы (литеры) хранятся в виде целых беззнаковых
чисел, которые называются кодами.
2. Для формирования символьного кода используются
кодировочные таблицы ASCII , ANSI, UNICODE, KOI-8 и т.д.
3. Первые 128 кодов символов во всех таблицах являются стандартными для всех видов ЭВМ
Основные характеристики
кодировочных таблиц
Объем памяти для хранения
одного символа, байт
Максимальное число
символов
Коды символов кириллицы
Номер кодировочной
таблицы для России
ASCII
ANSI
UNICODE
1
1
2
256
256
65536
128 – 175, 224 - 239
866
192-255
1251
1040 - 1103
отсутствует
13.
Примеры подмножества таблицы ASCIIКод
32
33
34
35
36
37
38
39
40
41
42
43
44
45
20
30
40
50
60
70
0
<SP
>
0
@
P
`
p
Символ
пробел
!
“
#
$
%
&
'
(
)
*
+
,
-
Код
46
47
48
49
50
51
52
53
54
55
56
57
58
59
Символ
.
/
0
1
2
3
4
5
6
7
8
9
:
;
Код
60
61
62
63
64
65
66
67
68
69
70
71
72
73
Символ
<
=
>
?
@
A
B
C
D
E
F
G
H
I
1
2
3
4
5
6
7
8
9
A
B
C
D
E
F
!
1
A
Q
a
q
"
2
B
R
b
r
#
3
C
S
c
s
$
4
D
T
d
t
%
5
E
U
e
u
&
6
F
V
f
v
'
7
G
W
g
w
(
8
H
X
h
x
)
9
I
Y
i
y
*
:
J
Z
j
z
+
;
K
[
k
{
,
<
L
\
l
|
=
M
]
m
}
.
>
N
^
n
~
/
?
O
_
o
14.
Символьные типы данныхОбозначение
типа
Char
AnsiChar
WideChar
Размер (байт)
Кодировка
1
1
2
ASCII
ANSI
UNICODE
Допустимые операции:
1. Сравнение (сравниваются коды символов, т.е. ‘‘A’’ < ‘‘B’’)
2. Символьные типы относятся к порядковым типам, т.е.
возможно применять следующие функции:
Succ - возвращает следующий символ литерного множества;
Pred - возвращает предыдущий символ литерного множества;
Ord - возвращает значение кода символа;
Chr - возвращает значение символа по его коду.
15.
Хранение логических данных1. Логические объекты могут принимать только два
значения – TRUE и FALSE (ИСТИНА или ЛОЖЬ, 1
или 0).
2. Для хранения логического объекта достаточно
одного бита, но реально в памяти выделяется 1
байт, как минимально адресуемая единица.
3. В языках программирования для описания
логических объектов используется тип Boolean.
4. Допускается выполнение множества логических
операций (отрицание, конъюнкция, дизъюнкция и
т.д.)














 Программирование
Программирование








