Квадратичная функция

1.

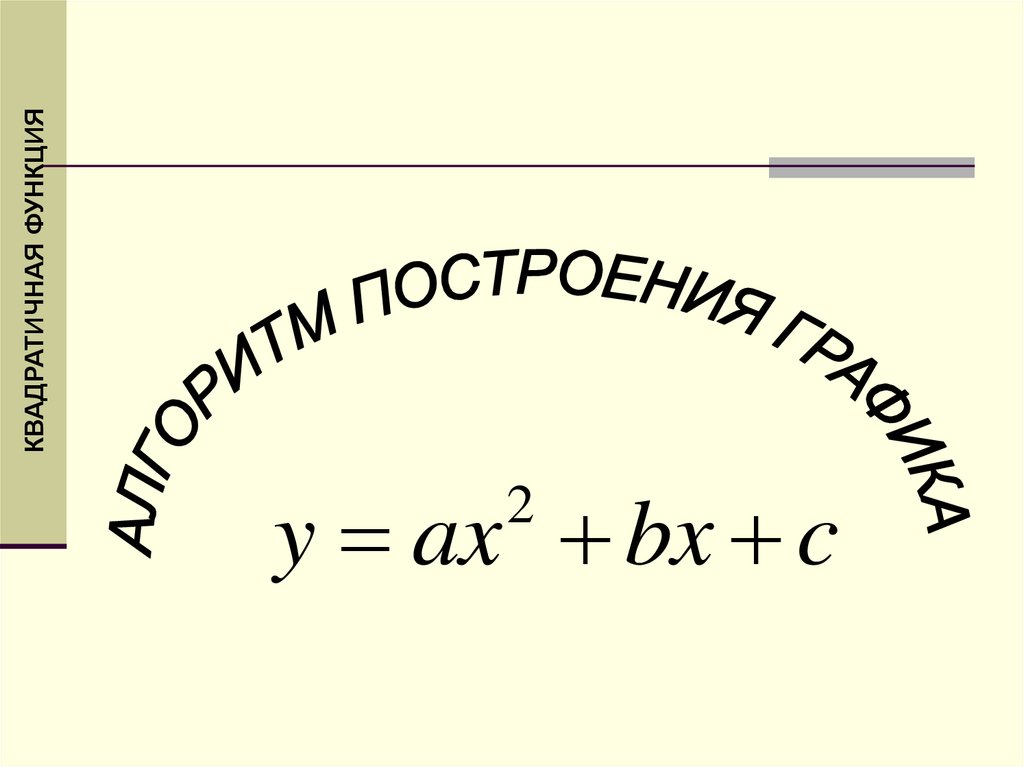
y = ax2 + bx + c

2.

Оглавление:
Понятие функции.
Способы задания функции.
Квадратичная функция:
а) определение;
б) алгоритм построения;
в) исследование функции.
Практические задания.
Верные решения.
Вариант 1;
Вариант 2.
Проверь себя:
Вариант 1;
Вариант 2.
Выход.

3.

ПОНЯТИЕ ФУНКЦИИ.
Если на заданном множестве каждому
значению х поставлено в соответствии по
заданному правилу значение у, то говорят,
что на данном множестве задана функция.
Х – независимая переменная ( аргумент)
У – зависимая переменная ( функция)

4.

Способы задания функции
Аналитический способ
у 2х 1
y 3x 1
y x 1
2
y
x
2

5.

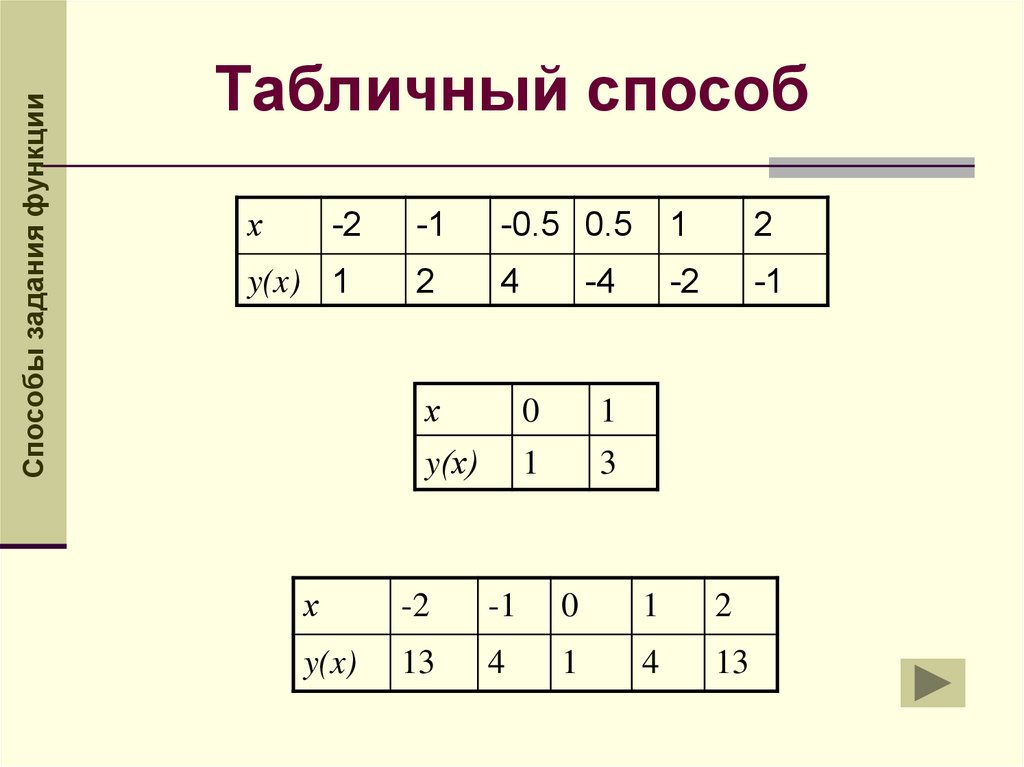
Способы задания функции
Табличный способ
х
-2
-1
-0.5 0.5
1
2
y(x) 1
2
4
-2
-1
-4
х
0
1
y(х)
1
3
х
-2
-1
0
1
2
y(x)
13
4
1
4
13

6.

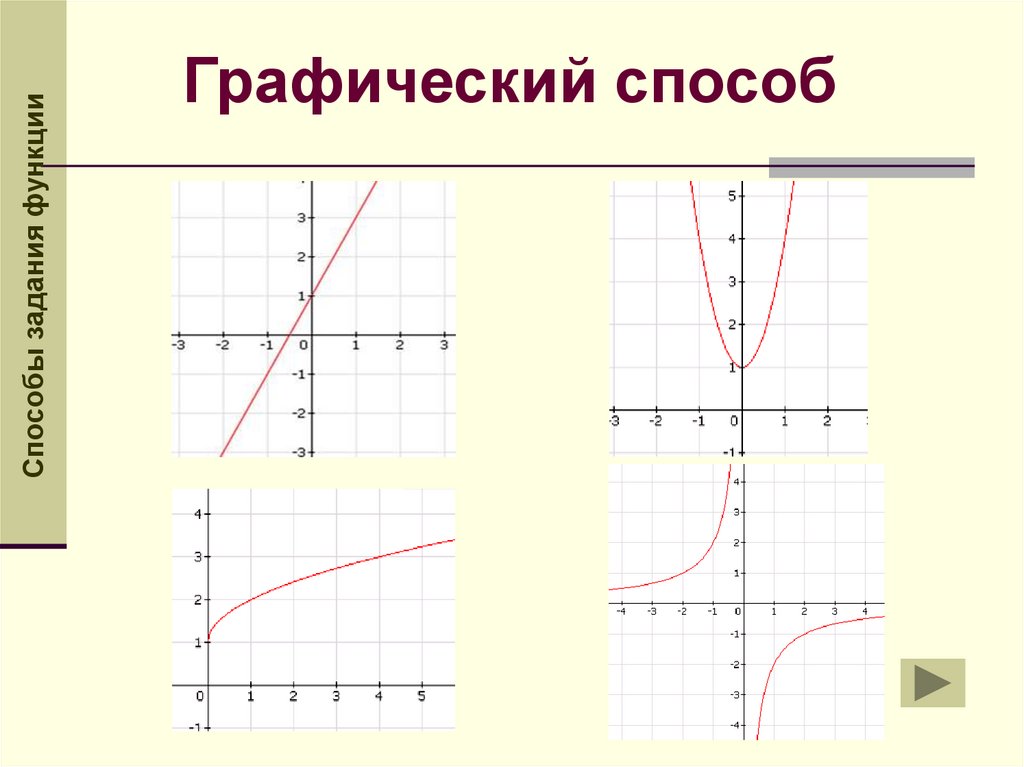
Способы задания функции
Графический способ

7.

Способы задания функции
Коротко о главном
у 2х 1
1. Формула
2. Таблица
3. График
х
0
1
У(х)
1
3

8.

КВАДРАТИЧНАЯ ФУНКЦИЯ
ОПРЕДЕЛЕНИЕ
Функция у=ах2+bx+с, где а,b и с
заданные действительные числа, а≠0,
х - независимая переменная,
называется квадратичной функцией.
Например: у=х2,
у=3х2+5,
у=-4х2-6х+1

9.

y ax bx c
2
КВАДРАТИЧНАЯ ФУНКЦИЯ

10.

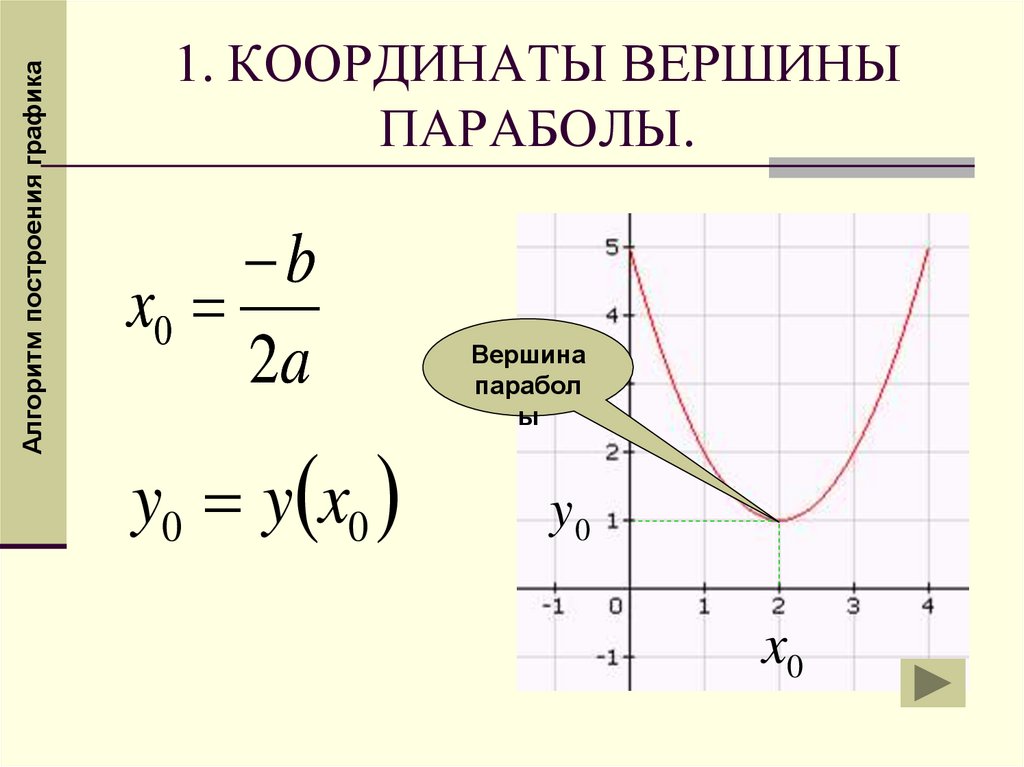
Алгоритм построения графика
1. КООРДИНАТЫ ВЕРШИНЫ
ПАРАБОЛЫ.
b
x0
2a
y0 y x0
Вершина
парабол
ы
y0
x0

11.

Алгоритм построения графика
Пример №1
y x 4x 3
2
a=1, b=-4.
4
x0 2
2
y0 y 2 2 4 2 3 1
2
(2; -1) координаты вершины параболы

12.

Алгоритм построения графика
Пример №2
y 2x 4
2
a=2, b=0.
0
x0 0
4
y0 y 0 2 0 4 4
2
(0;4) координаты вершины параболы

13.

Алгоритм построения графика
2. НАПРАВЛЕНИЕ ВЕТВЕЙ
ПАРАБОЛЫ.
1.Если а>0, то ветви
параболы направлены
вверх.
а<0
а>0
2. Если а<0, то ветви
параболы направлены
вниз.

14.

Алгоритм построения графика
Например:
y 3x 2 x 4
2
2 2
y x 4
3
a=3,
a>0 => ветви параболы
направлены вверх
2
a= ,
3
a<0 => ветви параболы
направлены вниз

15.

Алгоритм построения графика
Например:
y 3x 4 x
2
x
y
2
2
a=-4,
a<0 => ветви параболы
направлены вниз
1
a= 2 ,
a>0 => ветви параболы
направлены вверх

16.

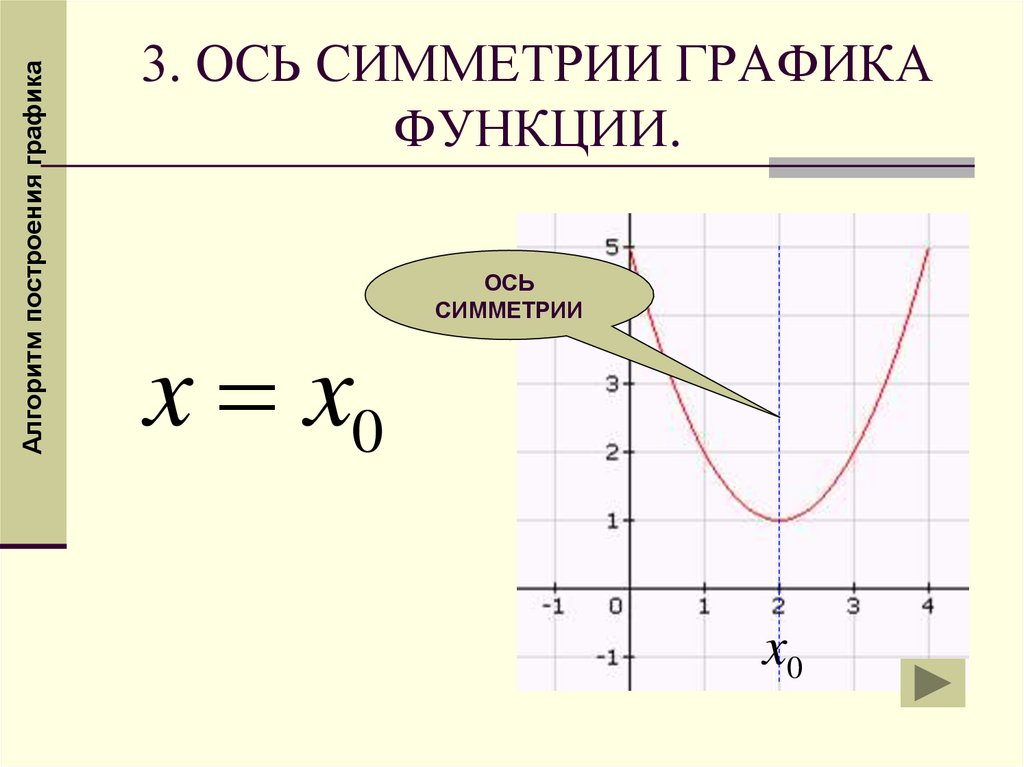
Алгоритм построения графика
3. ОСЬ СИММЕТРИИ ГРАФИКА
ФУНКЦИИ.
x x0
ОСЬ
СИММЕТРИИ
x0

17.

Алгоритм построения графика
Например:
y x 4x 3
2
Координаты вершины параболы (2;-1) т.е.
x0=2 значит ось симметрии параболы – прямая x=2
y 2x 4
2
Координаты вершины параболы (0;-4) т.е.
x0=0 значит ось симметрии параболы – прямая x=0
(совпадает с осью ОY)

18.

Алгоритм построения графика
4. ОФОРМЛЕНИЕ ТАБЛИЦЫ.
Составляем таблицу для значений х, взятых по
одну сторону от оси симметрии.
Например: у(х)=х2-2х+3 , т.к. ось симметрии х=1 ,
то берем значения х>1 или х<1.
x 2
х 3
х 4
х
y(x)
у(2) 22 2 2 3 3
у(3) 32 2 3 3 6
у(4) 42 2 4 3 11
2 3 4 5 6
3 6 11 18 27

19.

Пример
Построение графика квадратичной
функции.
у х 2x 4
2

20.

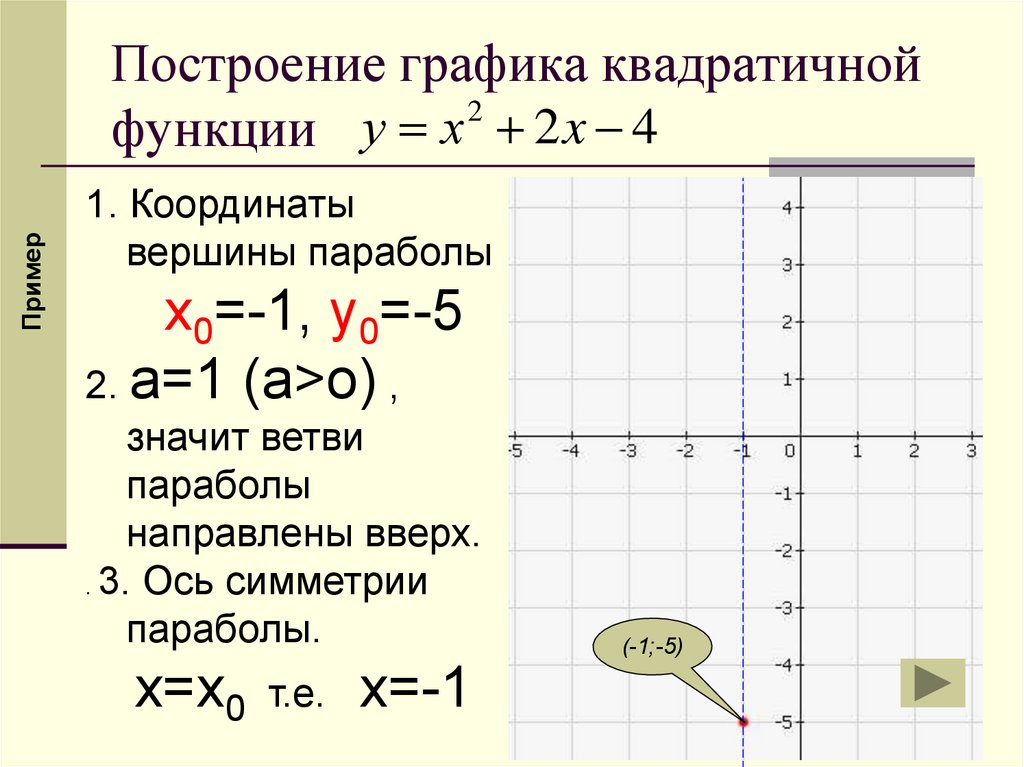
Пример
Построение графика квадратичной
2
функции у х 2 x 4
1. Координаты
вершины параболы
х0=-1, у0=-5
2. а=1 (а>o) ,
значит ветви
параболы
направлены вверх.
. 3. Ось симметрии
параболы.
х=х0 т.е. х=-1
(-1;-5)

21.

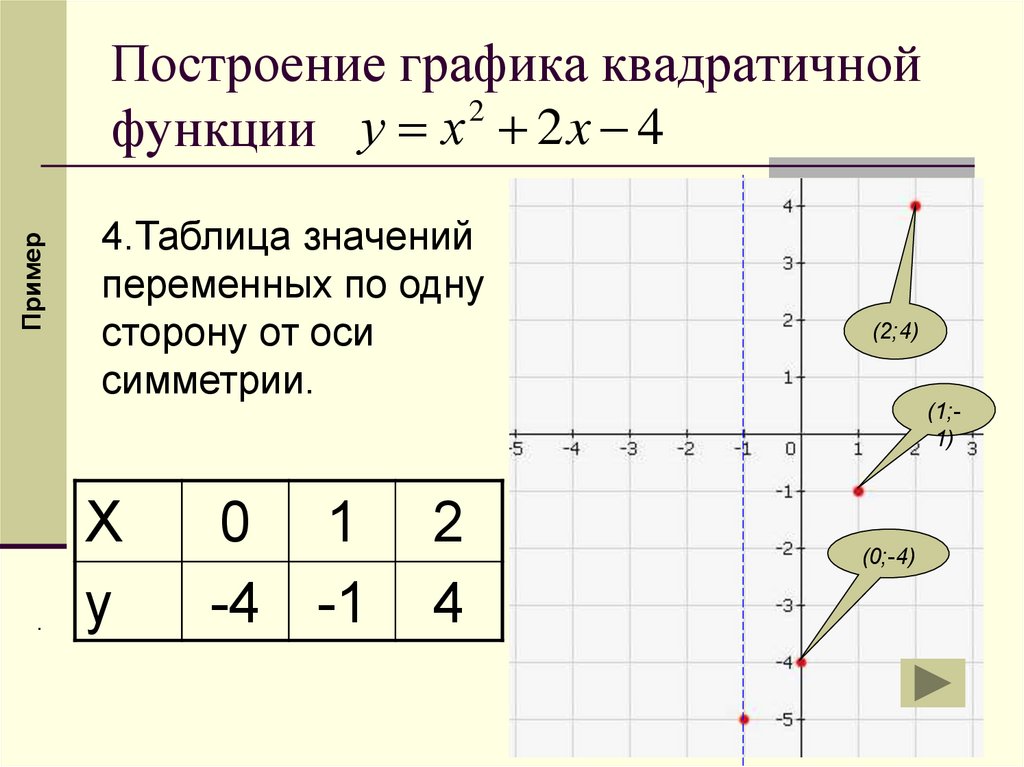
Пример
Построение графика квадратичной
2
функции у х 2 x 4
4.Таблица значений
переменных по одну
сторону от оси
симметрии.
(2;4)
(1;1)
.
Х
у
0 1
-4 -1
2
4
(0;-4)

22.

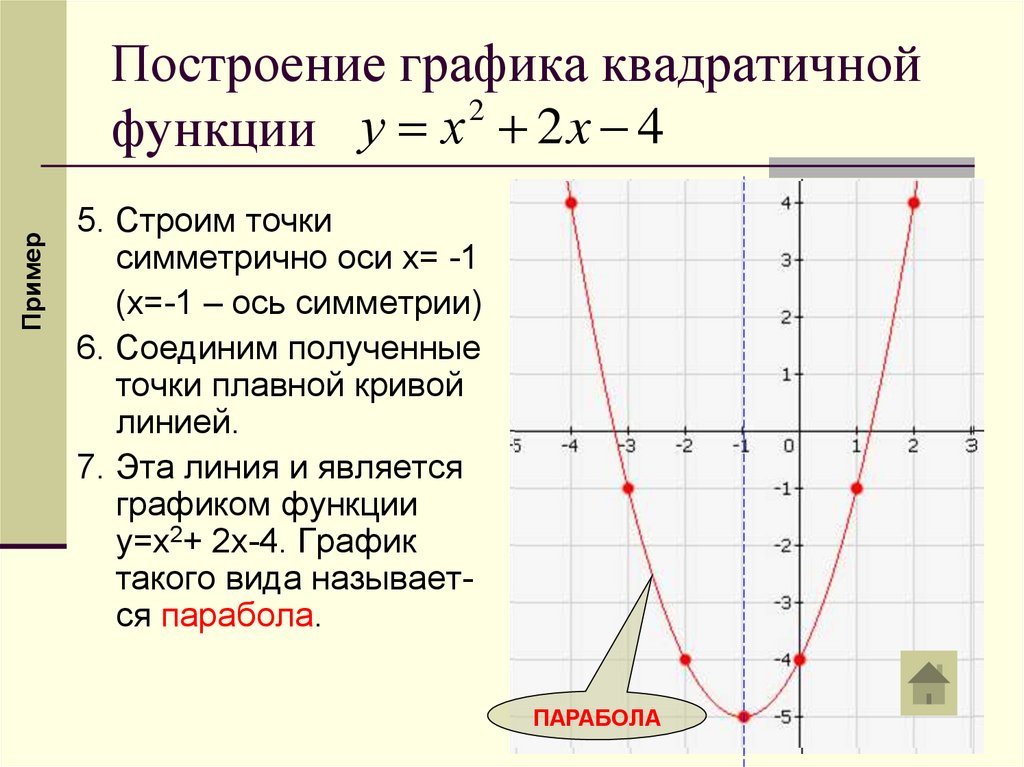
Пример
Построение графика квадратичной
2
функции у х 2 x 4
5. Строим точки
симметрично оси x= -1
(x=-1 – ось симметрии)
6. Соединим полученные
точки плавной кривой
линией.
7. Эта линия и является
графиком функции
y=x2+ 2x-4. График
такого вида называется парабола.
ПАРАБОЛА

23.

Исследование функции y = ax2 + bx + c
Область определения функции.
Область определения функции – это
множество значений х, при которых функция
имеет смысл.
2
,х 0
Например: y
x
y x 1 , х 0
у aх bx c , х R
2

24.

Исследование функции y = ax2 + bx + c
Нули функции.
Значения х, при которых
функция принимает значения
равные нулю, называются
нулями функции.
(Это точки пересечения
графика функции с осью Ох.)
Например: найти нули
функции
2
Нули
функции
y x 4x 5
y=0, x2+4x-5=0 по теореме обратной
теореме Виета x1+x2=-4, x1x2=-5, x1=1,
x2=-5 т.е.
y 0 , при x1 1, x2 5.

25.

Исследование функции y = ax2 + bx + c
Наибольшее или наименьшее
значение функции.
Наибольшее или наименьшее
значение функция у=ax2+bx+c
принимает в точке
x0= - b/2a.
наименьше
е
Если ветви параболы направлены
вверх (а>0), то у0=у(х0) –
наименьшее значение функции.
Если ветви параболы направлены
вниз (а<0), то у0=у(х0) –
наибольшее
наибольшее значение функции.

26.

Например
y x 4x 3
2
а=4, a>0, ветви параболы направлены вверх, значит
можно найти наименьшее значение функции. (-2; -1)
– координаты вершины
yнаименьшее==y(-2)=-1
y 4x x
2
а=-1, a<0, ветви параболы направлены вниз, значит
можно найти наибольшее значение функции. (2; 4) –
координаты вершины
yнаибольшее==y(2)=4

27.

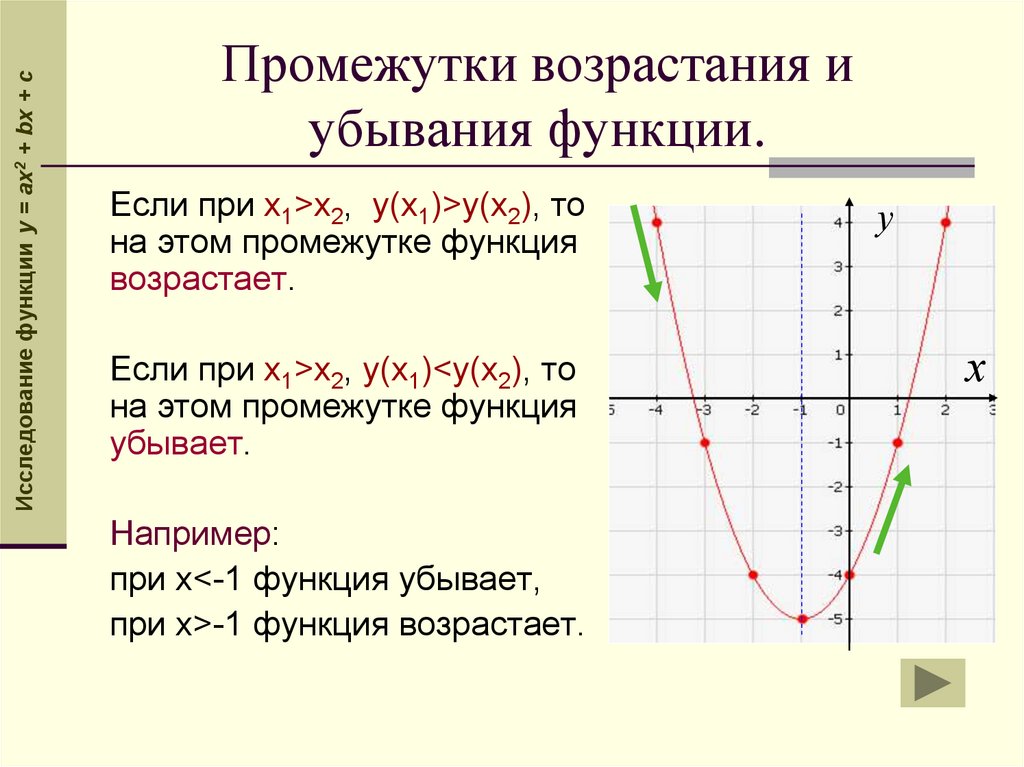
Исследование функции y = ax2 + bx + c
Промежутки возрастания и
убывания функции.
Если при х1>x2, у(х1)>у(х2), то
на этом промежутке функция
возрастает.
Если при х1>х2, у(х1)<у(х2), то
на этом промежутке функция
убывает.
Например:
при х<-1 функция убывает,
при х>-1 функция возрастает.
у
х

28.

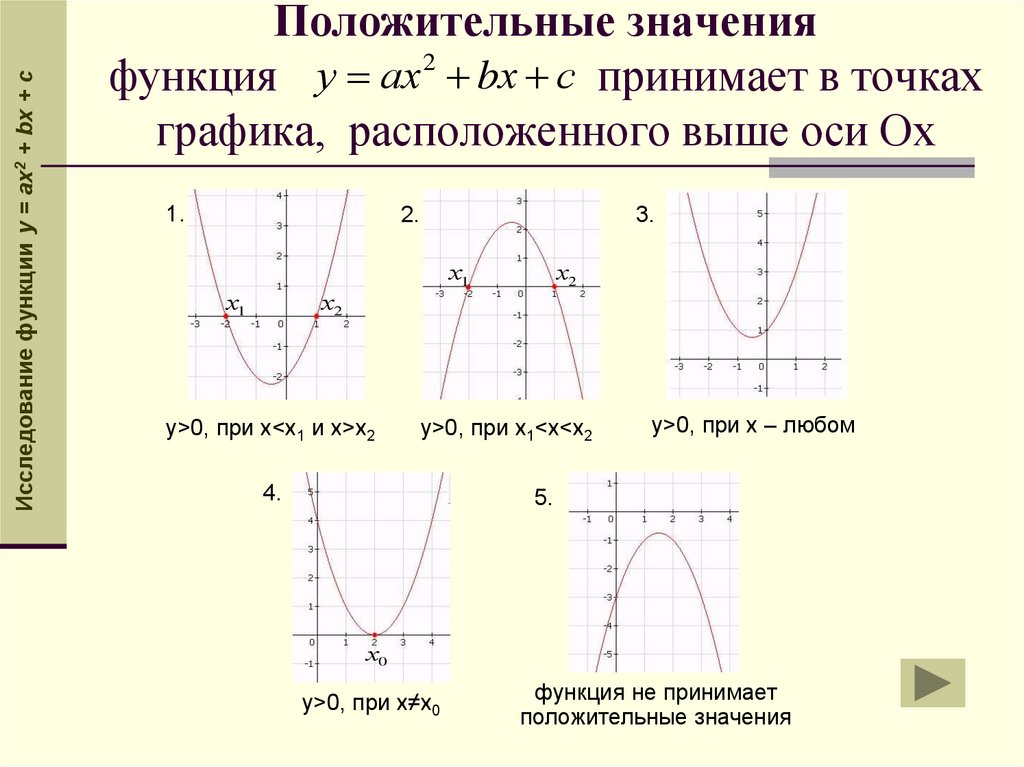
Исследование функции y = ax2 + bx + c
Положительные значения
2
у
ах
bх с принимает в точках
функция
графика, расположенного выше оси Ох
1.
2.
3.
х1
х1
х2
х2
у>0, при х<х1 и х>х2
у>0, при х1<х<х2
4.
у>0, при х – любом
5.
х0
у>0, при х≠х0
функция не принимает
положительные значения

29.

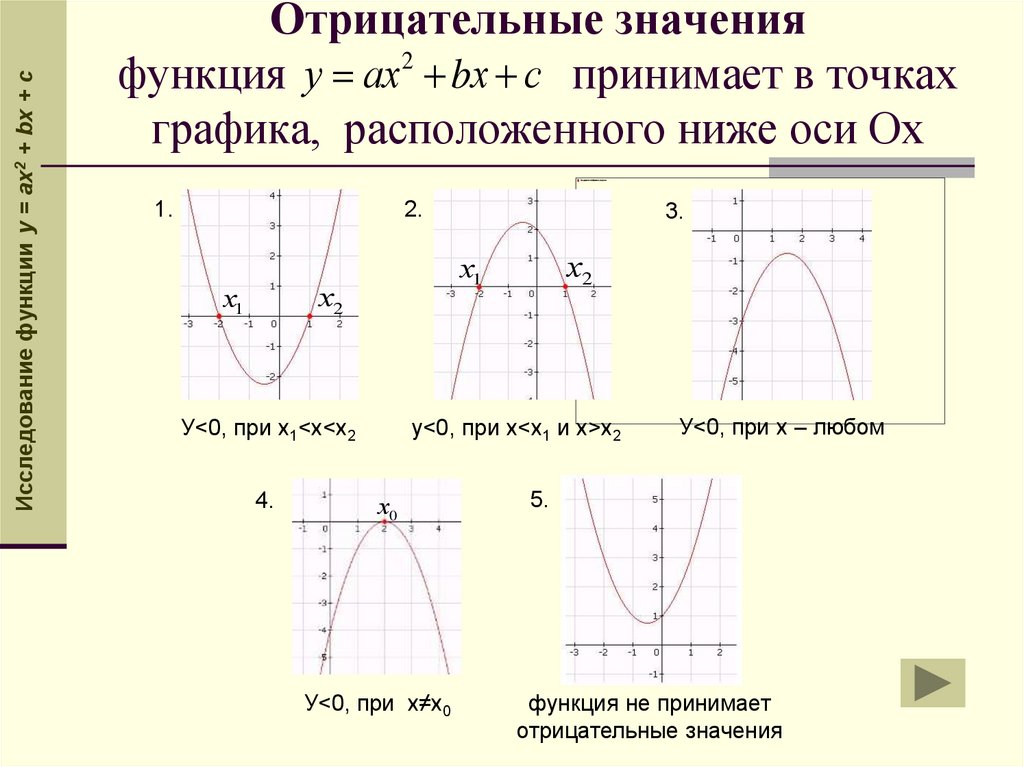
Исследование функции y = ax2 + bx + c
Отрицательные значения
функция у ах 2 bх с принимает в точках
графика, расположенного ниже оси Ох
1.
2.
У<0, при х1<x<х2
4.
х2
х1
х2
х1
3.
у<0, при х<х1 и х>х2
х0
У<0, при х≠х0
У<0, при х – любом
5.
функция не принимает
отрицательные значения

30.

Практические задания
Постройте график квадратичной функции и
исследуйте её.
Вариант 1.
Вариант 2.
у = -х2-2х+3
у = х2+2х-3

31.

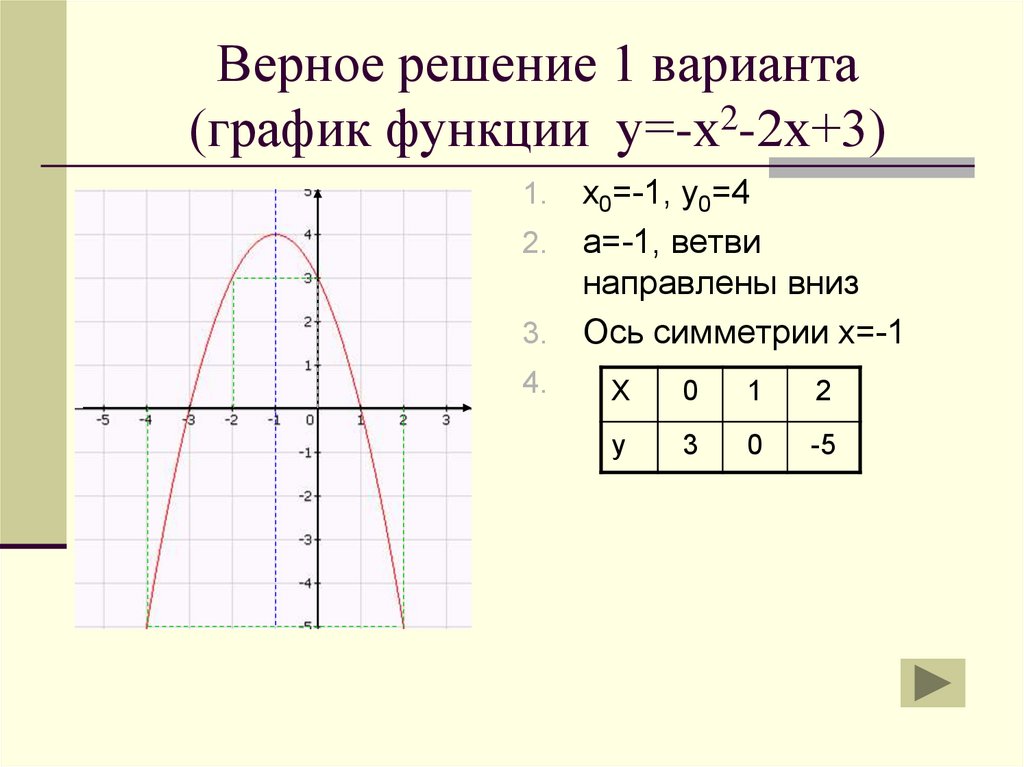
Верное решение 1 варианта
(график функции у=-х2-2х+3)
х0=-1, у0=4
2. а=-1, ветви
направлены вниз
3. Ось симметрии х=-1
1.
4.
Х
0
1
2
у
3
0
-5

32.

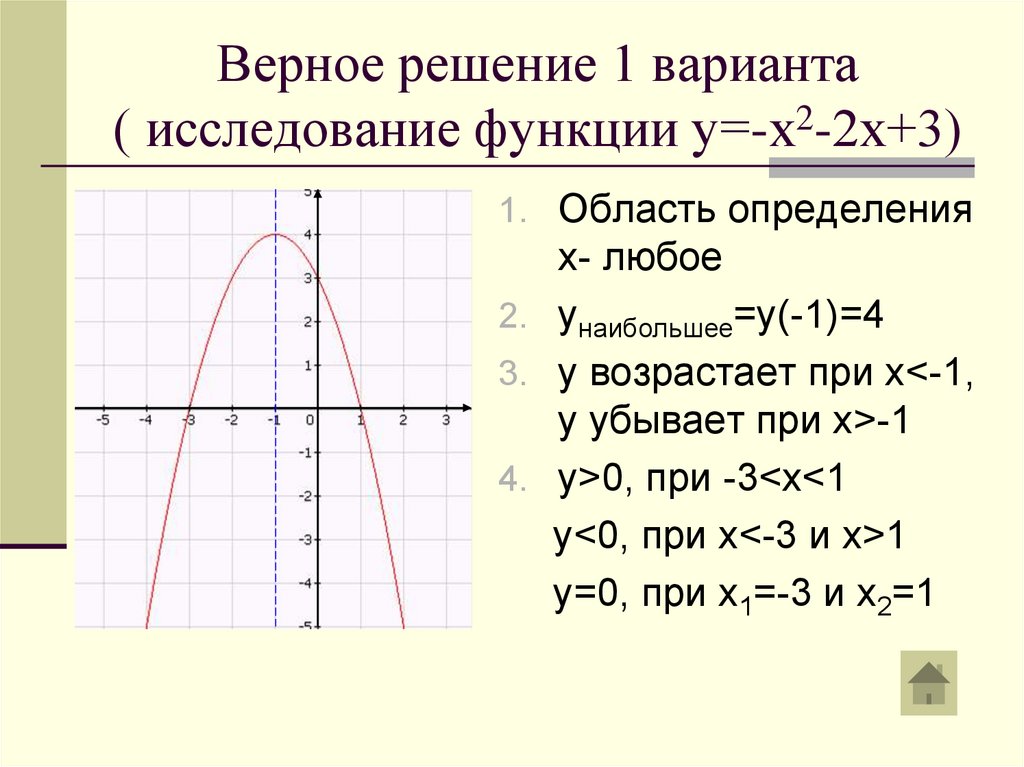
Верное решение 1 варианта
( исследование функции у=-х2-2х+3)
1. Область определения
х- любое
2. унаибольшее=у(-1)=4
3. у возрастает при х<-1,
у убывает при х>-1
4. у>0, при -3<x<1
у<0, при х<-3 и х>1
у=0, при х1=-3 и х2=1

33.

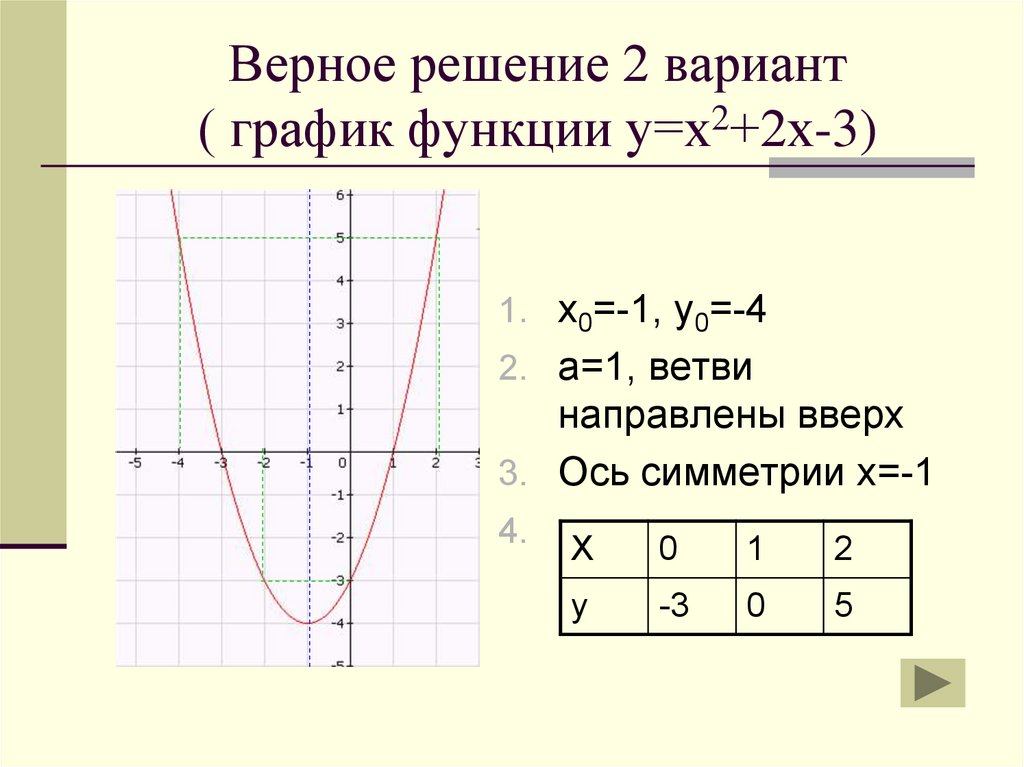
Верное решение 2 вариант
( график функции у=х2+2х-3)
1. х0=-1, у0=-4
2. а=1, ветви
направлены вверх
3. Ось симметрии х=-1
4.
Х
0
1
2
у
-3
0
5

34.

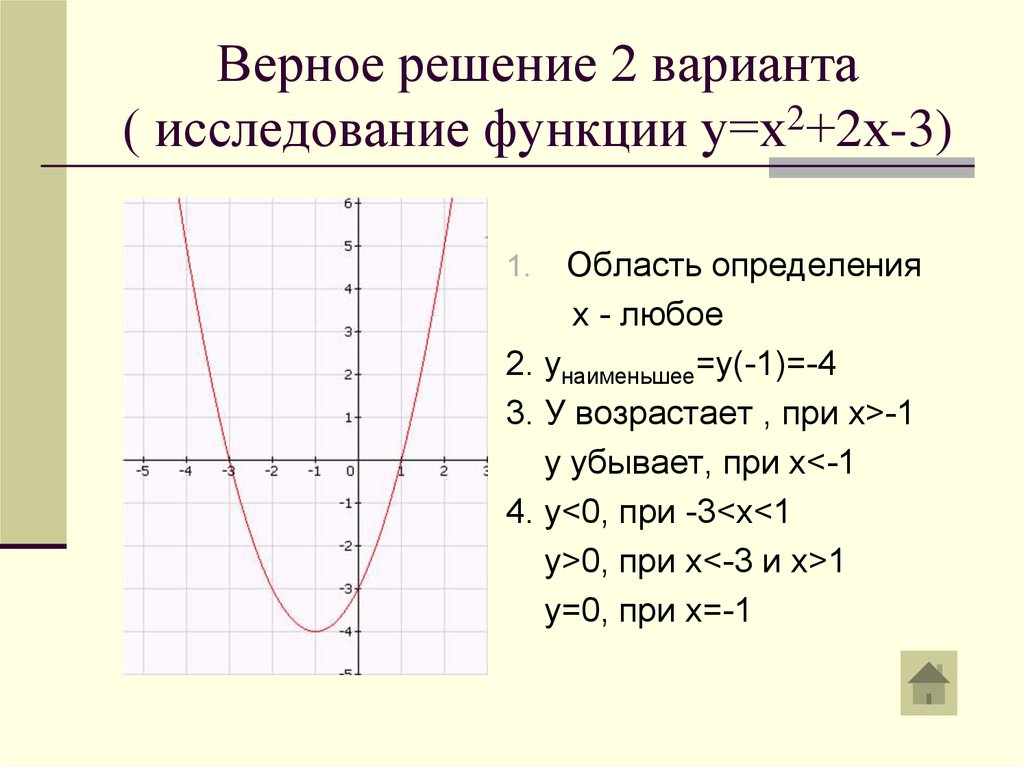
Верное решение 2 варианта
( исследование функции у=х2+2х-3)
Область определения
х - любое
2. унаименьшее=у(-1)=-4
3. У возрастает , при х>-1
y убывает, при х<-1
4. у<0, при -3<x<1
у>0, при х<-3 и х>1
у=0, при х=-1
1.