Симметрия в правильных многогранниках

1.

Муниципальное автономное образовательное учреждение
«Школа №47» г. Рязани
презентация по предмету : геометрия
«симметрия в правильных многогранниках»
работу подготовила
Ученица 10 «Г» класса
Пулатова О.М.
Проверила
Учитель геометрии
Кленьшина Н. В.
Рязань, 2024 г.

2.

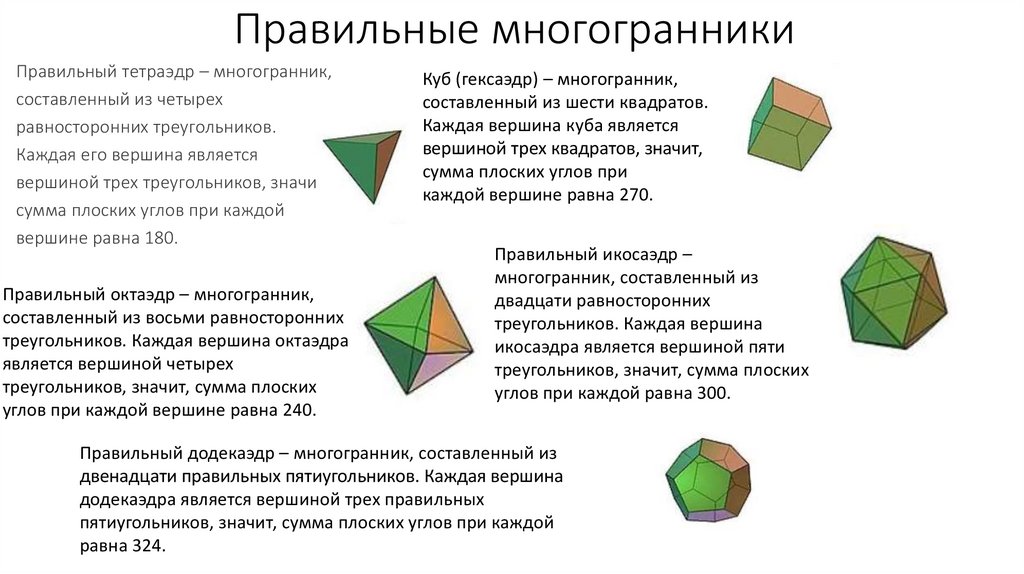
Правильные многогранники
Правильный тетраэдр – многогранник,
составленный из четырех
равносторонних треугольников.
Каждая его вершина является
вершиной трех треугольников, значит
сумма плоских углов при каждой
вершине равна 180.
Правильный октаэдр – многогранник,
составленный из восьми равносторонних
треугольников. Каждая вершина октаэдра
является вершиной четырех
треугольников, значит, сумма плоских
углов при каждой вершине равна 240.
Куб (гексаэдр) – многогранник,
составленный из шести квадратов.
Каждая вершина куба является
вершиной трех квадратов, значит,
сумма плоских углов при
каждой вершине равна 270.
Правильный икосаэдр –
многогранник, составленный из
двадцати равносторонних
треугольников. Каждая вершина
икосаэдра является вершиной пяти
треугольников, значит, сумма плоских
углов при каждой равна 300.
Правильный додекаэдр – многогранник, составленный из
двенадцати правильных пятиугольников. Каждая вершина
додекаэдра является вершиной трех правильных
пятиугольников, значит, сумма плоских углов при каждой
равна 324.

3.

Симметрия в пространстве и центрльнная
симметрия
Одно из интересных свойств правильных многогранников – это
элементы симметрии.Нам знакома симметрия из курса
планиметрии. Там мы рассматривали фигуры симметричные
относительно прямой и точки. В стереометрии же рассматривают
симметрию относительно точки, прямой и плоскости.Будем
говорить, что точки А и А1 симметричны относительно точки О
,если О – середина отрезка АА1. В таком случае О будет являться
центром симметрии и будет симметрична сама себе.
Точки А и А1 называются
симметричными относительно прямой
а, если прямая а проходит через
середину отрезка АА1 и
перпендикулярна к этом отрезку .
Прямая а называется осью симметрии,
а каждая ее точка считается
симметричной самой себе.

4.

Осевая и зеркальная симметрия
Точки АА1 называются симметричными относительно плоскости α, если плоскость α проходит через середину
отрезка АА1 и перпендикулярна к этому отрезку .Плоскость α называется плоскостью симметрии, а каждая ее
точка считается симметричной самой себе.Точка (прямая, плоскость) называется центром (осью, плоскостью)
симметрии фигуры, если каждая точка фигуры симметрична относительно нее некоторой точке той же
фигуры.Если фигура имеет центр (ось, плоскость) симметрии, то говорят, что она обладает центральной (осевой,
зеркальной) симметрией.

5.

Тетраэдр
У правильного тетраэдра нет центра симметрии.
Осью симметрии правильного тетраэдра является прямая, проходящая через середину двух противоположных ребер. То есть правильный
тетраэдр имеет три оси симметрии.
Плоскостью симметрии правильного тетраэдра будет плоскость, проходящая через ребро, перпендикулярно к противоположному ребру. То есть
правильный тетраэдр имеет шесть плоскостей симметрии.

6.

Куб
Центром симметрии куба является точка пересечения его диагоналей.
Осями симметрии будут прямые, которые проходят через центры противоположных граней или середины
противоположных ребер. Поскольку грани гексаэдра – квадраты, значит, оси симметрии будут проходить через
точки пересечения диагоналей противоположных граней. То есть у куба девять осей симметрии. Все оси симметрии
проходят через центр симметрии.

7.

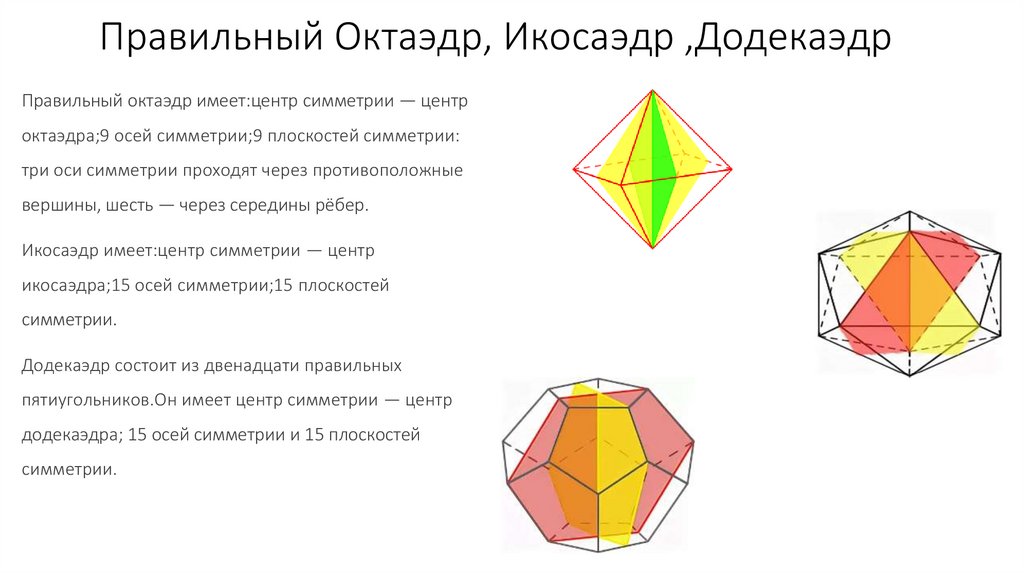
Правильный Октаэдр, Икосаэдр ,Додекаэдр
Правильный октаэдр имеет:центр симметрии — центр
октаэдра;9 осей симметрии;9 плоскостей симметрии:
три оси симметрии проходят через противоположные
вершины, шесть — через середины рёбер.
Икосаэдр имеет:центр симметрии — центр
икосаэдра;15 осей симметрии;15 плоскостей
симметрии.
Додекаэдр состоит из двенадцати правильных
пятиугольников.Он имеет центр симметрии — центр
додекаэдра; 15 осей симметрии и 15 плоскостей
симметрии.

8.

Задача
Какие из следующих утверждений верны?
1) Правильный шестиугольник имеет шесть осей
симметрии.
2) Прямая не имеет осей симметрии.
3) Правильный пятиугольник имеет пять осей
симметрии.
Если утверждений несколько, запишите их номера в
порядке возрастания

9.

Решение
Проверим каждое из утверждений.
1) «Правильный шестиугольник имеет шесть осей симметрии.»—
верно, при четном количестве углов оси симметрии проходят
через противоположные вершины и через середины
противоположных сторон.
2) «Прямая не имеет осей симметрии.» — неверно, прямая имеет
бесконечное число осей симметрии
3) «Правильный пятиугольник имеет пять осей симметрии.» —
верно, каждая ось симметрии любого правильного
многоугольника с нечетным числом сторон проходит через
вершину и середину противоположной стороны
Ответ: 13.